-
SuicideSuicidal folk can see it quite differently. Trust me. The problems are not "temporary" until their gone. Death is believed to provide that. — creativesoul
That is why there have never been atheist societies in history. They don't last long enough to make it into the history books. -
The essence of religion:roll: :sweat: — 180 Proof
The growth in the opioids crisis is exponential:
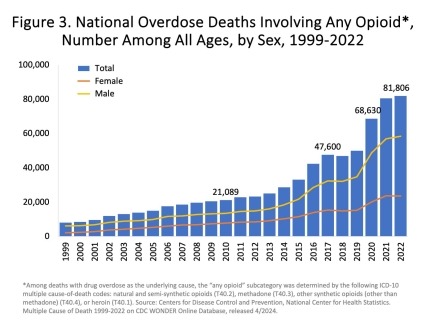
I think that we could make a mathematical model with input variable the number of people who believe in scientism and as output variable the staggered growth over time of people who rationally decide that there is no good reason for continuing the misery of their own lives.
In fact, the most interesting country to observe and predict would actually be China:
https://en.wikipedia.org/wiki/Irreligion_in_China
More recently, a 2015 Gallup poll found the number of convinced atheists in China to be 61%, with a further 29% saying that they are not religious compared to just 7% who are religious.
China is in the middle of a financial crisis that far exceeds the 2008 GFC in the West. According to internet rumors, 50% or more of the working-age Beijing population is unemployed now. Hundreds of millions of Chinese cannot pay their debts. The banks may or may not keep foreclosing on them. The problem is that the real estate being repossessed, left and right, is virtually worthless now.
Since the official communist propaganda is that fostering or even just having a bit of hope or similar spiritual values is not a legitimate scientific behavior and therefore just outdated bullshit, and since we can all agree that there is no rational reason for life itself, I am now watching with great interest how things are going to work out over there in "scientifically" atheist China. -
The essence of religionNo. If "existential ratiinalism", then there can be no "rational answer" for the existential nihilist. — 180 Proof
Look at this:
https://afsp.org/story/president-biden-reaffirms-commitment-to-mental-health-and-suicide-prevention
$602 million for the 988 Suicide and Crisis Lifeline, an increase of $100 million over enacted levels in FY 2023.
They spend over $600 millions per year on trying to give "hope", mostly to people who "scientifically" do not believe in hope.
If they believed in hope, they would have it already!
What a waste of money!
What an incorrigible bunch of idiots. -
The essence of religion. "Existential nihilism" is the choice to reject "rationalism" as a way of life — 180 Proof
Since there is no rational reason for the existence of life, existential nihilism is the rational answer.
Furthermore, since there is no valid rational reason to stay alive amidst difficulties and tribulations, there is no rational reason for suicide prevention either. There are only spiritual reasons, but these people reject them, because these reasons are not rational.
There is no rational reason for giving people hope. That is why suicide prevention does not work on 100% rationalists.
It is (rationally) outlandish to believe that things will get better for no reason at all. Hence, in rational terms, "hope" is just bullshit.
There is no salvation for a 100% rationalist.
Why do they even waste their time trying? -
The essence of religionFraming the line questioning as a reasonable one is faulty. The mistake is believing it is a rational question. — I like sushi
There is a scientific answer that should satisfy and will sedate the 100% rationalists, called "oxycontin". When I googled for the term, however, this is what Google showed on top of all search results:
Help is available
Speak with someone today
988 Suicide & Crisis Lifeline
For emotional and substance use support 24/7
Call 988
Text 988
So, the truly scientific answer to the question will instead be provided by the volunteer manning the 988 help desk.
But then again, the volunteer is trained to give spiritual answers instead of rational ones:
Learn how you can help move people from crisis to hope. We provide extensive training to qualified volunteers interested in staffing our Resource & Crisis Helpline or Youth Residential Programs.
So, in my impression, we will just keep running in circles.
They teach these volunteers to give people "hope", while these people want a scientific, rational answer to the meaning of existence! -
The essence of religionIt just appears to be reasonable to ask about a 'reason for existence'. — I like sushi
The question does not have a rational answer. That is not a problem for people who have a spiritual answer to the question but it is one for people who are 100% rational.
Since the existence of life is rationally meaningless, rationalism in this field always leads to existential nihilism. Motivation to keep going in spite of the inevitable difficulties will sooner or later start waning. This will eventually have to be medicated with antidepressants, anti-anxiety medication, and an ample supply of opioids and other painkillers. Since there is no rational reason to stay alive in such intolerable circumstances, the final solution is a complete abdication.
There is no hope for the ones who do not "believe" that there is. -
The essence of religionIf you are not being 'rational' then what are you being? — I like sushi
In this context, "rational" is the opposite of "spiritual". If we agree that there is no rational reason for the existence of life, rationalism will in this context always lead to existential nihilism. This is fine, until it isn't anymore. -
Mathematical truth is not orderly but highly chaoticTheories are not models and models are not theories. — TonesInDeepFreeze
The math exchange answer says something quite confusing in that regard:
To study "models", we need to work in a metatheory that already has some concept of set or collection. The "metatheory" here is the theory that we use, as a tool, to study the object theory. There are many options for such a metatheory. One option would be ZFC itself.
A model is not a metatheory, but "we need to work in" one "to study the model". So, as one of the options, we could "work in" ZFC itself to study its models.
I don't say that it is wrong. I just say that it is highly confusing. -
Mathematical truth is not orderly but highly chaoticBut to say that arithmetic can be reduced to logic requires showing, for example, the derivation of the axioms of PA from only logical axioms. And that ain't gonna happen. — TonesInDeepFreeze
You don't need the axioms of PA to carry out arithmetic. It will work perfectly fine without. You just won't have a theory about it. -
Mathematical truth is not orderly but highly chaoticI don't know your criteria for straightforwardness, but model theory is rigorously developed, though it does use infinitistic mathematics. — TonesInDeepFreeze
It works fine for me, as long as it talks about ZFC models of PA. Model theory also uses infinitistic mathematics in that context. I have no problem with that.
I only give up when it talks about the models of ZFC. At that point, it is no longer capable of cleanly separating provability and truth: "How can a model of ZFC be a set, if we want to use ZFC to study sets?"
Concerning "smoke and mirrors", well that is about models of ZFC, where the theory is essentially its own model. -
Mathematical truth is not orderly but highly chaoticWhat specific reduction do you have in mind? — TonesInDeepFreeze
"How Computers Work: Arithmetic With Gates"
http://www.goodmath.org/blog/2022/12/26/how-computers-work-arithmetic-with-gates
sum = x XOR y
carry = x AND y -
Mathematical truth is not orderly but highly chaoticLook at virtually any article or textbook to see that they are, modulo stylistic and symbol choices, along those lines and not with the existential quantifier in the scope of the turnstile. — TonesInDeepFreeze
Yes, I have noticed. But then again, I have never understood it like that. In fact, I have just always ignored it. I have always seen it as PA talking about itself.
Of course, some other theory could talk about PA, but the textbooks or papers do not seem to elaborate any examples. ZFC would not be a good candidate because it is too much like PA. ZF-inf is even bi-interpretable with PA. I have only ever run into one such example, i.e. Goodstein's theorem, where the theorem is in PA while the proof is in ZFC.
Moreover, when we move on to mention 'truth', the language for PA cannot be its own meta-language. — TonesInDeepFreeze
Yes, agreed. The truth of PA is in ZFC. But then again, where is the truth of ZFC? The only answer that I have found to this question is the following nebulous explanation on math exchange:
https://math.stackexchange.com/questions/1717893/in-relatively-simple-words-what-could-be-a-model-of-sf-zfc
My question is: What does a model of ZFC look like?
The question seems to come down to a common confusion: how can a model of ZFC be a set, if we want to use ZFC to study sets?
The answer is, essentially, that things don't work that way. To study "models", we need to work in a metatheory that already has some concept of set or collection. The "metatheory" here is the theory that we use, as a tool, to study the object theory.
There are many options for such a metatheory. One option would be ZFC itself, except that (by the second incompleteness theorem), ZFC can't prove that there is a model of ZFC.
In my impression, model theory is only straightforward for the simple case of PA being interpreted by ZFC's truth. Everything else seems to be smoke and mirrors. -
The essence of religionAnd anyway, as for pacifier, the same can be said about philosophical attempts to alleviate human suffering, from will to power, to communism, to transcendental subjectivity, to living in good faith. None of these approaches are apodictic. — ENOAH
Generational survival goes quite fast because life is rather short. We don't have time to figure out if something else is going to work than what worked for our parents. Seriously, if the solution does not work right away, the damage will be done already.
Nowadays, we have entire populations that refuse to have children and that increasingly even prefer to hedonistically overdose on all kinds of poisons. The antidepressant and anti-anxiety medication are not going to manage either, to indeterminately keep them in the rat race of life.
This epidemic of murderous rationality is highly contagious. People are much more likely to succumb if other people in their environment have succumbed already. Nihilism is highly infectious. It is like a virus. That is why social media such as Youtube and Tiktok strictly forbid videos on self-deletion. You can't even use the term. The vocabulary is simply banned.
The only strategy that people have time for, is to absorb whatever spiritual belief that worked for their parents, and then hope for the best. Otherwise, it is probably game over.
So, the approach does not need to be apodictic. It just needs to convince people away from -- in terms of rationality -- the meaninglessness of life. In other words, it does not need to be perfect. It just needs to be good enough. -
Mathematical truth is not orderly but highly chaoticIt is logic which proves arithmetic, not arithmetic itself. — Philosophim
Arithmetic can be reduced entirely to logic. However, logic can also be entirely reduced to arithmetic. You only need to do it for one universal gate NAND (or NOR) because all other logic can be implemented with it:
NAND(x,y) = 1 - (x*y)
Therefore, logic and arithmetic are perfectly bi-interpretable. If you can do the one, you can automatically also do the other. -
Pragmatism Without GoodnessMoral anti-realism is pretty common these days. It is arguably the dominant, "default" position. — Count Timothy von Icarus
Yes, because there is ultimately no rational reason for morality. In absence of an underlying non-rational spiritual reason, morality is simply nonsensical.
You can easily learn to extensively torture and mercilessly kill captives for the mafia. It is certainly a pragmatic choice because they pay you good money for doing that. If you can become an executioner for the official ruling mafia, and learn to enjoy your job, why not become one for an unofficial mafia? It even pays better. It has more perks and more fringe benefits. I don't see any "reason" not to do it. -
The essence of religionI am not keen on religious doctrines posing as a philosophy of consciousness, nor am I inclined to side with mysticism as anything other than a pacifier of sorts (albeit somewhat essential in its role on mental stability). — I like sushi
Since there is no rational reason for the existence of life itself, the absence of a pacifier may very well turn into a problem. Life can be full of suffering. When the going gets tough, why do you even try to continue? In order to perpetuate something that rationally does not make sense to begin with?
Rationality suggests that the answer is existential nihilism.
Surviving does not make sense while having children is simply cruel.
Without at least some spirituality that manages to transcend the nihilism of rationality, the rationalist cannot compete in the cutthroat environment of biological life. He simply won't find the motivation to do so. Hence, the rationalist needs lots of painkillers and other opioids to sedate his unsatisfied need for a reason to keep going, until he finally decides to put an end to his suffering by overdosing. -
Mathematical truth is not orderly but highly chaoticHe proposed the project. But he insisted that all of them undertake it? Moreover, is there even one colleague to whom Hilbert insisted the colleague undertake it? — TonesInDeepFreeze
David Hilbert had a habit of drawing the attention of the entire mathematical world to his agenda. He also successfully did that with his 23 problems:
https://en.wikipedia.org/wiki/Hilbert%27s_problems
Hilbert's problems are 23 problems in mathematics published by German mathematician David Hilbert in 1900. They were all unsolved at the time, and several proved to be very influential for 20th-century mathematics. Hilbert presented ten of the problems (1, 2, 6, 7, 8, 13, 16, 19, 21, and 22) at the Paris conference of the International Congress of Mathematicians, speaking on August 8 at the Sorbonne.
The other 21 problems have all received significant attention, and late into the 20th century work on these problems was still considered to be of the greatest importance.
Since 1900, mathematicians and mathematical organizations have announced problem lists but, with few exceptions, these have not had nearly as much influence nor generated as much work as Hilbert's problems.
Hilbert's list of 23 problems actually still had merit. There was no hidden agenda in them. His program, however, was about proving a falsehood, such as "mathematics is complete" (i.e. there is a proof for every truth). Hilbert wanted other mathematicians to find proof for his misguided ideology. -
Mathematical truth is not orderly but highly chaoticWhat untested vaccines? (Of course, they're untested for the people who are taking them in tests.) — TonesInDeepFreeze
These vaccines were obviously not tested for long-term consequences.
https://www.cancerresearchuk.org/about-cancer/find-a-clinical-trial/how-clinical-trials-are-planned-and-organised/how-long-it-takes-for-a-new-drug-to-go-through-clinical-trials
Drug testing and licensing
All new drugs and treatments have to be thoroughly tested before they are licensed and available for patients.
A new drug is first studied in the laboratory. If it looks promising, it is carefully studied in people. It may be then licensed if the trial shows that it works well and doesn’t cause too many side effects. You may hear this process called ‘from bench to bedside’.
There is no typical length of time it takes for a drug to be tested and approved. It might take 10 to 15 years or more to complete all 3 phases of clinical trials before the licensing stage. But this time span varies a lot.
There are many factors that affect how long it takes for a drug to be licensed.
If the habitual length of time it takes, is 10 to 15 years, to test a new drug for long-term consequences, then I do not want to use a drug that was tested for at most 6 months. -
Mathematical truth is not orderly but highly chaoticSo the existence statement is in the meta-theory, not in PA. — TonesInDeepFreeze
So, according to your remark, the diagonal lemma should be phrased as:
∃ A ( PA ⊢ ( A ⇔ ¬Bew(ÍAÎ ) ) )
instead of :
PA ⊢ ∃ A ( A ⇔ ¬Bew(ÍAÎ ) )
This is an extremely subtle difference because A still needs to be phrased in the language of PA. Therefore, A must also be a sentence in PA.
Another problem is that PA is its own meta-theory in this case. That is the whole point of encoding ÍAÎ as a natural number. We thereby make use of the fact that PA is capable of self-reflection.
If PA is not its own meta-theory in this case, what theory is then the meta-theory? -
Can the existence of God be proved?You still don't realise that it has been proven that Gödel's version of the proof is inconsistent. — Lionino
For a starters, the alleged inconsistency detected by Christoph Benzmüller and Bruno Woltzenlogel-Paleo cannot be duplicated with automated provers. Secondly, Melvin Fitting's reformulation addresses this concern anyway.
You are merely haphazardly copying excerpts from the ongoing investigation and conversation on Gödel's proof.
Of course, there are concerns about the nitty-gritty details in the proof. You are desperately fishing for evidence that there would be something wrong with Gödel's work without being a constructive participant in any shape, way, or fashion.
The people that you quote mention possible concerns with a view on improving the original and making progress, while you are sitting on the fence, overhearing fragments of their conversation, with only negativity and foregone conclusions in mind. If you were physically present in the meeting room, they would tell you to leave the room because you are not adding any value with your non-constructive negativity. -
SuicideThere are people with these symptoms who are spiritual. Ergo, It's not a spiritual problem — Moliere
Empirical studies suggest otherwise:
https://ajp.psychiatryonline.org/doi/10.1176/appi.ajp.2011.11091407
In this issue, Miller and colleagues present data from a longitudinal study of offspring from a sample of depressed and nondepressed subjects to determine if religion or spirituality influenced the onset and course of major depression over the 10 years of follow-up (1). They found, among individuals who affiliated as either Protestant or Catholic, that subjects who reported religion or spirituality as highly important were 76% less likely to experience an episode of major depression during the follow-up. In contrast, religious attendance and denomination had no impact. The protective effect was experienced primarily among subjects at high risk because their parents experienced depression.
But then again, I agree that the only truly rational solution to the problem is medication. -
SuicideIf you've decided to end your life, for either a rational or emotional reason, that's hardly a handicap. — Vera Mont
Some people plead for mercy to the spiritual overlord while others abuse antidepressant and anti-anxiety medication. By the way, there is also no opioids overdose crisis in countries where people prefer the spiritual route:
https://www.health.state.mn.us/communities/opioids/prevention/painperception.html
The United States makes up 4.4% of the world’s population, and consumes over 80% of the world’s opioids.
Antidepressants, anti-anxiety medication, and opioids are the rational solution to a spiritual problem. There simply is no rational reason for life itself. Therefore, the only truly rational solution for the rational meaninglessness of life is to medicate it away.
It is not just that the unbelievers do not want children. They are even actively self-deleting. In the meanwhile, we pray to the spiritual Lord, and carry on, with or without the unbelievers. -
Suicide
Since your identity is closely tied to the ultimate reason why you are motivated to stay alive, no matter how hard that sometimes may be, and since there is simply no rational reason for life itself, tying your identity to rationality is in fact a threat to your survival.That sums you up nicely. Thanks. — Vera Mont -
Suicidethat's right, islamic doctrine is philosophically lifeless — flannel jesus
So is the grass, the birds, and the trees. -
Suicidegood thing Islam isn't replying to me in this forum then — flannel jesus
Abstractions don't reply, I guess. Why would an abstraction do that anyway? It is not even alive to begin with. -
SuicideI really could not care less what Islamic doctrine says — flannel jesus
And vice versa. It doesn't care either what you think about it. Hence, the relationship is reciprocally perfectly sound. -
SuicideYah. I think that comes under the religious, rather the rational heading. — Vera Mont
I use rationality merely as a tool. I actually only use it when it suits me and I certainly do not identify with it. There may possibly be rational reasons to have hope and to keep faith in the future in spite of all adversity, in spite of all tribulations, but why use a hammer when the better tool is actually a screwdriver?
There are no rational reasons why life itself exists. So, why would there be a rational reason for insisting on staying alive and surviving in spite of all the hardships? When the going gets tough, the most straightforward solution is to seek out a crash course in spirituality and then use it to overcome your difficulties in life.
I personally do not believe that rationality can stimulate your survival instinct. In my opinion, it is simply of no use in that context. -
SuicideInescapable suffering that makes any joy in life impossible seems like a valid reason to me. — flannel jesus
According to Islamic doctrine, no suffering is inescapable. There is always hope.
Quran 4:30 And kill not yourselves. Surely, Allah is Merciful to you.
Patience is a virtue. Allah promises great rewards for those who bear hardship with patience.
If you have strong capacity to believe, then you can make use of such capacity to faith to believe that things will eventually get better and to sit out the temporary misery. That is the power of religious autosuggestion. -
Mathematical truth is not orderly but highly chaoticNot I, but Langendoen and Postal. If you wish you can take up the argument, I'm not wed to it, I'll not defend it here. I've only cited it to show that the case is not so closed as might be supposed from the Yanofsky piece. — Banno
Langendoen and Postal argue in "The vastness of natural languages", 1984, that natural-language sentences can be infinitely long.
https://aclanthology.org/J89-1006.pdf
This book is an extended argument in support of the theses that natural languages are transfinitely unbounded collections, that sentences are not limited in length (number of words) by any cardinal number, finite or transfinite, and that no constructive grammar can be an adequate grammar for any natural language.
https://fa.ewi.tudelft.nl/~hart/37/publications/the_papers/on_vastness.pdf
However, as I mentioned before, the authors do not so much argue for “not assuming a size law” but for “assuming the negation of a size law”. For example, the rules (if any) of English do not stipulate a maximum finite length of sentences; one can easily break such a stipulation by prefixing a maximum length sentence with “I know that”. The rules of English also do not explicitly state that sentences should be finite; one can add “All English sentence should be finite in length” to the rules or not. The authors argue, quite vociferously at times, against adding that condition mostly on the grounds that it is not a purely linguistic one. However, and this is where I disagree, they then conclude that, somehow, necessarily there should be sentences of infinite length.
Yanofsky, on the other hand, assumes that language sentences, especially predicate formulas that describe natural-number subset properties in ZFC, are necessarily finite.
Even though infinitary logics allows for infinitely long predicate formulas, they cannot be represented in language but only by their parse trees:
https://en.wikipedia.org/wiki/First-order_logic
Infinitary logic allows infinitely long sentences. For example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables. Infinitely long sentences arise in areas of mathematics including topology and model theory.
Infinitary logic generalizes first-order logic to allow formulas of infinite length. The most common way in which formulas can become infinite is through infinite conjunctions and disjunctions. However, it is also possible to admit generalized signatures in which function and relation symbols are allowed to have infinite arities, or in which quantifiers can bind infinitely many variables. Because an infinite formula cannot be represented by a finite string, it is necessary to choose some other representation of formulas; the usual representation in this context is a tree. Thus, formulas are, essentially, identified with their parse trees, rather than with the strings being parsed.
Hence, the size of logic statements represented by language alone cannot be infinite. Therefore, the language of ZFC is still countably infinite.
Overcoming this constraint would require the use of meta-programs instead of predicates as set membership functions that have infinite while loops -- beyond primitive recursive arithmetic (PRA). These programs can then generate infinitely long predicates in the language of ZFC to describe Yanofsky's subsets. The use of such predicate-generating meta-programs instead of predicates as set membership functions is not supported in the language of ZFC.
Furthermore, this would still not help, because there are only countably infinite programs. There would still not be enough programs to describe all the uncountably infinite subsets of the natural numbers. -
Mathematical truth is not orderly but highly chaoticBut the point is that "...the collection of all properties that can be expressed or described by language is only countably infinite because there is only a countably infinite collection of expressions" appears misguided, and at the least needs a better argument.
Your posts sometimes take maths just a little further than it can defensibly go. — Banno
The lemma that the number of possible expressions in language is countably finite is actually a core argument in Yanofsky's paper:
http://www.sci.brooklyn.cuny.edu/~noson/True%20but%20Unprovable.pdf
Another important uncountably infinite set is the collection of subsets of the natural numbers. The collection of all such subsets is uncountably infinite. Now that we have these different notions of infinity in our toolbox, let us apply them to our concept of true but unprovable statements. All language is countably infinite. The set of statements in basic arithmetic, the subset of true statements, and the subset of provable statements are all countably infinite.
This brings to light an amazing limitation of the power of language. The collection of all subsets of natural numbers is uncountably infinite while the set of expressions describing subsets of natural numbers is countably infinite. This means that the vast, vast majority of subsets of natural numbers cannot be expressed by language. The above examples of subsets of natural numbers are expressed by language, but they are part of the few rather than the many. The majority of the subsets are inexpressible. They defy language.
There is simple proof for the lemma that language is countably finite. Yanofsky's paper does not mention it but the proof is trivial:
https://math.stackexchange.com/questions/1206460/proving-that-the-set-of-all-english-words-is-countble
This is the question : Prove that the set of all the words in the English language is countable (the set's cardinality is אo) A word is defined as a finite sequence of letters in the English language.
Answer 1: There are 26 letters in the English language. Consider each letter as one of the digits on base 27. This mapping yields that the cardinality of your set is ≤|N|, hence this set is countable.
Answer 2: The set Sn of the English words with length n is finite (this is almost obvious). So it's also countable. Why is it finite? The set An of all sequences with length n made up of latin characters is finite as it contains 26n elements. Only some of these sequences are meaningful/actual English words. So Sn⊂An. So Sn is also finite. The set T for which you have to prove that it is countable is: T=S1∪S2∪S3∪... Now you have this theorem: "A countable union of countable sets is also countable". Applying it you get that T is also countable. Thus your statement has been proved. -
Flies, Fly-bottles, and PhilosophyBut the whole point Wittgenstein's argument on the autonomy of mathematics systems is that a mathematical proposition is internally tied to its proof/proof system — Richard B
Wittgenstein's view is not compatible with model theory of which the core understanding is that the provability of a arithmetical proposition is tied to one system (PA) while its truth is tied to another system (ZFC).
https://en.wikipedia.org/wiki/Model_theory
In mathematical logic, model theory is the study of the relationship between formal theories (a collection of sentences in a formal language expressing statements about a mathematical structure), and their models (those structures in which the statements of the theory hold).
The model-theoretical approach is necessary in order to discover that there exists arithmetical truth in ZFC that is not tied to a proof in PA. Wittgenstein subscribes to a syntactic notion of truth. Model theory subscribes to the semantic nature of truth.
In fact, Wittgenstein does not properly distinguish between provability and truth.
If dealing with autonomous calculi then no matter how similar the rules of the two systems might be, as long as they differ - as long as we are dealing with distinct mathematical systems - It make no sense to speak of the same proposition occurring in each. The most that can be concluded is that parallel propositions occur in the two systems which can easily be mapped onto each other. — Richard B
Wittgenstein simply rejects the essence of model theory, because mapping propositions in PA to propositions in ZFC is exactly what model theory does. It is exactly about "the same proposition occurring in each".
Hence Godel was barred by virtue of the logical grammar of mathematical proposition from claiming that he had constructed identical versions of the same mathematical proposition in two different systems. — Richard B
In their seminal paper "On interpretations of arithmetic and set theory" of 2006, Richard Kaye and Tin Lok Wong formally proved that PA and ZF-inf are indeed bi-interpretable and therefore that the mapping in model theory -- in and of itself -- does not entail any of the risks that Wittgenstein incorrectly believes to exist.
Bi-interpretability:
- Every logic sentence in PA can be mapped to an equivalent logic sentence in ZF-inf. (Von Neumann)
- Every logic sentence in ZF-inf can be mapped to an equivalent logic sentence in PA. (Ackermann)
https://web.mat.bham.ac.uk/R.W.Kaye/publ/papers/finitesettheory/finitesettheory.pdf
The work described in this article starts with a piece of mathematical ‘folklore’ that is
‘well known’ but for which we know no satisfactory reference.
Folklore Result. The first-order theories Peano arithmetic and ZF set theory with the
axiom of infinity negated are equivalent, in the sense that each is interpretable in the
other and the interpretations are inverse to each other.
Perhaps the first and most obvious conclusion is that statements concerning the equiv-
alence of ‘Peano Arithmetic’ and ‘ZF with the axiom of infinity negated’ require some
care to formulate and prove. It is certainly true that PA and ‘ZF with the axiom of infin-
ity negated’ are equiconsistent for just about any sensible axiomatisation of the latter,
in the sense that interpretations exist in both directions.6 Probably this is the ‘folklore
result’ that most people remember. But for the finer result with interpretations inverse
to each other, careful axiomatisation of the set theory is required. A category theoretic
framework for interpretations is useful to direct attention to these refinements.
It is true that until 2006, model theory had always assumed the bi-interpretability of PA and ZF-inf without formal proof or similar investigation. Gödel never formally proved this mapping either. It was rather being considered self-evident. It would actually have been valid criticism to point out that Gödel assumed bi-interpretability without proof. For Wittgenstein to outright reject bi-interpretability, however, was clearly one bridge too far. -
You build the machine, or you use the machine, because otherwise you are trying to be the machineWhy have you got it in for the math professors? — Tarskian
I don't. I also have no problems with bank staff. They are just pawns. They are just trying to make a living. -
You build the machine, or you use the machine, because otherwise you are trying to be the machineBut why hate on the math professors? — fishfry
I don't hate on individual math professors. They are just pawns in the game.
One (or rather two) of the things I don't like, is the combo of academic credentialism combined with the student debt scam. Like all usury, it is a tool to enslave people. The banks conjure fiat money out of thin air and them want it back along with interest from teenagers who were lied to and most of whom will never have the ability to pay back. The ruling mafia even guarantees to the bankstering mafia that they will pay in lieu of the student, if he ultimately doesn't. First of all, though, they will exhaust all options afforded by the use of violent threats of lawfare. -
Mathematical truth is not orderly but highly chaoticThese are all mathematical truths, but they're not very interesting mathematical truths. — fishfry
Agreed. Unpredictable truths in the physical universe are usually not particularly interesting either. The difference is that we can see them or at least observe them. That is why we know that the physical universe is mostly unpredictable. Our own eyes tell us. In order to "see" a mathematical truths, however, we need some written predicate. Otherwise, such truth is invisible to us.
If we completely ignore the unpredictable truths in the physical universe, it also gives us the impression of being beautifully and even majestically orderly. In that perception of the physical universe, there is no chaos. In that case, the physical universe also looks like a beautiful sculpture.
leaving only the beautiful sculpture that is modern mathematics — fishfry
Yes, and that is absolutely not the problem.
The problem is that people such as David Hilbert are convinced that the beautiful sculpture is all there is. Hilbert insisted on the idea that his colleagues had to work overtime in order to give him proof of his false belief:
https://en.wikipedia.org/wiki/Hilbert%27s_program
Statement of Hilbert's program
The main goal of Hilbert's program was to provide secure foundations for all mathematics.
Completeness: a proof that all true mathematical statements can be proved in the formalism.
Decidability: there should be an algorithm for deciding the truth or falsity of any mathematical statement.
...
Kurt Gödel showed that most of the goals of Hilbert's program were impossible to achieve.
The vast majority of people still see mathematical truth like Hilbert did. They still see mathematical truth as a predictable and harmonious orchestra of violins.
Out of the uncountably infinite and random universe of mathematical truth
Yes, you seem to know it perfectly fine. Most people, however, don't know it, simply because they don't want to know it.
They believe that one day we will discover the fundamental knowledge to see the entire physical universe also as a beautiful sculpture. We have already discovered the fundamental knowledge of arithmetic. Its axioms are known already and arithmetical truth is absolutely not a beautiful sculpture. Instead, it is uncountably infinite and random. -
Mathematical truth is not orderly but highly chaoticRight, and despite their work being concluded for quite some time now, people several times smarter than both you and I combined still hold math and science as tools of precision and meaningful discovery. — Philosophim
If you feel threatened by its chaotic nature, it means that it disturbs your ideological beliefs. Someone who really uses them as tools of precision and meaningful discovery would never feel threatened by that.
I find this point more interesting. Why? — Philosophim
It is probably best to use an example from the Soviet Union but in fact modern western society does exactly the same:
https://www.marxists.org/subject/marxmyths/john-holloway/article.htm
In speaking of Marxism as ‘scientific’, Engels means that it is based on an understanding of social development that is just as exact as the scientific understanding of natural development. For Engels, the claim that Marxism is scientific is a claim that it has understood the laws of motion of society. This understanding is based on two key elements: ‘These two great discoveries, the materialistic conception of history and the revelation of the secret of capitalistic production through surplus-value, we owe to Marx. With these two discoveries Socialism becomes a science. The claim that Marxism is scientific is taken to mean that subjective struggle (the struggle of socialists today) finds support in the objective movement of history. The notion of Marxism as scientific socialism has two aspects. In Engels’ account there is a double objectivity. Marxism is objective, certain, ‘scientific’ knowledge of an objective, inevitable process. Marxism is understood as scientific in the sense that it has understood correctly the laws of motion of a historical process taking place independently of men’s will. All that is left for Marxists to do is to fill in the details, to apply the scientific understanding of history. The attraction of the conception of Marxism as a scientifically objective theory of revolution for those who were dedicating their lives to struggle against capitalism is obvious. At the same time, however, both aspects of the concept of scientific socialism (objective knowledge, objective process) pose enormous problems for the development of Marxism as a theory of struggle.
It is very convincing, because it sounds scientific, and because it insists that it is scientific, and especially because you will get burned at the Pfizer antivaxxer stake if you refuse to memorize this sacred fragment from the scripture of scientific truth for your scientific gender studies exam.
As you can see, everybody who craves credibility insists on sailing under the flag of scientism and redirect the worship and adulation of the masses for the omnipotent powers of science to themselves and their narrative. -
Mathematical truth is not orderly but highly chaoticAgain, hyperbole. I can assure you if we were able to predict how everything in the universe worked — Philosophim
The complete and perfect theory of everything cannot do that. It won't be able to predict everything. It would improve our ability to predict the physical universe from 0.1% to 0.3% of the true facts. So, it will possibly triple the predictive power of physics but not more than that.
We already have the theory of everything for the natural numbers, which is PA. It does not help us to predict the vast majority of mathematical truths. Most of the truth about the natural numbers is still unpredictable.
No, nothing you have discovered here has shaken the foundations of math or science. — Philosophim
I did not discover anything. Gödel certainly did. Chaitin also did. Yanofsky moderately did. I just mentioned their work.
What method did you use to find out that its true? — Philosophim
It is an opinion and not a theorem. There is nothing wrong with mathematics or with science. My problem is with positivism and scientism. I find these ideological beliefs to be very dangerous. -
The essence of religionThe case for a higher authority, an absolute authority, has to be argued philosophically. Not religiously, that is, not according anything so instantly assailable. — Constance
Well, Christianity is indeed collapsing. Ever more rapidly.
Christianity has indeed turned out to be assailable but certainly not easily or instantly. It took centuries until the French Revolution for its assailants to finally make a dent. The other religions are still doing fine. I think that it has become clear that it is not possible to dislodge them. It is not possible to convince a traditional Jew out of Judaism or a traditional Muslim out of Islam.
We just don't have time to figure out alternative solutions to religion. If you don't have something handy that works right now, and that already has a track history of success, then you are going to be too late to still make a difference. Life moves on. Life is also short. I cannot wait for a solution to fall out of the skies. In fact, it has already fallen out of the sky. So, why not just use it? -
Mathematical truth is not orderly but highly chaoticIt sounds as though you yourself hold some rather specific and rigid beliefs that likewise are not entirely objective in their genesis. — Pantagruel
Well, yeah, I rigidly believe that we should not give powers to people that only Allah should have, and if Allah does even not exist, then so much the better. -
Mathematical truth is not orderly but highly chaoticJust like I wouldn't grab a wrench if I were studying the atomic level of the universe, one shouldn't use certain language and terms when dealing with the foundations of knowledge and mathematics. — Philosophim
The true nature of the universe of mathematical facts makes lots of people uncomfortable.
Imagine that we had a copy of the theory of everything?
It would allow us to mathematically prove things about the physical universe. It would be the best possible knowledge that we could have about the physical universe. We would finally have found the holy grail of science.
What would the impact be?
Well, instead of being able to predict just 0.1% of the facts in the physical universe, this would improve to something like 0.3%; and not much more.
Scientism is widespread as an ideology in the modern world. Any true understanding of the nature of mathematical truth deals a devastating blow to people who subscribe to it. This is exactly why I like this subject so much.
The hyperbole just isn't true. — Philosophim
That is wishful thinking.
You may not want it to be true, but it is.
In 1931, Gödel's incompleteness theorems dealt a major blow to positivism and scientism, but it was just the beginning. It is only going to keep getting worse. As Yanovsky writes in his paper:
Gödel’s famous incompleteness theorem showed us that there is a statement in basic arithmetic that is true but can never be proven with basic arithmetic. That is just the beginning of the story.
In my opinion, scientism needs to get attacked and destroyed because its narrative is not just arrogant but fundamentally evil. It is a dangerously false pagan belief that misleads its followers into accepting untested experimental vaccine shots from the lying and scamming representatives of the pharmaceutical mafia; and that is just one of the many examples of why all of this is not hyperbole.
Tarskian

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum