How do you define this measure in pure mathematical terms? You cannot use probability, because probability is physics (unless you find a sound mathematical definition of probability) — Mephist

https://en.wikipedia.org/wiki/Measure_(mathematics)

Measure theory is an abstraction of the concept of length, area, volume, etc; and also of probability. In fact probability theory is based on measure theory.

In fact if you know the Kolmogorov axioms of probability, that's basically measure theory.

A measure is a function from the collection of subsets of a given set, to the nonnegative real numbers satisfying some conditions. If in addition the measure of the entire set is 1, that's a probability measure.

The measure of the rationals in the reals is zero. And in fact the measure of any countable set must be zero. This follows from countable additivity. The measure of all computable bitstrings has measure zero for the same reason. That means if you pick a real number "at random," the probability is zero that you'll pick a computable real.

Will someday be falsified', is not the same as 'has been falsified'. The falsification is what determines the faults, demonstrating the weaknesses of the theory, showing us where improvement is needed. There is no point in dismissing theories which have not yet been falsified, because we would not know what needs to be improved. That's the scientific method, observations which are inconsistent with what the theory predicts reveal the faults in the theory. But until those inconsistent observations come about, we don't know where the weaknesses of the theory lie. — Metaphysician Undercover

Which has what to do with what we were talking about, the use of symbols to represent things we don't understand?

If you cannot see that the truth of this statement indicates that the theories have been falsified, then I'm afraid your denial is beyond hope. — Metaphysician Undercover

Name me a theory of science that hasn't been falsified or will not someday be falsified. You're a scientific nihilist. You deny the entire enterprise because it doesn't serve up absolute truth on a platter.

But instead of facing this fact, that the theories are wrong, someone has dreamed up a name "dark matter", and they attribute the fact that the theories are wrong to this mysterious thing, "dark matter". Why not just call it like it is, "the theories are wrong", dump the theories, and the "dark matter" which the theories necessitate because they're wrong, and get on with producing a new theory which doesn't make this mistake? — Metaphysician Undercover

I hope you'll forgive me but I prefer not to engage with your scientific nihilism, which itself is driven by scientific ignorance. If we threw out everything we don't understand, we'd have never understood gravity or electromagnetism. You simply know and understand nothing about the things you're talking about.

Well, if the universe had no beginning then the past is infinite. So here we have the past as negative infinity as that's what you mean using the integers. Now consider the now to be any number on the integer number line: -3567, -9, 0, 1, 2019, etc. How do we reach these points? We'd have to pass through a positive infinity of time to reach these points. Now, is that possible? Of course not. Why? Think of the positive infinity {0, 1, 2, 3,...}. Can we pass through this positive infinity of time to reach any point that can be considered the present? Impossible, right? There has to be a beginning. It's not turtles all the way down. — TheMadFool

$- \infty$ is not a point on the number line.

For just a moment, forget that we're talking about time or causality. Just consider the number line of integers:

.., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...

Nobody complains about it. It goes on infinitely in both directions, but there are no endpoints, Nobody ever says, "Well there MUST be a finite endpoint on the left but not on the right.

Nobody ever says, "How could -4 exist? We'd already need -5 to exist. Etc. And the process could never start."

Nobody ever says that. We take for granted that the integers go right and left forever.

In particular there is no leftmost point that you need to "start from" in order to "reach" -4. Rather, -4 is right there. -4384378437 is there. Every integer is "just there."

Why isn't it possible that time or causality are like that? Just because you have an intuition of a first element doesn't make your intuition right. As was noted recently, Buddhists have a very different intuition about the flow of time. You are simply expressing a Western cultural tradition. "In the beginning God created the heavens and the earth." That's essentially why you have such a strong psychological conviction that there must be a "first element."

After all you are not arguing that we could never reach 5 "from the right." Why not? Past and future are symmetrical. Think of the block universe model of physics.

To "reach -4 you start at ANY integer, and either move right or left a finite number of steps. There are no points at plus or minus infinity.

Bottom line you're simply repeating your Western beliefs. But why can't time be eternal in both directions? Why can't it be circular? Who says it can't be these things?

One way to define "constructive physics" is simply to say, "it uses constructive mathematics". But definitions of the latter sometimes arise principally from avoiding the LEM. Another tack is to avoid non-computable numbers. Or simply to state that experiments must be conclusive in a reasonable finite amount of time. I'm not sure what you two are referring to here. But I haven't read all the thread. — jgill

Right. Constructive physics is physics based on constructive math. That's all it is. Instead of using the real numbers, you only use computable numbers. Or something.

You cannot test if it is countable or not with physical experiments limited in time (how do you know that you don't get the same results again after a — Mephist

Why are you trying to convince me that math isn't physics? I'm talking about the measure of computable bitstrings in the space of all bitstrings. The measure of the computable bitstrings is zero.

Constructive physics (constructivist logic) can ASSUME the existence of a function that you can call "random" (whatever it means: it's an axiomatic theory), representing a physical process. Only that you cannot DERIVE or COMPUTE this function. You have to assume it as an axiom of the theory. The point is that this is allowed by the logic because you cannot introduce inconsistencies in this way! — Mephist

My understanding is that the constructivists allow in nonconstructivity whenever they paint themselves into a corner. For example every type of constructivism includes some form of the axiom of choice, because you can't do math without it. Arguably you can't even do physics without it. There's a weak form of choice needed to prove the Hahn-Banach theorem, a key theorem in functional analysis; which, as I've mentioned, is the mathematical framework of QM. Whether you can do QM without any form of choice I do not know. But the constructivists aren't as pure as they claim to be. And in the end they'll be proven wrong about the world. That's my opinion, but it may take centuries for me to be right.

i — Mephist

you cannot count on the fact that you always get the same output for the same input with absolute certainty: you get results that are statistically determined, but not deterministic. — Mephist

“No man ever steps in the same river twice, for it’s not the same river and he’s not the same man”, said Heraclitus in 544bc.

But you asked, "What if there exists no such thing in nature?" But that is not a problem for math, because math is not physics. In math there is certainty about the repeatability of functions.

I like the idea of a Boltzmann brain. The universe is completely random. Like static on a tv set. Once in a while, by perfectly random chance, a region of the universe suddenly coheres into a conscious mind. That's me. Or all of us. We'll be blinking out in an instant or two.

The idea that the universe is repeatable, or orderly, or understandable, etc., is a philosophical assumption. You can do science without making that assumption but most scientists prefer to believe their work is "about" something. I'm sure the bloodletters and proponents of the phlogiston theory of heat felt the same way in their time.

(fishfry: how did you post that graph? Are you a forum subscriber?) — jgill

In the Edit window there's a row of icons with B for bold, slanted I for italic, etc. The eighth icon from the left lets you insert a graphic from the Web.

There are two major zeros, and two minor zeros, to account for postive/negative and negative/positive.

One zero implies a positive bias, so I'd agree with TheMadFool. — Qwex

You don't take my point about Poughkeepsie?

Hindus or Buddhists certainly wouldn't. — Wayfarer

That's a good point. The first-mover argument is essentially a Christian idea. "In the beginning God created the heavens and the earth." That's @Devans99's argument and William Lane Craig's as well. The intuition comes from one's cultural upbringing. Westerners have a hard time imagining forever in both directions. But they are willing to accept forever in one direction as long as it's to the right. Where is the logic in that??

It's not valid to write ... -> -5 as '...' is undefined then -5 is also undefined. — Devans99

Ellipses simply means the pattern continues. How would you write the set of integers? Just like that.

You are confusing your evidence-free intuitions with a rational argument.

Anything existing in time forever is impossible. It would have no initial state so no subsequent states — Devans99

If you state that as a premise, then you are assuming what you want to prove.

If you want to believe that time or the universe must necessarily have a beginning, you are free to make that assumption.

I am suggesting that it is logically coherent to make the opposite assumption, and I offer the totally ordered set of integers as a thought-model or analogy.

If you argue against me by simply restating your assumption, that's not an argument.

Why couldn't the universe have simply existed forever? Or for that matter why couldn't it go forward in time a long ways, then loop back to the past, a circular model of time. Take the unit circle in the plane as a model of time. You just keep going 'round and 'round and there's no beginning and no end.

What makes you so sure your model is correct, except for a vague feeling that there must be a first cause. Well then that first cause existed forever. You can't escape this problem by saying God did it.

That's not an example at all. We know a lot about dark matter, that's why we can name it. — Metaphysician Undercover

You just make this shit up. How do you measure how much we need to know about something before we can name it? On the contrary, the day they discovered that the galaxies are spinning too fast to hold together, they named the cause "dark matter" while having no idea what it is or whether it exists at all.

In fact I already made that point to you. Read my post again.

Similarly fishfry has his own speculative narrative built up from his interpretation of the facts (and for some reason is even more inordinately sure of himself). — Baden

I'd have gladly stuck around for intelligent dialog; but once I was told to "step off" it was either tell that individual to FUCK off, or depart the conversation. It's not that I don't know how to be a rude asshole; I just prefer not to interact with people who choose that mode of communication. And if they flip out every time someone goes slightly off-topic in an online discussion thread, they must flip out alot. But in this case I don't think that was the problem. I think I triggered that individual's delicate political sensibilities and they didn't have the wit to engage on the topic of the psychodynamics of male-female relationships. As I say you could study Jungian archetypes or Berne's "Games People Play" or the collected works of Sigmund Freud to find this Royal couple described as the ancient archetypes and scripts they are acting out.

I actually noted that by calling my remarks "sexist" and reaching for the smelling salts, that poster demonstrated how people these days are brainwashed by political ideology to the point that they have no interest at all in human nature. But I gave some classic authors on the subject, you could go read their books and look them up and thereby gain much insight into your own behavior. People don't look inward anymore, they like to make everything political.

So, genuine concern over a genuine issue or poking the market for profit? Mixed bag at best. — Baden

I stated my opinion and I stand by it. But I have no concern, I'm not actually a follower of the Royals. I only pay attention when the latest scandal is so ubiquitous in the news that I can't avoid it. I'm interested in the psychodynamics of the relationship, but I don't care one way or another about them as people.

You know why Americans love the Royals? We get to enjoy the pomp, the circumstance, and the salacious scandals, and we don't have to pay for it. That honor belongs to the British people.

But if you are asking if I sometimes like to poke the politically correct, well of course, it's great sport.

I did say "either that or there must be, at least, two kind/types of zeros" Are you implying -0 is not the same as +0? — TheMadFool

They're exactly the same. So there aren't two types, only one type. Because there's only one zero.

I have an answer to your latest post about the infinite regress but I'm too tired to write it up. Will respond to that tomorrow.

This is the graph of $f(x) = \frac{1}{x}$. If you write $y = f(x)$ then it comes out to your notation using $y$. Another way it's often written is $xy = 1$. The graph is a pair of hyperbolas, one in the first quadrant representing all the positive solutions, and one in the third quadrant representing the negative solutions.

You'll note that as $x$ approaches zero from the right, $y$ goes to $\infty$. And as $x$ goes to zero from the left, $y$ goes to $- \infty$. This explains what you're seeing. But there aren't two kinds of zeros or one kind of infinity in this context. That part of your logic isn't clear. You're deliberately choosing a pair of points: One is along the positive x-axis, and the other is on the negative y-axis. So you're "riding two different trains" going in opposite directions. Your pairs have one point on each of the hyperbolas. I don't see how you derive your conclusions. They don't seem to follow from what I understand of your argument.

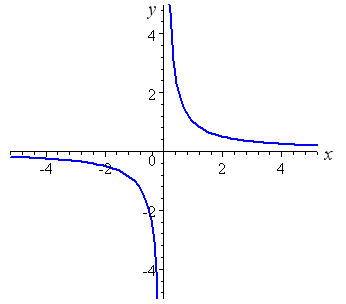
However notice the pattern. as x approaches positive infinity, 1/x approaches Zero from the positive side AND as y approaches negative infinity, 1/y approaches Zero from the negative side. — TheMadFool

This is entirely correct as you can see from the diagram.

Note that negative/positive of zero is zero i.e. -0 = +0 = 0. — TheMadFool

This part doesn't make sense. It doesn't follow from the previous sentence.

Consider: If I travel to Poughkeepsie from the east; or I travel to Poughkeepsie from the west; in either case I end up at Poughkeepsie.

Likewise if I approach zero from above; or I approach zero from below; either way the limit is zero.

In fact what's going on is that as x goes to +infinity, f(x) goes to zero on the x-axis.

As y goes to -infinity, y goes to zero from the negative side on the y-axis.

Somehow you're conflating all this into erroneous conclusions.

Short answer: for a finite experiment, "a priori" probabilities are simply functions that count the total number of possible results, "assuming" that each result has the same "probability" (yes, that's a circular definition: no formal definition of what "probability" is, even using ZFC set theory). — Mephist

You can certainly define a measure on the unit interval of reals and assign probabilities to sets of bitstrings. I didn't follow this post. You said you can't define probabilities for bitstrings but you can.

No, in QM the pattern is NOT computable: the pattern is NOT predictable from the theory, so you DON'T NEED any computable function to predict it! — Mephist

Confused by this. Constructive physics wouldn't allow a random sequence.

Yes, EXACTLY! — Mephist

Ok. So whether we use constructive or classical real numbers, we get the same physics. We get the same theorems and we can't measure any difference.

However, we do not necessarily have the same metaphysics. The world may be classical or constructive. It may consist only of computable things or it may contain noncomputable things. Our theories can't tell the difference and our experiments can't tell the difference. But ultimate reality may in fact be one or the other, computable or not. Which supports my belief that noncomputability is the next frontier in physics. If someone ever proves that a noncomputable real is necessary to explain some observable physical phenomenon, it's off to the races to find such a thing in the world. I'm talking a hundred years down the road, maybe longer.

It's impossible for it to be, as you say, turtles all the way down because we're at a particular position in the sequence, right? There must be an ordinal number, as in nth number, that marks our position in the sequence. What is that number? There is none as I illustrated with the various ways the set of integers Z can be written. — TheMadFool

Not at all. What law of nature says the collection of causes must be well-ordered? I agree it's intuitively appealing that there must be a first cause; but that's not a proof. Let me give you an example. The integers mark the years according to the Western calendar. We're currently at 2020. Ok, we're here. No question about it. And there was a year before that and a year before that, going back forever.

This is difficult intuitively; but there's no principle of nature that says it can't be so. And after all, God is not a principle of nature either. People who deny the possibility of infinite regress are reasoning with their emotions, not with logic.

Another way to look at it would be that every number in the sequence of integers corresponds to the ordinal number infinity itself; — TheMadFool

The set of integers is not well-ordered so you can't claim that. It's false. You want to try to make $- \omega$, so to speak, your "first element." But that is not the model. The model has no first element. It's like Peano in reverse. Every integer has an immediate predecessor as well as an immediate successor. Again, it's only your intuition that's objecting. You haven't got an actual argument. You can't. How do you know the universe isn't an infinite regress of causes?

after all we can only reach it after "beginning" at negative infinity by completing an infinite number of steps. It's my humble opinion that the infinite regress technique basically relies on the inability to complete an supertask as this is; to "begin" at negative infinity and reach any finite position in the sequence is impossible. — TheMadFool

No. You are trying to reach an integer from the "beginning" on the left. You can't do that in the integers. You surely know that. There was no beginning. There was no first cause. How do you personally know that the universe isn't like that? There is no negative infinity in this model. There's no negative infinity in the integers.

Do you have this same complaint about the number line itself Of course you don't. It would never cross your mind. Start at zero and you can always move a unit to the right or a unit to the left.

And why is it that you can always move a unit to the right but not to the left? My model has nicer symmetry. You have no fundamental explanation as to why you can move forever in one direction but hit a wall if you go too far in the other. You're making that up. You have a feeling but not a logical argument.

For a contemporary theory, if only a speculative one, consider Roger Penrose's cyclic universe. He posits an endless cycle of big bangs and big crunches. Who's to say he's wrong? There doesn't need to be a first cause. It IS turtles all the way down.

She's following a classic toxic female script.
— fishfry

What is that and why is this perspective not sexist? — frank

Labeling my remark sexist is not an argument against my point. I do apologize if you feel that I hijacked your thread. This isn't the time for me to explain toxic femininity to you; nor the concept of psychological scripts and unconscious motivations, and the male and female archetypes. I'd suggest you start with some Freud, some Eric Berne, some Jung perhaps.

I'll step off right here, thanks.

I didn't realize the question would be hi-jacked in this way. — frank

I did not knowingly hijack. A lot of people are saying two things right now:

1) That Meghan was treated badly by the Royals due to her race. On the contrary, she was welcomed with open arms, given a boatload of money to renovate her free new house, welcomed at all family events, etc.

2) That people who criticize Meghen are racist. That is also not true. She's following a classic toxic female script.

If you post a video without actually making your point in the accompanying text, you can't be surprised that not every response will meet your expectations. I asked you if you'd summarize the video for me and I reiterate the request.

Discuss the issue raised in the OP or step off, ok? — frank

I don't watch videos. Text is faster. Can you summarize it please? It says it's about racism. I don't think there's a racial angle to this. The Royal family welcomed the hell out of her. People are trying to make this bitch into a victim.

Can you change your sex? I think so. — Bartricks

Why is Caitlyn Jenner celebrated and Rachel Dolezal excoriated? 'Splain me that. It's a puzzler.

Bullpucky. Nobody (not me anyway) gives a shit about Meg's heritage. She's a toxic female running and ruining the life of a weak male. That cuts across races. People want to make Meg-hate a racial thing but it's not. She's isolating him from his friends and family. Isn't that a classic sign of an abuser? Her own brother warned Harry not to marry this, ah, rhymes with witch. Broken relationship with her dad, totally self absorbed, loves living the lifestyle of the rich and famous. Marries into the Royal family then says, "It's not working for me."

My God is this all too complicated for people to see?

It's toxic femininity. Not racism.

I didn't answer to this yet, so I'll do it now.

In general, category theory can be used to represent formal logic systems and their interpretations, in the obvious way: an interpretation is a functor from a category representing the language to a category representing the model ( https://en.wikipedia.org/wiki/Categorical_logic ). — Mephist

I think what I was getting at is that you made the claim that constructive and classical physics were equivalent categories; and I asked you to clarify how you were categorifying physics. I don't think you answered but it's not an important point. I would certainly take on faith that what you say is true.

Actually what you've convinced me of so far is that constructive math and standard math give the same theory of physics; since in QM we are only doing computable calculations anyway. Is that right?

I was just a little unclear about which category you're using. I know Baez and others use category theory in physics, but I don't know if there are official categories that describe gravity or QM or whatever. Doesn't really matter. Your main point is that constructive math is just as good as classical, since we only use computable calculations. And you are being agnostic about whether the actual universe is constructive or not. Is that a fair summary of your view?

The vectors of this Hilbert space are the wave functions (not observable).
Observables are represented by Hermitian operators on the Hilbert space.
And the results of experiments (the numbers corresponding to the measured quantities) are the eigenvalues o these Hermitian operators.
(P.S. it's impossible to understand how it works from this description, but that's the way it is, if you want to be mathematically accurate) — Mephist

As it happens, here is how I learned about what you're describing. I never had much physics background. A few years ago I had the opportunity to seriously study some functional analysis. Functional analysis is basically infinite-dimensional linear algebra combined with calculus, if you think of it that way. Normed vector spaces, Banach spaces, Hilbert spaces. For example you can recover the subject of Fourier series as a particular example of an orthonormal basis. One day I discovered that the mysterious bra-ket notation, which was something I thought I'd never be able to understand in this lifetime, turns out to be nothing more than a linear functional operating on a vector, written in inner-product notation. At that moment I realized I understood a lot of QM without having to study physics. So I actually understand all of what you said, from a mathematical point of view.

And now that you mention it ... that's one of my arguments against constructive physics! A Hilbert space is a complete inner product space. By complete we mean Cauchy-complete. So you can't even have such an object in constructive math, because the constructive real line is not Cauchy-complete.

Now if I'm understanding some of your comments correctly, you are saying this doesn't matter because even if we assume the constructive real line, we can still prove the same theorems. Constructive completeness is just as good as completeness, for purposes of calculations in QM. And even if there is ultimately a difference, we couldn't measure that difference anyway!

Perfectly sensible. We could do physics with the rational numbers and a handful of irrational constants if we needed to. No experiment could distinguish that theory from a theory based on real numbers.

This is a very interesting point I hadn't considered before. It makes the enterprise of constructive physics seem somewhat more reasonable to me. Am I understanding you correctly?

No, I didn't say you can calculate anything. You can calculate the magnetic moment of the electron in quantum electrodynamic with arbitrary precision, but only in theory (because the number of operations necessary grows exponentially with the number of calculated decimals), — Mephist

Wrong theory. If something is computable or not, that's computability theory. If something is computable efficiently or inefficiently, that's complexity theory. You're conflating the two. Minor point but you've done it twice so I thought I'd clarify this point.

You can calculate the magnetic moment of the electron. Period. The efficiency of the calculation is a separate topic and has nothing to do with whether it's computable. I suspect you know that but forgot to make that distinction as you were typing.

But I don't know why you keep mentioning this. You can't measure the prediction with arbitrary accuracy in the real world. We're agreed on this point.

But I wanted to point out that there are parts of QM that are in some sense "mathematically perfect". Meaning: there are a finite set of atoms corresponding to all the possible combinations of electrons' orbitals up to a certain number of electrons (82 stable elements? I don't remember). And that ones are "perfect shapes", in the sense that two of them of the same type are exactly the same shape, like two squares. Usually (before QM) physics was made of objects that only corresponded to mathematical objects in an approximate way (orbits of planets for example), but if you looked carefully enough, every object in the physical world was different, and different from the mathematical object that represented it.
Atoms, and particles in QM in general, are different: they are "digital" (quantized) and not "analogical" shapes. So, in some sense, they are "perfect" (mathematical?) objects. — Mephist

Ok. Not exactly sure what you're saying here. I've already stipulated long ago that I know that all electrons are identical. That is in fact a highly strange phenomenon. You pointed out to me that atoms can be identical to other atoms. That's interesting. This last para I didn't quite follow.

It doesn't make sense that you would have assigned the symbol "2" to something and you know absolutely nothing about this thing which you have assigned the symbol to. — Metaphysician Undercover

Here's a nice contemporary example of exactly that.

Do you happen to know what dark matter is? Don't worry if you don't, because nobody knows what dark matter is. It's a name given to something we can not understand but wish to study.

The story goes like this. Astronomers can estimate the amount of matter in a given galaxy. We can also measure the galaxy's rotational speed. It turns out that most galaxies are spinning so fast that they don't have enough matter to hold them together gravitationally. By all our known theories of physics, galaxies should have flown apart long ago. Why didn't they?

We have no idea. Being human, a creature with the power of abstraction (you must have not gotten your share) we give it a name even though we have no idea what it is or what it might be.

Dark matter is the name given to some hypothetical "stuff" that interacts with the gravitational field but no other fields. By contrast, a rock falls to earth so it interacts with the gravitational field. And you can see it, so it interacts with the electromagnetic field. That's normal for the stuff we call "stuff."

Dark matter must therefore be something that's matter, in the sense that it interacts gravitationally; but it's dark. It doesn't interact with electromagnetism. You can't see it. In fact "dark" is the wrong name, it should be transparent matter. But dark matter is the name that stuck.

So, is there dark matter? Maybe. We just don't know what it is yet.

Or maybe there is no dark matter at all. Perhaps the law of gravity needs to be tweaked so that at galactic distances, it has a little extra pulling power to hold the galaxies together. This fascinating idea is called Modified Newtonian Dynamics, or MOND.

"Dark matter" is therefore a symbolic phrase to stand for something that causes some effect, but we have no idea what it is, or even if it exists. Yet we reason about it and write scientific papers about it.

That's scientific abstraction. You know nothing of science. I'm impressed. The more I get to know you, the wider your sphere of ignorance seems to become.

So probably you mean the bitstreams that contain an infinite amount of information (not obtainable as the output of a finite program). There is no way to prove that such strings exist using a formal logic system (even using ZFC): — Mephist

Nonsense. I can prove it easily. The measure of the unit interval is 1; the measure of the computable reals in the unit interval is zero. Therefore there must be a whole lot of of noncomputable reals in the unit interval.

You're claiming that if I flip infinitely many coins, they must land in a pattern that is computable. That's clearly nonsense. How would the coins know to do that? On the contrary, it's incredibly unlikely that an infinite bitstring is computable and "almost certain," as they say in measure theory, that it's not.

OK I'll stop arguing about intuitionism. But I think you didn't get my point here, so let me try one last time: — Mephist

For two people trying to end a conversation we're not doing a very good job.

I want to make a semantic point, which is that intuitionism is too vague. It's way more than constructivism. Intuition in Brouwer's formulation has a mystical component that I can never make sense of. I use the term neo-intuitionism to stand for all the contemporary attempts to revive the idea, minus the mysticism: constructive math, homotopy type theory, etc.

Cantor's theorem is valid in intuitionistic logic, but we know that intuitionistic real numbers are countable. In fact the theorem says: forall countable lists, there is an element that is not in the list, and we know that the set of elements missing from the list is countable because the list of all strings is countable.
Now you read the same theorem in ZFC and you interpret it as "there is an uncountable set of elements missing from the list". How do you know that the set of missing elements is uncountable? I mean: the symbolic expression of the theorem is the same, and the interpretation of the symbols is the same. How can you express the term "an uncountable set" in a language containing only the quantifiers "forall" and "there exists one" ?
And if there is no uncountable set of missing real numbers, there are no holes to fill.. — Mephist

But there are. It's a theorem that a Cauchy-complete totally ordered field must be uncountable. The constructivists pretend all the noncomputable numbers don't exist. But that's nonsense. Chaitin's constant exists (as a real number) and it's not computable. The Halting problem is not computable. Lots and lots of naturally occurring phenomena are noncomputable. Newtonian gravity is noncomputable. (The jury's still out on QM). You can't close your eyes to things then say they're not there. There's more to mathematical truth than proving theorems, as Gödel demonstrated. You can prove that the constructive real line is "computably complete," but it's still not complete, as in the example of truncations of Chaitin's constant shows.

For the first part of the question, I guess your question is how do you say "a finite random sequence" in intuitionistic logic. You can't! (at the same way as you can't do it in ZFC: the axiom of choice does not say "random" function). If the sequence is finite it is always computable, so you can say "there exist a finite sequence of numbers" ( the same as in ZFC ).
There is a definition of randomness as "a sequence that is not generated by a program shorter than the sequence itself" (lots of details missing, but you can find it on the web), but this is about the information content and not about the process used to choose the elements of the sequence.
About the bitstrings that aren't computable: all finite bitstrings are computable of course. So probably you mean the bitstreams that contain an infinite amount of information (not obtainable as the output of a finite program). There is no way to prove that such strings exist using a formal logic system (even using ZFC): we can interpret the meaning of Cantor's theorem in that way, and maybe there is such a thing in nature, but you cannot prove it with a finite deterministic formal logic system. — Mephist

You seem a little off topic here. I asked you what principle of nature, or math for that matter, forces a sequence of coin flips to be computable. Of course I agree that any finite sequence of flips is computable, we can compress it just by writing down its base 10 equivalent. But if you flip infinitely many coins. you will get a computable sequence with probability zero. How can constructivists hope to get so lucky?

All infinite causal regresses are impossible — Devans99

I just showed you a model of infinite causal regress. It's the plain old integers. What law of nature says it can't exist? On the contrary, it probably does exist. What caused the big bang? Random quantum fluctuations in the vacuum state of the pre-universe. What caused that? What caused the laws of physics? What caused that cause? You never get to the bottom.

It seems to me that "There can't be an infinite regress therefore God" is a terrible argument. How do you know there can't be an infinite regress? The integers are a model of infinite regress.

Z = {...-3, -2, -1, 0, 1, 2, 3,...} or Z = {...-4, -3, -2, -1, 0, 1, 2, 3, 4,..} or Z = {...-2, -1, 0, 1, 2,..} — TheMadFool

These notations designate the same ordered set.

The point is that there's no reason that there must be a first element in an ordered set of causes. The first-mover argument assumes what it's trying to prove. How do you know there's not an infinite regress of causes? "It's turtles all the way down."

Using the infinity of integers doesn't succeed in solving the problem that there is no first fine-tuner. — TheMadFool

Why not? To me it seems like this is the solution to the first mover problem. Everyone's moved yet there is no first mover.

What law of nature says that movers or tuners must be modeled by the natural numbers but not the integers?

I want to know what the symbols are being used for. If you assert that the symbol "2" represents an object, I want a clear description of that object, so that I can recognize it when I apprehend it, and use the symbol correctly. — Metaphysician Undercover

You reject science. In science we DON'T know what something is. So we give it a symbolic name, write down the symbol's properties, and reason about it in order to learn about nature.

When Newton wrote $F = ma$ those were made up terms. Nobody knew (or knows!) exactly what force or mass is. Acceleration's not hard to define. But even then Newton had to invent calculus to define acceleration as the second derivative of the position function.

You reject all that.

Nihilism.

Pascal's Wager is relevant because you have to decide to believe something because if you don't, you're screwed. — Carolyn Young

I think there's a bit of a logic flaw in Pascal's wager. You have to not only believe in God, you have to believe in a God that condemns you to eternal hell or promotes you to eternal heaven, based on whether you've been bad or good. In effect, God is conflated with Santa Claus. "He knows when you've been bad or good so be good for goodness sake" is an expression of Pascal's wager!

An infinite regress of fine tuner’s is impossible* — Devans99

Why not? What if each fine tuner (fine tuna?) is indexed by an integer, like so:

$\dots, -4, \ -3, \ -2, \ -1, \ 0, \ 1, \ 2, \ 3, \ 4, \ 5, \dots$

Each tuner tunes the tuner directly to their right. So -4 tunes -3; -3 tunes -2; and so forth.

You will note that every tuner is tuned; and that there is no untuned tuner

You and William Lane Craig should meditate on this model.

But, hey! We got the Super Bowl and Twinkies, right? — Noah Te Stroete

The federal government requires television networks to beam free NFL football games into my living room in HD. That's the kind of authoritarianism I can get behind.

Algebra makes the same mistake as set theory, assuming that a symbol represents an object. — Metaphysician Undercover

Alright man. It's not set theory you object to, it's 10th grade algebra. It's not abstraction you object to, it's the very concept of using the symbol '2'.

I simply can't argue with such a nihilistic position. You claim that one must know and understand the referent of a symbol before being allowed to use that symbol. That flies in the face of the entire history of science. And nobody likes flies in their face. I bid you adieu.

I believe humans lack the capacity to organize any significant conspiracy that wouldn’t result in their jailing or demise. People have consciences, differing wants, motives, and fears, that any cabal is doomed from the outset. — NOS4A2

This is a common claim of people trying to debunk conspiracy theories. I have four points of refutation that have been on my mind. I'm so glad we're talking about conspiracy theories. I love conspiracy theories.

Now, the claim is that "All those people couldn't keep a secret." I disagree.

1) Consider the Manhattan project to build the atom bomb in WWII. 130,000 people worked at 32 separate locations for three years and nobody breathed a peep. There was one German spy and he got caught. So a very large group of people CAN keep a secret, if the reason for secrecy is good enough.

2) The fact that secrets usually leak out is a kind of survivor bias for secrets. The only secrets you know are the ones that leaked. You don't know all the secrets you don't know. The things the CIA and FBI and other alphabet soup agencies do in your name that you don't know about are highly numerous and mostly evil. You don't know about them because people DO keep secrets.

3) Not everybody needs to know. The 1977 movie Capricorn One, is about a US mission to Mars that is faked by the government. Only a few people know about the plot. The workers in Mission Control are fed fake tapes. They think they're getting the live data.

So even if a thousand people are involved, only a handful at the top might actually know what's really going on; and the rest have no idea they're participating in a nefarious activity.

4) Who says you have to keep secrets? Say you have 1000 people in a room, and you are the Evil Leader of their terrible plot. You COULD say to them, "If any of you talk, you'll be in big trouble." Guaranteed that at least a few of them will get their story to Wikileaks or equivalent. Your plot will be on the front page of the New York Times by morning, even if just to call Wikileaks liars.

So no, that doesn't work. What do you do instead? You say to them: When the plot is complete, I want you all to go out and tell every wild story you can think of to the press! Some of you can even tell them the truth. Use my name! Tell the truth. Tell lies. Sow confusion!

Isn't that much more effective? And doesn't it fit the pattern? Take the JFK assassination. Is the problem that nobody's talking? No, it's that everybody's talking. You have so many people out there putting forth alternative theories that the average American doesn't bother to listen to any of it. There's a guy named James Files who has actually confessed to being one of the grassy knoll shooters. Nobody believes him!

So that's what you do. You don't keep secrets. You sow confusion. Look at 9/11. Dozens of alternative theories, all of them conflicting with each other. Planted explosives. Thermite. Micro-nukes. Reports of explosions in the basement. Real planes. CGI-projected fake planes. Missiles disguised as planes. Cheney did it. Mossad did it. The Saudis did it. No plane wreckage was every recovered at Shanksville. Yes there was! No there wasn't! The alternative literature on 9/11 is huge. Buried in there somewhere is the truth. But you can't separate it from the lies. The average person sees all this confusion and goes, "Well they're all nuts. What the government told me must be right."

The "Nobody can keep a secret" theory stands refuted.