-
Continuum does not existOk. You are disconnecting Q at a point that does not exist in Q. Thought you were restricting all points to Q. Usual approach to this is to assume the underlying reals. — jgill
Am I misunderstanding you? The rationals are not connected in the subspace topology because you can partition them into two disjoint open sets: those rationals whose squares are less than 2, and those whose squares are greater than 2. Didn't mention any irrationals. -
Continuum does not existYes, usually it is inherited from the usual topology on the reals. But ignoring the non-reals seems OK. Looks like it is connected as well. But not a linear continuum since it doesn't have the LUB property. Rusty here I"m afraid. — jgill
Can't be connected. The two sets and are both open (proof in a moment) and disconnect .
In other words I'm disconnecting at .
Why are and open?
I noted earlier that the intervals with are a base for the topology. To see that is open, we write for all such that . The proof that is open is analogous.
Of course I see that I have to include the unbounded intervals and in my base. (ps -- I don't need to, that's just a notational convenience).
ps --
Ah now I'm the rusty one. All of the intervals (p,q) are open in the subspace topology of the rationals relative to the reals. So I didn't need all this machinery, my sets A and B are already open in the subspace topology. -
Continuum does not existIf I'm not mistaken, no non-empty set of rationals is open in the reals. — TonesInDeepFreeze
Right, that was the point of my question to @sime. I did convince myself that if you take the rationals by themselves, you can define a topology by all the "open" intervals (p,q) with p and q rational. That would be a base for a topology on the rationals I believe. Not 100% sure but I think it's likely. If you define the open sets as all the finite intersections and arbitrary unions, you'd have a topology. That might be what sime means. Can't think of any other interpretation of an open set of rationals, since no nonempty set of rationals is open in the subspace topology of the reals as you note.
So then my next question was, given that topology on the rationals, how does sime propose to construct the reals. I suspect that in the end he'd have to reinvent Dedekind cuts. -
Continuum does not existIn my case, i am stressing the benefits of a "top down" approach, in which one uses lattice theory to define a lattice of abstract elements that is isomorphic to the open sets of the rationals extended by end points. — sime
It's well known that the powerset of any set forms a distributive lattice.
"The power set of a set, when ordered by inclusion, is always a complete atomic Boolean algebra, and every complete atomic Boolean algebra arises as the lattice of all subsets of some set. "
https://en.wikipedia.org/wiki/Power_set
From there, can you walk me through your idea of how to use this to construct a model of the reals that satisfies the least upper bound property? -
Continuum does not existI meant L and R to refer to open sets of rationals — sime
Can you give an example of an open set of rationals? You've used the term several times. With respect to the usual topology on the reals, the rationals are not open nor are the intersections of the rationals with open sets of reals. So I'm a little confused on your meaning of an open set of rationals.
ps -- If you already had the reals, you could define open sets of rationals in terms of the subspace topology. But since we are trying to construct the reals, I'm not sure if that works. Perhaps you can define a topology on the rationals as being generated by open intervals of rationals. That might work. Is that what you intend? -
Continuum does not existI'm saying that if L| R is a Dedekind cut consisting of two open sets — sime
I believe you should review the definition of Dedekind cuts. First, they can't be open sets, since (as Tones pointed out) L and R are sets of rationals.
then the union of L, L|R and R is a disjoint partition of the continuum, — sime
That's not true either, since L and R are sets of rationals. I'm repeating myself, but you keep making the same error. And there IS no continuum (within set theory) until we have the set of ALL Dedekind cuts, not just a single one.
But you are making a larger conceptual error. We already know what the real numbers are. The real numbers "form the unique (up to an isomorphism) Dedekind-complete ordered field."
https://en.wikipedia.org/wiki/Real_number
That axiomatic definition is sufficient to satisfy philosophical notions of the continuum, as well as derive all other properties of the reals. Once you have an ordered field with the least upper bound property, you couldn't ask for anything more in terms of a continuum.
The purpose of Dedekind cuts is so that if someone says, "Oh yeah? How do we know there even IS such a thing?" we can show them the construction and say, "We can construct such an object within set theory." So we show them the construction once (or work through it in real analysis class once in our lives) and never think about it again. From now on we only need the axiomatic properties, having convinced ourselves that we could always construct such an object within set theory if challenged.
It's analogous to defining 0, 1, 2, 3, ... as 0 = {}, 1 = {0}, 2 = {0,1}, etc. As Benacerraf noted, since there are infinitely many possible encodings of the natural numbers within set theory, none of them can actually "be" the natural numbers. Rather, this particular construction demonstrates that if challenged, we could construct a model of the Peano axioms within set theory.
The moral of the story is that we should not conflate the set-theoretic construction of a thing, with the thing itself, which is generally defined axiomatically by its characterizing properties. -
Continuum does not existZen masters wrote with one hand while erasing with the other — Gregory
And then there was the left-handed Zen master who erased his words before he wrote them. -
Continuum does not existwhen i pressed fishfry on Zeno, he said uh oh let's not discuss it. — Gregory
Because it's miscategorized in this thread, not for any other reason. There's a lengthy and tedious supertask thread that was active a few weeks ago that I do not want to see reactivated here. That's what I was referring to.
Why would you attribute sentiments to me out of context like that?
You don't want me to start attributing you out of context, do you?
ps -- When you mentioned Zeno to me I responded on point here.
https://thephilosophyforum.com/discussion/comment/932896 -
Continuum does not existI thought fishfry was referencing the set of all sets and numbers, — Gregory
Cantor's absolute infinity was the collection of all ordinal numbers, which he called an "inconsistent multiplicity," since he recognized that the collection of all ordinals could not be an ordinal.
A quick web search turned up this interesting looking article. "Cantor, God, And
Inconsistent Multiplicities"
https://intapi.sciendo.com/pdf/10.1515/slgr-2016-0008
such AI bots are so often horribly wrong and fabricate regularly — TonesInDeepFreeze
Not unlike certain posters I could name! :rofl: :rofl: :rofl: :rofl: :rofl: :rofl: -
Continuum does not existDid not Godel and Cantor believe that once one sees Absolute Infinity he knows all (the whole story of mathematics)? — Gregory
Cantor thought the absolute infinity was God. I don't know if he ever claimed it was the whole story of mathematics.
Don't recall reading whether Gödel had an opinion on the matter. I don't think the concept of absolute infinity was relevant by Gödel's time. -
Continuum does not existI am genuinely baffled why so often in this forum you get me completely backwards. — TonesInDeepFreeze
Leads to some spirited and entertaining conversations. -
Continuum does not existGiven that I already have a definition of 'the limit', I can just say 'the limit' without reciting again its definiens. — TonesInDeepFreeze
This is what I'm confused about with your objection to the extended reals (or integers, etc.)
I noted that the extended reals are essentially a notational convenience, and we could live without them.
And you seemed to be arguing that because we COULD live without them, then we SHOULD live without them.
That's the part I don't understand. The definition of limit is rather involved, at least for people first encountering it, involving epsilon and delta and universal and existential quantifiers and so forth.
By your logic (as I understand it), it would be parsimonious (a virtue, I gather, but I'm not sure why) to dispense with it, and do the raw epsilonics every time we want to mention a limit.
So that's what I'm genuinely confused about (no trolling, no jokes). You object to the use of the extended reals as a notational convenience for infinite limits and limits at infinity; but you do NOT likewise object to the use of the word "limit" as a notational shortcut for the epsilonic definition of a limit. Nor do you want me to further break that down by defining absolute values and the < sign.
I don't understand your point about the extended reals. They're a definition that makes expressing some mathematical ideas simpler, exactly like "limit" or "<" or "12" for "xxxxxxxxxxxx".
Why do you approve of some notational conveniences and not others? After all, ALL definitions are notational conveniences and could in principle be dispensed with in favor of writing out their meanings until we have nothing but primitive logical symbols. That would be maximally parsimonious yet also maximally incomprehensible. The whole point of definitions is to help people "chunk" their understanding of complex concepts. That's exactly what the extended reals do. They let us express infinite limits and limits at infinity in a compact notation. -
Continuum does not existI don't get it. Or maybe adducing that quote is just your way of saying "yeah yeah" ironically. If so, whatever. — TonesInDeepFreeze
At this point I'm just trolling you. You're sometimes an easy target because you take yourself so seriously; and I was born a wiseass and can't help myself.
Whoa. I did not at all invoke unrestricted comprehension. — TonesInDeepFreeze
Heck you didn't. You, or somebody using your keyboard (do you have a cat perchance?) wrote:
I understand the idea that given a property, there is the set of things that have that property (with some restrictions on that principle). — TonesInDeepFreeze
My emphasis in boldface.
That is unrestricted comprehension or my name's not Gottlob Frege. You wrote "with some restrictions," but the required restriction, namely restricted comprehension, would entirely negate your point. -
Continuum does not existbut also hope that some reasonable liberty is granted — TonesInDeepFreeze
Was it not perfectly clear the other day that the usual order on the integers carries over to the extended integers? Where was your reasonable liberty then? Your concept of reasonable liberty only goes one way.
But today you were flat out wrong to claim that "reason" shows that there are infinite sets. That's an inaccuracy which no amount of reasonable liberty can fix. Likewise your invocation of unrestricted comprehension to justify that claim. I couldn't find any reasonable liberty there so I corrected your material errors. It's a full time job, let me tell you. -
Continuum does not existI don't know the relevance you intend with that quote. — TonesInDeepFreeze
"My point was to contrast informal deduction with "mind's eye" visualization." -
Continuum does not exist(1) Rejecting the axiom of infinity does not entail that there are no infinite sets. Rather, both rejecting the axiom of infinity and adopting the negation of the axiom of infinity entails that there are no infinite sets. (This pertains to ZF.) — TonesInDeepFreeze
"During a lecture, the Oxford linguistic philosopher J. L. Austin made the claim that although a double negative in English implies a positive meaning, there is no language in which a double positive implies a negative. Morgenbesser responded in a dismissive tone, "Yeah, yeah.""
https://en.wikiquote.org/wiki/Sidney_Morgenbesser -
Continuum does not existI should have counted on someone not recognizing that my remarks are merely in the spirit of personal reflection. — TonesInDeepFreeze
"When caught in a material error, I just claim I didn't really mean it that way."
Too tedious to likewise mock and debunk every single point you made in this post. I stand by my previous remarks. You made multiple substantive errors, which I corrected. You are the one who attacks every little technical inaccuracy anyone makes, even if their overall meaning is obvious. But you don't hold yourself to that same standard. -
Continuum does not existThanks for the clarification. Can we calculate the contribution of the ω
�
th term to the series? — MoK
It's not any term of the sequence. It's the LIMIT of the sequence. I know you took calculus a long time ago. They taught you that 0 is the LIMIT of the sequence 1/2, 1/4, 1/8, 1/16, ..., correct?
0 is not ANY TERM of the sequence. It's the LIMIT of the sequence.
I use reason to formally conceive that there are infinite sets. It's easy: I understand the property of being a natural number; and I understand the idea that given a property, there is the set of things that have that property (with some restrictions on that principle). — TonesInDeepFreeze
Reason is utterly insufficient to determine if there are infinite sets.
The only thing that guarantees the existence of an infinite set is the axiom of infinity.
If we adopt the axiom of infinity, there are infinite sets. If we reject the axiom of infinity, there are no infinite sets. It's as simple as that. The existence of an infinite set is purely a matter of accepting or rejecting the assumption that says there is an infinite set.
Therefore reason can not possibly determine the matter. It comes down to a personal choice, since both the affirmation and negation of the axiom of infinity are consistent with the other standard axioms.
It's easy: I understand the property of being a natural number; and I understand the idea that given a property, there is the set of things that have that property (with some restrictions on that principle). — TonesInDeepFreeze
Your principle leads directly to a contradiction. The restriction needed to patch the problem is restricted comprehension, which would already require there to be an infinite set that's a superset of the infinite set you wish to conjure. Without the axiom of infinity, THERE IS NO SET containing all the natural numbers.
One problem though does haunt me: Every arithmetical statement is either true or false. — TonesInDeepFreeze
No. Just no. Given an arithmetical statement (a syntactic entity) AND AN INTERPRETATION of the symbols of that statement (semantics) then the statement becomes true or false.
Example: Given X and Y, there is Z such that Y + Z = X.
This is TRUE in the integers; and FALSE in the natural numbers.
So you are wrong that every arithmetical statement is either true or false. Absent an interpretation, a statement has no truth value at all. -
Continuum does not existI don't see a need for disagreement here. — TonesInDeepFreeze
I don't either. I agreed with you. I originally said that the extended reals are essentially a notational convenience. As are the names of the numbers in decimal notation, as I indicated.
I agreed with your point. But that doesn't mean we shouldn't use notational conveniences.
You can notate as you wish; and I can say why I also use that notation but like to point out that 'inf' is dispensable when we unpack, which has a pedagogical purpose: Many people, such as in Internet threads, are clueless about axiomatic, rigorous mathematics, so they stubbornly assert that the notation with 'inf' must mean that it names a certain entity. So it is instructive to explain that it is merely contextual notation that does not invoke any entities other than real numbers and a function. — TonesInDeepFreeze
It does name a certain entity; namely the larger of the two extra points in the extended real numbers. I hope you'll give that Wiki page a read, it's not bad as Wiki pages go. -
Continuum does not existSo there is no need to involve an object named 'inf'. It's a more parsimonious approach. — TonesInDeepFreeze
I did say that the extended reals are essentially a notational convenience. Technically we could live without them. But why? By that reasoning we should call googolplex SSSSSSS...SSSS0 with the appropriate number of successors. But isn't better?
Notation is all about convenience of expression.
After all, when you write, "0 = the limit of the function 1/x where x ranges over the positive natural numbers," what do you mean by limit? Do you mean that for all epsilon there exists a delta such that ... etc? Where does your definitional parsimony end? If I say, "Let X be a topological space," should I replace that with, "Let X be a set along with a collection of its subsets satisfying ..." and then repeat the definition of a topology? That would get tedious fast. -
Continuum does not existI take from fishfry (as an analogy in my thinking) that the extended reals have a point of positive infinity (inf) that is like w in this sense: inf is not itself an integer, but it is an extension that comes after all the integers. And w is not itself a natural number, but it is an ordinal that comes after all the natural numbers. — TonesInDeepFreeze
Yes.
https://en.wikipedia.org/wiki/Extended_real_number_line
The extended reals are used so that we can write things like and . They're essentially a notational convenience in calculus and real analysis.
I learned from experience in the supertask thread that it's easier to explain indexing the limit of a sequence as a point at infinity, rather than introducing the concept of the ordinal .
Only on rare occasion. Normally, Infinity for me means unbounded. I don't work on the Riemann sphere. Yes, projective stuff is there in the background, like circles with infinite radius are lines, etc. But I am very old fashioned. Here is the sort of thing that has interested me. — jgill
Thanks for that interesting link. I seem to remember you talking about this a while back.
My point was just that you've seen hypothetical points at infinity, they are nothing new or strange. They come up in many difference contexts. -
Continuum does not existIf only the standard analysis of the reals had been discussed, with infinity not a member and infinitesimals not (re)introduced, perhaps things would have terminated long ago. Maybe not, but I would guess most physicists don't dabble in non-standard analysis nor are they concerned with the roles of ultrafilters in pointless topology. I could be wrong but even introducing ordinals into the discussion opens a Pandoras Box. Just my opinion. — jgill
As a complex analysis guy you use the hypothetical point at infinity of the Riemann sphere all the time, don't you? It's just the one-point compactification of the plane. The circle is the one-point compactification of the real line, and the extended reals are the two-point compactification. -
Continuum does not existYour penchant for making discussions personal leads you astray. — TonesInDeepFreeze
I've been watching you insult the OP for days now. Project much? -
Continuum does not existThe formulation you gave doesn't mention that the ordering includes the standard ordering on w; it only mentions that every member of w is greater than -inf and less than inf. — TonesInDeepFreeze
LOL. Pedants 'Я' us. -
Continuum does not existThe standard ordering on the real numbers is not a well ordering. So talking about points of infinity as in the domain of a sequence is confusing at best. — TonesInDeepFreeze
It's a pedagogical point. It's far far easier for people to understand the point at infinity as the index of the limit of a sequence, than to explain the ordinal ; even if the latter is more mathematically precise. But in this context it makes no difference whatsoever.
I learned this at length in the supertask thread. The idea is to communicate and educate, not to stand on pointless pedantry at the risk of confusing people. Try to consider this point.
In fact if it makes you happy, I'll just tell you that is my own personal notation for what everyone else calls , and now you have no possible objection.
I won't be further responding to this silly and trivial subtopic, but lest anyone think I'm thereby conceding the point, I'm not. Your obsessive pedantry is leading you astry. From now on when I say, "extended natural numbers" just remember that this is my pet name for and all will be well. -
Continuum does not existYou can call them whatever you want. — TonesInDeepFreeze
Consider the following set
with the order
for
Why do you refuse to call that the extended integers, and the subset of nonnegatives the extended naturals; and to write (so far) two posts objecting to this simple and natural terminology?
See this SE discussion. The consensus seemed to be that they're not generally useful; not that the terminology, which is perfectly obvous, is wrong.
https://math.stackexchange.com/questions/1442961/extended-integers -
Continuum does not existI wouldn't, but suit yourself. — TonesInDeepFreeze
If you believe in the extended reals, just setminus all the finite non-integers and you're left with the integers along with the two points at infinity. Why on earth can't you call that the extended integers; or taking the nonnegative ones, the extended naturals? It's perfectly ... natural. -
Continuum does not existNot "extended natural number". — TonesInDeepFreeze
I have no problem with that terminology which avoids getting into ordinals, which people find confusing. I learned that in the other thread. -
Continuum does not existThanks. So you simply extend the natural number to the extended natural number and resolve the problem of indexing. — MoK
Yes exactly.
The difference between an arithematic infinity and a spacial/geometric one is that in the former the numbers have no spatial size and can thus sum to a finite sum. In the latter there are infinite instantiated steps, hence Zeno. — Gregory
The geometric idea is exactly the same.
Consider the half-open unit interval [0,1) which includes 0 and excludes 1. It has length 1. Now break it up into an infinite union of many subintervals:
[0,1/2) [1/2, 3/4) [3/4, 7/8) [7/8, 15/16) ...
That's a geometric decomposition of an interval of length 1 into pairwise disjoint subintervals of lengths 1/2, 1/4, 1/8, ... respectively, representing the arithmetic infinite sum 1/2 + 1/4 + 1/8 + ... = 1.
You can toss in the right endpoint of 1, which, being a point, has length 0 and makes no difference to the length.
Wikipedia has a 2-dimensional version of this visual proof.
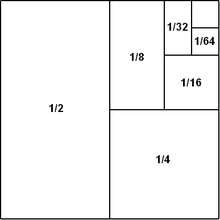
-
Continuum does not existThat is an infinite sequence. I am however interested in the sequence first mentioned by Zeno in Dichotomy Paradox in which the infinite member exists. Each member of the above sequence is finite, so you cannot use the above sequence to give indexes to all members of the sequence in Dichotomy Paradox since the infinite member exists. — MoK
Do you know what a limit is? The sequence 1/2, 1/4, 1/8, ... has 0 as a limit.
If you read through the supertask thread that's been referenced elsewhere in this thread, I explained that you can view the index of the limit as the ordinal number or as a hypothetical "point at infinity," just as plus/minus infinity are hypothetical points at each end of the real number line in the extended real numbers.
https://en.wikipedia.org/wiki/Extended_real_number_line -
Continuum does not existI mean you cannot give indexes to all members of an infinite series. — MoK
1, 2, 3, 4, 5, 6, ...
Is that not an infinite sequence? (You mean sequence. A series is a sum)
It it not indexed by the natural numbers?
Take the sequence 1/2, 1/4, 1/8, 1/16, ...
That's an infinite sequence. It's also indexed by the natural numbers 1, 2, 3, ...
In fact every infinite sequence is indexed by the natural numbers, by definition.
If by dense you mean that there exists a point between two arbitrary points then I understand that applies to the set of rational numbers. The link you provide is technical for me and I have to put more effort into understanding it. — MoK
I agree that the Wiki article could be more clear.
The point is that we say that a linearly ordered set is dense if between any two elements, there is a third strictly between those two.
Another definition is that between any two elements are are infinitely many distinct elements between the two.
These two definitions are equivalent. The argument is exactly the one that you originally gave: that you just keep taking midpoints. -
Continuum does not existCorrect. — MoK
Correct meaning you understand that the rationals are dense but not continuous?
How about considering the point between two arbitrary points, namely a and b, to be mean, namely (a+b)/2? — MoK
Haven't we been doing that all along? Not sure what you mean. The rationals are dense and so are the reals. But the rationals are not Cauchy-complete. They lack the least upper bound property. So you can't use denseness to characterize the continuum, since the rationals are dense but not complete. The rationals are full of holes.
If not, could you please define the continuum for tim wood in plain English? — MoK
The set of standard real numbers, as you yourself have defined it since the first post in this thread, when claiming it doesn't exist. I believe you've now come around to accepting that it does exist. So that's the mathematical continuum. The real numbers.
ps -- Technically, what I've described is a linear continuum.
Formally, a linear continuum is a linearly ordered set S of more than one element that is densely ordered, i.e., between any two distinct elements there is another (and hence infinitely many others), and complete, i.e., which "lacks gaps" in the sense that every nonempty subset with an upper bound has a least upper bound. — Wikipedia
The official definition of a continuum is too general for our purposes here. -
Continuum does not existWe say that the set is continuous if there is a point between any arbitrary pair of points — MoK
Are the rationals continuous?
Between any two rationals there is another rational, right?
But the rationals are full of holes. For example the set of all rationals whose square is less than 2 has no least upper bound in the rationals. Can you see that?
Besides, a totally ordered set with the property that there is a point between any other two is called dense. Have I not previously drawn your attention to this fact? It's the definition.
https://en.wikipedia.org/wiki/Dense_set -
Continuum does not existNo one said anything about ZF. — TonesInDeepFreeze
I did. I said that if there are infinitely many things in the world AND that ZF applies to them, then questions of higher set theory become subject to physical experiment. It's an interesting point.
But if it is taken that there only finitely many things in what is designated as 'the real world', and it is regarded that there is no injection of an infinite set into a finite set, then the question is thereby settled, regardless of ZF; — TonesInDeepFreeze
Of course if there are no infinite sets in the world, then there is surely no continuum in the world.
also, as far as I can tell, the other poster's call to Zeno's paradox or other supertask paradoxes would be unneeded. — TonesInDeepFreeze
I noted that supertask discussions have no bearing on any aspect of reality. -
Continuum does not existThat's fine with me. And if you object to saying "injection" rather than "1:1 map" that's fine with me too. I'm not the one asking whether there is a 1:1 mapping (whether you wish to rule out calling that an 'injection') from the set of real numbers into whatever is designated by 'the real world'. Perforce, obviously, I'm not claiming that if there were such a 1:1 relation then its range would be a mathematical set. — TonesInDeepFreeze
Ok. Injection it is. The rest of my point holds. If there is an infinite collection of anything in the physical world; and if ZF applies to the infinite collections of the world; then questions of higher set theory become questions of physics, in principle subject to experiment. That presents many problems for those claiming there are actual infinities in the world. -
Continuum does not existFirst, again, I don't know what the poster means by "the real world" so I don't know what firm and clear notion there is of an injection from the set of real numbers into "the real world". — TonesInDeepFreeze
The world that is studied by physics. The phenomena around us that are amenable to experiments. Things that have mass, electric charge, velocities, and so forth.
As opposed to conceptual things like numbers, abstract geometric shapes.
I'm not sure what point you are making to ask what is meant by the real world.
The real numbers are a mathematical abstraction. The question is whether it is literally instantiated -- that's the word I prefer -- in the real world.
In other words, is there a true mathematical continuum in the world?
I am not sure what you are trying to get at with this question, since the answer is either obvious, or else you are making some subtle point along the lines of "what is reality?"
Also, the argument "There are no relevant experiments regarding surrounding aspects of the reals, therefore there is no such injection" requires the premise, "If there is such an injection, then there are relevant experiments regarding surrounding aspects of the reals". But how would we rule out that there could be an injection but no relevant experiments regarding surrounding aspects of the reals, or that there could be an injection but no known relevant experiments regarding surrounding aspects of the reals? — TonesInDeepFreeze
Also BTW, "injection" is the word YOU are using. I reject it utterly. An injection is a technical term in set theory. An injection is a type of function between two sets. There is not a shred of evidence that the objects in the real world -- the tables, the chairs, the electrons, the quarks -- obey the axioms of ZF as they pertain to infinite sets. Of course finitary ZF, also known as combinatorics, applies to the objects of the real world. But it's doubtful that anything in the real world is infinite, let alone satisfies the axioms of the real numbers.
So when you say injection, what can you possibly mean? What is your target set? Any injection from the reals must necessarily have an infinite range (or codomain, whatever the hell is the contemporary term. I gather that range and image are different now than when I learned them, and I never heard the word codomain till recently).
Clearly there's no injection from any infinite set to any collection of objects in the real world that we know of. The number of atoms in the observable universe is finite. Start there.
The question was about an injection. — TonesInDeepFreeze
No, that's your word. I use instantiation, in the sense that the von Neumann ordinal we call 12 is instantiated by a carton of eggs. For there to be an injection you'd need a set, and perhaps you can nail that part down for me.
What is the definition of "instantiated in the real world"? Does it just mean that there is the range of an injection from the set of real numbers? — TonesInDeepFreeze
No not at all, since I strongly doubt there is an injection from the real numbers to anything in the physical universe. I doubt there's even an injection from the integers.
But the idea of a physical continuum is that below the Planck length, at the smallest level of reality, we find a copy of the real numbers. A mathematical continuum satisfying the second-order axioms of the reals. The least upper bound property and all that jazz. Metric completeness. All the Cauchy sequences converge. You ain't got nothin' like that in the world as far as anyone knows.
I don't know that that is the case. Moreover, cutting back to the question of an injection, I don't know that that the lack of someone thinking up an experiment would entail that there is no injection. — TonesInDeepFreeze
But it must be so. If there is a set of physical objects (quarks, universes, whatever) with the cardinality of the reals, we can ask what Aleph number it has, and there must be a definite answer. It would be a question amenable to physical experiment, even if we can't do it this week.
Instead of the Large Hadron collider we'd have the Colossal Continuum Counter. What a cool experiment that would be. The Superconducting Colossal Continuum Counter.
I hope you are seeing my point. If there is a set in the world cardinally equivalent to the reals, then we can in principle aspire to count them and see which Aleph they are.
Moreover, would entertaining that there is an injection from the set of natural numbers N into the real world entail that there must be some experiment to conduct? — TonesInDeepFreeze
Oh hell yes! We could count its subsets and see which Aleph they are. Same problem as for the reals, but expressed a little differently.
Or we could verify the axiom of choice. I think a countably infinite set would do, since it has uncountably many subsets.
I'm sure you can either see exactly what I'm talking about, or else you're not seeing what I'm talking about at all. In which case I should await your response.
I don't know that that is true. — TonesInDeepFreeze
Over the years I have Googled around. If someone has proposed an experiment to relate set theory to the world I might well have heard of it. In fact there are a smattering of papers relating set theory to physics, but they'er all behind academic paywalls.
That might be the case. Indeed, even the question alone of the existence of an injection from the set of real numbers into "the real world" doesn't seem to me to have, at least so far, been given a firm and clear meaning. — TonesInDeepFreeze
It has a perfectly obvious meaning. There is a familiar injection from the abstract number 12 to a carton of eggs (a standard dozen). There is an injection from the number 5 to the members of a basketball team.
Nobody has any idea whether there's an injection from a countable set to anything in the real world. But if there is, AND if ZF applies to the world (a darn good question IMO) then there is automatically an uncountable set, namely the powerset of the countably infinite set. And then AC and CH and all the large cardinal axioms become questions of physics.
That might be the case; I don't know. But I don't see that to entertain that there might be an injection entails that there must be an experiment to conduct. But again, the question of the existence of an injection from the set of real numbers into "the real world" doesn't seem to me to have, at least so far, been given a firm and clear meaning. — TonesInDeepFreeze
Please tell me why you say this.
It's perfectly clear what injections from finite sets to the world mean. It's perfectly clear that all finitary combinatorial math applies to the real world.
It's perfectly clear what an injection (or instantiation) of an infinite set would mean.
My point, which I'll bold, since it's really the only thing I have to say, is:
If there is an infinite set in the world, then all the questions of higher set theory become questions of physics, in principle amenable to physical experiment.
Heck, we did the LIGO experiment. If we can detect gravitational waves, why can't we count the points in a continuum?
Answer: Because there is no contnuum in the real world. If there were, the physics postdocs would be all over it.
I wouldn't think that to entertain that there is an injection from the set of reals into the real world entails that there is a physical version of Banach-Tarski. — TonesInDeepFreeze
Of course it would. Well ok I need a bit more. I need a three-dimensional Euclidean space. That's the minimum requirement. The isometry group of Euclidean 3-space contains a copy of the free group on two letters, which is what powers the B-T theorem.
So I'll concede that a mere linear or 2-D continuum is insufficient for B-T.
But again, the notion of such an injection is not definite enough for me to have much of a view anyway (as well as I'm not prepared to discuss details of Banach-Tarski). — TonesInDeepFreeze
All you need is Euclidean 3-space.
I surely don't have a strong opinion on the question of the existence of an injection from the set of real numbers into "the real world", but at least I would want to ponder whether the question is even even meaningful to either affirm or deny. — TonesInDeepFreeze
Well it's a meaningful question, to which I'm prepared to argue that the answer is NO. -
0.999... = 1Do you (two) think that I'm talking rubbish, or does this fit with what has happened to you? — Ludwig V
The Democrats used to be the party of the working class. They've become the party of the wealthy liberal elites and the poor who benefit from government services.
In other news from merry old England, I hear Labour has it in for the House of Lords.
Don’t ‘reform’ the Lords – abolish it
https://www.spiked-online.com/2024/09/12/dont-reform-the-lords-abolish-it/ -
Continuum does not existWhat arguments are you referring to that there is no injection from the set of real numbers into "the world"? — TonesInDeepFreeze
Here's my (meta-)argument.
If the real numbers are instantiated in the real world, then questions such as the axiom of choice and the Continuum hypothesis become subject to physical experiment.
Since no physics postdoc has ever applied for a grant to study such matters, I conclude that no physicist takes these questions seriously; and that in any event, such questions are so far beyond experimental investigation as to be meaningless.
Let me put it another way. If the real numbers have representation in the physical world, do you think there are physical nonmeasurable sets? If so, does that make the Banach-Tarski theorem a fact of the physical world?
Doesn't the absurdity of ever investigating such questions argue against the physical reality of the real numbers?
Supertasks have been used to show there isn't such a mapping for some cases. — Relativist
This I disagree with. Word games involving supertasks tell us nothing about physics. -
Continuum does not existI didn't ask for a proof that shows that aleph_0 is the least infinity but to show that X is the least infinity namely aleph_0. — MoK
A set is defined to have cardinality if it can be bijected to the natural numbers.
Clearly the natural numbers can be bijected to the natural numbers, via the identity map; that is, the function that maps each natural number to itself.
If X is the cardinality of the natural numbers, X is by definition.
fishfry

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum