Comments
-
Political Spectrum Test
Yes but you three certainly have more agreements between you, than you would with me for example.Interestingly, though, I seem to disagree with you and BC as much as agree. — jamalrob -
Schopenhauer's Transcendental Idealism
You are the one using a fiction. You rely on seeing those lines being curved in a Euclidean analogy to non-Euclidean geometry to say that they are curved in non-Euclidean geometry which is patently false.You are proceeding in the exact opposite way of reality, away from reality instead of toward reality. You base your unreal claim that two dimensional geometry is true by referring to a fictitious scenario. Then, you claim that you can only understand the true nature of space by altering it. But that's only because you are starting from your fictitious 2d assumptions, then claiming that the only way to make the reality of space compatible with you fictitious assumptions is to alter it. You fail to realize that the proper procedure is to alter your fictitious assumptions, because you cannot alter the reality of space. — Metaphysician Undercover
The straightness of a line is governed by its intrinsic curvature. Non-Euclidean curvature is an extrinsic curvature - space itself is curving. This has nothing to do with the straightness of the line - with its intrinsic curvature. -
Schopenhauer's Transcendental Idealism
No it's really no illusion at all. If you are a two dimensional creature living your live on a two dimensional piece of paper which is curved to form a cylinder, when you're walking around the cylinder on a curved line, you yourself necessarily perceive it to be a straight line, and cannot perceive it as curved. The only way you can infer the curvature of your space, is if you find a way to alter it. We have found a way to alter it in our case - when the sun is between the earth and certain stars, it alters the curvature of the space between earth and those stars, and hence alters our measurement of their position, which we compare to when the sun isn't between the earth and those stars. If you cannot alter the curvature of your space, you cannot even know that it exists, except obviously by other signs such as you walk in a straight line and return to where you started from.To say that it "appears as a straight line", indicates that you recognize this as an illusion, which is not the true reality of the situation. — Metaphysician Undercover -
Political Spectrum Test
I haven't seen a lot of those points of divergence asked.That is just one point of divergence mate. The test asks 100 and averages it. — Emptyheady -
Political Spectrum Test
Maybe theoretically, but practically, most people would not consider me libertarian. For example thinking the state should prevent the population's access to drugs isn't libertarian. If I go to the libertarian party holding such views, I'd be thrown out :PMeaning, you lean more libertarian than you care to explicitly admit. — Emptyheady -
Political Spectrum Test
Meaning?I think the test knows you better than you know yourself. — Emptyheady -
Philosophy is an absolute joke
Funnily enough, Epictetus wasn't a skeptic though ;)So you've read Chrissypus.... — Cabbage Farmer
What exactly do you mean by the habits and attitudes associated with wholehearted skepticism? If you look through the history of skepticism, these have been very different, varying with the time in which the skeptic lived. Skepticisim, precisely because of its non-assertive nature, can lend itself to a multitude of values and practices, including religion (see Johann Georg Hamann) or atheism (Hume), etc. even in the same time period.I agree with you, that cure should mean more inculcation of the habits and attitudes associated with wholehearted skepticism. — Cabbage Farmer
What is this "form of reason"? Have you been reading Livingston's Philosophical Melancholy and Delirium where he goes on explicating exactly this line of thought traced from Hume, in a somewhat Hegelian/dialectical fashion?it's hard for me to resist the thought that skepticism (properly understood) shows the tracks of human rationality, traces the form of reason, marks the outlines of a discipline of reasonableness, and is that very discipline. — Cabbage Farmer -
Schopenhauer's Transcendental Idealism
This is correct.3D space doesn't require a fourth spatial dimension in which to curve. The Universe could be a hypersphere - a compact curved spherical 3D space - but it wouldn't mathematically need to float in a larger space like a planet in a void. — apokrisis -
Schopenhauer's Transcendental Idealism
No it doesn't give rise to the world in a causal (empirical) sense.Either the thing in itself gives rise to the world we experience or it is utterly disconnected from it; which would make it irrelevant to us. — John -
Schopenhauer's Transcendental IdealismIf you look here
https://en.wikipedia.org/wiki/Geodesic#/media/File:Spherical_triangle.svg
You see straight line AC (actually a curve from our point of view, but a straight line from the point of view of being embedded in the curved space)
From point B to AC, the shortest distance is still the perpendicular little a (also a curve from a point of view external to that space, but from the point of view internal to it, it is a straight line) -
Schopenhauer's Transcendental Idealism
This is irrelevant though. A geodesic appears as a straight line to observation - in fact, it actually is a straight line in a curved space. Non-Euclidean geometry includes Euclidean geometry - Euclidean geometry occurs when space simply has 0 curvature. But that the perpendicular is the shortest distance between a point and a line holds true in either Euclidean or Non-Euclidean space. In Non-Euclidean space, the perpendicular straight line (or geodesic) is still the shortest distance.I am not a physicist, but I understand that this is the case with 4d space-time. Space-time is curved according to the principles of general relativity. Do you know what a geodesic is? — Metaphysician Undercover -
Schopenhauer's Transcendental Idealism
Yes it is >:O (which is the point I've been making all along) Now let me address your other postLet's suppose there is a "space-in-itself". Isn't this contradictory to Schopenhauer? — Metaphysician Undercover -
Political Spectrum TestThis one was actually the absolute worst in my opinion... the questions were so biased, I couldn't even answer them properly. It's like being asked if I'm still beating my wife... One statement: "Individuals have the freedom to decide what they knowingly and voluntarily consume"... What am I supposed to say to that? Obviously the answer is yes, but the state must still restrict and combat drugs and other harmful substances, which the public, out of its own stupidity, would otherwise resort to. But clearly if I answer yes it puts me as a libertarian, which I'm clearly not...
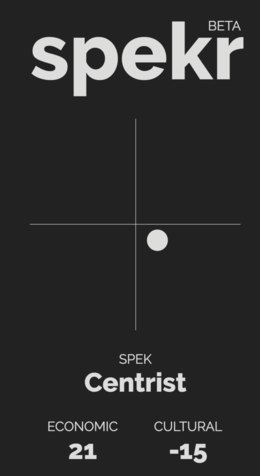
-
A Simple Argument against Dualism
Well, it is clear how two material things can interact, in fact just as clear as how two ideal things can interact. They can interact because they are one substance. If a basketball is made of atoms, and a a football is also made of atoms, then they can interact, if they collide, by virtue of the simple fact that they cannot share the same position in space, so when they come in contact with each other, something must happen.the question of how something material and something non-material can possibly interact seems to presuppose that it is clear how two material things interact. — The Great Whatever
Hence because they are pre-theoretically obvious and abundant, we adopt a one substance view with two parallel attributes...because then we can do the same with physical and mental activity, the correlations between which are even pre-theoretically obvious and abundant. — The Great Whatever
Dualism is fucked up precisely because it cannot account for correlation - it creates two separate realms, which aren't even correlated to begin with! Their correlation becomes an unsolvable mystery. -
Schopenhauer's Transcendental Idealism
Only if you replace Schopenhauer's conception of the thing-in-itself for Kant's (in other words, only if there is no possibility for a space in-itself)I think the same general objection applies to Kant as it does to Schopenhauer's metaphysics. — Wayfarer
Non-Euclidean geometry includes Euclidean as merely a subset of it, when the curvature of space is 0.But one question is, does non-Euclidean geometry invalidate Euclid's fifth postulate, or does it simply show that it's applicability is limited, in a way analoguous to how Newton's laws of motion were shown to have limited scope with the advent of relativity? — Wayfarer
The opinion is divided over Kant's transcendental idealism, because some people postulate a space in-itself, just like the partially examined life you yourself link to.Likewise, from what I am reading about the issue, opinion is divided as to whether non-Euclidean geometry actually invalidates 'transcendental idealism' — Wayfarer
This must be just false, since it assumes that our space is not curved - if space itself is curved, then you'd actually see it as a straight line.That is we would see for example a ball following a curved geodesic in spacetime as curved in space and through time and not a straight line
Yes indeed. How is it possible for there to be a conflict? Because there is a space-in-itself whose effects we notice, despite our inability to perceive this space-in-itself. This is a materialist re-appropriation of Kant, which is very common in today's world, but Kant (and Schopenhauer) would never ever agree to such interpretations. For them, space is intuited - any geometry always involve some a priori perception. You cannot even have a geometry formed of principles which are not synthetic - any conception of space must make a reference to perception (Sensation), and not just Understanding (concepts). So the only thing that can save Kant is noumenal space. If you admit noumenal space, you're a materialist, end of story. So Kant's project as he conceived it, is all but dead.he must revise his conception of the relationship between understanding and intuition (accounting for the possibility of conflict and a posteriori, non-intuitive conceptions of space). -
Schopenhauer's Transcendental Idealism
John has forgotten that the principle of causality which he presupposes in asking the question applies only to the phenomenon (empirical reality) not to the thing-in-itself.The monism itself is the answer. In being timeless and undifferentiated,all of the many changes in the world have no impact on how it is expressed. If individual spatio-temporal forms affected it, it would be differentiated and no longer by timeless. — TheWillowOfDarkness -
Schopenhauer's Transcendental Idealism
The old trope - there's no explanation but I'll go on believing it >:OHow would I know? Perhaps God put them there to confuse us...or perhaps the science is simply wrong and will be corrected in the future, when we have more information (if the species can manage to survive that long). — John -
Schopenhauer's Transcendental Idealism
You're trying to ask what causes the thing-in-itself to be so and so - that's stupid, nothing causes it, because causality applies only for the objectification of the thing-in-itself (the empirical states) not for the thing-in-itself qua thing-in-itself.But where in an utterly undifferentiated timeless unity do those forms come from. This is the perennial Parmenidean problem with monistic conceptions of reality. — John -
Schopenhauer's Transcendental Idealism
Right so if they're not due to the curvature of space, what the fuck are they due to?! :sWe experience effects, which we (perhaps incorrectly) infer to be due to curvature of space. All inferences are fallibilistic. We do not experience space as curved. — John -
Schopenhauer's Transcendental Idealism
Yes we can. Have a look here ;) it's called a convex mirrorI'd go one further. Sometimes we do perceive it outright. We draw examples of it all the time. It's even possible someone could see it out in the world. All it would take in an aura of plane, lines, etc. in the right places of someone's visual experience-- much like seeing any other part of the world. — TheWillowOfDarkness

-
Schopenhauer's Transcendental Idealism
Hegel regurgitation!You haven't given any cogent account at all of how something completely timeless and undifferentiated can manifest itself in either individual spatio-temporal forms, or in timeless forms or in a temporal Will or in temporal wills — John
I have given a means for how it does so. It does so via the forms of space, time and causality. -
Schopenhauer's Transcendental Idealism
Yes you do experience its effects. And if space isn't curved, and space is an a priori form provided by the mind, where the hell are those curved effects coming from? Unless you can answer this question you can say bye bye to your Kantianism.But you have not shown that any experience, as opposed to merely inferences from mathematical models and observations, does refute Euclidean geometry. We infer that space is curved; we do not experience it as curved. — John -
Schopenhauer's Transcendental Idealism
Ultimately yes, hence why you experience it in time.If the thing in itself is the noumenal and Will is not it, but rather merely "close to it", then is Will phenomenal? — John
Yes, your brain is working well in logical deductions.It must be part of the phenomenal if it is "conditioned" by "only one of the categories", or even one of the categories, because the categories, although they are themselves transcendental "condition" only the phenomenal, not the noumenal. — John
They are glimpses of the noumenon, they are obviously still individuated, hence why they are not thing-in-itself. The thing-in-itself qua thing-in-itself is not experienced as an empirical state. The Platonic ideas can be experienced, but not as phenomenon (the subject-object distinction breaks off during such experiences - they are merely the grades of the objectification of the thing-in-itself).And what about the platonic ideas? are they noumenal? If they are then how can there be more than one idea. — John
They are different in degree of objectification/individuation of the thing-in-itself. One substanceAnd if all four the noumenal (timeless) the ideas ( timeless) the Will ( temporal only) and the phenomenal ( temporal and spatial) are different form one another, then how are there not four ontological categories? — John
That was a quick job. I'm waiting for another one.Unless you can give cogent answers to these questions you should be beginning to see why Schopenhauer's ontology is a hopeless mess that doesn't need to be refuted by any geometry; it refutes itself. — John -
Schopenhauer's Transcendental Idealism
Yes, but as Schopenhauer told you, it takes a genius to imagine from the very imperfect information one has, to what is actually the case X-)Any "vendetta" is a product of your own imagination. — John -
Schopenhauer's Transcendental IdealismYour only other escape is to run away "Ahh but Kant is talking just about our perception" but again we do perceive non-Euclideanness in the world. So where is that non-Euclideanness coming from? From the things-in-themselves? Then good luck with your noumenal space ;)
-
Schopenhauer's Transcendental IdealismBut regardless, if you're not such a Kantian, then yes, if NE geometry refutes S it would also refute K. And it quite simply does as far as I see at the moment - if the cognitive faculties provide a priori the forms in which experience is given, then no experience can contradict those forms - because by default they are provided on an a priori basis, and since experiences are constructed in those forms, they cannot but share those forms. If no experience can contradict those forms, and intuition gives us, on an a priori basis, an Euclidean space, then experience does contradict those forms - as seen in physics. Thus we must reject the premise that the forms are a priori, or we must reject the premise that our pure intuition is of an Euclidean space. Take your pick.
-
Schopenhauer's Transcendental Idealism
No he doesn't, but future Kantians do ;)Kant does not ever refer to "space in itself" as far as I am aware or can remember. Can you cite a reference for this? — John -
Schopenhauer's Transcendental Idealism
That was outlined in the OP largely and in subsequent postsWell, I would say that first we must ascertain exactly what his transcendental idealism consists in before we can discover whether it is threatened by non-Euclidean geometry — John
That is not needed, as S's transcendental idealism can clearly be treated as independent of Kant's, given their ultimately strong disagreements.To do that it will certainly be helpful to bring Kant in, since Schopenhauer's TI is an adaptation of Kant's — John
No this doesn't follow, because Kant allows for space in-itselfI would also say that if non-Euclidean geometry turns out to refute Schopenhauer's TI, then it will necessarily also refute Kant's. — John -
Schopenhauer's Transcendental Idealism
This just isn't true. You don't recognise the thing-in-itself at all for Kant. It's just a big X with no understanding of it at all. No understanding even what that X is meant to be, or what it stands for... That's why many of the Kantians who came after, even today, are seriously seriously deluded... you have Kantians speaking of space in-itself >:OSo of course it is, as much for Kant as for Schopenhauer, 'a "mystery" we conceive and recognize". — John -
Schopenhauer's Transcendental IdealismWell your shallow reading of Schopenhauer and comparison with Kant is just as offtopic as your reciting to me some of Hegel's insights, however, I might actually gain something from the latter, while I definitely won't gain anything from the former. Both of them will be a waste of time considering the purpose of this discussion, but at least one has the potential of being interesting.
-
Schopenhauer's Transcendental Idealism
Well it presupposes bracketing it, to say the least, as it's not what is under discussion.I would say this context if discussion relies on dismissing Kant's understanding of noumena. — TheWillowOfDarkness
Yes, I agree, so this discussion isn't for him, he's free to open another to discuss the differences between Kant and Schopenhauer's conception of noumenon if that's what he's interested in. I selected Schopenhauer's transcendental idealism for this discussion because that's the only one I find philosophically interesting - he obviously doesn't.To even address the question you are asking, one has to accept Kant's account is mistaken. John isn't willing to do that, even in imagination. — TheWillowOfDarkness -
Schopenhauer's Transcendental Idealism
I disagree with this. There can be no situation where measurement would indicate that the perpendicular from a line to a point isn't the shortest distance from the line to the point. If you think there can be, please conceive of and give me such an example.hat this is true, is proven with measurement, and when we measure we apply mathematics. Geometrical principles are proven with mathematics.
The problem is that this process of proving, measuring, is an empirical process. — Metaphysician Undercover
Not if space is a form that the mind supplies a priori...So let's take the basic principle, the shortest distance between two points is a straight line. That there is a separation between two points assumes that there is something between them. This we call space. So even to demonstrate that there is separation between two points requires an empirical process, so all geometrical concepts are fundamentally a posteriori. — Metaphysician Undercover
Not necessarily, I could theoretically build a ruler long enough and measure it. And even if it did take sending a light beam, I fail to see how this disproves that the perpendicular is the shortest distance... Perhaps if you could explain this in more detail or give an illustration via youtube or somehow.To measure this separation, something such as a beam of light must traverse the space between point A and point B. This requires time. Due to this passing of time, the shortest distance between two points is no longer considered to be a straight line. — Metaphysician Undercover
Right, so then you're a transcendental realistreality of space imposes itself onto the forms which our minds produce, forcing us to change what we may have previously considered to be a certainty. — Metaphysician Undercover
Where is this a priori certainty coming from?First, there is a necessary equality of units, and second there is a necessary order. Each of these may be an a priori certainty. — Metaphysician Undercover
The thing-in-itself is ultimately real, while the phenomenon is only real qua phenomenon and not as thing-in-itself.What do you have in mind as a "controlling factor"? — Metaphysician Undercover -
Schopenhauer's Transcendental Idealism
How is it pertinent to the OP? The OP is "can S's transcendental idealism survive the challenge posed to it by non-euclidean geometry?" And in fact, we're not one inch closer to answering this than we were before all this mumbo-jumbo. That means that our discussions have failed.If you want to avoid discussing the relationship between Kant's and Schopenhauer's conception of noumena and phenomena, which is very pertinent to the OP — John -
Schopenhauer's Transcendental Idealism
Yes.We might say that Schopenhauer says we know the-thing-itself, that it is a "mystery" we conceive and recognise — TheWillowOfDarkness
It seems to me that John is merely carrying out his personal vendetta though, with little interest to the underlying philosophy. As you can see, the statements that irk him is that I consider Schopenhauer more correct than Kant - as if my personal judgement on the relative correctness of Schopenhauer in comparison with Kant actually mattered in a discussion of Schopenhauer's transcendental idealism with reference to non-euclidean geometry :sI think I do: Schopenhauer doesn't treat the thing-in-itself like an empirical state — TheWillowOfDarkness -
Schopenhauer's Transcendental Idealism
Right, things-in-themselves don't exist then >:O How about you cite me some of Hegel's insights, as a shallow reader of Hegel I'd be more interested in that, than hearing about your shallow reading of Schopenhauer.You didn't read what I wrote about Kant's attitude to things in themselves, and simply quote a phrase out of context. So, you are repeating the same mistake as Schopenhauer by imputing a claim, that things in themselves exist, to Kant that he quite explicitly disavowed. — John -
Schopenhauer's Transcendental Idealism
The Will is closer to thing-in-itself than Representation as it's only conditioned by one of the categories, time, and not the other ones. However, later Schopenhauer disavows and walks back on the identification of Will as Thing-in-itself and returns to the thing-in-itself being unknown - an unknown which is nevertheless non-dual.So, according to you, the thing in itself is not identified as Will by Schopenhauer? It's "one substance" involving quadruple aspect theory, then? — John
And there is no quadruple aspect theory. Will is the ground of the phenomenon. Platonic Ideas are encounters with and glimpses of the thing-in-itself through art, or mystical experiences. The thing-in-itself is the unknown ground or source of the Platonic Ideas and of the Will. So it's still double aspect - Phenomenon composed hirearchically of Will and then the other Representations, and Thing-in-itself. -
Schopenhauer's Transcendental Idealism
It's merely sharing what I think. I don't have to back up everything I say, especially when it's totally unrelated to the topic and a quick reply about a side conversationDid I say your statements "irked" me? I just can't see the point in making statements if you are not prepared to back them up, however cursorily. — John
Things in themselves are incoherent. If space/time/causality are what individuates things, then there cannot be individual things apart from space, time and causality.'things in themselves' — John -
Schopenhauer's Transcendental Idealism
No that's not the point. The point is WHY he earns the right to property by work, which is the most significant point, otherwise it would be just a meagre assertion.The first passage, as far as I can tell, basically just says that a person earns the right to own property by work. I'm pretty sure that idea was expounded by Locke, and I'm not sure he was the first either. Perhpas you can poiint to what you ( presumably) think I have missed in this passage. — John
Sureeeeee... except that it tells exactly how the imagination functions and how it aids the genius to reach a truth that others cannot even see...The second passage reads like an unjustified romantic paean to the potent powers of genius. I'm not seeing anything great or even insightful in these passages, — John
Yes, especially Hegel X-)So my impression has long been that Kant and Hegel are philosophers of far greater stature than Schopenhauer, and nothing you have quoted here has done anything to change that opinion. — John
Nope. One substance ontology involving double aspect theorydualistic ontology — John
Thing-in-itselfhe also tries to incorporate Platonic Ideas as something like universal forms governing the process of individuation from undifferentiated will to differentiated representation, but he seems to give no account of whether they are part of Will (noumenon) or part of Representation (phenomenon) — John
Platonic Idea (out of time)
Will (in time, but out of space and causality)
Representation
This is roughly the hirearchy, your account shows merely a shallow misreading of Schopenhauer.
Agustino

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum
