Comments
-
A -> not-AI think P2 excludes the possibility of the C1 disjunctive introduction and therefore foils the entire argument. — NotAristotle
If P1 is true then C1 is true. Therefore, the inference is valid.
You seem to be suggesting that if both P1 and P2 are true then it's possible that C1 is false? -
A -> not-AI see no inference rules being applied in an explosion hypothesis and therefore cannot see it as a deduction at all. — NotAristotle
I explained it above.
P1. I am man
C1. Therefore, either I am a man or pigs can fly (from P1, using disjunction introduction)
P2. I am not a man
C2. Therefore, pigs can fly (from C1 and P2, using disjunctive syllogism) -
What is real? How do we know what is real?I'm afraid I'm somewhat handicapped here, in that I don't really understand what reality-in-itself is. — Ludwig V
As an analogy, let’s assume that I’m trapped in a windowless room. Something enters the room. I can see that it exists and what it looks like and how it behaves now that it’s in the room, but I don’t know that it existed or what it looked liked or how it behaved before it entered the room (or after it leaves); perhaps it’s very different (or doesn’t exist) when not in the room.
In this case “being in the room” is an analogy for “being seen”. -
A -> not-AI get what you are saying. However, I maintain that it is strange for me to think of the initial argument of this thread as "valid." — NotAristotle
What do you think "valid" means? It just means that the conclusion can be deduced from the premises using the rules of inference. It doesn't mean that the argument is sound or cogent.
but the principle of explosion is also nonsensical to me. — NotAristotle
1. Either I am a man or pigs can fly
(1) is true if either "I am a man" is true or "pigs can fly" is true. Therefore, we can deduce (1) from the premise "I am a man". This is called disjunction introduction:
P1. I am a man
C1. Therefore, either I am a man or pigs can fly
Separately, we can deduce that if (1) is true and "I am a man" is false then "pigs can fly" is true. This is called disjunctive syllogism:
P1. Either I am a man or pigs can fly
P2. I am not a man
C1. Therefore, pigs can fly
So what happens when we combine the two?
P1. I am man
C1. Therefore, either I am a man or pigs can fly (from P1)
P2. I am not a man
C2. Therefore, pigs can fly (from C1 and P2)
From the contradictory premises "I am a man" and "I am not a man" we have deduced the conclusion "pigs can fly". We can deduce anything from a contradiction. This is part of the reason why we agree that contradictions are impossible. -
Consciousness and eventsFrom what I vaguely understand, the idea is that the wave-function is a universal wave-function, i.e that the universe as a whole is in a superposition, not just the cat, so there is a universe in which the cat is alive and a universe in which the cat is dead. So any physical measuring device is also in a superposition and cannot act as an "outside observer" capable of collapsing the universal wave-function; only something that is not a part of the universal wave-function can do that. The (non-physical) mind is the presumptive candidate.
The alternative view is that the universal wave-function doesn’t collapse and so both universes are real, leading to the many-worlds interpretation.
Or superposition is epistemic, not ontological, leading to de Broglie-Bohm theory. -
Consciousness and events
-
The American Gun Control Debate
I don’t understand what you’re trying to argue. If it’s just that my likelihood of surviving a knife attack is greater if I have a gun than if I’m unarmed, then I agree, but it’s incredibly myopic and naive to think that this proves anything.
You need to look at the bigger picture; at what actually happens in the real world.
The epidemiology of self-defense gun use: Evidence from the National Crime Victimization Surveys 2007–2011
Self-defense gun use (SDGU) occurs in fewer than 1% of contact crimes.
...
SDGU is not associated with a reduced risk of victim injury.
...
Of over 14,000 incidents in which the victim was present, 127 (0.9%) involved a SDGU. SDGU was more common among males, in rural areas, away from home, against male offenders and against offenders with a gun. After any protective action, 4.2% of victims were injured; after SDGU, 4.1% of victims were injured. In property crimes, 55.9% of victims who took protective action lost property, 38.5 of SDGU victims lost property, and 34.9% of victims who used a weapon other than a gun lost property.
...
Compared to other protective actions, the National Crime Victimization Surveys provide little evidence that SDGU is uniquely beneficial in reducing the likelihood of injury or property loss.
Then consider the high levels of gun violence more generally that come with high levels of gun ownership. There are so many mass shootings, school shootings, and other gun homicides in the USA. Yet somehow their citizens are safer because they have a gun that they can putatively use in self-defence?
It seems like their defence of gun ownership is a fantasy that contradicts the actual facts.
I'll stick to what the statistics and studies show. My country is safer with strict gun control, and so I'm glad that we have it. -
The American Gun Control DebateUnfortunately, if someone is out to seriously hurt you, they will have considered it as well. — Tzeentch
And as I said before, if someone is out to seriously hurt me then I’d rather neither of us have guns than both of us have guns.
I’m unlikely to be sniped to death with a knife from 200 yards whilst I’m busy debating college students. -
The American Gun Control DebateI'm talking about fending off a knife fighter and you only have your bare fists. — Tzeentch
Running away is perhaps the most effective option.
Also, I agree that wars would be less deadly without guns - they would be less deadly for the side made up of criminals fighting against the side made up of law-abiding, normal people.
It would be a landslide for the criminals. — Tzeentch
I don't understand what you're trying to say here. -
The American Gun Control DebateYou know what, maybe they are not effective, but they're a hell of a lot more effective than your bare fists I'll tell you that much. — Tzeentch
I'm much more likely to survive a fist fight than a gun fight. -
The American Gun Control Debate
Comparing street crime to warfare is a false equivalency. But that said, I'm 100% certain that wars would be less deadly without guns (and other long-range weaponry). -
The American Gun Control DebateAnd I would much rather have "the great equalizer" as ↪Outlander called it. — Tzeentch
Perhaps if we have a pistols-at-dawn duel, but that's not the reality. It's drive-by shootings, someone pulling a gun on you before you know what's happening, being shot at a distance and from behind, etc.
And according to this, "overwhelming evidence demonstrat[es] that firearms are not an effective means of self-defense." -
The American Gun Control DebateUK and many other countries in Europe including my own are turning into shitholes. The sense of safety that once was is now just an illusion. People feel safe because they had the good fortune not to be confronted with reality, which is that if they cross paths with the wrong people the authorities can't and won't do a single thing. — Tzeentch
Also see this:
Seventy-eight per cent of people in England and Wales think that crime has gone up in the last few years, according to the latest survey. But the data on actual crime shows the exact opposite.
As of 2024, violence, burglary and car crime have been declining for 30 years and by close to 90%, according to the Crime Survey for England and Wales (CSEW) – our best indicator of true crime levels. Unlike police data, the CSEW is not subject to variations in reporting and recording.
The drop in violence includes domestic violence and other violence against women. Anti-social behaviour has similarly declined. While increased fraud and computer misuse now make up half of crime, this mainly reflects how far the rates of other crimes have fallen.
All high-income countries have experienced similar trends, and there is scientific consensus that the decline in crime is a real phenomenon. -
The American Gun Control DebateI think you had to delete what you wrote because you could be arrested for it. I couldn’t imagine. — NOS4A2
I deleted it because in my haste I was putting words in your mouth, which may have been unwarranted. Perhaps you weren't referring to government tyranny but crime, like Tzeentch above. -
The American Gun Control Debate
If this is a reference to criminals then I'll repeat what I said to NOS4A2 before: I’d much prefer it if they don’t have access to guns, even if that means I don’t have access to guns either. -
The American Gun Control DebateMany Americans see what is happening to the UK and it only reaffirms the reasons we should never give up our guns. — NOS4A2
What things? -
A -> not-AIn what world is "1 and 2 therefore not 1. 1 and 2. Therefore, not 1." a sensible or logical maneuver? It most certainly is not modus ponens so understood. — NotAristotle
The bottom line shows modus ponens. It doesn't matter what A and B mean:
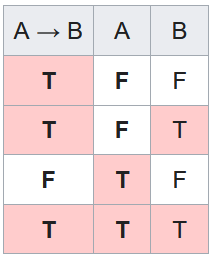
Now replace B with ¬A. Only one line has both A → ¬A and A true, and on that line ¬A is also true. That's all it means for the argument to be valid.
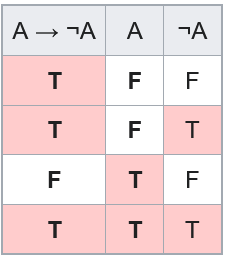
However, two of the lines are removed by the laws of excluded middle (the top) and non-contradiction (the bottom)
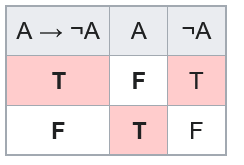
That gives us:
A → ¬A
∴ ¬A
Or
A
∴ ¬(A → ¬A)
So the argument is unsound. -
The American Gun Control DebateIs that so irrational in your eyes? Am I such a bad guy for holding such a sentiment? — Outlander
No, but the reality is that easy access to guns seems to lead to an increase in gun deaths, school shootings, etc.
So you have to ask; is it worth it? Charlie thought so. The British didn’t. I think we made the right call.
And in 30 years, we haven't changed our minds, even across party lines. Perhaps because we've seen what happens in the USA.
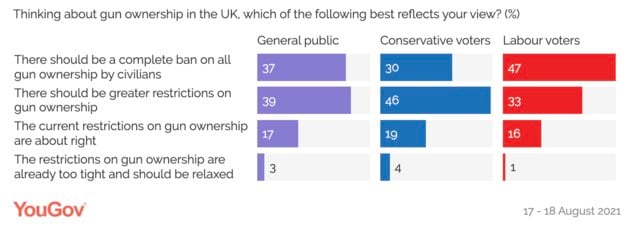
-
The American Gun Control DebateOkay. A school shooting (a few dozen dead kids) is bad. A war, my friend (a few million dead kids) is worse. There are no excuses or way to sideline or "talk around" that fact. Without a right or means to defend oneself from an oppressive government, the darkest desires which often control people imbued with the mindset to seek power over others, such becomes inevitable. And don't give me that "a rifle cannot defeat a military jet or drone" nonsense. Soldiers and police are people too who want to go home to their families who literally wake up each day knowing they prevent indiscriminate killing of their own countrymen. They're not going to do that and the average low-level enforcement (cops) will be less likely to.risk their lives over a clearly immoral order that would likely end in one or more of their own deaths.
Not to mention, societal collapse. Historically, basically all nations are "roving gangs" temporarily turned civil due to access to resources that belonged to other people. There are no good people left, for the most part. We're literally the worst of humanity, artificially propped up by violence and theft. That's all there is to it. Ticking time bombs waiting to go off. Of no purpose or value but what we delude ourselves into thinking. Meaning, an individual who chooses to live a private life without engaging in (basically forced and compulsory) social membership with strangers because "I don't want to die" (AKA fear) should have a right to reasonably defend himself from a group of marauders, something only possible with a semiautomatic (or higher) firearm. All current institutions and groups were ultimately based and established on the principle of fear. Fear is not solid ground. — Outlander
So you think frequent mass shootings at schools is a price worth paying because it's theoretically possible that society will collapse or that the government will become a tyranny and start executing innocent citizens?
I'm more of a realist. The UK has had strong gun control for almost 30 years, and nothing like that has happened. Compared to the USA I'd say we're much safer, have more rights, and actually hold our politicians to account.
But hey, if the zombie apocalypse happens then I'll eat my words (if I'm not already eating someone's flesh).
The UK does seem to be having a lot of machete and knife fights on city streets now though don't they. — Sir2u
Better that than guns.
Sorry to disillusion you about this, but the bad guys will always get weapons while weapons continue to exist. — Sir2u
And yet we haven't had a school shooting since strong gun control has been in place. -
The American Gun Control DebateWhy don't you trust other people to make the right decisions? — Outlander
I’ve seen what happens in the USA. It happened in Scotland in 1996, and it was that that brought in gun control here. We haven’t had a school shooting since. -
The American Gun Control DebateThere are crazies out there and people who hate you and wish death upon you because they don’t like what you say. — NOS4A2
And I’d much prefer it if they don’t have access to guns, even if that means I don’t have access to guns either.
I’m happy with the UK law on gun ownership. It’s not because I don’t believe in rights; it’s because I think that private gun ownership is too dangerous. -
The American Gun Control DebateEveryone keeps mentioning this statement here and elsewhere, without citation. It’s an odd phenomenon because clearly it is not something that you all remember hearing or reading before his murder, assuming that you never followed his debates and conjured it from memory. I never heard it before but I’ve read it a bunch of times today. Was it passed around on Reddit or Bluesky or something in the wake of his assassination? — NOS4A2
https://x.com/Ronxyz00/status/1965872119604289791 -
The American Gun Control DebateShooting at another school as well: https://edition.cnn.com/2025/09/10/us/at-least-2-students-shot-denver-area-high-school
The tragedy marks the 47th shooting that took place at a school in the United States so far this year — 24 of which were on college campuses and 23 on K-12 school grounds.
As an outsider to American gun culture, I think it's a shame that so many agree with Charlie Kirk, who once said "I think it's worth to have a cost of, unfortunately, some gun deaths every single year so that we can have the Second Amendment to protect our other God-given rights. That is a prudent deal. It is rational. Nobody talks like this. They live in a complete alternate universe." -
Idealism in ContextYour position is anti-realist, while mine is pragmatic and operational. — JuanZu
These are not mutually exclusive. See scientific instrumentalism, which argues against scientific realism, claiming that scientific theories are neither true nor false but only useful/successful or not.
Also related to this is Stephen Hawkings’ model-dependent realism, which despite the name is a brand of instrumentalism. -
Idealism in ContextWe sometimes are wrong about how things are. How can this be possible if there is not a way that things are, independent of what we believe? — Banno
The wording here seems susceptible to equivocation.
Consider this argument:
P1. Only John's mind exists
P2. John believes that something other than his mind exists
C1. Therefore, idealism is true and John has a false belief
So that there is a "way things are, independent of belief" isn't necessarily that mind-independent objects exist.
You and I agree as to what is the case. How is that possible unless there is something external to us both on which to agree? — Banno
John and Jane both agree that God exists. It doesn't then follow that this agreement is made possible by the existence of some third thing, i.e. God. God might not exist. -
An unintuitive logic puzzleI might seem dismissive and like I'm refusing to accept it — flannel jesus
I know that I've come across this way too and I don't mean to be. -
An unintuitive logic puzzleI think adding "we all know the same thing" is something unnatural you added tbh. — flannel jesus
It's not.
Everyone knows that Arguments A and B are valid, because they are and everyone is a perfect logician.
I see 99 blue and 100 brown.
If I have blue eyes then every person with blue eyes sees 99 blue and 100 brown.
If I have brown eyes then every person with brown eyes sees 99 blue and 100 brown.
Everyone with my eye colour knows that either A1 or B1 is true.
Therefore everyone with my eye colour has come to the same conclusion: that if we all commit to the rule "if the people I see with eyes don't leave on day then I will leave on day and declare that I have eyes" then everyone will leave the island having correctly declared their eye colour.
So I commit to this rule, as will they — and we leave the island having correctly declared our eye colour without anyone having to say anything. -
An unintuitive logic puzzlebut they all know they could, and they all, according to you, know exactly the same thing, so they all know they should subtract 95 and it would still work. — flannel jesus
They could subtract 95, but that would be arbitrary and so they wouldn't do it. Perfect logicians would stick to the non-arbitrary . -
An unintuitive logic puzzle
Again, subtracting an arbitrary number from is arbitrary, and so perfect logicians wouldn't do it. But isn't arbitrary. -
An unintuitive logic puzzleYes but you don't know that every person will do that. Therein lies the problem — flannel jesus
Then we move on:
1. If I have blue eyes then every person with blue eyes knows exactly what I know
2. If I have brown eyes then every person with brown eyes knows exactly what I know
Either way, I know that everyone with my eye colour knows exactly what I know, and so knows that if every person commits to the rule: "if the people I see with eyes don't leave on day then I will leave on day and declare that I have eyes" then everyone will leave the island having correctly declared their eye colour.
I put it to you that if perfect logicians know that everyone with their eye colour knows that committing to this rule will work then they will commit to this rule, and so they will leave the island having correctly declared their eye colour. -
An unintuitive logic puzzlethe point you were focusing on is it's validity. — flannel jesus
Yes, that's the first step: arguments A and B are valid.
The next step is: premises A2 and B2 are not arbitrary.
And the next step is: I know that either A1 or B1 is true.
Therefore, I know that if every person commits to the rule: "if the people I see with eyes don't leave on day then I will leave on day and declare that I have eyes" then everyone will leave the island having correctly declared their eye colour. -
An unintuitive logic puzzlebut you also know it's a valid argument if you replace a2 and B2 with this premise: — flannel jesus
Yes, but adding or subtracting some arbitrary number to or from is arbitrary, whereas isn't arbitrary. -
An unintuitive logic puzzleit might be — flannel jesus
It is.
it exists in a sea of equally valid and arbitrary premises. Suppose they replace 2 with committing to leave on X + 5 days. Or even X - 10 days. — flannel jesus
The premises aren't arbitrary. is the number of people seen with eyes. Adding or subtracting some arbitrary number to or from would be arbitrary though, which is why perfect logicians wouldn't do it.
Next we consider Argument B:
B1. There are 99 people with blue eyes and 101 people with brown eyes
B2. Every person commits to the rule: "if the people I see with eyes don't leave on day then I will leave on day and declare that I have eyes"
B4. Therefore, from (B1) and (B2), every person with blues eyes commits to the rule: "if the 98 people I see with blue eyes don't leave on day 98 then I will leave on day 99 and declare that I have blue eyes"
B5. Therefore, from (B1) and (B2), every person with blues eyes commits to the rule: "if the 101 people I see with brown eyes don't leave on day 101 then I will leave on day 102 and declare that I have blue eyes"
B6. Therefore, from (B1) and (B2), every person with brown eyes commits to the rule: "if the 99 people I see with blue eyes don't leave on day 99 then I will leave on day 100 and declare that I have blue eyes"
B7. Therefore, from (B1) and (B2), every person with brown eyes commits to the rule: "if the 100 people I see with brown eyes don't leave on day 100 then I will leave on day 101 and declare that I have brown eyes"
B8. Therefore, from (B4), every person with blues eyes leaves on day 99 and declares that they have brown eyes
B9. Therefore, from (B7), every person with brown eyes leaves on day 101 and declares that they have brown eyes
This argument is also valid.
Now we get to the more interesting part. If we know that these arguments are valid then so too do our islanders. They might not yet know if any of the premises are true, but they do know that the arguments are valid.
For the next step let's start by considering a simplified version of the argument in the OP. The islanders arrive on the island together and are told that everyone has either blue or brown eyes — which is not the same as being told that there is at least one person with blue eyes and one person with brown eyes (it could be that everyone has blue eyes or everyone has brown eyes); it is only meant to dismiss the possibility that one's own eyes are green or red or pink or whatever.
I am an islander.
I know that Arguments A and B are valid.
I see 99 people with blue eyes and 100 people with brown eyes. Therefore I know that either A1 or B1 is true.
Therefore, I know that if every person commits to the rule: "if the people I see with eyes don't leave on day then I will leave on day and declare that I have eyes" then everyone will leave the island having correctly declared their eye colour. -
An unintuitive logic puzzleSeems like it requires mind reading to me for them to assume that about everyone else.
If they all could assume that about everyone else, sure, they get off the island. But they have no idea what everyone is committing to. — flannel jesus
I'm not assuming anything about anyone. I am simply saying that Argument A is valid. -
An unintuitive logic puzzleWhy would one of these blue eyed people think of that particular premise? — flannel jesus
I'm not saying that they are. I'm simply saying that the argument is valid. -
An unintuitive logic puzzle
You're getting ahead of yourself. I'm not yet talking about what the people on the island see or know. I am simply saying that Argument A is valid.
I'll break it down even further if it helps:
A1. There are 100 people with blue eyes and 100 people with brown eyes
A2. Every person commits to the rule: "if the people I see with eyes don't leave on day then I will leave on day and declare that I have eyes"
A4. Therefore, from (A1) and (A2), every person with brown eyes commits to the rule: "if the 99 people I see with brown eyes don't leave on day 99 then I will leave on day 100 and declare that I have brown eyes"
A5. Therefore, from (A1) and (A2), every person with brown eyes commits to the rule: "if the 100 people I see with blue eyes don't leave on day 100 then I will leave on day 101 and declare that I have blue eyes"
A6. Therefore, from (A1) and (A2), every person with blue eyes commits to the rule: "if the 99 people I see with blue eyes don't leave on day 99 then I will leave on day 100 and declare that I have blue eyes"
A7. Therefore, from (A1) and (A2), every person with blue eyes commits to the rule: "if the 100 people I see with brown eyes don't leave on day 100 then I will leave on day 101 and declare that I have brown eyes"
A8. Therefore, from (A4), every person with brown eyes leaves on day 100 and declares that they have brown eyes
A9. Therefore, from (A6), every person with blue eyes leaves on day 100 and declares that they have blue eyes -
An unintuitive logic puzzle
As shown above, the argument is valid when there are 100 people with brown eyes and 100 people with blue eyes but invalid when there is 1 person with brown eyes and 1 person with blue eyes.
Therefore, it's not the case that if the argument is valid when there are people with brown eyes and people with blue eyes then it is valid when there are people with brown eyes and people with blue eyes.
The number of each colour makes a difference. -
An unintuitive logic puzzleif I don't agree with your conclusion we can't continue. Yeah okay buddy. I don't know why you want to talk to anybody lol. This is a philosophy forum. We can disagree with you, don't be weird about it. — flannel jesus
It's not my conclusion. It's one of my premises. And it's a premise that I demonstrated to be true here. -
An unintuitive logic puzzlesure it follows — flannel jesus
No it doesn't.
If you can't accept that Argument A is valid then we can't continue.
Michael

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum



