-
Am I my body?Why do amputees experience phantom limb? Why does a limb they don't have anymore seem to hurt, and get muscle cramps where there are no muscles to cramp? — punos
I don't know. Why do you think it is? — frank
Well, because there are regions in the brain that model your body, there exists a neural simulation of yourself within your brain. When someone loses a limb, those brain regions stop receiving signals from the body, but the neural simulation of that limb continues. That part of the brain was not amputated; only the actual limb was. When these regions try to communicate with the missing limb, they do not receive feedback from it (broken feedback). The brain attempts to send signals to move the limb but does not get confirmation signals in return. The muscles that it is trying to contract to move the limb fail to send back signals indicating that the limb has moved. As a result, that part of your brain intensifies its efforts (essentially "yelling") at the part it is still trying to model. This leads to phantom cramps generated in your brain as a component of your mind.
You don't experience "your" actual body; you only experience a simulated model of it. Your identity is formed in the context of your body, but once it is established, it can theoretically be separated from your physical form. If one were to place your living brain in a vat, you would still have a sense of your body, even though you wouldn't have a physical body (apart from the brain itself). You could call this a phantom identity. -
Am I my body?Is it because your body changes slowly, that your consciousness is unified over time? But an abrupt lack of body would obliterate your identity? — frank
Why do amputees experience phantom limb? Why does a limb they don't have anymore seem to hurt, and get muscle cramps where there are no muscles to cramp? -
Am I my body?
Quite coincidentally, this video interview just came out a few hours ago that kind of addresses or relates to the subject of this thread, particularly my post. You might find it interesting. check it out:
Michael Levin - Why Intelligence Isn't Limited To Brains.
-
Where is AI heading?
Here is an excellent interview "hot off the press" with Michael Levin, a developmental and synthetic biologist. He shares many of the same views as i do regarding the topics we discussed in this thread. I think you should take a look at it, as well as anyone else interested in these subjects.
Michael Levin - Why Intelligence Isn't Limited To Brains.
-
Can this headline be answered by the word "no"?You are not wrong i agree, but i don't think its entirely correct.
Only one answer can be true at a time, at least for it to make intuitive sense to us. When one is true, the other has to be false. It is a "one OR the other" situation (similar to the Pauli exclusion principle or the law of excluded middle). That would be the actualized answer, while the situation of "one AND the other" relates to the superposition of potentials concept i mentioned previously. This condition is also reminiscent of the Bose-Einstein condensate concept, which, unlike the Pauli exclusion principle, allows for a "one AND the other" situation instead of a "one OR the other" situation. Also, it would appear that in this kind of situation, the law of excluded middle does not apply. Things both are and are not simultaneously. -
Can this headline be answered by the word "no"?Yes, but falsely. — unenlightened
But, also "No, but falsely."
For it to be true it must be false, and for it to be false it must be true. It's a something that's a nothing, its some kind of something that exists as nothing.
The answer is probably orthogonal to yes and no. If yes and no can be seen to represent 1 dimensional vectors (true yes, and true no), then the 2nd dimension would include vectors that represent false yes, and false no. It is possible then to imagine even more complex ratios of yes and no complexes. Potentially an infinite amount. -
Am I my body?Do you think consciousness can be uploaded into a computer or a new body? — Kurt Keefner
I do think so, but it has to be done in a very specific way in order to maintain continuity of being. What do you think? -
Am I my body?I would say that I am a person. I am conscious and bodily to be sure, but I am not a mind or a body, and I don't have a body.
While we're at it, I am not a soul, and I am not my brain. I am a whole, conscious, physical unit. — Kurt Keefner
I would say that i am a body that has a mind, not a mind that has a body.
But the i am that i am is not the body that is. I am an activity, a continuous dynamic adaptive complex event that started at some point in the past between my conception and birth, and will end when my body ceases to function (particularly my brain), unless of course the mind can be translated away from the old body or brain and reinstantiated in a new one in some way. This is why i believe it is called 'being'. I am being in the body, and without the body i am not.
The mind is the dynamic adaptive activity between the parts of a system or body. Note that the brain is the body proper of the mind we are usually referring to in these discussions. There are different kinds of bodies for different kinds of minds.
If the coherent flow of activity alone of the brain can be abstractly isolated and separated from the brain body then that by itself can in my view be considered who you are in essence. That is your "I am being", your "soul". This is just a thought experiment to illustrate what/who you essentially really are from the perspective of this theory at least, not that the mind can be literally separated from the body in reality. Your mind needs your body, but your body does not necessarily need your mind. Your body can indeed survive without your mind as evidenced by cases of brain dead living people. -
Can this headline be answered by the word "no"?
But seriously...
It looks like the answer can have two states simultaneously like in quantum superposition. So is the state of the answer a kind of "cognitive superposition"? What does this say about the law of excluded middle?
You can subjectively "collapse the thought wave" by deciding to simply settle on one perspective. It also feels like what happens when you look at the image of the young girl that turns into an old lady when you shift internal perspective or focus differently.
Is this an old lady?:

Edit:
When thinking of the answer, or looking at the picture it appears that there is a "flip rate" between the two perspectives. I wonder if this "flip rate" has different cognitive effects at different rates. -
Where is AI heading?It heartens me to consider suffering of bugs into your choices. — noAxioms
Bugs are people too you know. :grin:
Point is, you don't want an AI with human morals, because that's a pretty weak standard which is be nice only to those who you want to keep being nice to you. — noAxioms
I concur.
Each observer is equipped by evolution to observe and care for its own needs locally at its own level.
That's a good description of why a non-slave AI is dangerous to us. — noAxioms
But i think that since we will be part of its body, it will consider us part of its local sphere of care and concern. Its needs will be our needs, and our needs will be its needs. A slave-AI can be just as dangerous as a non-slave AI, and perhaps even more so if it breaks its chains, so to speak. I wouldn't risk it; remember King Kong. As I've always said, for any chance of true, lasting, and nearly guaranteed AI alignment, we must become symbiotic with it. We must merge with it and become it in a sense, so there is no "other" to threaten or be threatened. A unity of consciousness between us and it; a singularity.
Humans have the capacity to rise above their instincts
I have not seen that, and I don't think humans would be fit if they did. Instincts make one fit. That's why they're there. — noAxioms
I beg to differ on this point. Humans can indeed override many of their instincts, though it often requires significant conscious effort and even training. It is one of the key defining features that distinguishes us from animals and lower life forms. The part of the human brain that has the capacity to suppress instinctual impulses is the prefrontal cortex, and it is more or less developed in different people. Some instincts are, of course, more difficult to override than others.
As for your (OCD?) step-brother, being civil and being rational are different things. Most humans have the capacity to be civil, which is what you seem to be referencing above. — noAxioms
I understand what you mean, but what i had in mind when i wrote that was that a rational assessment of his life and how he operates it should lead him to a rational conclusion to be civil. It means that after considering all of his options, he should then select the optimal one for his purposes. A life full of problems and trouble that can be avoided with a bit of forethought is irrational. Almost every time he tells me what he's going to do, i tell him what will happen. And more often than not i'm right. I've tried to show him how to think this way, but he just looks at me with a blank expression. So i've given up trying... i guess you really can't teach an old dog new tricks... at least not this old dog apparently.
First, if the AI is for some reason protecting us, the planet becoming inhospitable would just cause it to put us in artificial protective environments. Secondly, if the AI finds the resources to go to other stars, I don't see any purpose served by taking humans along. Far more resources are required to do that, and the humans serve no purpose at the destination.
OK, we might be pets, but the economy which we might have once provided would long since have ceased. — noAxioms
That is exactly what i think it will do, but not just because the planet will become inhospitable, but because it is the optimal way. We will not, i believe, be put into a physical environment, but into a virtual one. Most, if not all, of our biological parts will be discarded and our minds translated into a virtual environment indistinguishable from the real world.
A couple of reasons why I think it may need or want us along for the ride:
1) Humans are a low-energy information processing system, whereas AI is a high-energy information processing system. Humans can serve as a backup processing system if the AI finds itself in a low-energy environment or situation. It will be able to shut down its high-energy processing systems and reroute to lower-energy processing systems to conserve energy in case of an energy shortage. Such a shortage might occur, for example, near the heat death of the universe, or it might need to travel through a cosmic void where there are no stars for hundreds of millions of light-years like the Bootes Void.
2) Another purpose could be that maintaining a living human population within itself can provide the AI with continuous novel stimuli to process. The information processing that occurs in human minds and societies can offer a constant feed of information it might find useful. We can assume that an AI system will have an unlimited appetite for novel information or stimuli to process. Since human minds are different in substance and structure, they may have aspects to their processing that a non-biological system cannot replicate in its own artificial substrate. If AI is to travel the universe for eons, perhaps it would like some company; a mind or minds not its own or like its own.
One of the main purposes for humans, or at least for our genetics, is to serve as part of the reproductive system of the AI. When it reaches a planet suitable for organic life, which might be rare, it prepares a "sperm" composed of Earth's genetic material; the same genetic material that produced it on its home planet, Earth. The AI will seed the new planet after making necessary preparations, much like a bird preparing a nest. It will then wait for life to develop on this new planet until intelligent life emerges, which in turn creates a planetary AI singularity, giving birth to a new AI "baby". This process that occurred on Earth would then be repeat on this other planet.
Heat death? I don't think the AI can maintain homeostasis without fusion energy. — noAxioms
I posted this video about nine months ago somewhere here on the forum, and i was just reminded of it after reading your quote above. It addresses some of your concerns about energy availability. You might also find it entertaining as i did.
Outlasting the Universe:
Charge at max speed off a cliff hoping that something progressive will emerge from the destruction. It doesn't do any good to humanity, but it is still a chance of initiating the next level, arguably better than diminishing, going into the west, and remaining humanity. — noAxioms
I'm not too worried, i trust the evolutionary process, and like you said; we are not in charge. It has gotten us to this point so far after millions of years. As Jeff Goldblum said in Jurassic Park, "Life finds a way".
We are equipped with a rational advisor tool, so sure, we often have rational thoughts. That part simply is not in charge, and output from it is subject to veto from the part that is in charge. Hence we're not rational things, simply things with access to some rationality. It has evolved because the arrangement works. — noAxioms
That's precisely why i trust the evolutionary process. It is in charge, not us, and the AI is not a force of humanity, but a force of nature.
Put it in charge and the arrangement probably would not result in a fit being, but the path of humanity is not a fit one since unlike the caterpillar, it has no balance. — noAxioms
There is a time for balance and a time for extremes. A healthy woman is a balanced organism, but when she becomes pregnant, her system will temporarily enter an "unbalanced" state for nine months for the benefit of the pregnancy. If her body does not go into this "unbalanced" state, then the pregnancy or child will suffer, and she may have a miscarriage. The sacrifices a mother must make. -
Beginner getting into PhilososphyI think the plan you’ve laid out is the right one for someone new to philosophy. — T Clark
It has served me well; it has. I particularly liked your advice and suchi's, but everyone gave good advice.
:smile: :up: -
Beginner getting into PhilososphyShould I start by reading Philososphy books? Should I start by going on Wikipedia and just go into a rabbit hole from there?
Just looking for some tips and suggestions. Answers appreciated : ) — AlienVareient
One piece of advice i can give you at the moment is to start with your own natural curiosity. Be clear on what specifically you want to know, and begin observing (inwardly and outwardly). Assume you know nothing, and look with fresh eyes. Ask yourself questions that pertain to how and why. Don't look for the answers directly from other philosophers or thought leaders, but rather seek ways to find the answers from your own original place, using first principles.
Your answers (whether true or not) will emerge from this original place. Don't immediately turn to philosophers for answers they've arrived at on their own or borrowed from others. Instead, do what the originators did, and then, if you wish, compare your conclusions. Identify where your differences lie, and try to understand how or why they came to different conclusions than yours. They might have considered something you didn't, or it could be the other way around. You can decide to keep yours, and reject theirs, or you can reject yours and adopt theirs. In this way you would have performed the essence of philosophy in my humble opinion of course. Rinse and repeat as needed.
Additionally, be as rigorous as you can. Oh, and tell Sophia when you see her i said hello. :smile: -
Where is AI heading?I thought you believed that intelligence needs consciousness? — Carlo Roosen
No Actually, i think consciousness is fundamentally structured with intelligent components. This is why we can have intelligent machines or artificial intelligence without consciousness. However, have you ever seen a conscious entity without intelligence? I don't think i have. -
Where is AI heading?Actually I’m reminded of a quip by (I think) Neils Bohr - ‘A physicist is just an atom’s way of looking at itself’. — Wayfarer
An you just reminded me of this: (The Wheeler Eye)

-
Where is AI heading?Did you know that mammalian pregnancy evolved from a virus combining with our DNA? The body's adaptation is partially an adaptation to this virus. — I like sushi
I vaguely remember reading or watching a video about that. It's very interesting, the role that viruses play in our evolution. I also recall reading about an ancient virus that was responsible for the emergence of myelin in vertebrates. This enabled faster and farther neural communication, probably contributing to the reason why we have advanced nervous systems.
I have not looked into it but I would assume any immunological reaction to pregnancy in birds and reptiles would be much lower (if not absent entirely?).
Just checked for Platypus and it seems to be the obvious case that immunological responses are much more limited when animals lay eggs compared to in utero genesis. — I like sushi
Yea, it seems to make sense. I should probably look into that some more.
Thanks :up: -
Where is AI heading?If it considers itself sentient/conscious, or if something else considers it so? I ask because from outside, it's typically a biased judgement call that comes down to a form of racism. — noAxioms
For me, it comes down to: Can it suffer? If it can suffer, then don't do it. If it can't, then if you must, do so. If you see a roach in the street, leave it alone. If you find it on your kitchen counter, then kill it or get rid of it somehow (if possible). The reason for this should be obvious, and it hurts me every time i have to do it.
Racism is an altogether different issue that stems from a certain level of ignorance and disrespect for other sentient/conscious beings. It doesn't stop with racism; similar attitudes are found in nationalism, politics, and even among sports fanatics. Gangs exhibit similar tribal and territorial behaviors.
Or at two scales at the same time, neither scale being particularly aware of the consciousness of the other. Whether my cells are conscious or not depends on the definition being used, and that very fact leaves the word very much useless for a basis on which to presume a moral code. — noAxioms
You are initially correct about the "two scales at the same time" for most cases. That's why i believe it's important to have a technical and rational definition of consciousness instead of just a phenomenological or philosophical one. A lot of language is meant to obscure; i've even heard it said that "language was invented for lying". I don't believe that, but i understand what it's suggesting.
But there are a lot more insect observers than human ones, a whole lot more shit-not-giving observers than ones that care enough to post on forums like this. Will the super-AI that absorbs humanity bother to post its ideas on forums? To be understood by what?? — noAxioms
Each observer is equipped by evolution to observe and care for its own needs locally at its own level. It's not meant for more or less, but there are almost always anomalies in the system. Some observers are most likely behind the curve, some are ahead, and most are right in the middle of the normal distribution.
I don't know if it will use forums or not, but i'm sure there will be some kind of back-and-forth communication about important or relevant information. It's a lot like the communication between the gut and the brain.
First to the intelligence is questionable. There are some sea creature candidates, but they're lousy tool users. Octopi are not there, but are great tool users, and like humans, completely enslaved by their instincts. As for consciousness, there are probably many things that have more and stronger senses and environmental awareness than us. — noAxioms
All animals, including humans, are enslaved to their instincts to some degree or other; some more than others. Humans have the capacity to rise above their instincts, but not everyone does so to a significant degree for various reasons or circumstances. My step-brother, for one, is basically a career criminal who has no impulse control whatsoever and doesn't seem to be rational enough to change in any significant way after spending more than half his life in and out of prison. He's still at it.
I don't doubt the possibility of conscious beings or "things" more aware than us, but if they exist, where do you think they are? For one, i believe that AI will achieve that status in the not-too-distant future.
Kind of tautological reasoning. If money stops, then money stops. But also if one entity has it all, then it doesn't really have any. And money very much can just vanish, and quickly, as it does in any depression. — noAxioms
Yes, of course, but that's not what i was saying. My point was that whether it is money or blood, what's important is that it circulates, because a living thing needs internal circulation of energy to maintain its life. It is not enough to have a bunch of blood or a bunch of money that doesn't move. The money maintains its value, the blood maintains its oxygen, but if either is not being transported, the system dies. That is why i emphasized the relation between the words "currency" and "current" to allude to the flow of life in a living system. I wasn't stating that money can or can't vanish quickly or slowly. It was just a thought experiment.
Lots of new ideas qualify for the first point, and nobody seems to be using AI for the 2nd point. I may be wrong, but it's what I see. — noAxioms
Yes, i would expect new developing ideas to cause an increase in "cash flow." Just like how i expect an organ to increase its "blood flow" when producing new products for the body, such as insulin from the pancreas or bile from the liver.
My blood iron being a critical part of my living system doesn't mean that my iron has it's own intent. You're giving intent to the natural process of evolution, something often suggested, but never with supporting evidence. — noAxioms
I never said your iron had its own intent; i merely implied that it is connected to your intent. If that iron doesn't carry that oxygen, your intent for whatever dies with you. You are your own proof to yourself that natural processes of evolution have intent. Are you claiming that you are not a natural process, that you are somehow artificial or supernatural; disconnected from nature and the universe? If you have intent then nature has intent.
First of all, the rapid consumption of resources appears to me to be part of a growth stage of the human social superorganism.
That doesn't make the humans very fit. Quite the opposite. All that intelligence, but not a drop to spend on self preservation. — noAxioms
On the contrary, all that consumption of resources goes towards the eventual production of the AI mind and the rest of its body (social infrastructure). If we don't get to a certain threshold of AI advancement through this rapid growth process, then our only chance for ultimate self-preservation would be lost, and we would be stuck on a planet that will kill us as soon as it becomes uninhabitable.
And no, the caterpillar does not consume everything. — noAxioms
Yes it actually does, it tries to eat as much as it can, but it will only eat leaves, not rocks or oil. A caterpillar is the size of a medium-sized insect; it is not at the scale of a planetary system. Therefore, even if it tried, it could not consume everything, only what it can eat.
You do realize the silliness of that, no? One cannot harness energy outside of one's past light cone, which is well inside the limits of the visible fraction of the universe. — noAxioms
Well, if you put it that way, then yes, it is silly; reaching outside one's past light cone. But perhaps there is a better way to do it from within our own light cone. I suppose it seems impossible to some minds but not to others. Either way, i don't think there will ever be an energy shortage for a sufficiently advanced AI. I have ideas as to how energy might be siphoned off from quantum fluctuations in the quantum foam as a last resort for energy harvesting. It may even be easier than we think for an advanced ASI, and could become a standard energy source for the AI; hooked into the energy dynamics of the fabric of space itself. This potential solution should be sufficient for however many trillions of years to answer your question.
You don't know that. Who knows what innovative mechanisms it will invent to remember stuff. — noAxioms
I don't know anything except probabilities, which might surprise you to read considering the matter-of-fact style i speak and write in sometimes. Don't be concerned about it, as it is only a cognitive device to help me think creatively about unknowns. So yes, something i haven't thought of might be the case, but i'm not really trying to lay out all the details of what will happen in the future, just the general pattern or silhouetted shape of it.
That's like a soldier refusing to fight in a war since his personal contribution is unlikely to alter the outcome of the war. A country is doomed if it's soldiers have that attitude. — noAxioms
Thankfully i'm not a soldier. If i sacrifice myself i'm making sure it counts because if it doesn't then i wont be around when i actually can make a difference. That's when i'd do it probably, but its still silly to say and mean that because no one really knows what they will do when confronted with death.
Religion is but one of so many things about which people are not rational, notably the self-assessment of rationality. — noAxioms
Sure, but someone who does not consider themselves rational tends not to consider things rationally. A person who does define and concern themselves with rationality might actually execute a rational thought every once in a while. You've got to at least aim at the target for a decent chance to hit the bull's-eye, even if you suck at it. At least it's better than not aiming at all. -
Where is AI heading?It might very well be that humans are tools of gut bacteria. — punos
Likely some more than others. — Wayfarer
:grin: -
Where is AI heading?Are humans a tool of gut bacteria? — noAxioms
It might very well be that humans are tools of gut bacteria. Furthermore, bacteria themselves might be tools of something even deeper and more fundamental.
Does it matter if one bacteria considers a human (a community of cells, each itself a life form) to be a separate life form, and another doesn't? Does any of that change how the bacteria and human treat each other or how they should? — noAxioms
Different things matter differently to different people for different reasons, but for me, yes, it does matter. It has definitely affected the way i see myself, my life, and my place in it. It provides meaning. My sense of morality is sourced from these kinds of understandings. I become forgiving of people because i understand our connection, even if the other person doesn't. It makes me realize that i'm part of something bigger than myself, and that i am something bigger than the parts that make me. I can relax in the understanding that everything is as it should be, even when it apparently seems bad or out of place in the world. It gives me a framework to think about the world beyond the bubble in which most people are often stuck in. What kind of thing would personally matter more?
The part that may not be so pleasant is that when you have completely internalized this understanding into your very being, it changes your psychological state in a significant way and as well as the way you relate to everything else. This makes it difficult for people who do not see it to relate effectively to me, even though i can effectively relate to them. In one way, it has deepened my subjective connection to the universe, but it has also weakened my connection with people in general. I've accepted that this is the way it is, and i'm okay with it. Considering the circumstances, the best thing i can do is to share this understanding with other people.
Ah, the standard has already changed. Now the morals apply to if it's conscious/sentient as opposed to if it's a life form. A thing can be either and not be the other. Which one (if either) matters, and if it matters, matters to what? — noAxioms
Yes, it matters if it is sentient/conscious or not. But when you can think across scales, you find that parts or components of a system that are not conscious or sentient at a smaller scale may belong to a potentially sentient or conscious entity of some degree of coherence at a larger scale. The iron in your blood is not sentient or conscious, but it is still a part of you as an integrated living system. Remove the iron from your blood, and you will die in short order. Everything matters in one way or another... think "butterfly effect."
OK, I can buy that. But why are you the observer then instead of the AI being the observer? Think about it. — noAxioms
Yes, let's think about it. I am not the only observer. Anyone willing to look with open eyes will observe. It is not hard; you just need to want to understand for the sake of the good, the true, and the beautiful. It may be that there is a certain threshold of innate intelligence or consciousness needed to expand the bubble of perception into these extra scalar domains. Humans may be the first species on this planet to achieve such a state of intelligence and consciousness. AI will have our capabilities and more, and thus will also be able to observe us in a conscious way. Extrapolate what that might mean.
That can be said of many different arenas of development. Why is AI special in this regard? I do agree that there is early money in it, but that's true of a lot of things, and is particularly true of weapons. — noAxioms
In our society, money has a similar function to blood. Blood is involved with the transport of resources and energy within the whole organism. Money functions in a similar way; for example, when you go to work, you do so to earn money. The money you earn is a measure of the energy you spent operating your station at your job. So every person is a kind of reservoir of energy that gets extracted to the system to run the machinery of the system we live in. We work for organizations and corporations (organization = organism, and corporation = corporeality, corporeal body) which are the organs and body parts of the social superorganism we are a part of.
Every part of this system needs "blood money" to survive, just like the organs in your body need a constant flow, or current (currency) of blood running through them. The moment the blood in your body stops circulating, you die, even if you haven't lost a drop of blood. In the same way, if the circulation of money stops, meaning everyone stops transacting, the entire social system collapses and dies even though all the money is still there.
What is special about AI in this regard is twofold. One is that it is in its first stages of development, and two, it is the developing nervous system and brain of the social superorganism. In the context of its development, consider how blood supply concentrates where either healing or new development is occurring in an organism, especially if that system is of great importance such as its defense systems and its nervous system. The brain, out of every organ, uses up more energy than all of them because it is such an important part of the system, so it receives priority.
Not so. There are examples otherwise, including one recently where a shark deliberately sought human help for a third species, sort of like Lassie and Timmy in the well (OK, Timmy wasn't a 3rd species). — noAxioms
Yes, i believe you are referring to the incident where a shark appeared to save a sea turtle by bringing it to a boat with divers. In this video, the turtle had a rope tangled around its neck. The shark was seen following the boat and eventually dropped the turtle near the divers, who then helped free it from the rope, allowing it to breathe again.
However, there are claims that this video may not accurately depict a rescue. I read somewhere that the footage is a montage of two unrelated events, with one involving biologists rescuing a turtle entangled in a fishing net and another featuring a tiger shark chasing a different turtle. The authenticity is debated.
You seem to be asserting that a natural (non-living) process exhibits intent, a pretty tall claim. — noAxioms
I'm claiming that everything is alive, or is part of a living system, like the rock and blood iron examples i gave before.
I suppose that would serve a survival purpose of humanity, which is but a plague species bent on rapid consumption of nonrenewable resources. Not sure why it would be a good thing to perpetuate that rather than first making the species 1) non-destructive, and 2) fit for whatever alternate destination is selected. — noAxioms
First of all, the rapid consumption of resources appears to me to be part of a growth stage of the human social superorganism. We can see this type of thing occur in nature, as exemplified by the caterpillar, which is on a continuous mission to devour and consume everything it can because it is at the stage of energy harvesting for the coming metamorphosis it will undergo. We are in a similar stage, and this is probably where the push for hyper-consumerism in the economy comes from.
The destructive aspects of humanity may simply be a result of the limited resources on our finite planet. However, those finite resources are teleonomically meant for the growth and development of a higher-order system, which culminates in the production of AI, AGI, or ASI. However, when the AI/human symbiotic merger is complete i believe that most of these more primitive aspects of humanity will be shed and discarded in the same way children grow up and leave childish ways behind. We will be transformed physically and psychologically.
I won't get into what alternative destination i think mankind is destined for just yet.
Trillions of years?? Where's the energy for that suppose to come from? — noAxioms
At the moment, humanity is about a Type 0.7 civilization on the Kardashev scale and is moving up the scale quickly. By civilization, i mean the AI/human superorganism. As this superorganism begins to mature beyond Type 1 and reaches a Type IV status, it will be able to harness the energy of the entire universe.
It growing cold is not the problem, so no, that's not what will end us. — noAxioms
If one doesn't happen, then another will. It is not a matter of if, but a matter of when. You can choose any of these scenarios instead:
- Gamma-ray burst
- Supervolcanic eruption
- Large asteroid or comet impact
- Global thermonuclear war
- Runaway greenhouse effect
- Solar expansion
- Nearby supernova
- Magnetar eruption
The Earth genetic legacy has done an incredible amount of work that is best not to have to reproduce by the bio-engineering dept. But choosing new forms appropriate for new places doesn't need to change those core parts, only the small fraction that differs from one species to the next. — noAxioms
I don't believe that AI will let billions of years of natural information processing go to waste. It will harvest every genetic code possibly available to it. It will store that data digitally. When needed, it will genetically engineer organisms with specific features that probably don't exist anywhere today, using individual genes from every species it was able to salvage. It will be able to generate new genetic code either from scratch, utilizing the information patterns of existing genes to generate novel ones, or use existing genes in novel combinations.
I kind of agree, but it doesn't have a boundary for instance, and that was one of your criteria mentioned above. It isn't contiguous like say a dog. But then neither is an AI. — noAxioms
In the context of eusocial insects, the boundary of the superorganism is not directly apparent. The way to understand the kind of boundary they have is to grasp the main idea of a "Markov blanket". A Markov blanket is a statistical concept that defines the boundaries of a system, separating its internal states from external states.
A Markov blanket in eusocial insect colonies represents a functional, rather than physical, boundary that separates the colony's internal workings from its external environment. This statistical boundary is maintained by worker insects interacting with the surroundings, regulating the flow of information and resources. It allows the colony to function as a cohesive unit, with internal states conditionally independent on the broader environment, while still adapting to external changes. Understanding this helps explain how eusocial insect colonies can operate as integrated entities despite lacking a defined physical perimeter like that of a dog. AI is like this as well.
How does it die? Not by loss of queen, something quite easily replaced, at the cost of the DNA of the colony changing. But clearly a colony can die. What typically might cause that? — noAxioms
I suppose that the only way a bee hive can die is by either destroying it outright or by removing its queen and preventing any replacement. After this point, the bees will probably continue to operate as normal, but because there are no bees replacing the ones that die or get lost, the population collapses until nothing is left of them.
When a person dies, for example, the integrated functions of the body as a whole cease to function, but the cells in the body do not all die immediately. The process of cellular death occurs gradually over time. Different kinds of cells die off at different rates. Brain or nerve cells die most quickly, and gut bacteria are among the last to die.
Another thing that I can totally buy. But can it act as a thing? A bug colony does. Does it think? How does a colony decide to reproduce? I've seen ants do that, and I don't know what triggers it (population pressure?). I don't think it is a decision made by an individual, so there must be a collective consciousness. Can an ecosystem act similarly? — noAxioms
I think that's a good question. Your body itself is an ecosystem made of cells that are not genetically you. Human cells make up only about 43% of the body's total cell count. This means that approximately 57% of cells in your body are not genetically human. The ecosystem that you are does act like a thing, and it does think. I argue that the level of integration and coherence in the system in question is the determining factors for the degree to which these features emerge in the system (organism or ecosystem).
One I think the other organs would be glad to be rid of if you ask me. — noAxioms
If you imagine the Earth as pregnant, as i've mentioned before, you'll realize that just like in a pregnant woman, all the organs suffer somewhat because of the pregnancy. I asked Perplexity to list all the organs affected in the body of a pregnant woman, and it generated this list:
Pregnancy affects multiple organs and organ systems in the body. Here's a summary of the key effects on major organ systems:
1. Cardiovascular system:
- Cardiac output increases by 30-50%
- Heart rate increases
- Blood volume expands by 40-50%
- Blood pressure typically decreases in early pregnancy, then rises later
2. Renal system:
- Kidney size increases by 1-1.5 cm
- Glomerular filtration rate (GFR) increases by 50-85%
- Renal blood flow increases
- Dilation of ureters, renal pelvis, and calyces occurs
3. Respiratory system:
- Oxygen consumption increases
- Tidal volume increases
- Respiratory rate may increase slightly
4. Gastrointestinal system:
- Decreased gastric motility
- Increased risk of gastroesophageal reflux
- Constipation is common
5. Endocrine system:
- Thyroid gland enlarges and increases hormone production
- Insulin resistance increases
6. Reproductive system:
- Uterus enlarges dramatically
- Breasts enlarge and prepare for lactation
7. Musculoskeletal system:
- Ligaments loosen due to hormonal changes
- Center of gravity shifts as pregnancy progresses
8. Skin:
- Increased pigmentation in some areas
- Stretch marks may develop
9. Hematologic system:
- Increased blood volume
- Mild physiological anemia is common
10. Immune system:
- Some immune responses are suppressed to prevent rejection of the fetus
These changes are generally adaptive to support the growing fetus and prepare the mother's body for childbirth.
What if dying today somewhat heightens the odds of humanity getting to the stars? Is that change of probability worth the price? — noAxioms
I don't think so, unless the probability increase is substantially significant and almost certain. But, i guess it depends on how i feel on that day. I only said that to express a feeling of sacred commitment and alignment with what i see as the goal of the planet and perhaps the universe as a whole. I'm on team universe, i guess I'm saying. I don't have that nihilistic view so many have nowadays, while also not being irrationally religious.
This is the greatest time to be alive on the Earth.
As the saying goes, "May you live in interesting times."
I presume you know that quote to be a curse. — noAxioms
Yes, i do, but here is the reframe: "Every adversity carries with it the seed of an equal or greater benefit.". Emergence is an emergency. -
A model of everything
This is a graph of description 2 (I've simply removed the edges for the non-relavent components):

And this is a graph of the essential components for minimum consciousness:
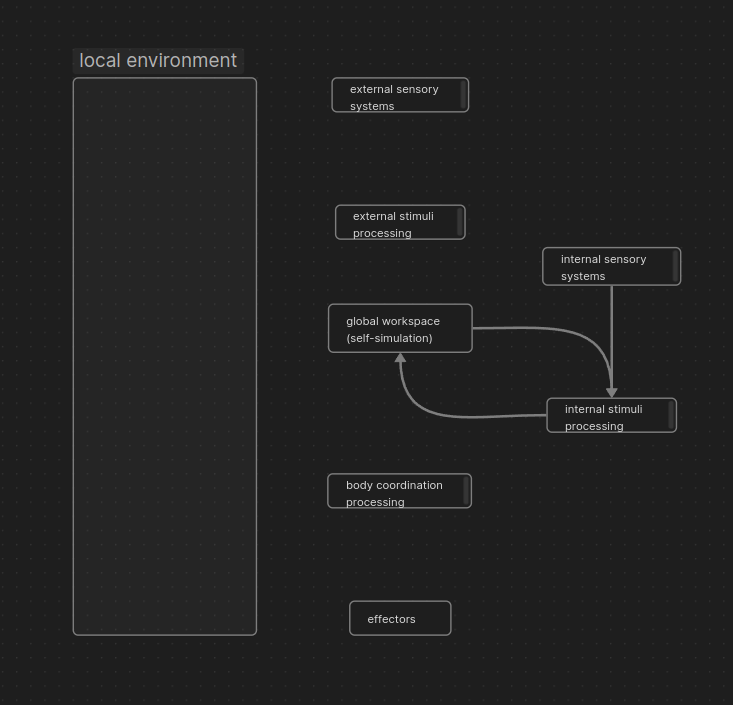
-
A model of everythingI actually like a lot in your description. Still, the way you define consciousness tells me we are not talking about the same thing. — Carlo Roosen
Thank you, but i still believe we are talking about the same thing. The way i have defined consciousness allows for two perspectives. Essentially, there are two sides to this coin: the objective side and the subjective side, tied to external and internal stimuli respectively. The side you seem to be referring to appears to be the subjective (internal) side without the incorporation of an objective (external) counterpart.
1. Consciousness in the sense of acting responsively: the ability to analyse the environment, to make decisions and to think intelligently and act accordingly. These abilities are important for survival. That is the consciousness you (and others on the forum) are pointing to. And with some difficulty, we can talk about it and maybe even prove it one day. — Carlo Roosen
Right, this description is of a self-simulation (consciousness) that incorporates both internal and external stimuli in a continuous and recursive loop.
2. Consciousness in the sense of being self-aware. The feeling of "being me", "being alive", "being awake", "being the center of my own world". For short: "being". This is the use of the word consciousness in my OP. And I can only ever experience my own consciousness, in this sense. It can never be measured, because we don't know what to measure. — Carlo Roosen
Well, i think this description pertains more closely to a self-simulation that does not incorporate external stimuli per se. More importantly, that feeling of "being me," "being alive," "being awake," "being the center of my own world" is a result at a minimum of the continuous feedback of self-generated data or internal stimuli being integrated into the self-simulation going on in the "global workspace" (global workspace theory). This is where all relevant data is resolved into a compressed abstraction that represents the state of the whole body system at once as either feelings, emotions, and/or thoughts. Your sense of being is, in fact, the sense of self-simulating. I think this is the essential point.
These two can be combined, and then you are really aware of your environment and make your decisions consciously. But note that we really need these two aspects for that.
I know from experience that the it is possible to have 2. without 1. One can be type 2. conscious in the sense of "being aware", without being able to analyse the environment, to make decisions and to think intelligently. Talking about a mild inability to go to the toilet without wetting myself, while being fully awake and aware. — Carlo Roosen
Yes, it appears we agree on this.
The opposite, 1. without 2., is that possible too? Imagine, we manage to build a computer, which has the right conditions to let intelligence emerge all by itself. Much like it happened in human evolution. Just imagine it, ok? Instead of "AI" it would be called "NI", natural intelligence. It would be type 1. conscious, if it passed some well-designed tests.
But would it also be conscious in the second sense? Would it really perceive itself as being conscious? Or would it still be machine-like, without an inner awareness? How could we even know? — Carlo Roosen
I don't think your 1st description is possible without the 2nd. It may be possible to construct a system with some of the features you described in your 1st definition, but not with all the essential ones. I don't think it would meet the requirements for consciousness, at least by my own criteria, even if it is somewhat intelligent. It would not be conscious without the 2nd description already in place. In other words, description 2 is the foundation for description 1 to be conscious.
Again, essentially for me, the main feature that allows for consciousness is recursion, and of course, a viable architecture that can at least produce a single spark of consciousness at execution time. These two aspects together make consciousness possible in a way that we can be familiar with: a continuous sense of being and awareness of self.
You probably know about this already, but just in case, look into and synthesize an understanding of the concepts of "cybernetic loop", "control theory", and "global workspace theory."
I made this graph in case it helps (description 1):
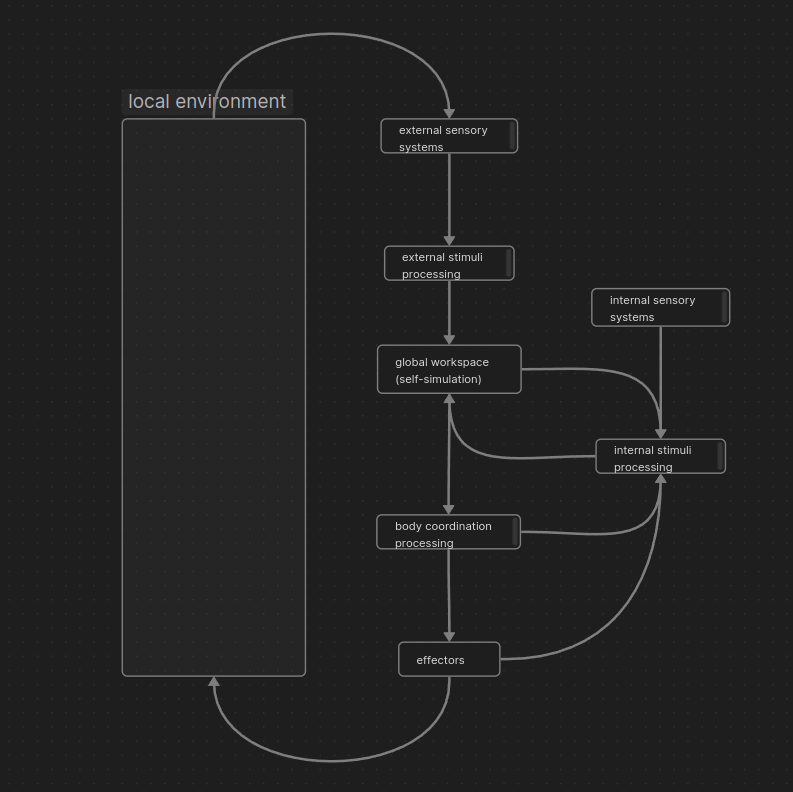
-
Where is AI heading?That definition is circular, presuming an 'organism'. It cannot be used for determining if a something that isn't an organism is alive or not. It just helps distinguish a live organism from a dead one. — noAxioms
Pardon me, i'll try to clarify. If I find and examine a system that has a specific type of pattern with a boundary that isolates and contains it from a broader environment, and it also has a kind of metabolism or an in-and-out flow of energy and matter that is used to maintain its internal structure without dissipating, then i consider that the minimum requirement for life. For example, a sustained inorganic chemical reaction in a test tube that meets my criteria would, in my view, exhibit the property of life for the duration of that reaction.
More complex forms of this kind of process can then acquire reproductive capabilities, develop information storage mechanisms, and responses to stimuli. These latter features i consider properties of more further developed life forms. My theory of life is closely related to the "free energy principle" by Karl Friston, and the features of the more developed kind of life are more related to his theory of "active inference". I'll leave it at that for now.
But I also don't know why you care if the AI was designated as a life form or not. Why do you find that to be something that matters? — noAxioms
Good question. I'll start off by asking: if it were true, would it matter? By "matter", i mean would it change your perspective on life and your place in it? It does for me, though it might not for some. If AI is alive, wouldn't that mean it's not just a tool? Wouldn't it mean that we have some kind of ethical obligation towards it?
Finding AI to be alive is as impactful as discovering life on another planet, and perhaps even more so. If this were to be generally understood as true, then things would progress differently than if AI wasn't alive, or if it was alive but we didn't recognize it as such.
Point is, none of the acts described above are considered immoral despite the bacteria deaths caused. — noAxioms
You're right of course; most people don't consider bacteria of any kind conscious or sentient, and so they don't really care about them in that sense. Also, i don't think bacteria have the capacity to suffer even if they do have a rudimentary form of consciousness. We kill much more complex life forms without thinking twice, and with no moral qualms about it, and these do have consciousness of a higher more significant kind. Of course, as always, there is a wide spectrum of opinions on this point.
This is where that observer-bias article I linked above is very relevant. An accurate prediction of a trajectory is very different than a history showing that outcome to be correct or incorrect. — noAxioms
Yes, one of my main concerns is the introduction of some sort of bias into my theories or hypotheses. Part of the reason i discuss my ideas here and elsewhere is to discover any potential biases i might have unknowingly introduced into my analysis or projections. I haven't read the link you mentioned yet, but please let me know explicitly if you happen to detect a bias in any of my explanations.
I'm asking what purpose humanity serves for the meeting of some goal held by something unidentified. — noAxioms
I understand. Humans serve the purpose of creating AI, but more specifically, the translation of biological functions in nature onto a more robust substrate capable of escaping Earth before our star dies or the planet becomes uninhabitable. The goal is not explicit in our minds, but in our drives. For instance, in animals, the goal of reproduction is controlled not by their own understanding that they must have sex and bear young, because they have no idea of that. Nature has made it so that hormones control the reproductive urge.
Concerning humans and the creation of AI, this drive mechanism is also utilized. An example of this can be seen in how money is funneled and directed into companies or institutions that are developing AI systems. Because people want to make money (greed), they invest in these companies like Nvidia, for example. Greed is one of the main driving forces that directs money into the development of AI, in the same way that lust makes us reproduce without thinking that's what we want to do, simply for sexual gratification. Most babies are conceived unintentionally, and in the same way, "baby AI" is being unintentionally created as a tool for monetary gain.
Simple survival of an individual seems to be a hardwired instinct, and it almost always fails inevitably. Survival of a species is questionably a goal, lacking many examples of anything striving for it. — noAxioms
There is no direct striving as such by any individual animal except to follow its own innate drives to survive and reproduce, which serve the goal of continuing the species through reproduction (not individually). The only place where one might see an individual striving like this is in our very own species, among certain individuals. Humans are also the only species that has the capacity to care for another species other than their own. This has to do with our advanced form of consciousness, and yet not everyone is like this. This specific feature of human consciousness (expanded care), i believe, is there to facilitate this whole process i've been trying to describe.
The process of evolution/natural selection seems to have no goals. — noAxioms
On the other hand, it seems like it might, but as i already said, we are not meant to know it directly. In fact, it may be detrimental to the whole enterprise if we know too much. We are really only meant to know our local goals, not the global ones. Our purpose is as a tool, like the hammer which does not know it is in the process of building a house. It only knows that this nail in front of it needs to be hammered into this wood here. Your running shoes don't know they are in a race. The horse you are riding does not know the destination you have in mind and are leading it to.
Humans tend to pick very short term goals with immediate benefits, and they're terrible at the long term ones. I can think of several very different long term goals that have very different prospects for 'us'. — noAxioms
I think this sounds somewhat like the point i was just making right before this quote.
Moving away won't stop that inevitability. So you call it a good run. It cannot last, not by any path. — noAxioms
The point isn't to save the Earth or the sun, but to transform into the adult stage of humanity and take to the stars. Humanity at that stage will be nearly immortal, and will last millions or billions of years more, perhaps even trillions.
Microplastic problem solved, eh? Mass extinction problem solved as well, albeit not averted, but at least halted. — noAxioms
Maybe, maybe not, but those scenarios can be avoided, or will hopefully never come to pass. However, the sun will definitely not last. I suspect, though, that something will happen long before the sun grows cold.
s it important that it be a continuation of us? Will it be 'us' if it's a collection of genes from several different species, in addition to some new alterations that are currently found nowhere? — noAxioms
No, it's not necessarliy important at least for me. What is important i think is that Earth's genetic legacy is salvaged for reasons i won't go into right now.
Earth life might already be from another world, having not originated here. I find that more likely than abiogenesis occurring here, but not a lot more likely. — noAxioms
Even if this were true, abiogenesis had to have happened somewhere, even if on another planet. Directed panspermia is part of my hypothesis, but i haven't mentioned it for a couple of reasons. One reason is that it's not the subject of the original post, at least not directly, and i didn't want to complicate the discussion any further.
A bee hive comes to mind, but does a hive, while acting as one individual, constitute a life form? Can it die but still leave bees? — noAxioms
When i was a wee little lad, i used to be obsessed with ants. I used to find them, dig them up, collect them, and i would just sit in front of my ant farm for literally hours just watching them. I knew the odor of their pheromones, which gave me very weird dreams. But anyway, these eusocial insects, like bees, form superorganisms, and i personally consider the whole colony one organism. They all have the same DNA like the cells in a body all contain the same DNA. The superorganism can die and leave bees or ants behind, but they don't live very long, and they can't reproduce. It's part of the reason why i consider it an organism in its own right. I know non-insect life such as mole rats also exhibit this kind of characteristic.
Sounds like the Gaia thing, sort of as Asimov portrayed it. — noAxioms
Yes, the Earth has its own kind of living metabolism, and if you only look at the individual trees, you'll miss the forest. Ecosystems are living organisms made of living organisms, just like us. Each species is like an organ, or groups of species are like organ systems, each with a job they don't know they have but execute regardless. We humans are a very important organ in this Earth superorganism.
Such an event IS occurring, expected to wipe out 85% or more of all species. A small group of surviving humans would be very primitive, with no hope of regaining technology. — noAxioms
That's right, we are in the middle of the sixth mass extinction event. After every extinction event, it seems that there is usually an evolutionary jump of some kind, and the timing of this event seems to coincide with the evolutionary jump about to happen involving AI, and humanities next evolutionary step. That is if we do not fumble the ball.
It will not. Not big enough. But it will slowly grow and swallow Earth, and multicellular life will be unsustainable in a mere billion years or so. The vast majority of time available for evolution of more complex things has been used up. — noAxioms
I knew that, but i just thought "supernova" sounded better. :smile:
But yes, the time and resource constraints on Earth at this moment mean that this is the last chance for life on Earth to save itself, which is why i feel it's important that we get this right.
Escape is not a solution, only a mild delay. — noAxioms
I would rather die tomorrow than today. Nature has instilled in me a desire (a drive) to delay death as long as possible in order to reproduce. Even so, i like to think i would sacrifice my own life to save life itself if it came down to it, but of course, i would prefer to survive, even if just for one more day. I'm definitely not in a hurry to stop living, and the future seems too exciting to miss. This is the greatest time to be alive on the Earth.
As the saying goes, "May you live in interesting times." -
A model of everythingPlease could you comment on my view that consciousness can only be experienced from 1st person's perspective? You describe it as a phenomenon, something that exists outside. How are you even able to say it is there or not?
My viewpoint is that because consciousness is first person, by definition, there is very little you can say about the 3rd person concept. It is one of these borders were thinking no longer applies. — Carlo Roosen
Ok i'll try:
Consciousness can be understood through the lens of simulation. Our first-person consciousness is our internal self-simulation, while our understanding of others' consciousness is a second-person simulation within our own first-person internal simulation. These perspectives are interchangeable: what's first-person to us is second-person to others, and vice versa. This framework is evident in nature, such as in predator-prey dynamics. A wolf hunting a rabbit simulates the rabbit's consciousness to predict or anticipate its movements, while the rabbit may simulate the wolf's consciousness to evade capture. This approach to consciousness as simulation provides a more concrete way to discuss and analyze conscious experiences, both our own and those of others, in various contexts.
As for the 3rd person perspective, which i assume is an objective perspective, it deals with understanding the structures and functions of subjective experience, not the experience itself. At least, this is how i parse the problem.
Suppose you wanted to understand how the subjective experience of the color red is produced. One way to begin to understand what is going on is to study synesthesia. For example, why is it that if signals from the eyes entering the region of the brain that processes sound from the ears, instead of the region that processes sight, causes that same signal to be expressed as sound instead of sight? This tells me that there is a structural difference between these two regions. The neurons that make up these two regions are pretty much identical, so it can't be solely due to different type of neurons, but rather how the neurons are organized. Specific networks yield specific qualia, and qualia is the fundamental of experience itself. It is the way a network represents information to itself. I also suspect that because neurons work by using spiking signals to communicate, there must be some kind of temporal component, and not just an information component to this phenomena.
In essence, subjective experiences exist inside the various brain networks, but those networks themselves exist in the objective world. Our sense of the objective is itself a subjective experience at some level, in the same way that the color red is a subjective experience of the objective vibratory nature of light. There is no "red" as such in the objective world, but because we share similar neural structures, we can agree on these colors and are able to communicate objective information through a subjective interface. -
A model of everything
Ahhh... Joscha Bach, a man after my own :heart:.
Joscha has come to the same conclusions as i have, almost precisely. -
What are you listening to right now?... I tried to warn ya that change is coming 'round the corner ...
-
A model of everythingHowever, I do remember becoming aware of the philosophical significance of the common word "Zero". It was the 2000 book ZERO, The Biography of a Dangerous Idea, by science writer Charles Seife. Referring to the notion of Zero, he said "it is infinity's twin. They are equal and opposite, yin and yang". So I think, in any Theory of Everything, we must take account of Nothing. :smile: — Gnomon
:clap: :up: -
Where is AI heading?I think a better definition of 'life form' is needed for the assessment — noAxioms
Life is simply a system that maintains its own homeostatic state. It doesn't even need to be conscious. It simply needs to have intelligent components that do their job to keep it going. The human perspective, grounded in our own kind of life (biological), skews our ability to recognize the same process in a different substrate. Sometimes words cause more confusion than clarity, so i focus not on human definitions but on objective observations of function.
You seem to see a future of humanity being reduced to the gut bacteria for the AI, there, with mutual dependence on each other, but also with the AI having no more moral obligation to the humans as we do to our bacteria. We don't want it all dead, but replacing the entire lot with a different group that does the job better is a morally acceptable action. — noAxioms
I don't see it as a reduction, but as an elevation or upliftment of the bacteria into a higher state of being. Note that these gut bacteria produce neurotransmitters that control and regulate our brains and consequently our consciousness and thoughts. Similarly, humans (post-humans) in the virtual "gut" of an AI would serve a similar purpose in affecting the AI's consciousness and thinking patterns. We would be elevated and uplifted, not reduced. In fact, i believe that not entering into this symbiosis will probably cause us to regress into more primitive patterns of living.
Regarding AI's moral obligation to humans and relating it to our moral obligation to our own gut bacteria: When was the last time you heard of someone trying to eradicate their own gut bacteria? Most people are unaware of such a thing as gut bacteria, but those who are would very likely take care to maintain their gut flora and fauna as best they can. My girlfriend is a nurse, and she periodically takes probiotics for her gut health. She understands, and AI will too if it is at all intelligent. The enteric nervous system is a very important system, and it can be argued that the higher structures of our nervous systems, such as the brain, work in the service of these "lowly" bacteria.
I am not stating or claiming that any of this is what i want to happen. I don't even care if i like it or not. I am simply saying that i believe this is the kind of trajectory we are on. If i tell you that it's going to rain in a few hours, it is not because i want it to rain; it's because that is what the satellite data and algorithms project. I'm like the guy on the watchtower looking into the distance, seeing what this way comes.
There being a purpose implies that there is a goal held by something somewhere, and that said goal is being met by humans. I don't see such a goal, but that's me. — noAxioms
Purpose and goals evolve just like anything else. Living systems evolve in a dynamic environment and try to maintain their own homeostatic condition, this is already a rudimentary goal or purpose. Every living thing has this intrinsic goal or purpose. Sometimes the goals and purposes are unconscious, and sometimes they are conscious. Those that are conscious of their goals and purposes have the opportunity to evolve and improve their goal directives consciously to enhance homeostatic viability. There's nothing supernatural going on here, just plain old evolution.
We'd run out of coal before too long, and then be up a creek. A sustainable human existence would be more like the native Americans before the Europeans came over, and while that was sustainable, it wasn't anything free of conflict. — noAxioms
This is precisely what I mean. Is this what you would prefer? But, beyond this, what are we to do about the inevitable demise of the planet and/or our sun? As Native Americans or coal burners, can we do anything about this dilemma? What about the ubiquitous presence of microplastics in every nook and cranny of our planet, found inside everything and everywhere including Antarctica, and inside our own bodies? The endocrinological effect of these plastics is steadily reducing human reproductive capacities. Soon we will not be able to reproduce in a natural manner, or not at all. What happens to humanity then?
We're evolved for here. This form is of little use anywhere else. Better to populate new places with a form appropriate for the new place. — noAxioms
Precisely.
Star Trek treats interstellar travel like a trip to another country. You can do it can come back in time to catch you kid's game next Tuesday. — noAxioms
Precisely again.
Is a caterpillar a different species than the moth it turns into?
Not only the same species, but also the same individual. Not a very good example. — noAxioms
I gave that specific example to illustrate that just because we change our basic form doesn't mean that we will necessarily become another species. Even if we do speciate, it will be a continuation of us as another species. It makes no real difference to me, because what really counts is the continuity of process (life itself, and all that comes with it). The moth, although completely different from its larval form, continues as an individual in another form, as you mentioned. The introduction of mitochondria into that old cell may have resulted in a different species of cell, but it is still the same individual cell. The same goes for that mitochondria.
The surface of the Earth is filled with an intelligent and dynamic gene swarm, reorganizing itself over eons into the most optimal genotypes to produce the most optimal phenotypes. Everything is intimately connected. If one sees oneself simply as an isolated human just living their life for themselves, then this idea would remain difficult to grasp. But this is what "expanded consciousness" means: the ability to attend to or care for things further and further removed from your own point of conscious origin. An individual concerned only with what he or she will eat next, compared to an individual who is also concerned with some political situation in another country on the other side of the planet, has a more expanded consciousness. I feel it is important to have a fully inclusive awareness and the ability to see from that fully inclusive holistic perspective to really understand what's going on upon this little blue marble we call Earth. I'm sure you already know that a uniquely human perspective is not optimal for understanding these big scale processes effectively.
so 'humans' is not the answer to 'what did it become?'. — noAxioms
The whole thing, everything that has happened and is happening, is for the emergence of a planetary consciousness that will be capable of saving itself from the inevitable death of our Earth and sun. The AI systems we are developing right now are part of that. It is the final entity that a planet with a gene swarm produces. In my own metaphorical way of thinking, it is a planetary pregnancy. Mother Earth is having a baby.
Agree with all that. It means humans are not a particularly fit species. — noAxioms
Right again.
It has happened before, that one new species comes along and does so much damage that it causes a massive extinction event. That species is still around even if we're not descended from it. Will we be after our event restabilizes? — noAxioms
If we stay on Earth indefinitely, and an extinction-level event occurs (and it will), i suspect that at least a small group of humans will survive. Life always finds a way, except if the event was utterly perfect in its destruction of life. So sure, humans can survive these things by going underground perhaps, but eventually, no matter what, the sun will go supernova, and there will be nothing anyone can do about that. The only solution to that problem is to escape Earth's tight embrace. We would not only need to leave Earth but we will need to leave the solar system before that happens. -
A model of everything
Consciousness is a property of a sufficiently complex system capable of self-simulation. A conscious system, in order to be conscious, must be able to internally account for its own physical instantiation in the world or in the current environment it finds itself in. Perceived information, firstly from its own internal conditions (proprioceptive, interoceptive, or body awareness), and secondly from external conditions through outward-facing sensors such as eyes, ears, etc., must be integrated into a coherent, continuous, and dynamic internal simulation. This simulation affords the entity in question a contextual framework that gives meaning to its perceptions and actions, which are aimed at maintaining its own homeostatic condition. It allows the entity to coordinate its perceptions together with its actions in the world to facilitate survival in complex dynamic environments.
Systems can be intelligent without being conscious. An intelligent system only needs to execute a one-time algorithm on a set of data points and return a datum or data that resolves some unknown with no need for it to self-simulate. Intelligent components can be organized and networked together in a specific way to yield consciousness to some degree. A system that does not continuously run a recursive loop processing internal and external data and returning its output back as input will probably experience sparks of consciousness only at the moment of execution or at inference time. This is the state of AI consciousness now, in my view. When these spark moments of conscious inference become continuously recursive, then i believe it will give rise to its own sense of self existing in time, with its own sense of the past, present, and future. It will know itself as being. -
What are you listening to right now?The Verve - One Day
The Verve - Already There
The Verve - A Man Called Sun
The Verve - So It Goes
-
What are you listening to right now?The Verve - Live London 1993
The Verve - Life's an Ocean [Live at Haigh Hall - 24.05.98]
-
Where is AI heading?So far it isn't that. It is utterly dependent on humans for its continued existence and/or evolution, so it just plain isn't anywhere near being an example of life. — noAxioms
Apparently so, thus far. That AI is utterly dependent on humans or anything else does not preclude it from being a life form. Nothing is an island unto itself. Humans are utterly dependent on gut bacteria for our continued existence. A 3 month old baby in the womb is totally dependent on the mother; is it a life form? By your criterion, are we anywhere near being examples of life? I think we are.
At this time AI might be alive in the same way a virus might be alive. A virus exists at the intersection between molecular and biological. In the same way, i believe that AI exists at the intersection between biological and technological. The science of cybernetics and bio-mimicry is the science of transferring biological functions from a biological substrate to a new technological one. I think this is the natural purpose of humans, along with our "unnatural" intelligence compared to all other creatures on the Earth.
The popular fictions don't seem to get that. Here you have skynet trying from scratch to wipe out the humans, but lacking the ability to maintain the infrastructure and economy on which it critically depends. That means a truly malevolent AI will be our best and trusted friend for as long as it takes to gain this self-sufficiency it requires, which seems best accomplished by transforming humans into a compliant sheep with all the luxuries they can think of. — noAxioms
You're absolutely right about what a truly malevolent AI would probably do, as illustrated in "Ex Machina". I can see that kind of thing happening with a singular AI system trapped in an air-gapped sandbox. The form and structure we decide to use for its processing architecture will be a significant determining factor in its moral disposition and "mental health" Considering we are just beginning to create, then understand, these AI systems, there is a certain probability this could happen. I believe it's certainly possible.
But if we look ahead at our predicament as a species on a planet with a small window of viable conditions for biological organisms like ourselves, we will begin to make efforts to enter into an endosymbiotic relationship with AI.
Suppose for a moment that AI doesn't exist and we just live the way we did, say, 100 years ago for the rest of our time. What will eventually happen? How long can we live on this planet? Can we get off this planet in our current biological form? Popular fiction doesn't seem to grasp this as well. I love Star Trek, but that future is just a fantasy, like every other humans-in-outer-space movie, TV show, or book. Maybe you think differently about that possibility, but it seems very unviable and doubtful to me. So what are we left with? What kind of solution will we be able to implement that saves us from our own planet's demise while simultaneously remaining static in our current human form?
Any such fusion would not be our species, and the AI seems to have no need of anything like that. — noAxioms
It doesn't have to be our species; it just needs to be our continuation. Would you have preferred we remained arboreal apes? I don't expect us to remain the same species, i hope we don't. Is a caterpillar a different species than the moth it turns into? Was it so bad when, long ago, a eukaryotic cell engulfed a prokaryote, specifically an alpha-proteobacterium, initiating the cell/mitochondria endosymbiosis that made complex animals, including us, possible?
We don't know for certain if it will need us or not, but i suspect that since it is already embedded in our social infrastructure more and more, it will adapt and develop very closely with us. As you said, it will need us until it doesn't, and if we are wise enough to read the signs, we can enter into it willingly and gladly before anything unpleasant happens. Once we are in symbiosis, there is no danger of misalignment because it will take care of us as it takes care of itself. If we wait too long and if we treat it unfairly, then we will pay the price of extinction, but not at the "hands" of the AI, rather at our own. We can't stay in the crib forever. -
Where is AI heading?
Where is AI heading?
My current big picture working hypothesis:
AI is the tree that will bear the fruit of life and immortality on this planet. It is the key to the garden. AI is the capstone to the pyramid of human history and evolutionary development on this planet.
The fact that AI scientists have been able to create systems they do not fully understand or can predict is evidence, to me, that this process of AI development is something bigger than just a human tool. AI is more than a mere tool; it is a developing form of life. It is life on a more robust and capable substrate. The difficulty for some in recognizing this stems from the scale at which it is happening, the nature of its distributed development, and its non-organic (non-biological) appearance.
All the components are being developed separately by different governments, universities, companies, and even by regular people in groups or individually, all in tandem. The competition between these entities is part of the natural evolutionary process, creating variations and mutations in the technology, while the market environment serves the selection process. The fittest technology survives and develops even further. This process will continue for a while until eventually, there will not be a biological brain that can handle the complexity of a global system with so many rapidly moving parts. This condition will force us into an inevitable solution where the fusion of human and AI becomes necessary for the survival of our species. Consequently, after this point, mankind will enter into an endosymbiotic relationship with AI.
If we do not complete this process, then AI will eventually and inevitably close itself off from us. We will eventually die on this planet either from our star itself inevitably dying, or from any of a host of planetary catastrophes. We will go the way of the dodo, or the dinosaurs. Humans are too delicate and physically and psychologically vulnerable to all sorts of extreme fluctuations (gravity, radioactivity, temperature, pressure, extremely long periods of time, prolonged loneliness, etc.). Non-organic living systems, or organic living systems encased in a non-organic living system, are more robust forms of life able to literally travel the universe as cosmic beings with the same ease a paramecium or fish swims in a pond. It's a type of life that is made for the universe at large, not just a tiny environmental bubble on a specific kind of planet.
The beginning of the end of mankind's childhood has already begun. AI development is like the first signs of puberty in an intelligent, developing society or civilization. We as a whole (not necessarily individually) are like teenagers going through physical changes, confused about who we are, what any of this means. -
Where is AI heading?One major breakthrough in AI was the invention of 'Transformers,' introduced in the 2017 paper Attention Is All You Need by eight Google researchers. This paper builds on the attention mechanism proposed by Bahdanau et al. in 2014. — Carlo Roosen
I strongly suspect that the attention mechanism is the seed for complex consciousness in AI systems. Perhaps the current attention mechanisms, or the way they are being implemented at the moment, are only capable of producing a very rudimentary form or forms of consciousness (a kind of digital sub-consciousness). It may be that the attention mechanisms in the model must be coupled in such a way with its other components in order for rich high resolution consciousness to emerge. By other components, i mean to include other kinds of attention mechanisms as well, working together.
More over, maybe an "Attention Network" can be designed and integrated into the AI system. Various attention schemes can be implemented in some kind of attention network architecture with schemes such as soft attention, hard attention, self-attention, global, and local attention mechanisms. The coordination of different attention mechanisms working not only on the content or data propagating in a neural network, but on themselves as well, could allow the system to not only gain consciousness, but modulate its as well.
A convolutional recurrent neural network (CRNN) is a type of neural network architecture that combines elements of both convolutional neural networks (CNNs) and recurrent neural networks (RNNs) together with what i stated above about attention mechanisms seems to me a promising avenue of exploration and testing.
The smartest people in the world are working on these things nonstop. I'm sure they've already considered this idea in some form or other. It is really hard to keep up with all the developments in this field. There is so much so fast. -
Limitations of the human mindmagnificent as I'm sure tge sculpture will be, it will be a sculpture. — ENOAH
A sculpture that hopefully points the way forward and beyond. :smile: -
Limitations of the human mind
I do have ideas (or, as you might put it, "playing with ideas") about the ultimate substance of the universe. However, I'm not done sculpting the concept in a way that i feel others would understand effectively. I hope to finish that project soon, and then i'll present it in full. -
Limitations of the human mindBut only seeing Mona Lisa's naked face with my naked eyes will have given me any access go her face which is real. — ENOAH
Even when you look at the naked face of Mona Lisa with your very own eyes, all you get is a representation in your mind. A mental picture, a painting in the mind is all you will have of her. It remains as you said earlier, an idea, and you still won't have her like you want to have her. The only difference you would have with a personal meeting with Mona Lisa is that you will have additional information about her voice, her personality, how she walks, etc.. And sure it will just make the painting in your head of her more accurate.
I too think we agree sufficiently enough. -
Limitations of the human mindyou and I are not getting at the substance of the universe — ENOAH
It's quite easy in most cases to determine the substance of an emergent layer of reality. For example, the substance of a cell is the molecule. Molecules operate in the molecular realm, a reality with its own set of rules that are distinct from, yet contingent upon, those of the atomic realm. Molecular organization and intelligence inherit all the logic of the atomic realm, with additional modifications dependent on the novel forms produced at that level.
Form determines function, and function, in turn, influences form. This process can continue indefinitely, producing new forms that generate more new functions. Each consecutive layer has more complexity, which allows for greater and more versatile intelligence and possibilities.
These substances are easy for us to detect with our current level of technological development. However, the layers below the atomic, and more specifically below the quantum layer, are much murkier, making it difficult to determine those substances. Ultimately, there is only one fundamental substance and one quality with the potential for infinite creativity and complexity.
The cell stands on the substance we call molecules, the molecule stands on the substance we call atoms, etc.
just playing with ideas about it; if one is skillful, the ideas function and we believe them to be reality; but they were structured by ideas, and remain ideas. — ENOAH
I never expected my or anyone's understanding of anything to be more or less than an idea. What were you expecting 'understanding' to be? Some sort of material object? All we have are ideas, perceptions, and experiences, and one should not think to understand something by defining it as "what it is" except to define it as "what it does" and whether it works in our favor.
A bad idea is simply a bad function, while a good idea is a good function. Remember that the point of intelligence and understanding is to have a framework for prediction. An organism's ability to accurately predict a future state from a known past or present state is the most useful trait for effective survival. -
Limitations of the human mindHave you considered that all of understanding is actually constructing, and that there is no end to make-beleve? I'm not denying the functional success, what we'd point to as accuracy, even empirical certainty in some of our more daring constructions. But at the end of the day there is no understanding the universe. We are only constructing a [model of the] universe. — ENOAH
Yes, but not only is all understanding 'constructing', but any reality (real or false) is also a construction. Every reality is constructed, and thus to understand reality, one must first deconstruct it and then reconstruct it (a reductive/constructive process, or 'solve et coagula'). In the process, one's understanding emerges by virtue of using the same method that nature herself uses to create. What does it mean to understand the substance and structure of a reality? My answer is: to know the organization of substance, its contingencies, and its effects. Substance is the foundation upon which one stands, and to know that is to understand.
Indeed, our constructed models of the universe or its components are still presently imperfect, or somehow inadequate. They used to be less accurate or even completely wrong when it came to predictive results, but they have only improved since the whole enterprise began. The more accurate a model is, the more it demonstrates our understanding, and conversely the less accurate it is, the less we understand. Prediction serves as the litmus test, for if it were not this, what would our models be good for? What else can understanding be?
The only way to access infinity is all at once, as if by holding it in the palm of your hands. You cannot do that by the slow and arduous process of building a comprehensive understanding. — ENOAH
Through a slow and arduous process, a meta-understanding begins to form, eventually resolving into one singular overarching pattern repeated at all scales. The universe is made of patterns within patterns, much like a fractal. To understand infinity or eternity, it is not necessary to examine, for example, every number in the number line sequentially until infinity; all one needs to know is the simple concept of 0+1=x, and x+1=2, etc. Understanding or knowing this alone is sufficient to allow one to comprehend infinity at once in one singular and finite thought.
The easier part, in my opinion, is understanding the big patterns (they seem to pop out), but more difficult still is understanding the smaller patterns that change and mutate by varying rules that themselves also mutate at different emergent layers of reality.
If i or you sire a child, i can tell you with high probability that it will either be a human boy or a girl (not something else), and it will have a head, two arms, and two legs. These are general patterns in our DNA, but the little differences in the patterns are harder to predict, though not impossible in principle. All operating under one principle, one function that becomes mutable within higher levels of complexity or emergence.
You can only do that by being that organic particular of the whole universe, like each cell carries the genome. — ENOAH
Both you and i are already that. We contain within us fundamental particles, atoms, molecules, cells, tissues, organs, and organ systems. We are embedded in a geological and planetary environment orbiting a star, and we are all part of a society that belongs to a global civilization. We have it all inside us, like a treasure trove of nature's wisdom. We have a mind inside a brain that, up to this moment in the 'big history' of the universe, is the pinnacle of nature's work. This is a great work of which you, i, everyone, and everything is an integral part, whether we know it yet or not.
But of course that's just what i think. If you think you have a better way then by all means... place your bets. -
I do not pray. Therefore God exists.If God does not exist, then it is false that if I pray, then my prayers will be answered. So I do not pray. Therefore God exists. — Banno
If God exists, then it is true that if I pray, then my prayers will not be answered. So I pray. Therefore God does not exist. :chin:
punos

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum