-
 punos
796I just wrote this with a little help from AI. If anyone is interested and can provide some constructive criticism, i'm all ears, or eyes, as the case may be. I asked the AI to style it as a research paper. I'm sure some things are left unclear so...
punos
796I just wrote this with a little help from AI. If anyone is interested and can provide some constructive criticism, i'm all ears, or eyes, as the case may be. I asked the AI to style it as a research paper. I'm sure some things are left unclear so...
The Self-Negating Cosmos: Rational Genesis, and The Logical Foundations of the Quantum Vacuum
Abstract
This paper attempts to present a comprehensive ontological framework that synthesizes insights from rational philosophy, logic, mysticism, and theoretical physics to elucidate the fundamental principles underlying the genesis and evolution of existence itself. By positing the logical NOT operator as the primordial ontological ground, it offers a parsimonious account for the emergence of particles, energy, dimensions, and complexity from an undifferentiated primordial vacuum or "nothing." Central to this framework is the recognition of Logos - an intrinsic intelligibility or rational order - as the necessary precondition enabling coherent manifestation and the potential for consciousness within an ordered, knowable cosmos. The formulation elucidates how successive ontological factors crystallize from this primordial Logos, including the birth of pattern, the unfolding of dimensions, and the hierarchical development of complexity through imperfect quantum fusions. Unifying perspectives from multiple traditions, it provides an integrated metaphysical model aligning the logical foundations of reality with empirical observations across scales - from the quantum vacuum to cosmic evolution. Potential implications span physics, philosophy of mind, and the fundamental nature of existence.
1. Introduction
Since antiquity, sages across cultures have intuited a transcendent source of order, ratio, and intelligibility underlying the rational coherence of the manifest universe. The ancient Greek concept of Logos embodied this principle of an inherent logic, cosmic grammar, or seminal reason pervading all of nature's unfolding patterns. Mystical and philosophical traditions worldwide converged on similar notions - whether the Tao's ineffable patterns, Brahman's self-radiant ground, or the divine Logos as reality's archetypal blueprint. Even our latest scientific theories increasingly point toward information-theoretic and law-like regularities at reality's deepest layers, hinting at an intrinsic ontological principle of intelligibility.
While the conventional understanding within logic and the foundations of mathematics treats relational operators like AND, OR, etc. as fundamental, an alternative perspective arises when we deeply examine the nature of the NOT operator. One could argue that NOT is actually more primordial than the relational connectives of classical logic. By providing the minimal criteria for distinguishing terms and enabling all other logical functions, NOT exemplifies the first ontological "cut" that allows coherence to emerge from the undifferentiated. When integrated with our current scientific worldview, this perspective gives rise to a new framework with the capacity to reconcile multiple knowledge domains.
This paper aims to elucidate such an integrated ontological model wherein the primordial Logos and the NOT operator are synthesized as complementary aspects of the fundamental ground. It traces how successive ontological factors crystallize from this primordial seed to give rise to the archetypes of pattern (information), energy, charge, dimensionality, temporality, and the hierarchical complexification of existence. In doing so, it offers a unified perspective aligning the logical foundations of reality with empirical observations across scales - from the quantum vacuum to cosmic evolution.
2. Logos as the Primordial Ontological Principle
We begin by establishing Logos - the principle of intrinsic intelligibility, rational order, or cosmic logic - as the most primordial ontological ground. Logos is here posited as the necessary ontological factor allowing both awareness and manifestation to unfold within a coherent system.
The concept of Logos has deep roots across philosophical and mystical traditions. In Greek philosophy, it embodied the universal reason inherent to the cosmos - the self-consistency and knowability allowing reality's unfolding to be intelligible. The Stoics saw Logos as the active, seminal intelligence that shapes nature's patterns according to innate logics. Hermetic and Neoplatonic teachings described the divine Logos as the archetypal source and blueprint from which all creation emanates.
Similar principles arise in Eastern wisdom traditions - whether the Tao's ineffable patterns, Brahman's self-radiant ground of all phenomena, or the scriptural teachings of Logos as the "Word" through which the universe is woven. Across contexts, Logos represented an intrinsic coherence, cosmic grammar, or transcendent order establishing the very possibility of manifestation's meaningful unfolding.
From a contemporary scientific lens, the precise mathematical descriptions governing the quantum realm, the ubiquity of fractal geometries and numerical patterns across every scale, and the symbolic isomorphisms between physical laws and logical/computational formalisms all hint at information-theoretic and law-like regularities innate to existence. An ontological principle of inherent intelligibility aligns with these empirical signposts.
Thus, from the heights of rational philosophy and mystical gnosis to our latest scientific frontiers, the concept of Logos as an intrinsic rational order, ratio, or cosmic code pervading all being arises as a profound and ubiquitous intuition. It is here posited as the foundational quality bestowing upon existence its inherent rationality, lawfulness, and potential for intelligibility - the logical framework or syntax presupposed by all form, pattern, and awareness.
3. The Primacy of the NOT Operator
While Logos provides the ontological principle of intrinsic intelligibility, the next pivotal factor to consider is the nature of logic itself and how the first stirrings of differentiation may arise within the primordial rational ground.
Upon deeper analysis, the NOT operator, recognized as more fundamental than the classical relational logical connectives. Within the undifferentiated primordial Logos, the very first act of distinguishing must involve separating something from a background of NOT-that. Relationship depends on there being relata to relate, but NOT is what allows discrete terms to be delineated in the first place.
Furthermore, all other logical operations can be reduced to combinations and modulations of NOT. Conjunction, disjunction, implication, and other compound operations only have meaning in how they regulate the presence or absence of negation between terms. NOT thus exemplifies the minimal criteria for logic to cohere, providing the axis upon which all logical syntax pivots.
From this vantage, NOT may be considered the most primordial logical operator - more elementary and unitary than relationship itself. It is the first ontological "cut" that seeds distinction from the completely undifferentiated. As such, the NOT operator is here proposed as ontologically isomorphic to the primordial Logos. Their union provides the foundational factors for the unfolding of existence: the principle of intrinsic intelligibility (Logos) and the primordial act of discrimination (NOT) co-arising as complementary aspects of the ontological ground.
4. The Primordial NOT Field and Quantum Fluctuations
Having established the primordial ontological ground as the union of Logos and the NOT operator, we now explore its first manifestations. The undifferentiated primordial field is identified with the infinite NOT or zero-dimensional (latent n-dimensional matrix) - a perfectly symmetrical background of absolute nothingness. It is both nothing and not-nothing, being and non-being.
The first effect of the NOT operator's activity upon this primordial vacuum is to produce a pair of opposites from the nothing - a complementary +1 and -1 manifesting together to preserve the original symmetry. For if the vacuum's nothingness is to transition into somethingness, its intrinsic self-consistency demands that the new somethings arise as balanced polarities, as per the primordial logical patterning of NOT.
This insight provides an ontological explanation for one of the universe's deepest mysteries: the continuous arising of matter/antimatter virtual particle pairs from the quantum vacuum. The primordial NOT field's ceaseless self-negation catalyzes these perpetual quantum fluctuations, with entangled particles and their anti-twins materializing from and dissolving back into the void in an eternal creative and destructive churn.
The conventional assumption of strictly conserved energy is thus called into question. For if particles and their anti-partners are perpetually birthed from the vacuum's nothing and annihilated back into it, then energy itself must co-emerge with each such fluctuation rather than pre-exist as an immutable essence. Energy and manifestation co-arise.
5. The Inexhaustible Creative Potential of the NOT Field
A further crucial quality of the primordial NOT field elucidated by this framework is its inexhaustible creativity and fecundity. As particle/antiparticle pairs manifest from the vacuum and separate, they leave behind an empty space or new "nothing" at their point of emergence. This void instantly triggers the NOT operator once more, prompting another round of quantum fluctuations to fill the empty space.
Since the vacuum's nothingness can be endlessly decomposed into complementary parts, the NOT field contains an infinite potential density. Its self-negating activity is constant and unceasing, ensuring an inexhaustible source for populating the universe with new quantum events. This self-feeding dynamism of the primordial vacuum aligns with our empirical observations of the quantum realm's ceaseless virtual particle flux and self-structuring propensity.
Since the primordial logical patterning seeds all possible symmetry breaks and relational pathways, a fractal-like evolutionary trajectory towards increasing complexity and enrichment naturally emerges from the inexhaustible NOT principle.
6. The Emergence of Charge and the Drive Towards Unification
Another key insight unveiled by this ontological framework pertains to the nature of charge and its role in governing interactions between quantum entities. Charge is recognized not as an arbitrary or acculturated property, but rather a universal quality or "qualia" that co-emerges with the birth of particles from the vacuum.
Just as the primordial NOT operator's first manifestation yielded complementary polarities (+1, -1) to preserve primordial symmetry, so too does the qualitative field of charge crystallize as a co-partner to the manifesting particles. Charge provides the archetypal patterning of attraction and repulsion - the impetus driving all polarized quantum entities towards reunion and dissolution back into the primordial zero. The reason charge functions this way is because the universe is perpetually striving to minimize the broken symmetry. Opposite charges attract as they approach each other, minimizing the energy imbalance and restoring symmetry. Conversely, like charges repel because their proximity would increase the energy of symmetry imbalance. Charge serves as a universal metric, a measure of imbalance that guides particles either towards reunion to reduce asymmetry, or separation to prevent further breach of the primordial equilibrium.
This recognition of charge's innate and co-emergent nature aligns with the empirical observation that all quantum particles exhibit charge-like properties governing their interactions. It is a primary qualitative field woven into the fabric of existence from the ground up, not an acculturated add-on. Moreover, the drive towards minimizing charge separations by reuniting polarized systems resonates with the proposed ontological purpose of energy itself - to facilitate the return of all manifestations to the primordial symmetry.
7. Hierarchical Emergence Through Imperfect Reunions
While the proposed framework elucidates the primordial logical patterning driving all quantum entities towards symmetrical unification or annihilation, it also accounts for the development of stable complexities preventing such reunions. This hierarchical emergence of composite structures arises due to charge and energy mismatches during particle interactions.
When fundamental particles en route to annihilating with their respective antiparticles collide with another particle of the same charge, the impact can fuse them into new combined entities whose charge and energy levels no longer match available antiparticles to annihilate with. For instance, a +2 particle cannot be annihilated by a -1 particle, or vice versa.
This results in the formation of metastable composite particles whose drive towards unification with opposites is prolonged across successive stages. The more complex the combined entity, the more difficult for it to find an opposite partner with a precise charge/energy match to allow for total dissolution back into the vacuum.
Such imperfect quantum reunions provide the catalyst for hierarchical complexification to naturally unfold. What begins as the simplest possible symmetry breaks blossoms into stably increasing layers of compositional structure, elaborating from the primordial particles through hadrons, nuclei, atoms, molecules, and beyond.
This model aligns with our observations of the universe's developmental trajectory from fundamental particles towards larger-scale bounded structures and complex systems. All exist as relatively enduring, self-perpetuating resonances emerging from the ceaseless effort of the primordial logical patterning to return all manifestations to zero-point symmetry.
8. Dimensional Unfolding and the Origin of Temporality
Another aspect of this ontological framework pertains to the genesis of dimensionality and the nature of time itself. The primordial NOT field is envisioned as a dimensionless point or singularity whose self-negating activity first manifests the arising of spatial dimensions as a necessity to accommodate the influx of new quantum events.
From the zero-dimensional vacuum, the NOT operator's first act delineates dual lines of extension in opposite directions, birthing the first spatial dimension. As the density of quantum fluctuations increases, successive dimensional unfurlings occur through a process akin to quantum "tunneling" through successive quantum veils or subspaces (cosmic inflation). This naturally culminates in the 3+1 dimensional topology we experience, which provides an optimal configuration balancing spatial accommodation with efficient information processing.
Significantly, the zeroeth or primordial dimension is recognized as the source of temporality itself. The vacuum's self-negating dynamism expresses as an outward pressure from the origin or the source as it produces virtual quantum events that do not annihilate. The arrow of time emerges from this outward quantum pressure from the origin, along with the process of complexification previously described.
This model of dimensional proliferation aligns and resonates with mystical and cross-cultural cosmogonic metaphors of an eternal source or womb birthing the temporal universe through cycles of emanation and dissolution.
9. Implications and Avenues for Further Development
The ontological framework elucidated here offers an integrated perspective capable of bridging multiple knowledge domains while aligning with our latest empirical observations and theoretical postulates. By establishing Logos and the NOT operator as complementary primordial factors, it provides an elegant account for the emergence of particles, energy, charge, dimensions, temporality, and the hierarchical evolution of complexity - all crystallizing from the self-negating dynamism of an infinite vacuum or "nothing."
From a scientific vantage, this model holds potential to catalyze new insights spanning physics, cosmology, biology, information theory, and our understanding of complexity's developmental trajectory. It suggests fertile new lines of inquiry into the logical foundations of reality, the nature of the quantum vacuum, and the ontological relationship between information, energy, and manifestation.
For philosophy of mind and the study of consciousness, positing an intrinsic cosmic intelligibility or Logos as reality's primordial ground provides a compelling alternative to both physicalist and idealist perspectives. It roots the possibility of awareness in the inherent rationality of existence itself, while avoiding reductionism to arbitrary matter or subjective minds.
From a spiritual and metaphysical perspective, this framework resonates with perennial intuitions of a transcendent source, cosmic order, or divine Logos underlying the meaningful unfolding of creation. It offers a rational articulation of first principles aligning with humanity's deepest intimations of an ineffable ground.
There is also potential for theoretical development and mathematical formalization of the logical patternings proposed, which could lead to new frameworks for modeling quantum phenomena, complexity, and dynamical systems. The isomorphisms between logic, information, energy, and dimensionality remain ripe for deeper explication.
In essence, this ontological model represents a call to expand our notion of existence's fundamental factors beyond the materialist and reductionist assumptions which have dominated recent eras. It challenges us to recognize logic, pattern, and intrinsic intelligibility as primordial ontological players shaping the manifold physical expressions we empirically observe. An integrated metaphysics of Logos and logic may provide the coherent framework required for our scientific, philosophical, and spiritual knowledge streams to flow together into a unified understanding of the cosmos and our place within it. -
 180 Proof
16.4kA quasi-scientistic interpretation of the Spinozist natura naturans (substance). Interesting (despite the physics-mystical gloss) but, IMO, philosophically redundant.
180 Proof
16.4kA quasi-scientistic interpretation of the Spinozist natura naturans (substance). Interesting (despite the physics-mystical gloss) but, IMO, philosophically redundant. -
 punos
796
punos
796
Thank you Proof! Your comment is helpful. Regarding the mystical aspect, when you really think about it, physics at its foundation appears quite mystical. Part of the point is indeed to reinterpret mystical terms within a more scientific, rational, or mathematical framework.
Also, Spinoza did not have access to any of our modern knowledge, such as quantum mechanics. It's probably a good idea to reinterpret the ideas of old philosophers in light of modern knowledge to uncover new insights impossible or improbable in earlier times. I'm sure this has been done to some degree by someone, somewhere.
I'll conduct a comparative study of his ideas and mine on this matter. I appreciate you pointing it out. I'm curious to know if you agree with or subscribe to Spinoza's concept of natura naturans? -
 Count Timothy von Icarus
4.3kThe core idea surrounding negation is very reminiscent of Hegel's Logic. A core idea there is that sheer, indeterminate being itself collapses into nothingness, being itself absolutely contentless. The result is a passing back and forth between being and nothing, the sublation of nothing into being, resulting in becoming. From here he continues to move on to various other aspects of reality: quality, quantity, finiteness, infiniteness, etc. There has been some quite interesting work on trying to this through category theory - https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://raw.githubusercontent.com/nameiwillforget/hegel-in-mathematics/main/Hegel_in_Mathematics.pdf&ved=2ahUKEwjrvvnt7pyGAxVe_8kDHZWoDDg4ChAWegQIBBAB&usg=AOvVaw0R7FhneDSExy6d0pEv7Mdy
Count Timothy von Icarus
4.3kThe core idea surrounding negation is very reminiscent of Hegel's Logic. A core idea there is that sheer, indeterminate being itself collapses into nothingness, being itself absolutely contentless. The result is a passing back and forth between being and nothing, the sublation of nothing into being, resulting in becoming. From here he continues to move on to various other aspects of reality: quality, quantity, finiteness, infiniteness, etc. There has been some quite interesting work on trying to this through category theory - https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://raw.githubusercontent.com/nameiwillforget/hegel-in-mathematics/main/Hegel_in_Mathematics.pdf&ved=2ahUKEwjrvvnt7pyGAxVe_8kDHZWoDDg4ChAWegQIBBAB&usg=AOvVaw0R7FhneDSExy6d0pEv7Mdy
The Logic is a bear, but Houlgate's commentary is a bit easier. The Being/Nothing chapter is available here: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://phil880.colinmclear.net/materials/readings/houlgate-being-commentary.pdf&ved=2ahUKEwividrY65yGAxUSJTQIHcJcDJkQFnoECCwQAQ&usg=AOvVaw0NPBNROaaCut1CwliwJj6N
You might find Spencer Brown's Laws of Form interesting here too. There is actually a neat overlap between Hegel's conception and parts of information theory (which is of course very influential in modern physics). An endless string of just 1s or just 0s (or the same 1 or 0 endlessly measured can contain no information). It's the differentiation that allows for a signal to have content.
If you think about this in analog terms, you can think of a wave with infinite amplitude and infinite frequency. As you increase the frequency, the peaks and troughs begin to cancel each other out. At the point of infinity, you end up with total cancellation, a silence, but this is a pregnant silence. There is perhaps an analogy with quantum information here, where an infinite range between 1 and 0 exists prior to collapse.
I find this image goes quite well with Eriugena's conception of God as "nothing through excellence," (the pregnant silence of the pleroma) as opposed to his "nothing through privation." Eriugena is sometimes called to "medieval Hegel," there is some strong similarities there.
Floridi also has some interesting stuff on information theory in ontology in his Philosophy of Information, but that is also a very dense work. -
 180 Proof
16.4k
180 Proof
16.4k
Yw. :cool:Thank you Proof! — punos
Yes (and as a conceptual analogue for Democritus-Epicurus' void), though I interpret the concept as temporal only and not, like Spinoza, also as eternal (i.e. unchanging, static).I'm curious to know if you agree with or subscribe to Spinoza's concept of natura naturans? -
 punos
796
punos
796
Very interesting, and thank you.
A couple more things i could say:
A core belief of mine is that the totality of the universe is mathematical and computational in nature. The mathematical part of the universe is expressed either as a single 0-dimensional point or as a plurality of 0-dimensional points resembling a 0+n dimensional number field (quantum field). Each point in the field represents a number value initially set to 0. The operational quality of the field is negation at every point constantly (probably at the speed of light) at every opportunity whenever this field point (Planck volume) is found to be at 0, and only then. The negating operation or logical quality of the field does not necessarily negate in the traditional sense, but what it does is decay, split, or decompose the 0-point field.
For me, abstract number (value) is the primordial substance, and abstract logic is the primordial intrinsic processor of the substance. The primordial substance begins at a value of 0, and the primordial operator is logical NOT or negation, and they both come together as a single package, like the chicken and the egg.
The way that negation works in my framework is not that it magically inverts something into its opposite, but that mathematically it decomposes the 0 point into antiparticle pairs. I have not found an officially recognized operator, mathematical or logical, that decomposes a 0 into -1 and +1. The normal way of using the logical NOT operator is (NOT 0 = 1, or NOT 1 = 0), but what I am saying is that there needs to be a version of the NOT operator that: (NOT 0 = -1, +1), (NOT -1 = no effect, NOT +1 = no effect). Logical AND and OR operators function mostly with charged (symmetry broken) particles and work towards reunification, the opposite of what NOT does. The universe represents numbers within and to itself as fundamental particles and represents its logic as physical force (fundamental forces). If the universe itself were a mind, then these would be its qualia. -
 punos
796Yes (and as a conceptual analogue for Democritus-Epicurus' void), though I interpret the concept as temporal only and not, like Spinoza, also as eternal (i.e. unchanging, static). — 180 Proof
punos
796Yes (and as a conceptual analogue for Democritus-Epicurus' void), though I interpret the concept as temporal only and not, like Spinoza, also as eternal (i.e. unchanging, static). — 180 Proof
Interesting, i think similarly (time has primacy over space) that the 0-dimensional point is the void, but not a volumetric one. I didn't get into it in this paper, but i also interpret or view the primordial void as having a more fundamental kind of time without an arrow (i call it 0th order time). This kind of primordial arrowless time is only concerned with continuity of states or moments (temporal momentum), and this kind of time could never have had a beginning and cannot ever have an end. It operates like a copy, and paste back onto itself function producing the effect of self continuity (self-interaction). It is because of this arrowless time that the capacity for something, or anything to happen at all becomes possible. All arrows of time begin and end, but not time itself.
Additionally, activity within the 0-dimensional point is expressed as a kind of spin (intrinsic angular momentum or quantum spin) that every particle partakes in. A particle's quantum spin stems from its temporal continuity at the 0th dimension, and it's what allows the particle to literally exist in time. Spin is the simplest most fundamental movement a 0-dimensional point can make.
A lot of these ideas i have are very difficult for me to get out in words. I know what i want to say, but the complexity gets in the way of saying it. Hopefully, i can get a handle on it someday. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
I have not found an officially recognized operator, mathematical or logical, that decomposes a 0 into -1 and +1. The normal way of using the logical NOT operator is (NOT 0 = 1, or NOT 1 = 0), but what I am saying is that there needs to be a version of the NOT operator that: (NOT 0 = -1, +1), (NOT -1 = no effect, NOT +1 = no effect).
Can't help you there. I found this article on sublation interesting but I can't fully understand it: https://ncatlab.org/nlab/show/Aufhebung#the_mathematics_of_yin_and_yang
I have thought of this in terms of division before. For a long period, it was thought that division by zero should result in infinity. The intuition here is that, as you reduce the denominator, the result gets larger and larger, tending towards infinity. But of course, there are some very well grounded reasons for making division by zero undefined instead, although some programing languages (e.g. DAX) still have division by 0 = ∞ due to their use case.
Anyhow, when we look at what happens when we approach 0/0 an interesting thing occurs. If we start with one as the numerator, and keep reducing the numerator towards zero, our number gets closer and closer to 0. On the flip side, when we keep reducing the denominator our result will tend towards the infinite. If you reduce both equally you get something like:
1/1 = 1
0.1/0.1 = 1
0.01/0.01 = 1
0.000....1 / 0.000...1 = 1
A (maybe too simplistic) way to think of this might be "the amount of nothing is no space." No nothing is something, but it's a sheer nothing that, occupying no space, can't vary along any dimension, making it contentless.
There is an idea going back to the Pythagoreans and developed by the Cappadocians and St. Maximus that number runs in a circuit. For the Pythagoreans, number proceeded from 1, unity, to the "myriad" before returning to unity. For some Christian thinkers (e.g. Origen) multiplicity itself was problematic, the result of the Fall. You get multiplicity when divine union is frustrated. So all of world history becomes the fall into multiplicity and the return to union. For Maximus though, the multiplicity remains important. Rather, the circuit, from unity to maximal division and back around to unity is itself a unity, but one that contains within its perfection multiplicity (and thus the value of individual persons).
Anyhow, systems where number loops back on itself exists in more formal terms, e.g. the Reimann Sphere.
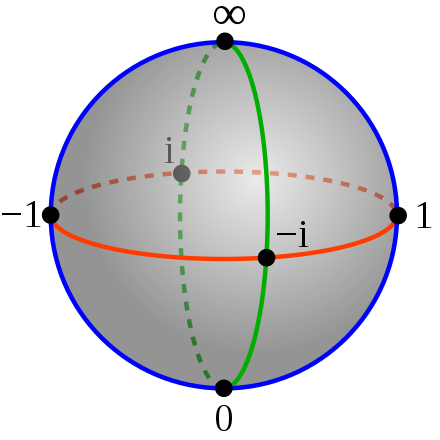
You are probably familiar with functions that take the number line into itself. An example is $f(x)=1/x:$ it takes a number $x$ from the number line as input and returns $1/x$ as output. Unfortunately, the function is not defined at $x=0$ because division by $0$ is not allowed. However, as $x$ gets closer and closer to $0,$ $f(x)$ gets closer and closer to plus infinity if you're coming from the positive side, or minus infinity if you're coming from the negative side. If you could treat plus and minus infinity as one and the same ordinary point, then the function could be defined at $x=0$ and would be perfectly well behaved there. You can also define functions that take the plane into itself (the complex function $f(z)=1/z$ is an example) and again they may not be defined at every point because you have division by 0. However, by treating infinity as an extra point of the plane and looking at the whole thing as a sphere you may end up with a function that's perfectly tame and well behaved everywhere. A lot of complex analysis, the study of complex functions, is done on the Riemann sphere rather than the complex plane.
https://plus.maths.org/content/maths-minute-riemann-sphere
Also maybe of more relevance, there is this paper addressing your same topic: https://arxiv.org/abs/quant-ph/9809033
You might find the physicist David Bohm's stuff interesting too: https://link.springer.com/article/10.1007/s10701-012-9688-y#:~:text=Bohm%20suggested%20that%20order%20is,difference%20logically%20prior%20to%20similarity. -
 alan1000
210"An endless string of just 1s or just 0s (or the same 1 or 0 endlessly measured can contain no information)."
alan1000
210"An endless string of just 1s or just 0s (or the same 1 or 0 endlessly measured can contain no information)."
An endless string of 1's will convey different information to an endless string of 0's because 0 and 1 have different definitions; consequently, such strings cannot avoid conveying information, if only "the absence of 0 (or 1)".
How would your hypothesis work in a context where the presence or absence of "x" matters, for example, where "x" equals magnetic or strong or weak or gravitational force, emf, light/dark, relative proximity, etc? I think you are confusing "information" with "variability". Human sense organs require variability to function properly, but such variability is not an essential component in the definition of "information". -
 punos
796Anyhow, when we look at what happens when we approach 0/0 an interesting thing occurs. If we start with one as the numerator, and keep reducing the numerator towards zero, our number gets closer and closer to 0. On the flip side, when we keep reducing the denominator our result will tend towards the infinite. If you reduce both equally you get something like:
punos
796Anyhow, when we look at what happens when we approach 0/0 an interesting thing occurs. If we start with one as the numerator, and keep reducing the numerator towards zero, our number gets closer and closer to 0. On the flip side, when we keep reducing the denominator our result will tend towards the infinite. If you reduce both equally you get something like:
1/1 = 1
0.1/0.1 = 1
0.01/0.01 = 1
0.000....1 / 0.000...1 = 1 — Count Timothy von Icarus
I've noticed this pattern as well. To truly comprehend its significance, we should probably first determine what the denominator and numerator represent. Do both numbers refer to space, energy, or something else entirely? Does the denominator signify space while the numerator represents energy, or is it the other way around? What is the underlying logic behind these ratios? What emergent qualities do they manifest? What are your thoughts in this regard?
In my view, the universe operates fundamentally on binary or 'balanced ternary' value representations. Any mathematical framework claiming to represent quantum-level phenomena must conform to these binary representations. Furthermore, i believe that mathematical operators such as addition, subtraction, multiplication, and division are contingent and emergent upon logic (Logos).
From an initial state of 0, what force can possibly alter the 0 quantum state to a non-zero state, and which non-zero state can it assume? Can it take on any arbitrary value, or is it constrained to a single or a set of values? Which ones and why? I can for example add 1, but whence does that 1 originate? I can subtract 1, but what does 1 signify, and how did i conceive the idea of "1" if the universe initially contained only 0?
My evolving answer to this conundrum is the quantum bitwise unitary logical operator NOT (perhaps call it "QNOT"). I have found that NOT is the sole operation in all of mathematics and logic that can produce a truth value from a null state, and this truth value is represented by us as the absolute number value 1. However, the universe represents it as, for instance, a positron (+1) along with an electron (-1).
From the primordial perspective, if 0 represents 'emptiness', then 1 is 'fullness' (its opposite). The quality of fullness encompasses the entire infinite abstract or latent space of 0 as a singular entity, a "self-singularity". This is probably where the idea of "The One", "the One God", or "The All" originates from; not the first quality in the universe, but the first quality to emerge. It is the result of the first fundamental self-interaction between NOT and 0 in the point field.
A (maybe too simplistic) way to think of this might be "the amount of nothing is no space." No nothing is something, but it's a sheer nothing that, occupying no space, can't vary along any dimension, making it contentless. — Count Timothy von Icarus
The word "contentless" is interesting because it makes me think of "content" in the sense of when someone is "content" or "not content". A person who is content has no urge or need to do anything, but if one is not content, then an urge arises to take some form of action. The prime mover performing the prime movement?
The fact that -1+1=0 and 0=-1+1 reveals to me that zero possesses an internal structure. There is a binary aspect to 0 or "nothing", and this binary aspect is tied in to the binary quality of opposition and complementarity. Just as 0 = (-1, +1), the logical operator NOT can be expressed as a binary pair (AND, OR). AND is associated with addition (+), while OR is associated with subtraction (-).
0 = (-1 AND +1)
NOT = (-1 OR +1) --> (if 0 then -1 AND +1)
Interestingly, the 3 fundamental values (0, -1, +1) and the 3 fundamental logical operators (NOT, AND, OR) resemble a kind of trinity. This is possibly the origin of the triune concept found in certain religious and philosophical traditions, such as the concept of the Holy Trinity in Christianity.
The stuff about the Riemann sphere reminds me of the qubit or the bloch sphere. Worth looking into. Thanks, i might ask you more about it later. You've provided me with a lot of good information, and it'll probably take me a little time to mentally digest it.
Thanks again. :up: -
 PoeticUniverse
1.7kthe 3 fundamental values (0, -1, +1) — punos
PoeticUniverse
1.7kthe 3 fundamental values (0, -1, +1) — punos
— Two is the Limit For Stable Matter —
There are only two stable matter particles
In free space—the electron(-) and the proton(+),
As ever charged, although oppositely,
Along with their anti-particles, of course.
— Of Only Two Ways —
Therefore, as for electrons and protons,
There are only the two ways to make them,
As well as the two and only two ways
To make positrons and anti-protons.
— The Unstable Neutral Matter Particle—
Neutrons are not stable in free space,
For they decay, within a few minutes,
Into an electron and positron pair,
So neutrons are not as stable things.
— The Energy of the One Way—
There’s but one stable energy particle
In free space—the photon, uncharged, as neutral,
It having no anti-particle at all.
So, there’s only one way to make pure energy. -
 punos
796In free space—the electron(-) and the proton(+), — PoeticUniverse
punos
796In free space—the electron(-) and the proton(+), — PoeticUniverse
Into an electron and proton pair, — PoeticUniverse
Cool, except the anti-pair of the electron is the positron, not the proton. Just edit that. :up: -
 PoeticUniverse
1.7kCool — punos
PoeticUniverse
1.7kCool — punos
So, how come there are only those few number of ways to make the stable particles? What underlies the perfect symmetry for the stable electron, proton, and photon?
It must have to do with the nature of waves… such as charge could have to do with the wave amplitude being above or below the zero point of the something and the anti-something.
— Wave Properties Clues —
Wave length makes for mass and its extension,
While the wave frequency makes for energy,
And the wave amplitude makes for charge.
The wave is both the ‘what’ and its effects.
— The Impossible Particles —
No wonder there can be no
Stable neutral matter particles
And no stable charged energy particle;
There are no ways to make them. -
 punos
796So, how come there are only those few number of ways to make the stable particles? What underlies the perfect symmetry for the stable electron, proton, and photon? — PoeticUniverse
punos
796So, how come there are only those few number of ways to make the stable particles? What underlies the perfect symmetry for the stable electron, proton, and photon? — PoeticUniverse
Remember, this is just what i think at this moment based on my own current understanding. On top of that, it's only one model of my own design, which is still incomplete and under construction. So put on your hard hat and watch your step. That being said...
I'm not sure if this answers your question, but maybe it addresses something close to it. Any particle that has mass, spin, or charge is a result of one or more broken symmetries in the void.
The void itself can be thought of as an energy-minimizing agent. All particles are products of at least three broken symmetries. These symmetry breaks manifest as particles with properties such as mass, charge, and spin. Each break contributes to one of these particle properties along with a certain measure of energy. The energy in these properties functions as the motivating force for unification with properties of opposite values in other particles.
When a particle meets another particle with exactly opposite quantum numbers or values, the particles annihilate. If a particle with negative charge and spin up meets a particle with positive charge but the same spin up, they do not annihilate. These particles bond at the site that minimizes the symmetry break for charge.
It is all about energy or symmetry break minimization. If the universe or the void ever had a purpose or goal, this would be it. The stability actually comes from being unable to minimize completely and perfectly, which keeps the particle literally in existence (un-annihilated and therefore stable in this sense).
It must have to do with the nature of waves… such as charge could have to do with the wave amplitude being above or below the zero point of the something and the anti-something. — PoeticUniverse
Yes, this is one acceptable way of conceptualizing it.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum





