-
What if spirituality is the natural philosophy?That’s a very aggressive stance you have there. I’m not an authority on his mental health, what’s the diagnosis? — AngryBear
Crackpottery is not a diagnosis - well, not necessarily - it is loopy pseudoscience in this case. Whether the guy really is off his rocker or whether he is just peddling this crap in a bid to make some money is really none of my concern. And I wasn't being aggressive - on the contrary, just wanted to give you some well-intentioned advice. When someone sees you citing a crackpot, they might think: "This person is not to be taken seriously. I better not waste my time listening to what he has to say." -
Kuhn, Feyerabend and Popper; Super Showdownconsidering the surge of popularity attributed to both Kuhn and Feyerabend (who where fierce anti-Popperians). I wouldn't say it's a banality. — Pelle
I didn't say all of Popper's ideas about science were banal - some of them were just wrong (kidding!) No, I was referring to ideas like "people trying to falsify eachother's theories" and other pop-Popperianisms that some people, including scientists, swear by. Popper's actual lasting impact on the philosophy of science is far more dubious than his rock-star fame would suggest. -
What if spirituality is the natural philosophy?Laird Scranton — AngryBear
He is a crackpot. You really don't want to bring this kind of crap into a philosophical discussion - it destroys all credibility. -
Nietzche and his influence on HitlerYes I understand Nietzsche is one of the hardest Philosphers to read and understand and congrats to all of you for you impeccable knowledge but some of you do come across as quite brash to someone who is just starting out. I am a mature student who has only recently been granted full use of her eyes over these last two years and I have a thirst for knowledge on the subject of Philosophy. I have chosen Nietzsche because I feel for what I have read so far that he is very misunderstood. — Helen G
Well, one thing Nietzsche is not is clear and consistent, which is why just about every scholar of Nietzsche thinks that he is misunderstood by someone (or even everyone) else. So, you are in a good company. -
Kuhn, Feyerabend and Popper; Super Showdownmodern science does follow Popper's ideas to some extent. The critical discussion around science today is exactly as Popper described: people trying to falsify eachother's theories. — Pelle
This is a banality.
The ideas that are popularly credited to Popper have been around since Bacon. What is right about Popper's prescriptions isn't new or radical at all. -
Is logic undoubtable? What can we know for certain?I would maintain that at least the law of non-contradiction is indubitable in just this sense: it cannot intelligibly be doubted. — PossibleAaran
Yes, even the law of non-contradiction can be intelligibly doubted: see Dialetheism
The a priori status of logic has been under attack for quite some time (as you can see above, even the sacrosanct non-contradiction is not safe). This is true even of the so-called "laws of thought," which is what you must really mean when you talk about logic, because formal or mathematical logic is as diverse and open-ended as mathematics. -
Another question about a syllogismWell, in this set up, we don't know anything about the relationship of odd and even, and we don't know anything about prime factorisations or that even means 'is divisible by 2 with no remainder'... The only premise here which is even related to even numbers and squares of even numbers is (1). — fdrake
Either you understand what is written, or you don't. If you don't, then nothing more can be said. If you do, then you know what "odd" and "even" mean. (But then if you do, you don't really need to go through this logical exercise in order to prove the conclusion - you could prove it by other means.)
I thought it was invalid because it seemed a lot like affirming the consequence to me. If you focus on the 2nd premise, — Ulrik
So the question becomes, can we conclude the statement: 'If the square of a number is even, then that number must be even' from the statement 'if a number is even, then its square must be even'? — fdrake
Why are you focusing on the second premise alone when two premises are given? -
Thought experiments and empiricismI don't know. It seems to me that only a defeasible statement can be meaningfully tested. How do you test a tautology (or a contradiction)?
I am familiar with this thought experiment, but not well-versed in its detailed treatment in the literature. I wonder how much of a point of contention this particular issue is. — Arkady
There seem to be quite a lot of references to the thought experiment in the literature - mostly it is (quite extensive) literature on thought experiments in general, but there are some specific examinations of Galileo's thought experiments, including some critical ones.
I found this paper interesting: D Atkinson, J Peijnenburg, Galileo and prior philosophy (2004)
They argue against the idea that Galileo succeeded in giving, in J. Brown's words, a "destructive" (against Aristotle's law of motion) and a "constructive" (in favor of Galileo's alternative) logical argument. Interestingly, they point to case where Aristotle happens to be right! It is the case of terminal velocity, which, under some conditions and idealizations, is directly proportional to the mass of the falling body. And yet Galileo would have it that this is logically impossible. How could that be?... -
Atheism is far older than ChristianitySomehow I feel I have been deprived of the epiphany I expected, reading the title. — Pair o'Ducks
Yeah, the title is odd: it's supposed to sound provocative, but how is what it ostensibly asserts even controversial?
The author's thesis is stronger than that: he argues that atheism was a "thing" in the ancient world, not just a few individual exemplars. -
Atheism is far older than ChristianityThe "study" is actually a book:
Tim Whitmarsh, Battling the Gods: Atheism in the Ancient World. New York: Alfred A. Knopf, 2015.
Here is the author's presentation: Battling the gods
And a (favorable) review from a classicist: Bryn Mawr Classical Review 2016.06.20 -
Question about a basic syllogismWhat I fail to understand however is that you can conclude 'Some Americans curse' from the premise 'All Americans curse'. You see, I thought if one says 'Some people are nice', one means that 'some people are nice, and some are not', rendering the deduction from 'All people are nice' impossible. — Ulrik
You are not wrong. Indeed, in natural speech, when we say "some A's are B," more often than not we mean that some are and some aren't. If we want to convey the other meaning, we might say something like "at least some A's are B." However, in the context of logic, in semi-formal syllogisms like the above, "some" is conventionally taken to express the latter meaning, that is
In set terminology: A ∩ B ≠ Ø (the intersection between all A's and all B's is not empty)
In predicate terminology: ∃x: Ax ∨ Bx (there exist subjects to which both predicates apply) -
Thought experiments and empiricismHere is a better (IMHO) refutation of Aristotle through thought experiment. Consider a dumbbell:
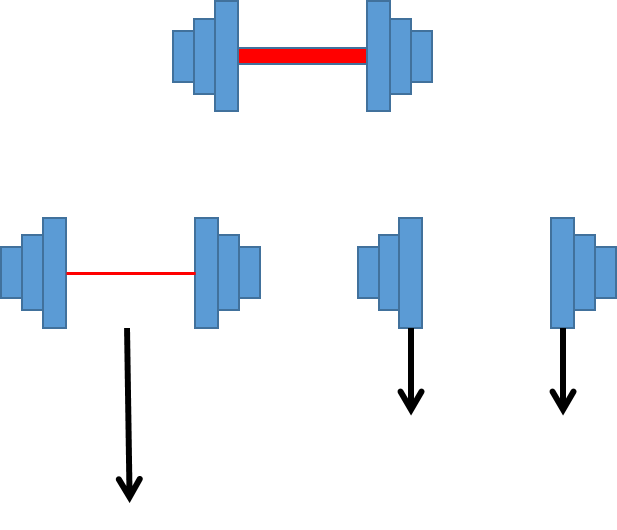
Let's take two such dumbbells. On one of them we will replace the connecting rod with a hair-thin wire, and on the other we will remove the rod altogether. Now let's drop these two "dumbbells" side by side. According to Aristotle, the two unconnected weights should drop with the same speed - so far so good. But the still connected dumbbell, simply by virtue of being individuated as one body with twice as much weight as either of the free weights, should drop much faster - twice as fast, if we take Aristotle's strongest formulation of his law*.
Unlike in Galileo's thought experiment, there is no logical reductio here. But the situation is physically implausible, because as long as the connecting wire is not stressed (and it need not be in this experiment), there is practically no difference between a "dumbbell" connected with a wire and a pair of identical unconnected weights.
* This is somewhat unfair to Aristotle, because in one of his more careful formulations, he says basically that ceteris paribus, the heavier body falls faster than the lighter. Here ceteris is most definitely not paribus. -
Thought experiments and empiricismI largely agree with your treatment of this question, Sophisticat. However, the above assumption (i.e. that the falling bodies behave as if they're separate bodies until the string is taut) seems debatable to me: as the weights were connected by the tether prior to their being dropped, they've always been "one body," and thus it could be argued that the composite body comprising the two weights plus tether would always fall faster than either body alone, given that they've always been one object for the purposes of this experiment. — Arkady
Aristotle, even as Galileo presents him in his dialogue, talks about "natural motion," which apparently is a free fall through some medium, such as air or water (neither Aristotle nor Galileo would contemplate vacuum). But in Galileo's setup, whenever the two bodies interact (the lighter body retards the motion of the heavier body), each body, when considered individually, is being acted upon by the other, and therefore is not in "natural motion." The entire system of two tethered bodies can (in Newtonian hindsight) be seen as one body in free fall, but neither one of the two bodies is in free fall when they interact.
So we can quibble over whether tethered bodies constitute one body, but the important thing is whether they constitute two independently falling bodies. If they don't, as Galileo's thought experiment requires, then Aristotle's law does not apply.
An interesting side note to all of this is that, if Aristotelian physics (or, at least the part of the theory which posits that heavier objects fall faster than light ones) really does imply a contradiction, one must reach the modal conclusion that there are no possible worlds in which heavier objects accelerate faster than light ones under the force of gravity alone! Intuitively speaking (for my intuition, anyway), it seems odd to put such a seemingly contingent physical fact on par with blatant contradictions such as square circles, or objects which are both red all over and green all over, etc. — Arkady
We don't even have to consider alternative physics, because Galileo gets the actual physics wrong. Bodies falling in a medium do not fall with the same speed. Now, Galileo surely realized this (as did Aristotle - he has a number of formulations of his law, some of which account for and even appeal to this fact), so he inserts a proviso that the bodies should be of the same material or the same specific weight. But this doesn't quite salvage his argument: a wood chip will fall slower than a log. And besides, this proviso does no work in the logic of his thought experiment, so it is irrelevant.
Galileo obtains the right result in a vacuum, in uniform gravity - thanks to the fact that gravitational mass is the same as inertial mass. But I don't see how this result can be obtained from a priori considerations. It was considered contingent enough for scientists in the 20th century to conduct sensitive experiments in order to test it. It is a generic consequence of Einstein's General Relativity, but that theory is not a priori either. -
Question about a basic syllogismNo decent people curse
Americans curse
Therefore
Some Americans are not decent — Ulrik
First, it is not entirely clear whether "Americans curse" means "Some Americans curse" or "All Americans curse." (Applying real-world knowledge, it seems more likely that they meant "Some Americans curse" - surely, there are Americans who don't curse?)
Fortunately, the conclusion "Some Americans are not decent" follows either way.
based on the premises it says 'all Americans are not-decent', not just 'Some Americans are not decent'. — Ulrik
But "all Americans are not-decent" implies "Some Americans are not decent," so the conclusion is still true. A valid argument does not have to have the most comprehensive conclusion possible. -
Thought experiments and empiricismIt seems you have missed the point entirely. According to Aristotle: — Inis
Right back at you. As I said right before the paragraph that you quoted, Aristotle (as per Galileo) does not treat of bound systems - his law concerns separate bodies. Galileo wants to stretch Aristotle's premises in a way that is, admittedly, physically intuitive, but strictly speaking, he cannot trap Aristotle in a contradiction by changing his premises. -
Thought experiments and empiricismSo, turning back to the OP for a change :)
If one had to choose a thought experiment to defend Norton's view, would Galileo's thought experiment that two falling bodies fall with the same acceleration be a suitable thought experiment since it can be empirically tested and it also can be written in a premise and conclusion argument form. I am not sure whether this would be a deductive argument though.
Also, wouldn't the assumption that connecting the heavier (H) and lighter ( L ) body makes one body of weight (H + L) mean that one of the premises of the argument would be false. — ADG
This refers to Galileo's famous argument against the then prevailing Aristotle's theory of falling bodies, according to which "bodies of different weight... move in one and the same medium with different speeds which stand to one another in the same ratio as the weights." While the apocryphal story says that Galileo conducted an actual experiment by dropping weights from the tower of Pisa, there is no evidence that he actually did this. All we have is a fictional dialogue between three characters. While one of the characters in the dialogue claims to have conducted an experiment of some sort, Galileo's stand-in declares that "without experiment, I am sure that the effect will happen as I tell you, because it must happen that way."
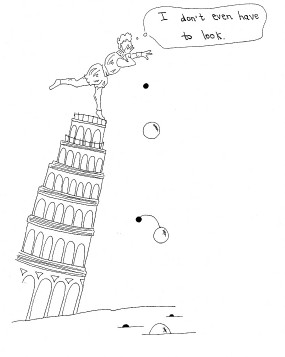
Galileo's argument is brilliant in its simplicity: Take two bodies of different weight connected by a string and drop them together. According to Aristotle, the lighter body will tend to fall slower than the heavier body, retarding its motion. Therefore, the two bodies together will fall slower than the heavier of the two would have fallen alone. But the combined weight of the tied bodies is greater than the weight of either of them, so again, according to Aristotle, the two should be falling faster. A contradiction.
However, as is often the case with thought experiments, this proof can be challenged. Galileo's reductio works by treating the two bound bodies as separate bodies in one part of the proof and as one combined body in another. But is it a legitimate move? Aristotle doesn't say anything about how parts of a bound system should move - he only considers separate bodies. Moreover, while he says that "each falling body acquires a definite speed fixed by nature," it would be implausible to suppose that that definite speed is acquired instantaneously - presumably, some acceleration is taken for granted. So a charitable reading would say that when two separate bodies are dropped side by side, at some later time their speeds will "stand to one another in the same ratio as the weights."

Consider Galileo's setup: two bodies of unequal weight tied by a light string and dropped from a height. If at first the string is loose, the two bodies behave as separate bodies (notice how we are already importing our physical intuitions into the thought experiment!) If that's the case, then according to Aristotle, the heavier body will be falling faster than the lighter one, but that cannot go on forever: at some point the string will go taught. At that point we can treat the two bodies as one (again, a physical intuition). This combined body, if it stays whole (which it won't, but let's disregard that) will, according to Aristotle, eventually acquire a higher speed than either of the two separate bodies had before they combined. But as long as it behaves as one body, we cannot compare its motion to the motion of its parts, since the parts are not separate and independent, nor have they been falling side by side with the combined body: there was a discontinuous transition from two falling bodies to one.
So my conclusion is that Galileo's thought experiment, while suggestive (it seems implausible that the two bodies will lurch forward as soon as they come in contact with each other), doesn't constitute a reductio against Aristotle. -
Thought experiments and empiricismThought experiments are nothing but a form of empirical simulation. For any thought experiment can be substituted for a publicly demonstrable virtual reality simulation. — sime
Thought experiments can be more than that. Some thought experiments explicitly assume counterfactual conditions, unphysical idealizations, etc. The interpretation, the lessons and the value of such gedanken are often controversial. -
Question about a basic syllogismYes, you are right, I interpreted 'are' as 'being equal to', not as class membership. Is thinking in class memberships the right way to approach syllogisms in general? I find it hard to determine what context I can, and cannot use, since, as I understand it now, in logic, we ignore anything that's not in the premises. — Ulrik
You would have to use a formal language to avoid ambiguities (e.g. ⊂ vs. =), but for relatively simple reasoning this isn't necessary. You just need to apply common sense or knowledge of the context to come up with the right interpretation.
But how about this famous argument from Aristotle, where he says:
If A is equal to B, and B is equal to C, then A is equal to C.
In this case we have to interpret 'equal to' as identical to, not as class membership?
If A = B and C = B, then A = C would be correct in that case. — Ulrik
IIRC this is true in Aristotelian logic, where certain types of predicates are simply assumed to be transitive. So this result wouldn't require proof. -
Thought experiments and empiricismSo, the doctrine that "knowledge is derived from the senses" is well and truly a dead doctrine, and I am thoroughly surprised if anyone is wasting their time on it. — Inis
Is this literally the doctrine with which Norton, Brown, et al. are concerned? Have you actually looked at any of the literature? Do you think it reasonable to believe that these and a sizable proportion of other contemporary philosophers would be "wasting their time" on something that is "objectively false" and "well and truly a dead"?
GRW is not quantum mechanics, Bohm has been refuted so many times it's getting boring, Copenhagen is psychology. These are all standard views in foundations of QM.
And, you call me "stupid"? — Inis
I have to say, you leave me little choice. -
Question about a basic syllogismYour mistake is that you interpret "are" as identity (=), whereas from the context it should be clear that "are" here indicates membership of a class (of valuable things).
Such things are easier to understand if you draw a Venn diagram:
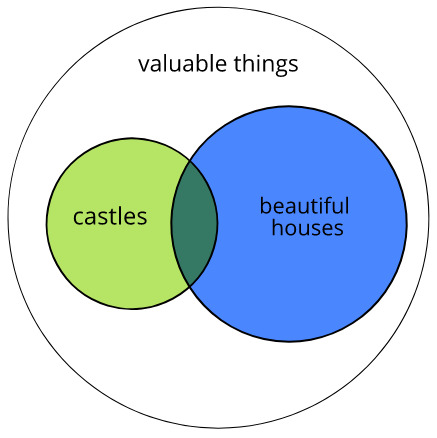
-
Is Determinism self-refuting?If pain has never been causal throughout evolution, then I can see no reason (i) why it should have evolved at all, or (ii) why it should be so unpleasant (if the subjective sensation is not what causes us to withdraw the finger and never has been, the sensation could just as well have been extremely pleasant, since pleasant or unpleasant, it would have made no difference). — Herg
At best, pain signals us about some adverse environmental circumstances or a bodily disorder, so that we attend to this situation and deal with it. But of such situations those in which unconscious reflexes (like yanking a finger out of a fire) are adequate and sufficient are relatively few.
Why is it so damn unpleasant? And why do we feel it, even when there is nothing we can reasonably do about its cause (without the amenities provided by our modern civilization, which evolution could not have anticipated)? Well, evolution is primarily a satisficing process, rather than an optimizing one: it often settles on a good-enough solution. It must be that occasional bouts of misery did not impose as high a cost on reproductive success as the alternatives that were available at the time.
Besides, though I am no more an expert in this area than you are, surely unconscious reactions would have evolved much earlier than anything like pain? Even organisms without any central nervous system have those.
How does that challenge work? — TheMadFool
Well, different people have posed it somewhat differently, and you'll have to read their arguments to understand. Though sometimes simply, even flippantly stated (like Sir Eccles' quote in the OP), it's not so simple really. In my opinion, James Jordan's statement that I quoted in this post is one of the most cogent. -
Evolution is harder with currently evolved organismsWhen I look at current organisms, I see them as very complex and rigid, especially to the extent that their malleability solidifies towards their surrounding environment. At the onset of evolution, simple organisms were more malleable to the variables surrounding them, so changes occur at a fast pace, but as these organisms progressed with due millions of years, their malleability became rigid which is why you don't see evolution occuring today. — Susu
I think you got this idea because you don't have a good feel for the timescales involved (that's OK, most of us don't). Life has been on Earth for about 3.8 billion years - that is, practically since the surface of the planet cooled and stabilized enough for life to be at all possible. But for the first two billion years there were only bacteria-like organisms. Only then did the first organisms of a different kind appeared, from which plants and animals would eventually emerge. From there multicellular organisms took up to a billion years to evolve. Animals in their more-or-less recognizable form (things like molluscs and sea cucumbers) appeared only about half a billion years ago. And evolutionary biologists have been observing evolution in our time for some decades. Decades. Think about it.
Here is a rough timeline in scale:
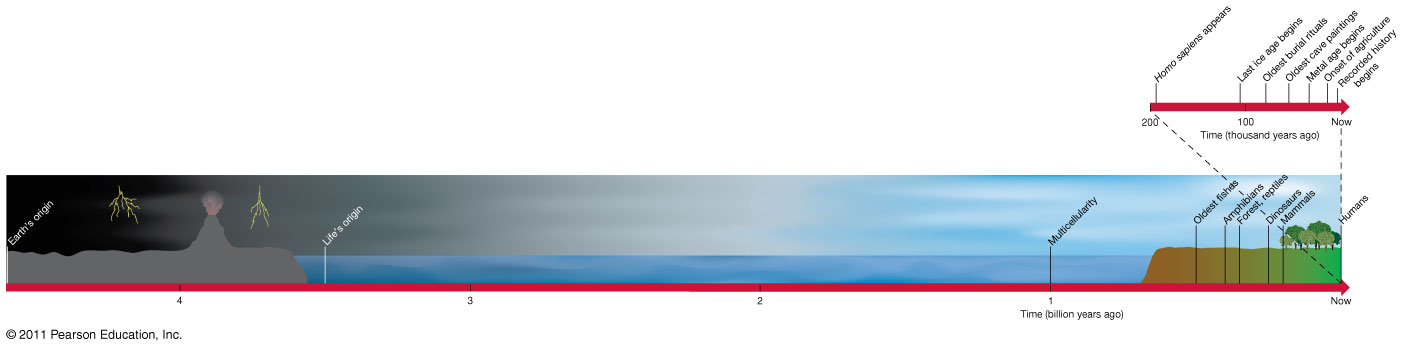
-
Thought experiments and empiricismThis post would benefit from some background reading suggestions for those who do not know what you are talking about.
John Norton, Why thought experiments do not transcend empiricism (2002)
James Brown, Why thought experiments transcend empiricism (2004)
John Norton's other publications on the topic.
SEP Thought Experiments -
Is Determinism self-refuting?My suspicion is that these properties are now epiphenomenal, but were not always so. Consider the pain you feel when you burn your finger. Scientists tell us that you snatch your finger away before you feel the pain, suggesting that the pain is epiphenomenal; but why have we evolved to feel the pain, if it serves no causal function? I think perhaps pain was causal millions of years ago, but then animals evolved a faster response system that by-passes the pain, leaving it as an epiphenomenon. — Herg
So suppose, as you say, that in our evolutionary past pain (qua mental state) served a causal function. Does that mean then that the neurophysiological states that realized this mental state were epiphenomenal? How would that work? -
Pew Survey: How do European countries differ in religious commitment?Here is Levada-Center, a reputable Russian research center:Religion and superstition survey conducted in Russia over a number of years.
Self-identified as Orthodox Christian: 75% in 2017
"I know without a doubt that God exists": 25% (2015) - 31% (2017) (cf. 25% between 2015-2017 in the Pew survey - a good match)
So, three quarters self-identify as Orthodox, but only between one quarter and one third are sure that God exists. Indeed, among "Orthodox" the percentage is only slightly higher: in 2017 34% are sure that God exists, and "one out of every eight... doesn’t believe in God or isn’t sure whether God exists."
There is self-identification (which is what authorities care about) and there is belief - not the same thing. And only a small percentage of self-identified Orthodox are actually observant to any significant extent. But that's not unique to Russia. In the US, for example, people will say that they are "Catholic," but oftentimes they mean nothing more than that they come from a Catholic family (which may not have been particularly religious either). "Jewish" self-identification is even less correlated with religion. -
Is Determinism self-refuting?But isn't that assuming dualism of some kind? Reason has causal import but reason isn't an immaterial thing as of necessity. Right? — TheMadFool
Well, the argument doesn't explicitly assume any metaphysical stance on the nature of reason; it seeks to challenge determinists (in this context: those who maintain that our actions and thought processes are due only to physical causes) on their own ground. -
Is Determinism self-refuting?If logic, reason, etc. are physical things, then they're part of the causal closure in that case, and could indeed have an effect. — Terrapin Station
Right, that would be the identity thesis: the abstract, or the mental just is the physical, or somehow supervene on the physical (and then it's just the matter of "naturalizing" them if you wish to demonstrate the specific connection). -
Is Determinism self-refuting?Let's look at Eccle's argument. If the world is deterministic then what we believe isn't within our control. The argument assumes that rationality is not possible in a deterministic world. But we have computers - perfect rational machines - and they don't have free will. — TheMadFool
You are reprising A.J. Ayer's argument in The Concept of a Person (1963):
The statement that one believes a given proposition on such and such rational grounds, and the statement that one believes it because such and such processes are occurring in one's brain can, both of them, be true. The word 'because' is used in a different sense in either case, but these senses are not destructive of each other... This is illustrated even by the example of a calculating machine. The way the machine operates depends on the way in which it has been constructed, but it is also true that it operates in accordance with certain logical rules. From the fact that its operations are causally explicable it does not follow that they are not logically valid. — A. J. Ayer
Note however that this argument only shows that causal determination does not preclude rationality. The argument that determinism is self-defeating usually makes a weaker claim: that there is no necessary connection between physical causality, which produces what we take to be beliefs and other mental states, and the attributes of truth, logic, reason, etc. that we would like to claim for our beliefs. If the physical world is causally closed, then truth, logic, reason, and other abstract things cannot have an effect on it. And if so, then any correlation between the two realms is either fortuitous or due to some inexplicable preexisting harmony. So the argument goes... -
Is Determinism self-refuting?By his very belief in universal determinism, the determinist, if he is consistent, cannot interpret his opponent's sentence " I possess free will" to be an actual claim to possess an objective property. This is because if universal determinism is true then the only objective meaning the determinist can ascribe in his opponent's sentences are the physical causes that precipitated them. Therefore the determinist must understand his opponent's sentences to be trivially and necessarily correct in an epistemological sense whatever those sentences are, and to be 'wrongable' only in the conventional sense of disagreeing with the linguistic convention adopted by the determinist. — sime
This sounds somewhat like Popper's argument that says that physicalist (let's call it that to avoid confusion) ontology is too impoverished. But a physicalist need not limit herself to just the "objective" language of physical causes. At least I haven't yet seen a persuasive argument to that effect. -
Is Determinism self-refuting?this denial either presupposes free will for the deliberately chosen response in making that denial, which is a contradiction, or else it is merely the automatic response of a nervous system built by genetic coding and molded by conditioning — Eccles
Right. So a determinist cannot interpret his opponent as asserting a contrary epistemological position. — sime
I can't see how you are getting this from the quoted snippet. I think you are just reading into it your own thoughts (which I don't claim to understand). -
Is Determinism self-refuting?You seem to be responding to one word in the title of the thread and nothing else besides.
That's not determinism being self-refuting, i.e. denying or undermining itself through its own entailments - that's just you denying determinism. Not the same thing, and not what the topic is about. -
CO2 science quizWell, the pop-sci story that I've seen is that at the beginning of the Carboniferous period the climate was warm and humid, but during the later part of the period, as carbon was sequestered from the atmosphere, both the CO2 concentration and the temperature declined to approximately present levels.
-
Is Determinism self-refuting?At any rate, that's problematic that Popper is conflating materialism/physicalism and determinism (in my opinion as a physicalist who isn't a determinist). — Terrapin Station
This is not an unusual use of the term determinism - at least it was not at that time. Nowadays determinism is most often taken to mean Laplacean causal or nomological determinism, but in the context of the freedom of will and related topics, determinism was sometimes taken to mean something else. Boyle, Grisez & Tollefsen have a nice discussion of it in Determinism, freedom, and self-referential arguments (1972). They give the following definition:
[N]o special interpretive model beyond the interpretive models used to account for natural events and processes is needed to account for the initiation of human actions; an additional interpretive model used to account for the initiation of actions is a needless proliferation of explanatory machinery. Reformulated in terms of our previous description of the ordinary man's understanding of his actions, determinism implies that there is no warrant for a naively realistic interpretation of the experience of choice among alternatives. Determinism, in the sense in which we are concerned with it here, must exclude any interpretation of that experience which involves a claim that there are really open possibilities among which it is up to the agent alone to choose. — Boyle, Grisez & Tollefsen
So determinism is effectively opposed to libertarianism: "explanations of human actions exhibit the appropriate inferential and nomological pattern of explanations found in physical and biological sciences," as opposed to "explanations of action form a unique type of explanation with special logical and methodological requirements distinct from those of explanations in natural science." (Richard Brandt and Jaegwon Kim, "Wants as Explanations of Actions," 1963).
As should be clear, determinism in this sense is compatible with causal indeterminism.
You are right in that Popper does not make such a clear distinction - in fact, he talks explicitly about Laplacean determinism in places. But I suspect that his thinking was motivated more by the other sense, that of explanatory determinism. Nevertheless, both he and Eccles end up betting on causal indeterminism on their quest to escape explanatory determinism - which I think occasions confusion. -
We are Human thus Imperfect therefore our opinions are imperfectI wouldn't put it past a philosopher to write a book about something so utterly banal and obvious, but why would you want to read it?
-
quantum consciousness, the observer effect, and Westworldwhat people would actually do if science were capable of completely exact predictions of human behavior, and someone were told what they would do next — ernestm
What struck me is that this situation is the same as the quantum observer effect, where particles move unpredictably upon being observed. — ernestm
What people would do if their behavior was accurately predicted is - that's right, they would behave exactly as predicted. Because that's just what you are assuming. The more contentious question is whether the hypothetical situation is at all possible. This question has been debated by philosophers after Dostoyevsky, but it's interesting that Dostoyevsky already wrote about it. I wonder whether he got the idea from someone else or came up with it himself?
As for quantum measurements, they are definitely possible, and some of them are somewhat unpredictable, so that's nothing like that thought experiment. -
A new study proves parachutes are uselessIf not for the "caveat," I would have expected the "no contact at 30 days" group to be 12 out of 12 :)
-
Can hypotheticals prove true in ALL situations and change our pragmatic behaviors?Of course we can't really provide another hypothetical to counter act his hypothetical that would defeat the purpose of his hypothetical and just avoid his hypothetical. — NakedNdAfraid
Why can't we? Because we don't want to make him feel bad about losing an argument?
When making decisions, we do consider various hypotheticals, but if we are being reasonable, we do some selection according to their plausibility and potential impact. We ignore extremely implausible hypotheticals, as well as unimportant hypotheticals. For example, when you are about to sit on a chair, most of the time you do not take seriously the possibility that someone might yank it from under you. Nor do you consider the price of tea in China. On the other hand, a relatively implausible hypothetical with a potentially very high impact may be worth considering, so there is some risk-reward balancing.
Another important thing in a rational decision making is to be consistent about which hypotheticals you include into consideration, and not give them preferential treatment for irrelevant reasons. So if someone asks you: "What if the Gay-Hating God punishes gays in the afterlife?" you are quite in your rights to retort: "What if the Straight-Hating God punishes straights in the afterlife?" Because both are equally valid, albeit extremely remote hypotheticals, at least if you are not a believer in either the Gay-Hating God or the Straight-Hating God. -
Is Determinism self-refuting?
Arguments to the effect that determinism (and/or materialism/naturalism/physicalism) is self-defeating* abound. In The Self and Its Brain Popper cites biologist J. B. S. Haldane's argument (later retracted) from 1932: "...if materialism is true, it seems to me that we cannot know that it is true. If my opinions are the result of the chemical processes going on in my brain, they are determined by the laws of chemistry, not of logic." He traces the argument even further back, all the way to Epicurus: "He who says that all things happen of necessity cannot criticize another who says that not all things happen of necessity. For he has to admit that his saying also happened of necessity." **
* Either in the sense that it is self-contradictory, i.e. it implies its own falsity, or more commonly, in the sense that it undermines rationality, and therefore cannot be rationally justified, even if true.
** Popper acknowledges one (rather week) objection to such arguments, which he addresses, but it is not the objection that Churchland makes, contrary to what he says in his reply to her (Is Determinism Self-Refuting, 1983).
Here is C. S. Lewis, writing in 1947:
Supposing there was no intelligence behind the universe, no creative mind. In that case, nobody designed my brain for the purpose of thinking. It is merely that when the atoms inside my skull happen, for physical or chemical reasons, to arrange themselves in a certain way, this gives me, as a by-product, the sensation I call thought. But, if so, how can I trust my own thinking to be true? It's like upsetting a milk jug and hoping that the way it splashes itself will give you a map of London. But if I can't trust my own thinking, of course I can't trust the arguments leading to Atheism, and therefore have no reason to be an Atheist, or anything else. Unless I believe in God, I cannot believe in thought: so I can never use thought to disbelieve in God. — Lewis
James Jordan in Determinism's Dilemma (1969) identifies and critiques a version of the argument in Kant, as well as in a few more recent writers. Here is his own emendation:
Suppose we are asked to accept the proposition that all our rational assessments have sufficient - not just necessary - causal conditions. In order to show that we ought to believe this, someone would need to produce evidence which is seen to conform to criteria of reasonable trustworthiness and which is recognized to confer, by virtue of some principle of deductive or probable inference, certainty or sufficient probability upon it. But if the proposition is true, this could never happen, for it implies that whether anyone believes it and what he considers trustworthy evidence and acceptable principles of inference are determined altogether by conditions that have no assured congruence with the proposition's own merits or with criteria of sound argumentation whose validity consists of more than that we accept them. Whether we believe the proposition and what considerations we undertake before making a decision depend simply on sufficient and necessary causal conditions that logically need not be, and quite probably are not, relevant to the issues involved in assessing propositions for truth and arguments for validity. If our rational assessments are conditioned solely by factors whose exhaustive statement would omit mention of the recognized accordance of our deliberations with criteria of trustworthy evidence and correct inference, then the recognition of the relevance of these criteria is either inefficacious or absent. Of course, one still might occasionally believe what is true, but this would always be the out come of happy circumstances, never of reasoned investigation. And if this is true of our rational assessment of any argument, it is true of our attempts to determine the strengths and weaknesses of any argument for the proposition in question. If the latter is true, any argument for it is self-defeating, for it entails that no argument can be known to be sound. — Jordan
Alvin Plantinga's Evolutionary Argument Against Naturalism (EAAN) is of the same nature. It takes on the more specific claim that our cognitive faculties arose by way of natural evolution, with no supernatural guidance, but its thrust is basically the same. A similar argument was given earlier by William James. Having been revived by Plantinga, EAAN has spawned its own body of literature.
I have come across dozens more papers discussing the thesis, often in the context of the freedom of will (by those who are impressed by incompatibilist arguments). -
Is Determinism self-refuting?Have you looked into Husserl? — sign
No, I stick with analytics; continentals make my cat-brain hurt :razz: Although the clarity of analytic philosophers can be deceptive (when it is not trivial). For example, I still don't have any clear idea of how "interactionism" is supposed to work: exactly how those worlds and levels are supposed to be affecting each other? Popper doesn't really explain.
SophistiCat

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum