-
Do Physics Equations Disprove the Speed of Light as a Constant?Please return to metaphysics. The real deal is a challenge.
-
The Improbable vs the SupernaturalWould the fully corroborated evidence of supernatural events necessarily lead one to believe in God, or at least in the supernatural;? — Jacob-B
I'll let you know if it happens. :roll: -
The paradox of Gabriel's horn.↪jgill
That's pretty rad! — norm
One of my inventions (probably! You can't tell in mathematics.) :smile: -
Have we really proved the existence of irrational numbers?hat's been the case in my experience too. For applications, though, the dual numbers are actually important today. Some of the autodifferentiation powering machine learning use the forward method, employing dual numbers to great effect (and even hyperdual numbers.) This allows one to compute f(x) and grad(f(x)) at the same time at low cost. — norm
See, I learned something from your post! Thanks, norm.
but felt that she entirely missed the meaning of complex numbers — fishfry
What would you say the meaning is? Just curious. :cool: -
Ever contemplate long term rational suicide?so as a basic dude, the more my body breaks down and my reasons for living become less accessible and then clouded by annoyances like poor sleep, physical limitations and ailments, the balance sheet starts to sway towards I'd rather go out on a high.. — dazed
I've seen this play out in the sport of rock climbing. Sometimes those afflicted follow through. Becoming obsessed with physical performance and not capable of gradually adjusting one's attitude over time is a recipe for termination.
There are times when I think back on my life in the sport, reflect on my performances when young, but I see all that from a different perspective now, and it seems distant and pleasurable but not all that significant. Young, energetic climbers frequently anticipate themselves in old age retaining that fascination that compels them. But it ain't necessarily so. Give yourself a little slack. -
Have we really proved the existence of irrational numbers?I have not looked into SIA — Ryan O'Connor
Weird stuff, IMHO. Low priority in the world of mathematics. -
Religions : education :: states : governance -- a missing subfield of philosophy?. . . that one person should not both write the textbook, and teach from it, and test the students on whether they know their stuff. But, arguing for or against that is going to be a topic of one of those later threads — Pfhorrest
Depends on that person. Is it a good text? Does the prof profit from its sale to his students? Is the prof fair? Not an easy yes or no here. But carry on. -
The paradox of Gabriel's horn.I see that you're a retired math professor so I'm especially keen to hear your feedback, especially if you see a flaw in my argument. — Ryan O'Connor
What makes me uneasy is using a concept like topological equivalence and then discussing slopes and derivatives, which, as you know, do not carry over in that way. As for your continuum ideas, almost twenty years ago Peter Lynds wrote a paper appearing in Foundations of Physics Letters that postulated time having no instants and instead being composed of intervals. Something like Bergson's notions from a century ago. Here it is. -
Religions : education :: states : governance -- a missing subfield of philosophy?A separation of research, teaching, and testing branches of education
is therefore analogous to a separation of legislative, executive, and judicial branches of government — Pfhorrest
Questionable analogy. In academia one person may have responsibilities in all three, in fact usually does. Not so in government. -
Ever contemplate long term rational suicide?Old age is not for everyone. And you never know what's going to go wrong for you or right for you in life. At age 84, my only advice is keep an open mind and stay physically and mentally active as long as possible. I recently returned to my fitness gym, after getting both vaccine shots, and it was a pleasurable experience. But then I have been athletic since the age of 17 and have kept it up. Don't boo hoo when you begin to decline and can't kick the soccer ball like you used to. If you keep at it you may be pleasantly surprised in old age, for your perspective will change. I too have scoliosis and severe arthritis. But four ibuprofen tablets and an acetaminophen taken an hour before exercise can work wonders.
If you make it there, that is. It's a crap shoot. :cool: -
The paradox of Gabriel's horn.You have to remember that these plots are topological so even though it looks linear in the first image I could have just as well drawn it with squiggles. — Ryan O'Connor
I know what you mean here, but reading it makes me uneasy. -
Have we really proved the existence of irrational numbers?LoL. I'm sure the philosophy students in the room were aghast. — Ryan O'Connor
That would be the empty set, Ryan. We were all math majors and the course was taught in the math department. :smile:
You don't know anything about it.
Yet you have persistent critiques of it.
How do you do it? — GrandMinnow
With a certain aplomb. I admire his spirit while avoiding his critiques. :cool: -
Have we really proved the existence of irrational numbers?To me it is concerning that the foundations are so disconnected from the applications — Ryan O'Connor
It's unfortunate the word "foundations" is used in mathematics. Foundational set theory (that intersects with philosophy significantly) and all that revolves around it is a marvelous intellectual area, but a great deal of mathematics flows unimpeded by its pronouncements. Do most seasoned mathematicians worry about the existence of irrational or non-computable numbers? Or non-measurable sets? Not likely.
I've mentioned my own experience before: as beginning grad students sixty years ago we were required to take an introductory course in set theory (foundations). Afterwards the prof - a young energetic fellow - made the statement, "Unless you are really fascinated with the material in this course, I recommend you never take another foundations of mathematics class." I wasn't and I didn't. But I ultimately went into classical complex analysis. Had I gone into a more abstract realm of math I might have needed it.
Could this be an indication that further foundational work is required? — Ryan O'Connor
It depends on which mathematician you ask. Let's hope not. It makes little sense to ask anyone outside the profession.
I'm no expert, but my impression was the math moved toward being totally mechanized, totally formal, totally computer-checkable — norm
And I'm sure Norm would agree, that movement would drive most mathematicians out of the profession. It can't be emphasized enough how much mathematics depends on intuition, imagination, inventiveness, and a spirit of exploration. Devising and proving theorems is an art form. -
The paradox of Gabriel's horn.How can ∞ represent a point? — Metaphysician Undercover
The north pole of the Riemann sphere. But carry on. -
Decolonizing Science?Unfortunately, there are math teachers who criticize a student who solves a problem in a novel way.
-
Decolonizing Science?Before I retired twenty years ago there were discussions in the math department about race and subject matter. We agreed that whenever a topic came up in which a minority had made a significant contribution we would mention that fact. But twisting the subject matter around into some sort of ethnomathematics was not considered.
-
Have we really proved the existence of irrational numbers?Hi ! I'll private-message you about that. — norm
Oh boy they're gonna gossip about the rest of us! — fishfry
Not so, my friend. Norm is mathematically authentic, as are you and fdrake, and I will probably learn something from his posts, as I have from the two of you.
I'm of two minds about revealing anything about the expertise of math people on this forum. I realize the knowledge may intimidate some others and dissuade them from contributing their ideas. Or it might have the opposite effect of encouraging attacks on academia. Oh well, not a big deal. -
Have we really proved the existence of irrational numbers?After years of formal study (proof writing), I still would argue that intuition is primary and that math is a language — norm
What's your background, Norm? Another math proof on the forum? If so, welcome. :smile: -
Complexity in MathematicsConnected with the ideas of "complex" and "complicated" in proofs is the word "elementary", which, when used by a mathematician, usually does not signify "simple" or "easy", but refers to the level of a mathematical argument, specifically that that argument involves only basic concepts in the specific subject area. Some elementary proofs are very complicated. Others, not so much.
"Non-elementary" usually means the argument involves more advanced concepts and results, and may actually be fairly straightforward and uncomplicated - or not. :cool: -
Have we really proved the existence of irrational numbers?In your professional research, did you have the feeling that you were investigating aspects of truths outside yourself that you were trying to find out about? — fishfry
I'm more or less continuously involved in light, unimportant research these days. As an example, I've defined a variation of linear fractional transformations in which the normally constant fixed points are themselves functions of the underlying variable. Then I search for criteria that produce convergence upon iteration. I definitely look for "truths" outside myself, and it's this exploration that's fascinating. Knowing that such truths depend ultimately on axiomatic structures has no bearing on my minor investigations, and the very thought of moving around symbols in a formal game is anathema.
I was once a rock climber and it was the delight of exploration that was intensely compelling. :cool: -
Have we really proved the existence of irrational numbers?One can take the viewpoint that symbolic math is a human endeavor; and that a thing has mathematical existence whenever a preponderance of mathematicians agree that it does. — fishfry
It's true, math is a social activity, but I bet a lot of it exists without a preponderance of mathematicians even being aware of it, much less agreeing it exists. A single practitioner can have an original idea, one that assumes mathematical existence at that moment.
Wiki: "Existence is the ability of an entity to interact with physical or mental reality."
On the other hand, it does take that kind of recognition to establish the importance of a mathematical idea in the mathematical community.
Once again, a topic of limited interest to practitioners. :smile: -
Problem of Induction HelpI'm lost on why the problem is such a big deal — Darkneos
It's not. Seems like common sense. -
Complexity in MathematicsIs this thread intended to find something akin to the p vs np problem (related to complexity in computing)? — emancipate
Good question. I think there is confusion regarding complex in a technical sense and complicated in a more general sense. I know of no "scale" describing levels of complication in a mathematical proof, although when one conjectures a proof path it may be apparent that low or high levels of complication might ensue. And maybe there are practitioners who speculate "Why this looks to be about an eight on the scale of complexity!"
Again, a discussion of mathematics that mathematicians pay little attention to. But fun for amateur philosophers. :smile: -
Complexity in MathematicsI have no use for category theory, but it does attempt to generalize areas of math that have similarities. I fear your knowledge of mathematics is so minimal that we are not getting anywhere here. Since I have been a mathematician (over fifty years) the subject has grown so dramatically and is so complex now I understand little of it myself.
-
Complexity in MathematicsA lot of people are baffled by this topic for some reason, where I see this in a sense very apparent in mathematics nowadays to talk about the sort of lack of categorization, that can even at all begin or take place! — Shawn
Category Theory -
The paradox of Gabriel's horn.(and perhaps you would even agree that the greatest value which y never reaches is 0) — Ryan O'Connor
There is no such value. Might it be 100? Or 1000?. y=1/x, x>1 has a greatest lower bound, 0, which it never reaches. Your attempts at the philosophy of mathematics may never bear fruit if you consider this a cogent statement. -
Best forums for the philosophy of mathematics?Of course, Stack Exchange in mathematics is sort of a forum, and the participants include very knowledgeable professionals, although not so many mathematical philosophers. Very few on TPF have any graduate math experience. Exceptions include fishfry and fdrake, both of whom are up to speed on modern math topics including foundations, which overlaps philosophy. I retired over twenty years ago and am not as reliable. :sad:
-
Complexity in MathematicsSure, but this is quite a conundrum towards the notion that everything in mathematics should or is determinate. — Shawn
The question of whether mathematics is created or discovered has been around for a very long time. This, perhaps, is not precisely what you are asking, but close. An act of imagination may lead to interesting results that are determinate, but the original thought might never arise. Then all that follows will not exist. An original thought is required to set the train in motion. Is that thought determinate?
Let's suppose a math guy has that original thought, and a process unfolds in a determinate manner, then someone else has an original idea that influences the direction of that process. The second guy is part of the process, but his thought may not be determinate.
Most mathematicians pay little to no attention to issues like this. I never did. :cool: -
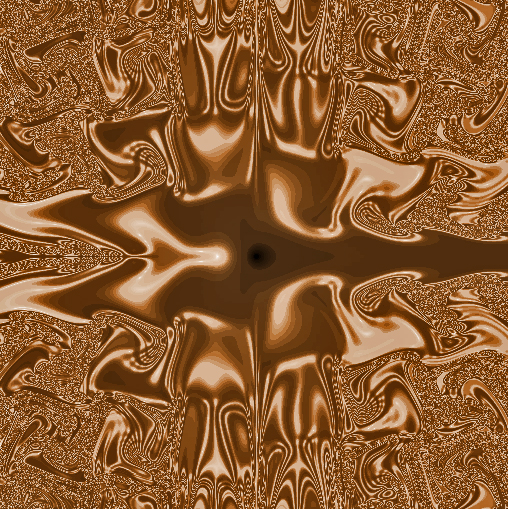
What is the relationship, if any, between emergent properties and quantum mechanics?Is this the result of one of your mathematical formulas ? — Pop
Yes. I've developed the elementary theory of infinite compositions of complex functions in the complex plane - a subject of very, very low importance in mathematics. It's a kind of dynamic systems. The image arises from a BASIC program I wrote some time ago.
David Chalmers, a philosopher and social scientist, wrote a nice article on weak and strong emergence a few years ago. -
"Closed time-like curves"Scientists don't need to think about philosophy all the time but they do this often while doing theoretical physics — Gregory
No argument from me. -
"Closed time-like curves"Penrose's conformal cyclic cosmology says, according to his interviews, that the universe will expand until "it no longer knows what size it is". You have to think philosophically to unpack what that means — Gregory
And that is precisely what the Nobel Prize mathematician/physicist, Penrose, tosses at us. His is philosophical speculation by a revered scientist - not a non-scientist philosopher. That was my point. To philosophize in modern science one needs a science background.
The point being that philosophers can help scientists with conceptual orientation? — Banno
Yes, those poor scientists need a course in critical thinking skills taught by a philosopher. :roll: -
"Closed time-like curves"Their ideas bring paradigm shifts which allow scientist to frame theoretical matters in new ways. Philosophers don't do the measurements but measurements can never stand alone without conceptualization of them and those concepts have much to do with what is discussed in philosophy — Gregory
You may have a point, but I am unconvinced. You would have to demonstrate this philosophical prowess in examples in the modern world, not olden times. -
Eclipsing brightness.Namely, the decreasing amount of philosophers or scientists that exert too much of an effect on a field by making their name known.
Gödel did this to mathematics. — Shawn
He brought to light a fallibility in the subject, but it's not a concern in much of mathematics. However, in the future it may turn out to be very important. Who knows? -
What is the relationship, if any, between emergent properties and quantum mechanics?Weak emergence, weak relationships > The emergent properties apparently aren't very strongly connected to the parts — Kaiser Basileus
"Weak emergence" is a technical term and does not mean "weakly" emergent. It implies the equivalent of a computer program producing an unexpected and largely unpredictable outcome. Thus the image I posted. -
"Closed time-like curves". . . but science can't do without philosophy whether you like it or dislike it — Gregory
Progress in science requires lots of speculation by scientists, and some of this could be called philosophy. But to stipulate that philosophers untrained in science can trigger scientific revolutions is a stretch. :roll: -
What is the relationship, if any, between emergent properties and quantum mechanics?Emergence is identical to relationship — Kaiser Basileus
Here is one of my examples of weak emergence. What is the "relationship"?
-
Complexity in MathematicsHuman thought and ingenuity is paramount in creative mathematics. There is no way to determine this in advance. Lots of "aha!" moments. :cool:
jgill

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2025 The Philosophy Forum