What I’m tempted to believe, is that those ‘formal constraints’ can be conceived as being latent possibilities that become actualised by evolutionary processes. — Wayfarer

Yep. That is structuralism. It is why maths of that ilk - the maths of symmetry - has proved so unreasonably effective in physical theory.

So plenty of different traditions of thought get it.

there is a world of difference between hylomorphic dualism.., — Wayfarer

Yep. But then also, hylomorphism is essentially triadic. The actuality of substantial being arises out of formal constraint on material uncertainty.

So what Pattee argues is this triadic story. Life and mind have substantial being as a result of the biological interaction between information and dynamics.

Killer argument for dualism, in my view. — Wayfarer

Whatever affects the physical is, at least in part, also physical. DNA, for instance, is physical, no? — 180 Proof

Hah. I just spent the morning on this point.

DNA is necessarily physical, but also as little involved in the physics of the world as possible. Every cell has 2m of genetic sequence - several billion nucleotide pairs - packed into space about 6 microns across. A compression ratio of 333,333 to 1.

So from the dynamical perspective of physics - real-time interactions in 4D - DNA barely registers as a dot of material. It has basically no dimensions to speak of. It is physical - but in a way that negates what we normally mean by physical.

However is that a killer argument for a dualism that is any way unphysical ... in the manner this is normally understood by idealists and others?

Well the whole point of Pattee is about the epistemic cut, the modelling relation. Genetic information is meaningful only insofar it regulates entropy dissipation. It is information doing work by running down environmental gradients. It is thus a response to the constraints of the laws of thermodynamics. It is local creativity harnessed to the same old general cosmic project of achieving the equilibrium of a heat death.

the real world has both good & bad properties, from the human perspective, — Gnomon

Math includes both positive and negative values. — Gnomon

This doesn't stack up for me. And organic and immanent metaphysics instead emphasises the complementary nature of symmetry breakings and the reality of chance.

So if there is "good and bad" in the world, this is only a well-formed dichotomy if both sides are part of the one deal.

And if there is "positive and negative" in the world, this is just a simple mirror-level symmetry - easily reversed as it is a symmetry breaking on a single scale of being and so not the complete asymmetry of a dichotomy, a symmetry-breaking that itself produces hierarchical scale.

So symmetry-breakings that work - at the cultural level you seem concerned with - would be ones like competition~cooperation. A functional society is one that balances local or individual differentiation against global or general integration. There has to be the creative energy of selfish striving, and there has to also be a general social project that is the context and meaning for that individual freedom.

To talk of "good and bad" is way too simplistic - a dualism that wants to be reduced to a monism.

If you can't see the need for both sides of the equation - as you can with the matched and yet asymmetric social qualities of competition and cooperation, differentiation and integration - then you aren't thinking in sufficiently fundamental terms.

In maths, positive and negative add up to nothing. If you go left, you can go right, and end up back where you started. Unless your symmetry-breaking produces scale, every difference becomes just a self-annihilating fluctuation.

This is why the Big Bang needs some hidden asymmetry in its particle production. It has to make a difference to be a left-handed or right-handed particle, otherwise particles are produced and just as fast annihilated.

So we know from good argument that reality can only arise via proper dichotomies - ones that result in scale asymmetry. Each side of a pair is defined by it being as far away or unlike its "other" as possible. And yet also, that makes both equally necessary as each is the ground to its other.

Your argument falls apart before it gets started if it is couched in merely anti-symmetric terms like positive-negative and good-bad.

Since Reason, Character, and Emotion are characteristics of our world, specifically the Cultural aspects instead of the Natural properties, the First Cause must have possessed the Aristotelian Potential for those same qualities. — Gnomon

Biology is characterised primarily by the functional dichotomy of competition~cooperation. It is "reasonable" - in the Peircean sense - that life has hierarchical organisation. It is divided by the asymmetry of being locally spontaneous or indvidualistic, and globally cohesive or interdependent.

Even bacteria form biofilms. The planet's climate is regulated by a balance of photosynthesis and respiration that maintains a liveable atmosphere. So from top to bottom, over all scales, life is based on the "goodness" and "reasonableness" of being balanced by its two opposing tendencies.

Aristotle got it to the degree he stressed hierarchical order and the unity of opposites.

But you are taking things back to a simplistic religious framing that just accepts there is a problem of evil, or a problem if a creator isn't the determiner of every detail.

These are just problems if your metaphysics is stuck at the level of symmetry-breaking or dialectics which only thinks in terms of a single scale of being - a world where every left is matched by its right.

A more complete symmetry-breaking produces asymmetric scale or hierarchical order. You arrive at a local~global story where two opposites anchor the two extremes of scale. It then becomes clear that both extremes are necessary for there to be anything at all. As conflicting impulses, both are equally necessary.

Once you have developed your metaphysics to that point, all the causality is within the model. You have arrived at an argument with self-organising immanence.

As a result of programming a Singularity with design parameters (laws & initial conditions), a prolonged process of Evolution began, and will have an end. The End will be the output of the program. And, due to the inherent randomizing uncertainties, presumably even the Programmer does not know exactly what the Final Answer will be — Gnomon

But talking of a programmer immediately makes chance a big metaphysyical problem. Computers are deterministic devices. Chance doesn't even enter the story. And to claim some "swerve" to introduce uncertainty is a patent act of desperation.

So it is much better to argue like Peirce and other organicists. Chance and necessity become the complementary extremes of Being - the two poles that unite to arrive at the balance that is actuality.

And this is what physics argues about the Big Bang. Chance is real in nature as quantum indeterminism. Necessity is also real as the constraints of a decohering thermal structure. At the Planckscale, these two contrarieties have exactly the same scale. The universe is as curved as it is hot. The container is indistinguishable from its contents. But an instant later, the two are already being divided in their opposing directions by the dichotomy of cooling~spreading. The curvature flattens enough that there is some measurable degree of spacetime. The heat spreads enough that there is some measurable degree of localised energy density.

So your story predicts neither what physics has figured out about the start of the Universe, nor what sociology has figured out about the organisation of biological collectives.

So, my story can only be judged by its philosophical explanatory power, not by its empirical evidence. — Gnomon

Good metaphysics grounds good science. But even most scientists don't understand why they wind up where they do. That is why quantum indeterminism, or human altruism, become the scientific version of the old religious puzzles like the problem of evil, or the problem of God's omnipotence.

Everyone's metaphysics must divide the world somehow. Symmetries must be broken to get any kind of reasoning started.

But what we see is that most folk get stuck at the first step - a symmetry breaking that only speaks of two directions at the one scale of being. Go left, or go right. Add more, or subtract to get less. Say yes, or say no.

Productive metaphysics instead continues on from this kind of "dualism yearning to be monism" to a fully-broken dichotomy - one with the asymmetry of a hierarchical or triadically-developed scale. The division has to be complementary - mutually exclusive/jointly exhaustive - so that all its causes are to be found within it. No need for transcendence.

So, Transcendence wins by a mile. Yet, it is still Structuralism. :nerd: — Gnomon

Why would the Big Daddy in the Sky go to all the trouble of pre-arranging an anthropically structured Big Bang that takes 13 billion years to eventually deliver the fleeting blip of a biofilm on some random chunk of real estate?

Creating it in a week, complete as a Garden of Eden, makes more sense if you want to talk probabilities.

And the Las Vegas odds, of such a cosmic-coincidence-of-initial-conditions occurring in finite time (in eternity anything possible must happen), are a bad bet. — Gnomon

Remember that the claim of the Standard Model is about there being a very limited variety of mathematical symmetries for nature to pick from. And indeed, ultimately, just the one final one that is the simplest.

If you want to make an argument here, you need to argue against the odds of wheels being circular. And I note, you carefully avoided trying to argue against that.

Many things we once considered brute facts have turned out to be explained by even more fundemental forces and particles. The onion keeps being peeled back. A lack of ability to progress in explanation does not mean there is no deeper explanation. — Count Timothy von Icarus

But if you study particle physics, you will find this isn't how it works.

We happen to now live in an era where the Cosmos is ruled by its mathematically simplest possible symmetry - the U(1) of electromagnetism.

And when we wind back to recover earlier higher symmetry states, like the SU(3) of the Big Bang's quark-gluon plasma, we see how everything we love and hold dear - all that "matter" and all that "void" - dissolves into a hot confusion of nothing very definite at all.

Keep winding the clock back to the Planckscale and all useful particle structure or spacetime geometry goes out the window. The maths of symmetry itself dissolves. There is a lack of constraint of any kind once you get out beyond 24-dimensional SU(5), or 248-dimensional E8, symmetry stories.

So modern physics rests on concrete knowledge of Lie algebra. The brute facts here are Platonic. :smile:

The onion is tightly structured when its dimensionality is as strongly limited as it is possible to imagine - when all dimensional possibility has been crunched down to just a 3D realm in which the U(1) of EM is present as the concrete limit. But then wind back from that final destination by adding back dimensionality and all that tight structure begins quickly to come undone.

Like leaving town for the country on a dark night, you soon pass by the bright-lit city limits with all its neat regularity of 24 and even edge-of-town 248 dimensional maths. Occasional flashes of sporadic simple groups light up the darkness like truckstops, but even those become increasingly rare.

Travel forever and you may even reach the Monster group.

But the point is that the onion fast runs out of layers to be peeled as its dimensionality expands so fast that it becomes an entirely different kind of thing - a beetroot perhaps. :grin:

And likewise, talk about the Big Bang has to give up on overly concrete notions like spacetime and matter. A 4D vacuum filled with a quantum foam is about where things begin to start.

Beyond that, and there ain't even enough dimensionality to constrain anything in a useful fashion. Everything is too curved or disconnected to be part of any larger coherent sense of structure.

So every philosophical debate about the creation of the Cosmos starts by taking stuff for granted that science and maths already tells us we shouldn't be taking for granted. Beyond the Big Bang, concrete dimensionality and materiality have already left the room.

But he seems to be in favor of “transcendental framing” of the FreeWill question, — Gnomon

He means that life and mind transcend their worlds by being organisms with an intentional point of view. They are in a semiotic modelling relation which puts them "outside" the material world they have a need to control.

So no. He doesn't argue for a spooky dualist transcendence. He is just talking about how organisms transcend their environments by being in a modelling relation with them.

An organism has choices due to genes and neurons. Humans have even more choices due to linguistic and numeric habits of thought.

So, you agree that the ultimate source of “habitual” [regular, reliable] behaviors, rather than acquired in the process of evolution, could inferred as laws of nature [necessities] that predate the Bang. By that I mean, if-then instructions for system operation that were programmed into the seed (Singularity) of the Big Bang? — Gnomon

I wouldn’t use that computer jargon. My argument is structural. Probabalistic systems go towards their equilibrium states.

That “duh, everybody knows about heat death” conclusion came as a surprise to Einstein, who assumed a stable and eternal universe in his calculations. And only when faced with contrary evidence, was forced to rename his Cosmological Constant as what we now know as Dark Energy. — Gnomon

Interesting version of the history.

To me, that “explanation” is what he is arguing against -- saying “they come to look less like explanations than descriptions". In other words, describing the effect is not the same as explaining the cause. — Gnomon

I don't believe you followed what he says. But then, I don't think Tallis is that hot a writer either.

Those who prefer to call those dependable regularities “habits” are implying that they could have been otherwise. — Gnomon

Nope. The structuralist view is just arguing that the regularities of nature are immanent rather than transcendent. They emerge from the chaos of possibility as structural inevitabilities, rather than being God-given laws that animate matter.

But how would they know that, except by re-running the program of evolution several times to see if each execution followed the same basic path. — Gnomon

It's like when Og invented the wheel. Re-run history as often as you like. Let the whole tribe test every geometric possibility. The story always comes out the same in the end. Wheels wind up being circular. Folk wind up getting into the habit of thinking of circles when they want stuff to roll, regardless of whether they have "freewill" or not.

All we know for sure is that Nature seems to be constrained by built-in limitations. So, if you imagine a reality with different constraints you will be dealing with imaginary “woo”, rather than with Reality as we know it. — Gnomon

I'm not arguing that different realities are possible. As a structuralist, I am instead saying our own Big Bang universe is very likely to be the only one of its kind as a consequence of the "strong structuralism" principle.

Maybe you might want to argue for worlds based on other symmetry breakings than the SU(3)xSU(2)xU(1) of the Standard Model. But maybe also, these just are the only series of phase transitions by which a material existence could emerge - one that, Og-like, had to fiddle around with triangular wheels, and square wheels, before arriving at the greatest simplicity of a round wheel.

Can you suggest a simpler baseline gauge symmetry than the U(1) of electromagnetism? The symmetry of a single rotation/translation, or sine wave?

Once you arrive at the universal simplicity of a circle, beyond that you can only aim at the greater simplicity of a circle that is even more circular. Or in other words, there is no beyond. You have arrived at the limit of that kind of "endless" possibility.

The contest here is between two ways of looking at the metaphysics of Being - the transcendent and the immanent. And it is not even a contest.

Having noted that [natural] "laws somehow act upon the 'stuff' of nature from outside it", and that [natural] "laws are a 'quasi-agency'", he seems to be poking his nose into fundamental mysteries. — Gnomon

He was pointing out how this way of speaking retains a transcendental framing that doesn’t make causal sense.

The error of thought is in thinking that the material world is essentially passive stuff that needs to be made to move. That then raises the question of how particles get moved by “laws”.

But if you switch to a constraints-based perspective - a Peircean metaphysics of habits - then the presumption is that nature starts “in motion” and becomes organised by globally emergent patterns. Temperature falls and “laws”, or the constraints of symmetry breaking, get locked in.

Speaking of "outside nature", how could the Big Bang -- the first stage of an ongoing series -- be labelled a "habit"? Are you implying that it was just another routine step in an eternal cycle of repetitions? — Gnomon

The start would be the least habitual possible state of being. It would thus be the most chaotic, the most vague, and the most symmetric state of being.

This we can know just by rewinding the way things are. The Planckscale gives us this answer. At the Planck temperature and energy density, fluctuations are the same size as the world that is meant to contain them. And talking of a time “before” such a state is like asking about a state more circular than a circle. Time only begins once energy fluctuations become smaller than the spacetime that contains them. It is only with cooling-expanding does the possibility of change, difference and history become a reality worth mentioning.

If the universe is prevented, by Entropy, from "ever returning" to it's initial state, that means it's a one-way trip. — Gnomon

You mean, the future is the Heat Death? Well, duh.

But, since the BB was indeed a "big deal" for those of us who ask "why" questions, trying to de-mystify the provenance of the BB is an act of Wisdom, not necessarily a slippery-slope to Woo. — Gnomon

But you can only argue this way by rejecting the alternative that Tallis writes about. As I say, if you presume matter is passive and at rest, then a transcendent hand is needed to get it moving. But if instead you presume matter starts free and restless - just a fluctuation - then organisation will emerge simply because fluctuations will all start to interact and collectively fall into constrained patterns. A history of accidents will accumulate in the same way randomly falling raindrops will start to carve the habit of a river in a landscape.

Have you simply misunderstood Tallis here? You are taking the view he critiques.

But, by reflexively labeling all such "before the beginning" questions as Woo or Weirdness, would tar many serious scientists and philosophers with the same brush as the "religious nuts" and "wacko weirdos". — Gnomon

You are quite right that many physicists just talk about the laws of nature as if they were written in the mind of God. Many are indeed believers in creators. Many believe in a time before the Big Bang. Many believe in all sorts of things consistent with transcendental causality.

I agree they are dealing in woo to the extent they remain mired in such an ontology.

By imposing its will, human nature gains the freedom from natural laws, that allow it to become a guiding agency astride the horse. Thus a Metaphysical Principle rules over the Physical Habits of Nature. Which raises the "dubious" question of who or what was the Lawmaker, Regulator, Selector, Agent, Rider for the powerful Big Bang horse. Is that too woo to be true? :smile: — Gnomon

Aren’t you just re-mystifying the view that Tallis wants to de-mystify?

The Big Bang falls within his description of Natural Habits. Regularity is emergent as symmetries are broken and the general cooling-expansion of the Universe prevents its ever returning to its less organised past.

The quark-gluon soup was a moment of featureless hot generality. It was followed by symmetry breakings that created a world organised by the strong, weak and EM force, that has Newtonian masses moving at slower than c, and so on. The laws of particle physics, then eventually elemental chemistry and code-regulated biology, eventually emerged.

The Universe kept cooling-expanding and further ever-more specified levels of “law” emerged like a rocky shoreline with the tide going out.

So everything is unified as a tale of dissipative structure, Chance becomes increasingly constrained in its forms.

But at the same time, chance is becoming increasingly specific in its form.

The quark-gluon soup becomes a collection of broken-out different forces and particles. You get the possibility of protons and electrons, thus atoms, and thus chemistry as a higher level of dissipative structure.

So from the generality of vanilla chaos, we get the specific randomness of chemistry on the surface of the earth. We have dissipative structures like geothermal ocean floor vents that are where life can gets its own metabolic start.

Thus a planet like Earth is already both severely constrained by an accumulation of cosmic constraints, and yet also left with matchingly definite local degrees of freedom. It is already a highly complex system just with its plate tectonics and atmospheric weather systems.

And then life and mind arise as another level of code-based causality - one both constrained and enabled by that accumulation of physics, chemistry and planetary geology. We have to obey the second law of thermodynamics, but we can also accumulate free energy to spend how we like.

Science simply becomes a way of looking at that situation through the eyes of a culture that wants to understand its reality in terms of the causal levers it can pull, the buttons it can push, to control the material possibilities we find in the world.

So where is the woo? The Universe is organised by thermodynamics. That results in pockets of complexity like a planet. Code-based dissipative structure like life arises within entropy gradients like a thermal vent, and then a photosynthetic flux. Eventually that life becomes organised by higher levels of code such as neurons, words and numbers. It develops a “selfish” point of view that imagines itself as the technological lord of creation.

Big deal. :razz:

I didn’t say it was discovered there.

But looking forward to your book! Good luck.

But the ideas, the imagination is what truly counts. Math hides this. — Prishon

Surely maths is what converts the intuitions into actual counting? It reveals the degree to which an idea works …. in terms of numbers to be read off instruments and dials.

I see irony here. Kant says we can’t access the noumenal. The pragmatist nods a head and says, yes, that is why we have to turn our descriptions of reality into a mathematical theory that takes as its evidence … tallies of marks that some meaning can be read into.

The constraints of phenomenology can’t be broken. But they can be better organised by a shift from everyday language to a rational structure that accepts, in the end, we are only assigning interpretations to numbers on a dial we claim to have accurately read.

I enjoy the confounding fact that science arrives at its realism by way of stringent Copenhagenism. In the end - to speak of the thing in itself - we just have to convince each other in our little circles of rational enquiry that we shared the exact same idea (some equation), and we observed the exact same numerals appear on a dial just as we were led to expect.

Talk about humble bragging!

No one can give a satisfactory account of mass creation (in the sense of saying what actually the math describes; — Prishon

But folk are always trying to provide those kinds of intuitive stories. Like a famous celebrity, a particle would cross a crowded room at light speed if it could. But it’s celebrity causes it to become entangled by the cloud of interactions with these well-wishers. It has a mass and so it’s progress is proportionately slowed.

Goldstone bosons eaten up by the gauge field fir the weak interaction? Nono. I donot buy that. They could be wrong you know. — Prishon

But how else to explain why the weak force is massive and yet the EM photon flies free … at a massless speed of light?

It could be wrong, as indeed any conception of the noumenal could be wrong. But again, that is another advantage of numbers over words. With the logical structure of mathematical claims, the restriction of all claimed evidence to numbers publicly displayed on the dials of instruments, the mathematically-expressed proposition can just be flatly wrong. Everyone present can point at the dial and laugh at the great embarrassment of the failure of a prediction.

But let folk mess around with words and they can come up with any number of confusions that claim to be “theories”, yet fall short of the dignity of even being able to be wrong.

Words are of course very good at telling truths, or falsehoods, at an everyday social level. As theory and evidence, that is the language game they were designed for.

But science is mathematically-definite claims married to numerically-precise acts of measurement. Agreeing that the appearance of a number on a dial proves a theory and ain’t just a lucky fluke requires another level of statistical super-structure. However that supports the general contention here.

So if you think the Higgs mechanism could be wrong - that there was something shonky about the dial reading at CERN - your doubt doesn’t mean much until it is elevated to a level that is itself framed with a technical precision.

You think I have collegues? I only studied there. Particle physicist is not my daily work. And luckily so! Im not bound and fixed to the standard model. — Prishon

You can’t both want to go public with your private theories and reject the rationale for that public approach.

Again, science is about making rash counterfactual claims in a completely public fashion - one framed with mathematical definiteness and so as little as possible wiggle room. Then the evidence is also public. We can all read off the numbers for ourselves.

Obviously you keep mentioning your pet theory that speaks of the Cosmos as a 4D torus in a 5D space that spits out 3D rishons. It sounds a bit mathematical. But is one a Euclidean manifold, the next a material field, the final step a spray of particles? What kind of “not even wrong” confusion of words are you throwing together here - even if it is very easy to see the labelled diagram of three kinds of shapes you likely have “in mind”.

Sure, I can visualise a drawing of a flat manifold with a hovering torus and jets of “rishons” and “anti-rishons” spurting out from both sides of its Janus-arse. Your word picture is constructible. But that ain’t sufficient proof it is true, let alone that it has the necessary logical structure to be making any grand claim about the Universe.

Talk about primordiality to analytic philosopher and you will get only blank stares. — Constance

How are you defining “primordial” exactly? Is it an abstract term with some concrete meaning, or just a ritualistic and impressive noise one might make - a group identifying chant?

Which raises the question for both materialist physicists and non-materialist meta-physicists, "what caused that sudden symmetry break . . . that instant imbalance?" — Gnomon

The Universe was also expanding and cooling at an exponential rate while in that vanilla unbroken state - according to the simplest extrapolations. So the Universe just had to cross a threshold where the unified conditions finally broke in the usual phase transition way. Or not so usual if this breaking also released an inflationary spurt.

Admittedly, the latter is not an empirical scientific theory, but then neither is the imaginary Quantum Fluctuation scenario. So, why not give due consideration to both propositions? :cool: — Gnomon

But GR and QM are empirical. Phase transitions are empirical. Everything back to the Planck event horizon has at least an evidenced basis that constrains its speculations.

Even versions of teleology are empirical to the degree that quantum nonlocality and retrocausality are accepted as a thing - Jack Sarfatti offering an example of such a line of thought here.

So the reason to take one side seriously is that there is good evidence for its starting assumptions.

Which raises the question for both materialist physicists and non-materialist meta-physicists, "what caused that sudden symmetry break . . . that instant imbalance?" — Gnomon

An expanding and cooling space of fluctuations will at some point cross a threshold where the fluctuations cease to rule as correlated actions start to take over. The simple example is steam condensing into water. So order emerges as all the hot particles become regulated by some larger collective state. Lawfulness appears. It is almost as if a divine hand intervened … not. :razz:

So in general, once you have a Planckian world with the ingredients of spacetime and energy density, the future is baked into that material package. The puzzle - the need for new physics - lies in how to account for that starting point.

My own points here is about taking the emergence of spacetime and energy density seriously and looking for some kind of naked symmetry breaking story which produces that initial division itself. Don’t just keep shoving that basic step further back in “time” to some other “place” that has “infinite” energy to expend. The next step for cosmology has to be the one that breaks down the very notion of dimensionality and gives it an emergent explanation.

This is why loop quantum gravity was a promising approach. Many different versions were at least suggesting that naked 1D fluctuations - an action without a space to give it direction - could still knit together a web of correlations. A quantum foam would find its own emergent order that cooled its chaos. There was evidence for the speculation in terms of running computer simulations of the maths being proposed.

Materialist approaches also can claim to know what are the known unknowns. The key to unlocking progress is figuring out the grand unified symmetry that describes the Plankscale initial conditions - the one that unifies the Standard Model’s hierarchy of known symmetry breakings.

So the materialists have a pretty well defined project ahead of them. The issue of what came “before” the Big Bang is interesting. But there are big gaps to fill in the story of what the initial symmetry state looked like first.

Scientists tend to prefer a physical scenario, such as the Quantum Fluctuation hypothesis (due to random Chance). And some Philosophers prefer to consider a non-random lawful scenario, such as Aristotle's First Cause/Prime Mover (a deity of "pure form"). Which acts via teleological Intention. — Gnomon

My own approach is influenced by Peircean systems logic. And that would argue that the initial conditions were a vagueness - a “realm” where the principle of non-contradiction had yet to even apply.

So law and fluctuation would have been indistinguishable to the degree that both were present. They would have “existed” as just the latent possibility of such a division.

And this is what the reciprocal structure of the Planck constants tell us. At the beginning of the Big Bang, fluctuations had the Planck temperature and so were as big as the spacetime world they were happening in. The buckling effect of the hot contents was equal to the confining impact of its would-be container. There would thus be both law and chance in balanced existence, but right on top of each other in sharing the same scale, and so not yet actually distinguishable as two divided aspects of the one larger reality.

The Big Bang is the birth of the division and growth in scale that increasingly locates chance to the local scale of being, and law to the global scale of being.

This is why the Universe seems so perfectly divided in its era of Newtonian classicality. There is a rule by global law. And that allows the writing of prescriptive equations into which any "chance" measurement can be inserted as a local variable.

Chance is so constrained that you can count it as entropy, or distinguishable microstates. The only real fluctuation is quantum, and that has been tamed by decoherence now. Just as law has been pushed so far towards its global limit that it appears to transcend our Universe (becoming written in the mind of God so far as many materialists are concerned :smirk: ), so too chance has been pushed to the edge of the cosmological picture - and thus led to pathologies of extrapolation such as the many worlds interpretation of quantum theory.

So yes. We can boil it down to metaphysical first principles like the dialectical opposition of law and chance. But then we want to avoid the chicken and egg debates about which came first, or which is the ground to the other. That is the kind of causal logic that sets up the two sides of the one story as disjunct monisms. Both good old fashioned materialism and good old fashioned theist woo (or idealism) are logically in error because of their shared reductionism.

It is written into the Planck constant derived equations that describe spacetime and energy density that the logic is dialectical or reciprocal. Local chance and global law are themselves the two sides of reality that had to co-arise as a unity of opposites, a symmetry breaking that was self-organising. You have the triad that is the h that scales pure fluctuation or energetic curvature, the G that scales any deviations from global flatness, and then the c that is the scalefactor for their ever expanding and cooling trajectory towards their respective asymptotic limits.

This kind of logic ought to be very familiar for anyone who has studied ancient Greek metaphysics, or even Eastern approaches like Taoism and Pratītyasamutpāda. In more recent Western tradition, we have Hegel and Peirce.

But as it happens, even a central loops thinker like Rovelli can write an enthusiastic book about Anaximander as the first scientist ... and miss the essential metaphysical point ... of what Anaximander meant by ... apokrisis, or "separating out".

I don't really have any objection to any of this — Seppo

If you're going to be so damn reasonable then I have to rescind that dogmatic comment. Bugger. :smile:

If the current projects/paradigms (string theory, supersymmetry, etc) were going to bear fruit, you would have hoped it would have happened by now... and that just hasn't happened, we've been spinning our wheels for decades. — Seppo

Yep.

I tend to be a bit more conservative in sticking to what is the widely held view of people with actual formal expertise on the subject, hence my comments here sticking to what I guess is sort of the party line on the topic RE quantum gravity and early Big Bang cosmology. — Seppo

Again, that's fair.

It it just that the party line too often feels like the party members papering over their own divisions and confusions so the general public/taxpayer funders don't catch on to what a mess they might be in.

In fact I parked particle physics and cosmology a decade ago to give them time to catch up with themselves and see if some actual new consensus might emerge. Loop and condensed matter approaches were encouraging at the time, but also starting to fall apart like strings did.

I think what did it for me was the loop guys suddenly promoting bounce cosmology as the kind of "theory" that a new multi-billion euro collider might just be able to test. Suddenly there was a new party line to be built around a ginormous funding application ... and let's not look too closely at its scientific merits.

But in case you are interested in where I am coming from, there was this really good blog post by the "Hammock Physicist", Johannes Koelman, in 2010. He was so on the money for me that it was no surprise he appeared to give up his academic ambitions and turn to making a living in industry soon after.

http://www.science20.com/hammock_physicist/physical_reality_less_more

I wrote up a precis at the time which I can simply paste here just in case it has value.

Preamble: Most modern metaphysics presumes the laws of reality, the structure of the cosmos, to be contingent. The laws are just whatever they are with no real explanation other than some kind of anthropomorphic accident. This is a view that drives Tegmark and his multiverse speculation and other expressions of modal realism.
But physics itself appears to be closing in on a tale of mathematical necessity, a tale of symmetries and symmetry breaking, which now in metaphysics is also inspiring new schools of thought like Ladyman and Ross’s ontic structural realism - http://www.amazon.com/Every-Thing-Must-Metaphysics-Naturalized/dp/0199573093
So this is a new “emergent Platonism”. It is not that there is a realm of infinite forms – a Platonic ideal for every possible particular entity from triangles to jam jars – but rather that there is a general mathematical inevitability to the structure of nature. Given a starting point of unlimited material freedoms, some kind of prime matter, apeiron or entropic gradient to shape, a world must then self-organise according to certain intelligible principles. And this is what fundamental physics has quietly been doing from Newtonian Mechanics right up to string theory and loop quantum gravity today – systematically following the path leading back to the deep mathematics, the ur-pattern shaping nature.
So this is post about the unification of physics project. And this excellent blog post by Johannes Koelman gives the guts of the argument - http://www.science20.com/hammock_physicist/physical_reality_less_more
I will use it as a jumping off point, particularly this Venn diagram of how the theories form a three-cornered hierarchy of generalisation....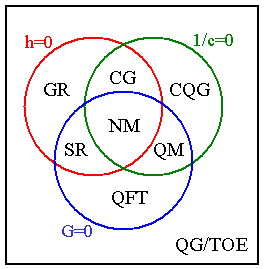

Planck constant triad: Where does it all start? With the idea of symmetry and symmetry-breaking. Or the birth of scale, the birth of difference within what was “the same as itself”. And so it is about a special kind of reciprocal dualism or asymmetric dichotomisation where the same becomes different by moving away from itself across local~global scale.
Now this is an unfamiliar idea to most even if it is very ancient – the basis of Anaximander’s cosmology, the very first true metaphysical system. But briefly, it is about inverse relationships. If you take a classical metaphysical dichotomy like flux~stasis, chance~necessity, discrete~continuous, etc, you can see how each pole defines itself as the reciprocal of the other. Stasis is the state where there is no flux, or the least possible flux. So stasis = 1/flux. That is, the larger you imagine flux to be, the smaller or more fractional the quantity of it you will find within stasis. And the converse applies. Flux = 1/stasis. The larger the amount of “no change” imagined, the less of that there is to be found in flux, and so the more “changeable” flux becomes. All regardless of any actual measurement or quantification.
So this is a special mathematical relationship that emerged in Ancient Greek metaphysics – the dialectic manoeuvre that drove its speculative twists and turns. And it has re-emerged centre stage in modern physics as symmetry-breaking and the various dualities or complementary relationships that are a feature of high-level theories.

Now on to those theories. As Koelman makes clear, it starts with Newtonian Mechanics (NM) where the local~global relationship, the primal dichotomisation of physical scale, was first properly quantified – but in an actually broken apart way.
NM presumed a fixed space and time backdrop and then defined the rules for quantifying local events within that absolute reference frame. That 'broken apart" classical view of nature certainly worked at the human scale of observation, where we are so far from the bounding limits of the cosmos. But as science developed particle accelerators and radio telescopes, physics had to expand its view too. It had to develop post-classical theories that included an account of the global container as well as the local contents.
And in brief, that has turned out to mean bringing a triad of "dimensionless" constants inside the picture we have of reality – the three Planck constants of h, G and c. (h = Planck’s constant that scales the quantum uncertainty of things, c = the “speed of light” or the constant that scales causal interaction, and G = Newton’s gravitational constant that scales mass/spacetime curvature.)
There are only these three critical “numbers”, all somehow tied to the most fundamental level of symmetry-breaking. And with NM, we start with them all outside the physical theory as values that have to be empirically measured – which is an immensely tricky and approximate story in itself. Then the story of modern physics has been about pulling the constants inside the theories, first in ones, then in twos, and finally, hopefully, with the ultimate Theory of Everything (ToE), getting all three inside the picture of nature together at once. At which point, physical theory would become completely rational, drawing up the ladder on the need for empirical measurement as the mathematical structure would be able to account for itself entirely.
This is because the constants will have been defined in the same self-explanatory way as the old metaphysical dichotomies like flux~stasis. The constants represent the action that breaks a symmetry, but now in both its “directions”. Asymmetrically or reciprocally across actual hierarchically-organised scale. What this means should become clearer as we see how physics has developed since Newton.

Newtonian Mechanics: As Koelman points out, NM was based on reducing the empirical measurement of reality to four quantities – distance, duration, force and inertia. The brilliant idea at the heart of scheme was to disconnect the local scale from the global scale by imagining the global scale to be a fixed, flat and eternal, backdrop. Space and time were made a static symmetry – you could go backwards or forwards in space’s three global dimensions or time’s single global dimension and they “didn’t care”. It was all the same, and so symmetrical.
This was of course a view of nature directly inspired by Ancient Greek atomism and its notion of an a-causal void, where similarly, all causality, all action or symmetry-breaking, involved local parts. Only material/efficient cause was real, making formal and final cause a fiction projected onto the emergent regularity of atoms contingently at play. And given that space and time were defined in this absolute sense – a matter of brute and immutable fact – this legitimated the use of clocks and rulers as universal measuring yardsticks. You could create a standard unit of distance or duration because such a human construct was underpinned by the concreteness of space and time themselves. At any place, in any era, and at any scale, these clocks and rulers would continue to function reliably because they were measuring something unimpeachably real.
So Newton – as a metaphysical premise – created an unchanging backdrop against which the kind of change we are most interested in, the middle-scale realm of lumpy objects, could be crisply measured. Now he only had to model a localised symmetry-breaking – the one between mass and force, or between the material property intrinsic to a body and the web of interactions between such bodies. This led to his three laws of motion.
Newton's first law defines the inertia of bodies. Massive objects can have a "resistance to change" in their motion if that motion does not break a global symmetry. So a ball can roll forever in a straight line due to translational symmetry, and it can spin forever due to rotational symmetry. The combination of mass and velocity gives a body a momentum value. A force - as then defined by the second law, F=ma - is a change in momentum imposed from without. Like by getting smashed into by another object. With absolute space and time as a fixed reference frame, these "hidden" local quantities of force and inertia could be read off the world in terms of localised symmetry breakings - a curving path or a change in velocity.
Then Newton’s third law of action~reaction restored the broken symmetry by creating a global energy conservation principle. Everything that got pushed, pushed back equally, leading to a net zero force at the global scale. Nothing happened to disturb the static stage upon which the mechanics played itself out.

Newtonian gravity: It was a neat system. But of course it only dealt with objects banging into each other. And Newton had to make another big leap of the imagination to deal with gravity – a global force that “acted at a distance”. His peers like Descartes had tried to make sense of gravity’s pull as a jostling of spatial atoms. The sun and planets were swirled around in circular orbits because they were caught in the flow of super-fine corpuscles. But Newton boldly posited gravity as an intrinsic property of mass. And one that scaled (inversely!) with distance. The greater the separation, the more weakly the gravity of a body was felt.
So Newton again used an absolute backdrop as a way to localise the notion of an action – the material cause of change, the thing that breaks a physical symmetry. And as the other forces like electro-magnetism became recognised, the same general mechanics could be used with them as well. They could be quantified as vectors – a small push or pull in a direction acting to disturb the inertial motion of a body.

Post-Newton theory: The Newtonian model worked so well because it homed in on symmetry-breaking on the human scale - where we are 33 orders of magnitude distant from the smallness/hotness of the quantum scale and 28 orders of magnitude away from the bigness/coldness of the visible Universe, the relativistic scale. Action or change might be taking place at the extremes of scale, but the Universe would still look a flat and unchanging backdrop because either the change up at the relativistic limit was so large and slow that it was beyond our field of view, or equally, down at the quantum limit, so small and rapid that it become an unbroken-looking blur.
But eventually it was realised that the Universe was dynamical over all its scales. For one thing, it was born in a Big Bang and is spreading/cooling towards an entropic Heat Death. So the extremes of scale had to be brought inside the general model and made subject to the same laws ruling change.
In prescient fashion, it was Planck in 1899 who saw that all mechanics could be boiled down to three constants – three dimensions quantifying the actions that break even the most global symmetries. Well, Planck thought it would be four as he included Boltzmann’s constant, k. But by the 1930s, Matvai Bronstein had clarifed that physics was looking for the magic trio of cGh. Well, in fact to show that it is only retrospectively that physics understood the deep logic of its own progress, the much more famous names of Gamow, Ivanenko and Landau cooked up this little insight as at first a joke, allegedly to impress a girl, and then 50 years later, Okun, another Russian rediscovered it and finally popularised the way cGh anchored all physical theory as “Okun’s cube”. Here are a couple of blog posts on this history.
http://backreaction.blogspot.com/2011/05/cube-of-physical-theories.html
http://blogs.scientificamerican.com/guest-blog/2011/07/14/why-is-quantum-gravity-so-hard-and-why-did-stalin-execute-the-man-who-pioneered-the-subje
So OK, it was not so obvious at the time. But it does explain why physics ended up organised like Koelman’s Venn diagram, a systematic attempt to turn three empirical and apparently arbitrary measurements into three reciprocally self-defining and so mathematically necessary global symmetry-breakings.

Special Relativity: Ticking through these quickly, first came Einstein’s Special Relativity (SR) which incorporated c into mechanics as a general yo-yo factor.
First space and time (representing stasis and flux in terms of locatedness and change) became glued together to become the one thing, a global scale symmetry balance that Koelman dubs “spacetime-extent”. Then c scales any breaking of this balance with extent multiplied by c = distance^2 and extent divided by c = duration^2. So in this way spacetime is changed from being a static backdrop to a dynamic dimensionality where the baseline of “no action” is effectively redefined as the expanding sphere of an event horizon. Events are physically separated by a distance and a duration in the way that the sun may have vanished four minutes ago, but it will take another four minutes before we can know about it. So to break spacetime in such a way as only to see “a distance”, you have to multiply by c to allow “enough time” for the distance to “happen”. And conversely, to recover “a duration”, locate it within a purely temporal dimension, you have to divide by c to remove the space over which it has has spread.
A simpler way to understand this is considering spacetime from the points of view of a massive particle and a light ray. Even if it is stationary, not moving in space, the particle is now moving in time. It is “travelling” into a future where the distance to any event horizon is getting constantly c-times more expanded. And conversely, the light ray may be moving at c through space, but now – being already “at” the event horizon – it is “stationary” in respect of the global dimension of time. So there are two ways to be standing still and two ways to be moving. And which way round you read off the symmetry breaking is scaled by c or 1/c.
Thus globally, spacetime was scaled by a reciprocal action. Then locally, the same was done to the Newtonian version of the action. Energy and momentum became glued together as a “general stuff” – spacetime-content – and this symmetry again broken by a yo-yo inverse relation. By E=mc^2, mass could be converted into a “times-c” amount of energy, while energy could be converted into a “times-1/c” amount of mass. The material contents of the Universe could be viewed either in terms of an energy density located to a spatial point, or smeared across a temporal sphere. The two were dichotomous ways of looking at the same thing. So “where you were” as an observer within the system had to be specified by an inertial reference frame if you wanted your Newtonian rulers and clocks to read off the same distances and durations. Nothing was absolute, but in a dimensionless way, you could still distinguish c from 1/c as the generalised limits on reality.

General Relativity: SR incorporated one of the three Planck constants, c, but left out h and G. So the quantum uncertainty and gravitational curvature of the Universe remained “measurements from outside” the system being measured. This didn’t matter outside the middleground scale of classical objects – lumpy masses bumping about in a cool/large void. But it did matter if SR was going to continue to measure the world accurately as it approached these two other limits of nature.
Einstein of course took the next step of extending SR by incorporating G alongside c to give General Relativity (GR). Spacetime was now made bendy, defined in local fashion by its energy density. Instead of distance and duration being flat and even dimensions – Euclidean as presumed by Newton – they were free to adjust their geometry according to the density differences in their material contents. Or being a bit more technical, spacetime and its contents became unified as flipsides of the same thing – the Einstein-Hilbert action. The reciprocal nature of the deal was again made explicit in the maths, spacetime being scaled by G/c^4 while the mass/energy contents was scaled by c^4/G.

Quantum Mechanics and Quantum Field Theory: The other big revolution going on was Quantum Mechanics (QM). It had been discovered that reality is scaled by an uncertainty relation – a yo-yo deal centred on h as its “physical” value. In QM they called this complementarity, making the connection with Eastern metaphysical thinking like Yin-Yang (which of course is another version of the same thing the Ancient Greeks were talking about with dichotomies). But anyway, what QM said was reality is fundamentally vague or indeterminate.
Measurements need to be made from a fixed point of view to have definiteness. And when you get down to nature’s essential symmetries (and the asymmetries that break them in local~global scale fashion) then trying to pin down one end to a crisp value sends the other off to unknowable indefiniteness. So ask about a particle or event’s position and its momentum goes off the other end of the scale. Zero in on it in terms of time, and its energy could have any value.
By including this yo-yo measurement issue in the physics, QM made explicit the way classical mechanic had been coarse-graining reality. When things are cold and large – far from h as a limit – then the Newtonian picture works well as reality is near to dammit determinate in its behaviour. But approach the complementary limits of the hot or the small, then the classical crispness breaks down in a well modelled exponential fashion.
So QM pulled h inside the mothership of Platonic physics, but like SR, it left the two other constants dangling – c and G. This was fixed by Quantum Field Theory (QFT) which repeated GR’s trick, this time combining h and c.
QFT is a relativised version of QM and it did this by treating particles as excitations in a field. So there was the jump from a Newtonian strict location of a symmetry and its breaking (a particle, its properties, the forces that might impinge on it) to a field view where everything becomes global and contextual. The key calculational breakthrough was Feynman’s concept of path integrals, or sum-over-histories. Uncertainty could be quantified as all the paths that a particle might have taken quantum mechanically and then the path “actually” taken as the shortest possible path to get where it got. So all the energy values the particle might have had (given the scale of the action) could be averaged across. And relativistic effects, like what speed does to mass and time, could be included as contributions to the final result as well, giving a picture of an action zeroed to some definite reference frame.

Cartan Gravity: SR, GR, QM and QFT are the familiar fab four. But far less well known is that there is a third leg to this story of the grand consolidation of the theories. As Koelman points out, logic demands there was also Cartan Gravity – an effort to match SR/c and QM/h with a generalisation of Newtonian mechanics that dealt solely with G. And then following that, even a Cartan Quantum Gravity that unified G and h.
Now the Cartan notion of space is based on torsion (as opposed to say curvature). But I confess I am not clear why it is not a big deal like quantum and theory and relativity. Perhaps combining G and NM has little technological value (QM especially has been the basis of valuable everyday application). Certainly Newtonian gravity deals with the classical scale of interaction perfectly adequately given that massive gravitational fields are not the kind of thing we can bring to bear on nature in the same way we can with c or h scaled phenomena.
Anyway it is said Cartan theory may yet come into its own as the basis for loop quantum gravity or other ultimate theories where forces have to be modelled as twists in space. And certainly it is a necessary third leg of the theory unification process. It is logical that this way of climbing the same mountain also is possible.

Theory of Everything: So that then just leaves one final step – a ToE or Quantum Gravity (QG) theory that hoovers up all three Planck constants, cGh, into the mothership of reciprocal dimensional maths.
As Koelmans says, this seems to require a further extension of the sum-over-histories approach where QFT is enlarged to include G or spacetime curvature. As well as averaging across the uncertain energy levels of a particle and any global relativistic contributions, the calculation would have to average across any local uncertainty in the spacetime the particle is meant to be travelling through (or the excitation and the field it is “happening” in). QFT can in fact give approximate answers of that kind by imposing a cut-off on local gravitational contributions, but a properly elegant way of doing this – one which shows how the three dichotomies can be both internalised and also connected to each other as some kind of fundamental geometric relationship – is still a work in progress.

Planck probably thought that by calculating the smallest possible measurable time or length, that fades into asymptosis or ellipsis, would put an end to such "before the beginning" nonsense. — Gnomon

Planck was actually just thinking about the problem of why the heat radiated by an object didn’t add up to infinity like a simple extrapolation of know physics said it should. He introduced the notion of a quantum cut-off point. That ushered in physics’ next big paradigmatic revolution.

So that should tell us something about the need to avoid infinities if we are to have the bounded finitude we actually observe as our natural habitat. Existence is a limitation on too much everythingness. Creation is not about getting something out of nothing but of developing constraints on unbounded fluctuations.

I believe Anaximander said something along those lines 2500 years ago. Indeed, all pre-modern cosmologies seem to be the same creation story of order arising out of chaos.

Put together Planck’s h, Newton’s G and Einstein’s c to make Okun’s cube of physical theories and you have a model of a mechanism where the positive curvature of quantum fluctuations is balanced by the negative curvature of gravity at a rate that is scaled by the speed of light. We have a set of fundamental constants that are cast in a dialectical or reciprocal relation with each other.

So we discover there is this broken symmetry at the root of things. It is not unreasonable to wind that back to the symmetry state that marks its beginning.

Metaphysics has always reasoned this way. But modern thought - on both sides of the realist-idealist divide - has gotten into the habit of simple reductionism and it’s cause and effect monism. Creations can’t be self-organising say the reductionists. They demand a creator that stands outside the creation.

It would be nice, if for a change, we could just freely speculate on such pre-columbian "what's out there over the horizon?" scenarios, without coming to blows over which party is the biggest idiot : the short-cut-to-India optimists, or the sail-over-the-edge-pessimists. — Gnomon

That is true. But also, there is ample science to constrain the free speculation. Yet then cosmology is like quantum theory in that scientists themselves go crazy with their speculation as they have not invested too much effort in questioning the reductionist habits of thought that have generally made science so successful.

That makes it an interesting situation - like consciousness studies too - where those who are very well informed about the material facts are also blinded by the paradigm within which those facts were developed. Both the well informed and the uninformed can make dogmatic assertions about the nature of the Cosmos and the nature of the Mind that are ill thought out for their different reasons.

The prevailing view (the dogma) is that space can't be embedded in a higher dimensiolal one. But thats questionable, although the dogma forbids asking this. But 3d space can be immersed in 4d space. Causing expansion to be an illusion. — Prishon

You have clashing brane theories that make use of string theory’s higher dimensionality. So this is another example of reductionist desperation in my eyes. But mathematical physics is certainly not dogmatic about these kinds of things.

The Ekpyrotic Model of the Universe proposes that our current universe arose from a collision of two three-dimensional worlds (branes) in a space with an extra (fourth) spatial dimension.

But there are good reasons for just 3D, like the fact that gravity and other forces aren’t leaking away into this embedding space. They weaken at the square of their distance and not the cube.

And more to the point, cosmology noticed that all the stars become increasingly red shifted with distance from us. So unless the Earth is the still centre of an exploding creation, you have to accept the conventional Big Bang cosmology.

No, it's flat and Euclidean. — frank

You might be thinking just of space and not spacetime. Inertial expansion is flat but accelerating expansion is curved.

As I said, the prevailing view now is that there was no singularity of any kind. Big bangs happen from time to time in a greater universe that could be without limits. — frank

But even Linde’s eternal inflation is a story about a fractally branching multiverse so it indeed all branches from one initial starting point. There is a singularity in the need to explain why there was the first Planckian shoot that became the vast tree.

But if I had to pick a pre-Bang cosmology, an inflating multiverse seems the best candidate. It at least provides an anthropic reason why we live in a branch that happens to have the “right” randomly chosen physical constants - I mean all the constants besides the three key Planck ones the multiverse must also presume. :grin:

But I do object to the suggestion that there's anything "dogmatic" about pointing out that the parts of the BBT which are widely-accepted and observationally-corroborated don't include any beginning or origin of the universe. — Seppo

The dogmatism relates to the assumption of a beginning/origin having to exist at some smaller scale/hotter temperature beyond the Planckscale event horizon of the Big Bang.

Spacetime and energy density are so yoked together that going "smaller" and getting "hotter" really doesn't make sense if curvature reaches its maximum at that scale. We arrive at a "just before" that is all blackholes and wormholes – a quantum foam at best.

That might be still a "something" we can model as a pre-Bang state. It just wouldn't be any kind of time, place, or state of materiality, as we claim to know it from this side of the cosmological event horizon.

So the Big Bang would in that view be the start of the Universe in the sense that the term has any useful meaning.

After all, I'm sure you would agree with the conventional reply when folk ask what is the Universe expanding into. Very quickly you will say it is just the expansion of the metric itself. The Universe is not embedded in some larger space.

But why doesn't the same logic apply to the origin of the Universe? Why does it have to be developing out of something? Why can't the development itself be what produces a developed something?

My only purpose is to counter the familiar and misleading talking point (found mostly in popular-level content on cosmology/BBT) that this is a generally accepted or observationally well-established part of the standard cosmological model accepted by most cosmologists, or that the BBT is primarily a theory of the origin of the universe (rather than of its development). It just isn't. — Seppo

I'm trying to highlight the problem with what you say is the generally accepted metaphysics.

It could be the case that Universe didn't start at the "point in time" that is its Planckscale event horizon. It could be true that there is a lengthy pre-bang story along the lines of Linde’s eternal inflation or Big Bounce cosmology. It may well be that QG is a theory that sees beyond the Planckscale and finds some kind of spacetime/energy density story that pushes the origin of that spacetime/energy density story into realms that are simply just smaller and hotter.

But these ideas are speculative, simplistic, and don't even tackle the essential questions about why there are these things of spacetime and energy density. Again, we pull folk up who ask what space our Universe is growing into, yet seem untroubled by bouncing cosmologies or branching inflation fields that presume a familiar notion of passing time as the place in which our Big Bang universe appears as just another material development.

Nothing useful is added by these kinds of linear extrapolations. The question is why spacetime and energy density are even a thing that came into being. Telling people not to bother so much with the Big Bang, wait for the full story of the "universe" beyond the Planckscale, is buying into the bad metaphysics that simply makes good careers for mathematical physicists looking to stay relevant in a time where there is little actual progress to report.

My inclination is instead to turn things around, take the Big Bang seriously as its own origin point, and see how that fits what we already know in terms of GR, QFT, the Planck triad of constants, and general symmetry breaking and condensed matter physics principles.

The Planckscale describes the first moment when spacetime as the backdrop, and energy density as its contents, could be told apart. It's a tale of co-dependent arising. And that is already the story the Big Bang theory tells in its talk of a beginning that was a relativistic realm of vanilla GUT force fluctuations. In what sense did either distinct particles or a background vacuum exist when the world was still so hot that the void was completely filled by its own wild fluctuations? Big Bang theory then says that was the initial lack of proper separation that became fairly quickly an expanding~cooling process of increasing separateness.

You don't have to like the scenario. But again, the point is that we agree not much progress has been made these past 20 years or so. Conventional thinking might be that we just need to be able to punch through the Planckscale event horizon to discover what further cosmological structure lies beyond its veil. I say the event horizon most likely simply marks an actual limit on counterfactual being. And that is at least an alternative worth being discussed - as has indeed happened with some of the loop and condensed matter models.

They've actually looked to see if the universe shows overall curvature, and it doesn't. — frank

But they looked and found it has dark energy and so an "internal pressure" that means spacetime isn't contracting, nor even coasting to a gravitational halt, but is undergoing open-ended acceleration.

So there are three generalised curvatures the Universe could have had - closed and hyperspheric, flat and Euclidean, and open and hyperbolic. The surprise is that it looks to be hyperbolic and so the event horizon of the Big Bang can be matched by its inverse of the event horizon of a de Sitter space Heat Death.

The end of the Universe is also a problem. It was hard to believe it could actually be so finally balanced in terms of its gravitational contraction and thermal expansion that it might indeed just coast towards a stop over infinite time - another singularity! And if it had too much gravity, too little matter, then it is almost just as improbable that it would have lasted the 14 billion years until now without collapsing.

So a faint positive curvature allows the Universe to stay open and yet come to an eventual Heat Death halt in terms of its cosmological event horizon – the size of the region that counts as the observable Universe.

The source of that dark energy or cosmological constant still has to be explained. It would be nice if the simple theory - that it is curvature contribution from the quantum fluctuations of the vacuum itself - pans out. That would make the force something internal to the fabric of spacetime itself - all part of the Big Bang deal.

That's the prevailing view in physics right now. No singularity. — frank

Well singularity is a technical term in maths for some kind of radical break or discontinuity in the smooth continuity of a function. So it can take many shapes.

Folk who were rewinding the GR-regulated evolution of the Cosmos past the Planckscale were aiming at a singularity shaped like a zero-D point. They wanted to shrink things to where spacetime was infinitely small. But QM said that meant it also had to be infinitely hot - as such complete certainty about location was a matchingly complete uncertainty about momentum.

But actually tie to the two curves together by inserting all three Planck constants into your cosmological equations - as QG would have to do - and you get instead (hopefully) a smooth transition in terms of a singularity-masking event horizon.

we need a quantum theory of gravity to describe what is happening... which we don't have. So we can't rewind any further, as we have no description of how physics works in those extreme conditions. — Seppo

Do you see how you just confused the expectation of being able to rewind (in linear fashion) beyond the Planckscale event horizon with the acceptance that it is the actual limit of such rewinding?

You have been very dogmatic about the Big Bang not counting as the actual beginning of the Universe, but that is just a failure to rid your metaphysics of this assumption about linearity - the ability to extend any straight line to infinity.

What QM tells us about GR is that its straight lines become eventually so completely curved that they turn into little circles. You wind up with a description of a spacetime foam that is populated by blackholes and wormholes. A mess of naked and disconnected fluctuations, in other words.

So the Universe - as we understand it to be, via our models - is this classical realm dominated by its Euclidean flatness. We then look a little closer and have to come up with further models like GR and QFT that introduce some curvature and uncertainty. Then we track those speed wobbles in our initial Newtonian determinism and find eventually it all goes completely out of control. All the straight lines turn into curves so tight they are a foam of circles. All the uncertainty becomes so great that all that exists is naked fluctuation with no grounding context.

QG might be regarded as a project that restores linearity to the physics in a way that will let us punch right on through the Planckscale event horizon and see what lies "beyond" ... as some extrapolatable continuation of a spacetime extent and its energy density content. But as with the Hartle–Hawking imaginary time proposal, everything we know and love as the metaphysically taken-for-granted might just curve into each other and thus vanish up its own collective arse. :razz:

So the problem lies with projecting linear expectations onto GR and QM, which are already themselves frameworks for dealing with the gathering curvature and uncertainty of reality, and then expecting QG to be the triumphant return of Newtonian straight-line metaphysics.

GR works because it uncouples the connection between spacetime extent and local energy density. So in a Universe that is generally large, cold and empty - which means what, about at least 10^-10 seconds old and down to barely 10^15 degrees? - the two halves of the one reciprocal deal can seem clearly separated. You have a backdrop of flattish spacetime in which reasonably well located events are taking place. The electroweak symmetry has cracked. The Higgs field is on. Particles now have a mass that means they can go much slower than light, even if they are still a long way from being at any kind of rest.

But as we wind the clock back towards the Big Bang, we see all that familiar asymmetry being swallowed up into the anonymity of an increasingly more general set of symmetries, until we arrive at a vanilla GUT force and a matchingly vanilla notion of a relativistic quark-gluon soup, just before everything merges into the one cosmic vagueness of an event horizon, beyond which lurks only our notions about a quantum foam of fluctuations that could also be described in GR terms as a host of tiniest possible circularities - a hot mess of spatial blackholes and temporal wormholes.

So quit holding out hope that a QG theory will restore linearity and so discover a time and a place (and a higher heat or energy density) that lies over the well-demarcated Planckscale event horizon. That will enable you to be less dogmatic in your proclamations about the Big Bang not marking the beginnings of metaphysical linearity as we know and love it. The Universe that is generally large, cold and just about empty. :smile:

What bothers me is why did cosmologists stop the extrapolation at, to quote Wikipedia, "...hot dense state..." They could've simply drawn the trajectories of all the galaxies back to a point just as William Lane Craig and I thought. It's not that there was a law against it, right? — TheMadFool

But it makes a big difference whether you are imagining extrapolating a line - a linear relation - or instead an asymptotic curve.

Do the two parts of the cosmic equation - spacetime extent and energy density content - go to infinite value because they trace back all the way through the Planckscale event horizon and meet at a point, the confounding singularity, at some further distance beyond?

Or are the two parts of the equation yoked to each other in reciprocal fashion - as the Planck triad of c, G and h suggest - so that instead they converge asymptotically to create that event horizon that marks the beginning of both spacetime extent and its entropic spreading.

After having now read a number of papers discussing Peircean semiotics in the context of a range of approaches within philosophy and psychology here are my tentative thoughts: — Joshs

It’s a good post. You set out the positions clearly. :up:

The second school is the pragmatism of Dewey, James and Mead, which , while sympathetic to Peirce’s approach , avoids the strict logic of his code-based semiotics in favor of an intersubjectively mediated empiricism. — Joshs

Yes. But my reason for championing Peirce here is his tight focus on the semiotic modelling relation and the mechanics of codes. This is key because what is generally missing from causal metaphysics is an account of how the two realms of mind and matter interact. Semiosis plugs that explanatory gap.

Peirce himself is pretty weak on how semiosis in fact applies to biology, neurology, psychology and sociology. His own phenomenology, or phaneron, just tries to shoehorn things into a trite trichotomy of faculties - feeling, volition and cognition.

Similarly, his agapism is toe-curling. He was mired in the theism and transcendentalism that was the norm for his cultural milieu.

But on the central issue - the generality of semiosis as a mechanism to connect the two divided aspects of nature - he is sound.

Their notion of semiotics is not code or logic based but instead compatible with Wittgenstein’s language games as forms of
life. They reject the concept of language as ‘meaning’ , of truth as propositional belief, and critique empiricism and the myth of the given. — Joshs

That’s fine. But my reply is that this is the view from just the level of semiosis that is language use, and so just the aspect of human psychology that is socially constructed,

My interest is in countering scientific reductionism and its idealistic counter-response, romanticism, with a systems or natural philosophy metaphysics - the tradition that traces itself back to the four causes of Aristotle.

This view is well developed especially in theoretical biology. As I have described, I was focused first on the socially constructed nature of the human mind (so Vygotsky was my man there), then on neuroscience and philosophy of mind, then on complexity theory, then eventually - as the best unifying perspective I found - the circle of theoretical biologists led by Pattee, Salthe and Rosen. And these guys in turn were moving from a general hierarchy theory and modelling relations perspective to one that acknowledged Peirce as offering a unifying logical story.

But also, biosemiotics now goes far past Peirce in grounding itself not just on a process and probabilistic ontology, but the more specific one of the thermodynamics of dissipative structures. So there is a general theory where the material aspect of being is all about entropy dissipation (with the Big Bang being the most general example). And then semiosis and code explains how informational mechanism can evolve to accelerate entropy production. So the argument becomes that everything - from the Cosmos to Mind - is just a thermodynamic drive. And complexity arises out of that as grades of organismic semiosis.

This is a scientific claim more than a metaphysical one now. It stands or falls on the evidence.

Enactivism is generally thought as shorthand for 4E: enactive, embodied, embedded , extended and affective. The system is not simply embodied in its biology, it is equally embedded in its physical-social environment and extended into that ecology via tools outside the strictly determined end of the body
that are nonetheless part of its functioning. — Joshs

Sure. When enactivism came along as a vogue new term, it was already what I had always argued. But it lacks the emphasis on code as the hinge of everything. It is just a corrective to the general disembodied rationalism of Cartesian inspired psychology. It doesn’t count as an actual new paradigm. It only alerts us to fact that minds are part of the structure of the world - further steps up the hierarchy of infodynamics or Second Law constrained being.

As I mentioned before, there is almost no debate these days within phenomenological-pomo-enactivist circles as to whether being shaped is the source of selfhood. The only debate is over whether to jettison the notion of the subject entirely in favor of a social system with no independently identifiable parts, or keep some minimal remnant of the old idea of subject. I don’t think you appreciate how much more radically interpersonally based some of these approaches are compared with Peirce’s quaint-by-comparison code-based model of the social. — Joshs

Sure. This is what makes it unscientific and headed off into its own familiar culture game based on “othering” univocal discourse. If you can’t win the big game, you pick up the ball and go make your own games.

The question is whether the path of change today is leading the vanguard of psychological and philosophical thinking closer to Peirce or further away from him. — Joshs

I’m more interested in how this plays out for science - metaphysical speculation that is grounded in maths and evidence.

Does psychology even exist as a single scientific field anymore? I found it a mess of a discipline until I realised you needed to listen to those who focused on either mind at the level of the neural code, or mind at the level of the linguistic code. So neural cognition and social construction.

Those in many branches of the social sciences choosing to bypass Peirce’s semiotic form of pragmatism feel that a pragmatics is severely constrained when it is grounded in rationalistist logic and a notion of truth as a ‘real’ which is progressively attainable. — Joshs

So I should follow the crowd rather than follow the evidence? Hmm.

This grounding Husserl rejected. — Joshs

I don't see much rejection of the key thing that interests me here - a rejection of the primacy being given to a homuncular self, the first person point of view, the ego that grounds the rationalising after all preconceptions have been stripped away.

This is the fatal flaw - the one Peircean semiotics fixes. By focusing on the primacy of the modelling relation, both the self and its world become a co-construction. The two emergent poles of the one dialectical process.

This deals with Kant's epistemic strictures without then lapsing into the homuncular regress of a conscious observing ego sat behind the curtain. The "self" becomes just the fact that a set of habits are integrated from "a point of view".

Once psychology is understood as a semiotic modelling relation - one based on a mediating system of signs, and thus a code - then psychological science can get on with the interesting job of seeing the degree that two quite different levels of semiosis, biosemiosis and anthrosemiosis, play their part in shaping some individual psyche.

But if you don't question the central motif that is the dualism of world and ego, then you wind up down the same cul-de-sac as Descartes.

Maybe phenomenology is rescuing itself by a new stress on enactivism or embodiment. But that seems to be just the incorporation of biosemiosis so far. It doesn't appear to involve the socially constructed aspect of mind and selfhood - our enactive embodiment in a shaping cultural environment.

That is the PoMo-Romanticism having its effect. The driving idea there is to reject global constraints on local freedoms. To be shaped is read as being anti-self, rather than the source of selfhood in the first place.

So you are not yet convincing me that phenomenology is anything more than a passing curiosity in the history of ideas.

Enactivism itself is of course a crucial corrective to Cartesian representationalism. But Peirce already founds everything in that kind of pragmatic embodiment. And there are plenty of psychologists, from Helmholtz to Brunner, who got it as well.

As Thompson’s recent reappraisal of Husserl indicates, it was never phenomenology that trafficked in Cartesianism and representationalism, it was the early Anglo-American interpreters of Husserl who imposed their own bias on phenomenology. — Joshs

As I noted at the start, Husserl seemed surprisingly keen to contribute to this misunderstanding then.

No philosopher of the past has affected the sense of phenomenology as decisively as René Descartes, France’s greatest thinker. Phenomenology must honor him as its genuine patriarch. It must be said explicitly that the study of Descartes’ Meditations has influenced directly the formation of the developing phenomenology and given it its present form, to such an extent that phenomenology might almost be called a new, a twentieth century, Cartesianism.

Husserl E. (1964) The Paris Lectures

Speaking of Romanticism, let’s get back to Peirce. — Joshs

The original issue here was phenomenology’s roots in Cartesian dualism and representationalism.

Romanticism is then the more general dualistic response to Enlightenment materialism - an effort to appeal to the reality of the ideal and sublime.

Peirce’s is an anti-Cartesian view. He called it vicious individualism, among other things. He opposed both monism and dualism with his triadic systems epistemology and ontology - his pragmatism and his semiotics.

Peirce might follow in Kant and Hegel’s footsteps in developing their antimonies and dialectics into a full blooded story of hierarchical development. But he went way beyond in pin-pointing the mediating role of a sign relation that forges a self along with its world. As I say, he showed epistemology and ontology to be two versions on the one rational structure of relations.

The present argument is that he does not move as far from an Enlightenment rationalism as his more committed followers claim.’
(Andrew Stables)

Sounds awfully Romantic to me. — Joshs

So the conclusion is that Peirce is essentially still a rationalist - ie; argued a structuralist case. And you want to say that sounds like idealism-tinged metaphysics to you?

Cool.

You either impress or force. — Prishon

I can see you are certainly mucho impressed by your own arguments. But Newton likely had his reasons for distinguishing between vis impressa and vis insita, don’tcha think?

Like Aristotle, Newton in the Principia, refers to two kinds of forces: Vis insita, inertial forces which are seen as inherent to bodies and vis impressa, forces exerted on a body, such as pressure and impact forces.

https://spark.iop.org/history-force-concept

Unless tatologies make sense. You just cant take a force and impress it. The impression *is* the force. — Prishon

If you have a problem with the phrasing, best take it up with the dude that wrote the law. Tell him what a dope he is. :lol:

Lex II. Mutationem motus proportionalem esse vi motrici impressae,
& fieri secundum lineam rectam qua vis illa imprimitur.

Let Google be your friend….

An impressed force is an action exerted upon a body, in order to change its state, either of rest, or of moving uniformly forward in a right line. These definitions gave rise to the famous three laws: known as Newton's laws of motion.

https://www.iitg.ac.in/physics/fac/saurabh/ph101/Lecture3.pdf

No, their theologies were well ahead of their time. To the great bulk of the nonacademic culture that surrounded them , their ideas were generations ahead. — Joshs

First you lump and then you split, as suits your rhetorical convenience. Ho hum.

I thought logic was a cultural creation like the rest of philosophy. Isnt that the view of writers like Lakoff and Johnson, who view logic as embodied activity? I’ve read 5 or 6 different interpretations of Peirce’s triadic model and they all differ. You don’t think the variability in how people interpret ‘firstness’ has any bearing on the use od the logic? I think how much the application of his logic will differ from user to user depends on what they want to do with it. The more abstract and complex the aspect of the world one looks at , the greater difference interpretation will make. If you don’t see God in Peirce’a triad, you’re not looking closely enough. — Joshs

I’ve yet to see evidence you understand how it works. So not much to say here.

As with any thinker , ther are different Kelly camps. I happen to agree with those who align Kelly with pragmatism , phenomenology and constructivism. — Joshs

I’m surprised there is any kind of Kelly industry at all. He seems far too minor a figure.

The counterculture didn’t emerge as a substantial force until after Kelly’s death in 1967. — Joshs

True. But I was there and so in retrospect, it seems strikingly non-linear in the speed of the social transition. One minute, only the beats wore Levi’s. The next, jeans were the uniform. So a tension builds over time and then a phase transition results. One state of social conformity is replaced by the next.

Claiming that America of the mid 1950’s was ready for what Kelly offered stands in direct contrast to the reality of a profoundly hidebound academic and mainstream culture. — Joshs

Plainly the US wasn’t ready, and even the UK found him a minority interest. My comment was that he reflected ideas that were in the air - if you were part of the intelligentsia - but he did not feature as a thought leader in the way that “revolt” eventually played out. That is, in the hedonism and other irrational/romanticised responses that masked the US’s economic turn from a production to a consumption based system. People ended up in EST classes and multilevel marketing as the mainstream self-actualisation therapy of the yuppie 90s. :wink:

As I have said, if I am lukewarm on Kelly it is because the cognitive part of his story is already familiar and taken for granted from pragmatist philosophy, social constructionist psychology and anticipation-habit based models of neuroscience.

Then the aspect I say is being overplayed by you is how the individual point of view becomes a justification for the reheated romanticism that animates PoMo pluralism and anti-structuralism.

So you celebrate Kelly as a self-proclaimed renegade. Others might find him not particularly startling, just more of a missed opportunity in the Anglo psychological tradition that never really focused on the social construction of the individual mind.

I think the typical situation for original thinkers is that their closet competition is a tiny handful of writers. Beyond that immediate sphere of influence lies a larger circle of maybe a few thousand thinkers who are regurgitating the previous generation’s cutting edge thinking. Beyond that is a much larger circle of non-academic educated culture which represents the best of an even older generation. And beyond that is an uneducated pluraity that still identify with even more ancient ways of thinking. So as far as the wider culture influencing the work of an original thinker, I think as we move out from the small inner circle in every wider approaches , the numbers of individuals grows, and the influence becomes more and more indirect. — Joshs

Of course.

And yet also, no thinker begins outside the social circumstances that shaped them as their arena in which to begin to react as an individual.

I was talking about the impressed forces of his mechanics. Gravity as Newtonian action at a distance rather than Cartesian corpuscles is another issue in the long story of the metaphysics of physical models.

Put it this way, is there any information-talk in physics that can't be (shouldn't be) replaced perfectly well with entropy-talk? — bongo fury

They are formally complementary modes of description now. Two ways of saying the same thing.

Entropy might be composed of an ensemble of microstates, and so a system at equilibrium might appear to contain a hell of a lot of information ... all those individually distinct possible states. But then the only actual information we need about the system is the value of its macroproperties, like its temperature and pressure. In the same way that we only need values for the mean and standard deviation of a Gaussian probability distribution, we can afford to discard all the information represented in the individual microstates as they all smear into the one macro probability distribution encoded in Boltzmann's entropy equation.

Entropy is thus a model of complete randomness or disorder. And then the same equation can be inverted to arrive at the other view - the Shannon information view - where every microstate is treated conversely as a negentropic signal to be separated from the surrounding noise. The world is being modelled not as a self-organising average, a meaningless collection of accidents, but as a place where now every aspect of some particular microstate has been chosen with meaningful care.

So in entropy world, the particular gets absorbed into the general. Differences no longer make a difference worth counting. And in negentropy world, the metaphysics is inverted. Every difference now makes a difference.

Confusion then arises in threads like these because conventional notions of "information" relate to finding meaning in the world. We are semiotically seeking to distinguish signal from noise in any situation. We are discovering where we want to impose the epistemic cut in terms of everything that particularly matters (to "us") and everything that generally doesn't.

But physics is our model of reality that wants to talk about things beyond the point where they are embedded in self-centred points of view. The need to divide the world into signal and noise, meaningful and meaningless, drops out of physics' picture as it is only interested in the naked statistical mechanics - the view that can marry the metaphysical absolutes of blind chance and deterministic necessity.

So that is why physics is making this move to model the world in infodynamical terms - making use of the fact that entropy and information are inverted versions of the one fundamental statistical equation.

Used in one direction, the description of nature can treat everything as just generalised difference. Used in the other direction, the description of nature will treat everything as some matchingly particular state of affairs. Every difference now counts as a difference rather than counting as something that is a matter of indifference.

This is a neat dialectical trick that means physics has reality tied up from both directions in a framework for counting and measuring its bits or microstates.

You just need to establish the Planckscale limit on the counterfactual definiteness this infodynamic view of physics presumes. And also understand how it builds in the Gaussian bell curve version of a probability space - the world of closed systems that can equilibrate as they are statically bounded.

That assumption of a normal distribution becomes a little fraught once you realise that a scalefree or fractal distribution - the log/log distribution that is open and growing and has no actual mean - is likely the more generic story in dissipative systems. The familiar Shannon information gives way to a more general model such as Rényi entropy.

But that is a bleeding edge conversation.

The things of importance is that physicists aren't interested in the issue of meaning. They are seeking the depersonalised view of reality and so their metaphysics deliberate excludes that part of Aristotelean causality which relates to purpose and finalities. So when they speak of information - or when neuroscientists employ that physicalised version of "information" – they don't mean what most of the folk here think they ought to mean.

And then the reason why entropy and information have become fused as a new information theoretic turn in physics is that they are two ways of reading the same formula. And the formula is a step forward in moving physics from the old atomistic Newtonian paradigm to a view of reality that does a better job of rooting the descriptions in the holism of probability spaces and statistical mechanics.

Newton spoke of forces - little pushes and pulls delivered by corpuscular objects. That became generalised to quantities of energy - forceful interactions were turned into some notion of actual conserved substance that flowed. Then the pendulum swung the other way to make energy just patterns in fields. After that, we get to the entropic view of force - patterns in a probability space. And now that has been joined by the informational response that reads global pattern as individuated marks.

The analysis gets ever more remote from the original folk belief that the world is a collision of substantial entities. It becomes eventually some rationalist account of order vs disorder. A tale that is all about the abstractions of the form and purpose of Being - even though that is not something the culture of physics would want to admit.

And again, people pick up on this discomfort. Entropy and information are treated in discussions like these as the "new concrete stuff of reality", because that is what "real" has to mean to maintain a purely materialist discourse.

Panpsychism and other pathologies of reason can then set up camp on the paradoxes that result from not understanding why what is working for physics in fact works for physics.

What Kant, Hegel and Peirce had in common was their grounding of Being in divinity. — Joshs

Even great thinkers reflect their social era. Doesn't that prove my point about the social construction of even the most independently minded individuals?

Can one embrace the triadic model and discard the theology without doing violence to Peirce’s intent? — Joshs

Yep. Logic is logic.

You haven't been able to pick holes in account of that logic and so now you chose to play the man rather than the ball.

A number of your colleagues in pan semiotics are quite sympathetic to theological writers — Joshs

As I keep saying, the hard turn towards material reductionism by Newtonian science was matched by a soft-headed turn towards Romanticism and idealism in Western society. There is a generalised ache to preserve a spiritual and personal dimension in modern folk metaphysics.

So yes. It is the norm in modern society to feel there must be more to existence than just the blind and souless determinism of the "scientific world view". That is why we have cultural responses like PoMo, phenomenology, humanism, and the watered down, pantheistic, notions of the divine that are so common.

And so we may regard the disagreements as not about the facts but as due to differences in the conventions-adopted in organizing or describing the space. What, then, is the neutral fact or thing described in these different terms? — Goodman

As usual, you are quoting stuff that supports my argument. Goodman is asking for a ground in monistic facticity. And I am arguing that what grounds counterfactual definiteness is the "epistemic" process of dichotomisation. Point and line are the complementary limits of the one dialectical conception.

A point stands for the absolutely discrete, the line for the absolutely continuous. And between these two bounds on concrete possibility, we can expect to find our own reality cashed out as a measurable ground. We are always some infinitesimal degree away from arriving at the limit represented by the notion of a 0D point, and always some infinite degree away from reaching the end of the 1D line.

Kelly was opposed to rationalism, which is why he insisted his approach was not a cognitive psychology. Kelly was a renegade who attacked the core presuppositions of rationalism. — Joshs

Err. OK. So he was constructing himself as an anti-rational renegade ... yet now is recognised as just a rationalist positive psychology type responding early to the spirit of his age?

Self-actualization as a buzzword made its way into American psychology in the 1950’s due to the indirect influence of European trends such as existentialism, American pragmatism, phenomenology and Gestalt psychology. These tropes were not embraced by mainstream intellectual culture until many years later.
In the 1950’s only a handful of American psychologists and philosophers adopted them. The mainstream endorsed S-R positivism and the new discipline of cognitive science, a rationalist offshoot of 19th century idealism. — Joshs

You forgot to mention the dominance of Freudian Romanticism that was in fact the official mainstream in US psychotherapy of that era. Wasn't Kelly reacting against that?

Self-actualisation and humanist approaches took off in the US because there was already the deeply engrained notion of the US being the land of the self-made man. But by the 1950s, corporations and unions dominated the society. People were suddenly rich, secure and leisured, yet still constrained by class and traditional values. So very ready to discover themselves and construct their own personal realities.

Behaviourism was popular among those who liked the idea of mind control. It was hardly central to popular culture. Cognivitism started out naturalistic and ecological - as with Neisser - but became over-run by computer science and the metaphysics of information processing.

I'm not really buying your social history here. If you are determined to make Kelly the base of your argument against pragmatic positivism or social constructionism, that seems a poor choice.

Shannon's information theory defines information as any message that reduces uncertainty from a given set of possibilities to ONE.

Will/should skeptics be offended/pleased that all of them together amount to 0 bits? — TheMadFool

I would say this brings out the need to be able to distinguish two varieties of uncertainty.

We can be uncertain where we agree that the principle of non-contradiction, and we are simply counting the missing information. The skeptic agrees your proposition must be either true or false, 1 or 0. But they await the evidence. They see an informational gap waiting to be filled. There are known unknowns that can be quantified.

Is the cat in Schrodinger's box - the familiar quantum thought experiment - dead or alive? In the classical view, it must be one or the other. The PNC applies. The information may not be received until the lid is lifted, but there is already a fact of the matter. There is a known unknown. If you proposed the cat is by now surely dead from the poison having been released by the radioactive decay event, then the skeptic can say your claim of having reduced your uncertainty to 1 is a little premature. You could still be flat wrong in that assertion.

But then there is the uncertainty that results from the PNC not applying to some description of reality. The quantum view. It is simply logically vague as the two possibilities are in superposition until the wavefunction has been collapsed. The binary choice of 1 or 0 doesn't yet answer to any classical conception of an actual fact - a definite or crisp state of logical counterfactuality.

So you can be skeptical because the information hasn't yet been properly provided. It is person making the doubtful bivalent claim that is missing the information.

Or you can be skeptical about whether the real world is ever truly counterfactual in any situation. Behind the certainties of the bivalently encoded message - a message generated using a model of atomistic or digital information - there is always inherently a vagueness or uncertainty in regards to world as the thing in itself beyond our imposed modelling. Meaning may elude our grasp to the degree we shoehorn a proposition into a blunt binary logical frame of true or false.

Beyond the known unknowns, there are the unknowns unknowns. Beyond the quantified uncertainties, there are the unquantified uncertainties.

So absence and presence , sameness and difference , form and content are irreducible , universal requirements for any kind of world. — Joshs

It is a matter for argument whether those are the right fundamental constructs (they may or may not be). But what is truly fundamental is that dialectics is the universal logic, the universal rational process, which produces any well-formed construct.

Notice that there is nothing in this assertion to differentiate Kant’s notion of universality from Hegel’s or Nietzsche’s or Kelly’s . But when we start inquiring as to whether there are universal contents constraining the dynamics of dialectics, such as Kant’s transcendental categories subtending time, space, causation and morality, we can distinguish different kinds of universality. Like Kant , Hegel fills in the dialectic with a universal content. For Hegel, however, this content doesn’t subsist in static categorical schemes , but in the ordering logic guiding the movement of the dialectic. — Joshs

Kant fell down with his antimonies. Hegel got things a little wrong because he lacked a concept of vagueness. That is why I say Peirce worked it out best with his triadic systems perspective.

To achieve the goal of arriving at a dialectical unity of opposites, you have to find a reasonable way in which both sides of any such metaphysical symmetry breaking can actually be real - present in the one world while apparently also representing some essential contradiction.

That is why we end up understanding dichotomistic constructs as complementary limits on Being itself. The two poles of a spectrum can be part of the same reality by marking the two bounding extremes of what is possible.

Hierarchy theory then arises as the most general way of representing such a structure of Being. The simplest way to have two opposites in the same world is if they are placed as far apart as possible - as in the divide between the local and the global scales of Being. Local~global is the ur-dichotomy.

But then because synchronic structure is itself opposed to diachronic process, we also have the other ur-dichotomy of the vague~crisp - the extension to dialectical reasoning made explicit in the triadic logic of Peirce.

Peirce was always trying to connect these two dichotomies in the one world description, which is why you wind up with his super-dichotomy of tychism~synechism. The local is pure chance or pure spontaneity, so also as vague and unformed as it gets. The global is continuity and universalised habit or law, so as crisp and definite as its gets.

Thus the content that results from dialectical inquiry is that which in the end can't be done away with. Peirce makes sense to me in his reduction of existence to these two complementary ur-dichotomies - the local~global and the vague~crisp, or the dichotomies of structure and of development.

But look at the difference between the ‘flow’ experience of the intuitive , organic unfolding of a dance duet, and the hostile , conflictual exchange of a political disagreement. — Joshs

Social organisation boils down to the dialectical balancing of competition and co-operation. It needs both in balance for a society to persist as a system.

That in turn reduces to the general systems story of local~global hierarchical structure.

Competition is local differentiation and creative contest. Hostile disagreement, if you want to get rhetorical about it. Or useful individual variety, if you want to get evolutionary about it.

Co-operation is its "other" of global integration or stabilising habit. The organic unfolding of a dance duet if you want to get PoMo rhetorical about it. Or useful collective uniformity, if you want to get evolutionary about it.

So of course you will seek to frame things in a way that befits the cultural agenda of PoMo. But that is itself a highly particular viewpoint when it comes to metaphysics. My interest is in arriving instead at the most general possible one.

And as you can see, that opposes your habit of forever seeking plurality at every level of Being with the other habit of spotting the two ur-dichotomies that underlie every form of existence.

No, my perspective and that of another are not to be understood as independent, private regions. The interpersonal relation directly remakes my sense of what my `own' perspective is, as well as what I assume to be the other's integral position. — Joshs

To defend PoMo as a political set of beliefs, you must argue against the structuralism of hierarchical order. I get it.

The world must be an egalitarian network where no node carries any more weight than any other. Every interaction has the one scale - an informational symmetry rather than an informational asymmetry. You must resist any notion of the natural world as a system of nested order where some folk might actually have a more successfully generalised metaphysics than others.

Each word I use gets its sense from its categorical inclusion within a superordinate hierarchy of personal meaning. The trivial day to day events of my life get their relevance from the broader themes of my life, and the most superordinate of these involve my sense of myself as a social being. — Joshs

And this is something you learnt ... from reading some book?

My personal meanings aren’t determined by a global cultural system the way that my superordinate system determines the sense of my day to day trivial experiences. — Joshs

Have you read up on symbolic interactionism - George Herbert Mead's take that stems from the same Peircean sources? That gives a balanced account of the semiotic interaction between personal possibility and its environmental constraints.

Perhaps because Peirce himself was so notoriously awkward, he didn't cash his semiotics out at the level of social theory. :smile:

[Symbolic interactionism is a frame of reference to better understand how individuals interact with one another to create symbolic worlds, and in return, how these worlds shape individual behaviors.

https://en.wikipedia.org/wiki/Symbolic_interactionism

In a ‘community’ of five individuals in a room, I, as participant, can perceive a locus of integrity undergirding the participation of each of the others to the responsive conversation. To find common ground in a polarized political environment is not to find an intersect among combatants, a centrifugal ground of commonality, but to find as many intersects as there are participants. Each person perceives the basis of the commonality in the terms of their own construct system. — Joshs

Again, you are describing the necessity of dialectics rather than the fundamentality of the plural.

A successful network - the one with the best balance of stability and plasticity - is going to be neither over-connected nor underconnected. So neither too bound by groupthink, nor too unbound by excessive individualism.

We have formal models of these things, like tensegrity. Emergent balances that minimise the collective tensions of individuals arriving at commonality.

If indeed the fundamentalist perspective dominated the communist view in Kelly’s world, this certainly didn’t constrain Kelly’s model. — Joshs

My point was that Kelly's approach was constrained by the certitudes of 1950's US intelligentsia - the tropes of rationality and self-actualisation. He saw his impoverished Kansas farmers as needing training in how to become rational and self-actualising in a way that was a society's generally stated goal.

Now for an Islamic fundamentalist, that is a cultural goal that still might not compute. But for a systems scientist, one would say of course! If you want the right kind of self-organising whole, you must shape up the right kind of self-fitting parts.

But is it a universalizing structure? — Joshs

Of course. The dichotomy is the basis of rational analysis itself. There would be no philosophy without the dialectic.

By contrast, in Kelly's form of interlocking, any two events are just as closely related to each other as either of them is to the third. In other words, all events are inferentially, relevantly, motivationally, replicatively related to each other like an optimally enlightened construct system, which is different than saying they are just causally connected. — Joshs

Not making much sense here.

If there ain’t also differentiation then any claim of integration becomes meaningless. Things must be separated to also stand in some relation. As they say, time had to exist so not every happens all at once.

Certainly Kelly never gave up a realist-sounding language that spoke of a universe seemingly ‘out there' and which we are mirroring more and more accurately through successive approximations, but If one follows the implications of the theory itself, it seems to me what one ends up with is not a correspondence theory of truth, but rather a developmental teleology of intentionality itself directed toward endlessly increasing internal integration. — Joshs

You seem to be reading a lot into Kelly.

Notice that Kelly does not say our approximations UNCOVER what was presumed to be already there in an independently existing world. Rather, our approximations help to UNFOLD that reality. I interpret this to mean that our approximations co-create the ‘larger scheme of things’ in contingent fashion. — Joshs

Or maybe he was thinking like an organicist who also sees the natural world as an unfolding development rather than a grounded construction. Maybe it was that he was trying to articulate? Reality as a series of ever more definite symmetry breakings.

Does the cultural context constrain the theory like a frame that limits the range of variations that can occur within it, or does each individual participant redefine the boundaries of the frame in some measure? — Joshs

As usual, you are advancing a false dichotomy because you haven’t got how this goes. The global social constraints are meant to shape the individual’s psychological development in some time-proven useful way. But as I’ve said, the same system wants to be able to learn and adapt, and so a tolerance for local variety is also part of the deal. If every individual interprets cultural norms according to their own local contingencies, then that feeds back cybernetically to ensure the collective social order can change its own global settings. The whole system can adjust.

So culture makes frames and individuals can promote change. Sounds like the usual way evolution gets done to me.

There were communists , libertarians and John Birchers, Christian Fundamentalists and atheists, Freudians and Skinnerians, — Joshs

But perhaps not one communist for every one fundamentalist. Care to guess at a realistic ratio?

But is any major thinker just a product of their time or does a Descartes, Kant , Hegel extend the frame and move slightly beyond their ‘time’? — Joshs

Again, why would I be arguing that folk are prescriptively products of their upbringings when I was quite explicit that global constraints are meant to shape the local productive freedoms of a system?

Even today , 70 years later , one can hardly claim that Kelly’s perspective characterizes the mainstream intellectual climate there yet. — Joshs

So much for the diversity you claimed for Kansas folk just a sentence or so earlier.

What we possess, or what we have achieved so far, are approximations of the truth, not fragments of it. Hopefully we are getting closer, in some sort of asymptotic progression, — Kelly

This is Peirce’s pragmatic definition of truth as the limit of rational inquiry by a community of thinkers, by the way. Just saying. :grin:

What about Kelly’s constructive alternativism? How would you state the mindless universalism and polarity he settles on? Elevating the personally psychological and its dichotomous processes to pre-eminent status? — Joshs

Kelly gets the dichotomous nature of constructs. His repertory grid technique is designed to find - and even construct - robust dialectical structure in some Kansas farmer’s habits of social reaction.

And how should we then read his efforts to impose a therapy that indeed imposes a universalising rational structure on the perhaps idiosyncratic and fairly contingent social learning of that farmer?

Is it the farmer that does all his or her own self-actualising? Are the constructs truly personal creations that are merely being excavated and brought finally to light?

Or are they vaguely organised thoughts being constrained within a cultural context - such as the US circa 1950 - that prized both rationality and individuality, and so made it natural to frame its therapeutic interventions in that fashion?

And then you come along with your phenomenology, affect, and PoMo pluralism, and somehow shoehorn your reading of Kelly into that.

I wonder why the circa 2020 Kansas farmer might seem such a different creature if Kelly were still around? Did something happen to the dream of universalising rationally-structured individuality in the decades of mindless culture wars inbetween?

Who is it who is claiming there is a trans-communal and trans-species moral
system? — Joshs

Do you believe in the UN Universal Declaration of Human Rights? That kind of thing. [Oh, and I meant to write pan-species of course.]

In Kelly's approach, even when someone lives in a culture which is tightly conformist, one neither passively absorbs, nor jointly negotiates the normative practices of that culture, but validates one's own construction of the world using the resources of that culture. — Joshs

My constraints-based systems approach also stresses the personal creativity that is inherent here - especially to the degree the culture has developed a rhetoric of self-actualisation … because it means to shape up that kind of personal creativity.

Again, we are biological selves - that kind of social creature - before we are modern cultural selves - that other kind of creature. So there is alway going to be a deeper evolved level of self-social group action that a culturally-constructed system of self-group interaction is going to have to contend with.

One can see how the ‘tremendous variety of ways' that participants are capable of interpreting the ‘same' cultural milieu makes any attempt to apply a group -centered account of social understanding pointless. — Joshs

Seems odd there can both be a cultural milieu and yet deny its existence in the same sentence.

But maybe that’s only a paradox for a view of social systems that doesn’t get the notion of how global constraints are also the source of local freedoms.

If we are all limited to using the same language, then we are also all freed to be definitely (and not vaguely or tentatively) saying different things. Unity and plurality go together if you have the right understanding of systematic organisation - an organismic one rather than a mechanical one.

No one has yet proved himself wise enough to propound a universal system of constructs. We can safely assume that it will be a long time before a satisfactorily unified system will be proposed. For the time being we shall have to content ourselves with a series of miniature systems, each with its own realm or limited range of convenience. As long as we continue to use such a disjointed combination of miniature systems we shall have to be careful to apply each system abstractly rather than concretively. For example, instead of saying that a certain event is a ‘psychological event and therefore not a physiological event', we must be careful to recognize that any event may be viewed either in its psychological or in its physiological aspects. — Kelly

This sounds fine. But why doesn’t Kelly talk about the duality of physiological and cultural events?

Psychology is where these two sources of self-world construction intersect. But let’s carve the problem at its actual naturalistic joints.

How do you reconcile “There is no ultimate constraining unity at the end of the line” with “ We all have to live not by local acceptable custom but by the iron law of what is universally correct.” — Joshs

The systems view - as Salthe makes clear - is based on the structuralism of nested hierarchies. So a local-global balance is something struck in fractal fashion over all possible scales of organisation.

So there is no iron law than floats abstractly above the system. That is an externalist and mechanical trope. Instead, an organism is a unity of its habits. It is aligned to achieve its end over all scales of its being.

What is deemed local acceptable custom will be so deemed to the degree that it institutionalises what is globally acceptable custom. And being constraints based, this doesn’t demand absolute homogeneity. Indeed, creative variety is necessary. Every organism must have variety to keep evolving and adapting to a world that is also forever changing.

An organism must also have its aligned structure of habits as well so as to even be a persistent, because adequately adapted, organism.

Again, an organism is a balance of plasticity and stability. And that means also that it is a fruitful balance of unity and plurality, sameness and difference, integration and differentiation - and all the other ways of saying the same thing.

So the organic view starts from that as its dichotomous ground. Which is helpful as it is then already equipped to ask more useful questions about what some particular balancing of the dynamic ought to look like. You could have a political discussion, for example, where both poles of the spectrum are taken for granted and the debate turns to how much liberty there should usefully be in your conservatism, and how much conservativism there should usefully be in your liberalism.

That is, the kind of debate that exists in countries happy to label themselves social democracies.

But don’t you think one could lay out a spectrum of positions within ‘structuralism’ and pomo such that it becomes difficult to discern the actual
boundary between them? — Joshs

Sure. But what if structuralism is the position that is built on the dichotomous trick that produces such connecting spectrums and PoMo treats dichotomies as monistic and politicised choices?

Why do so many folk gravitate to Wittgenstein? Is it not because he represents the “clarity” of the division between the univocal and the pluralist factions? First he was all about rationalist certainty, then he was all about language games. His career path embodies the schism. And his fans applaud him for landing eventually on the “right side of history”.

Part of what’s throwing me here is that , while I do make use a notion of dialectic , it is closer to George Kelly’s concept of the construct as dichotomous. — Joshs

Yep. Kelly starts off being quite Peircean, but then drags things off in the direction of pluralism.

So we see his good start in grounding his psychology in habits of prediction - a modelling epistemology that roots "mind" or "self" in a pragmatic and embodied metaphysics and so begins in the right place, as opposed to the wrong place of Cartesian representationalism.

His fundamental postulate says this: "A person's processes are psychologically channelized by the ways in which he anticipates events."

This is the central movement in the scientific process: from hypothesis to experiment or observation, i.e. from anticipation to experience and behavior.

And Kelly gets the dichotomous nature of constructing constructs - the generalities that ground the ability to then particularise in terms of individuated balances on some spectrum that lies between "two poles of being".

The dichotomy corollary

"A person's construction system is composed of a finite number of dichotomous constructs."

We store our experience in the form of constructs, which he also referred to as "useful concepts," "convenient fictions," and "transparent templates." You "place" these "templates" on the world, and they guide your perceptions and behaviors.

But then he starts to veer off into the dogma of pluralism....

He often calls them personal constructs, emphasizing the fact that they are yours and yours alone, unique to you and no-one else. A construct is not some label or pigeon-hole or dimension I, as a psychologist, lay on you, the "ordinary" person. It is a small bit of how you see the world.

The young child doesn't care if you are fat or thin, black or white, rich or poor, Jew or Gentile; Only when the people around him or her convey their prejudices, does the child begin to notice these things.

Yet if we are talking about the mind and its model of physical reality, then the dichotomies are objectively real in that reality self-organises via its fundamental symmetry breakings. The Universe is not pluralistic but unified as a system.

So it is only at the socially constructed end of our reality modelling - the end where the opposition of the personal and the public is being manufactured, the romanticised dichotomy of individuated self and collectivising society – that these kinds of personal constructs, or localised prejudices, start to become a thing.

And indeed, it is only as we take a universalised view of the human condition - one that sees rich and poor, Jew and Gentile, black and white, toned or lard-arse, as all members of the same tribe – that the differencing also makes sense.

Our chore becomes the one of placing ourselves as free individuals within some vast space of seven billion people all meant to live by the same social code. Any local diversity or plurality is a freedom gained by accepting some even more trans-communal and pan-species moral system and Platonic-strength abstraction.

We all have to live not by local acceptable custom but by the iron law of what is universally correct - which of course breaks into its dichotomies as its must. If there is a coherent leftish position, it is automatic that there is a rightish position that is just as loud and proud in its cultural demands.

Anyway, getting back to Kelly...

The individuality corollary

"Persons differ from each other in their construction of events."

Since everyone has different experiences, everyone's construction of reality is different. Remember, he calls his theory the theory of personal constructs. Kelly does not approve of classification systems, personality types, or personality tests. His own famous "rep test," as you will see, is not a test in the traditional sense at all.

The commonality corollary

"To the extent that one person employs a construction of experience which is similar to that employed by another, his psychological processes are similar to the other person."

Just because we are all different doesn't mean we can't be similar. If our construction system -- our understanding of reality -- is similar, so will be our experiences, our behaviors, and our feelings. For example, if we share the same culture, we'll see things in a similar way, and the closer we are, the more similar we'll be.

In fact, Kelly says that we spend a great deal of our time seeking validation from other people. A man sitting himself down at the local bar and sighing "women!" does so with the expectation that his neighbor at the bar will respond with the support of his world view he is at that moment desperately in need of: "Yeah, women! You can't live with 'em and you can't live without 'em." The same scenario applies, with appropriate alterations, to women. And similar scenarios apply as well to kindergarten children, adolescent gangs, the klan, political parties, scientific conferences, and so on. We look for support from those who are similar to ourselves. Only they can know how we truly feel!

So good. Both the personal and the public are being recognised. But bad. It isn't being framed as a dichotomy of localised construction and globalised constraint.

It is only about the bottom-up construction which thus roots things in the individual and leaves the communal as some kind of collection of accidental choices rather than a larger universalising view that has evolved to provide a generalised constraining hand over local acts of individuation.

We are veering off the good old structuralist road and heading into the familiar post structuralist ditch.

Feelings

The theory so far presented may sound very cognitive, with all its emphasis on constructs and constructions, and many people have said so as their primary criticism of Kelly's theory. In fact, Kelly disliked being called a cognitive theorist. He felt that his "professional constructs" included the more traditional ideas of perception, behavior, and emotion, as well as cognition. So to say he doesn't talk about emotions, for example, is to miss the point altogether.

What you and I would call emotions (or affect, or feelings) Kelly called constructs of transition, because they refer to the experiences we have when we move from one way of looking at the world or ourselves to another.

This ain't too bad a start to the degree it treats affect as a particular class of embodied action - the action of reorienting the mind and body as surprise produces the necessity of revising your expectations.

That is what I was saying about the orienting reflex literature. No one ever realises how much of the brain is devoted to the complexities of knowing how to be looking in the right place most of the time. A large chunk of motor cortex is devoted to getting our senses and physiological state aligned in a forward looking fashion.

Embodied action ain't just about motor plans that might manipulate the physical world in some self-interested way. It is just as much about shifting this "experiencing and deciding self" to a new and better placed set of receptive and affective co-ordinates.

Psychopathology and Therapy

This brings us nicely to Kelly's definition of a psychological disorder: "Any personal construction which is used repeatedly in spite of consistent invalidation." The behaviors and thoughts of neurosis, depression, paranoia, schizophrenia, etc., are all examples. So are patterns of violence, bigotry, criminality, greed, addiction, and so on. The person can no longer anticipate well, yet can't seem to learn new ways of relating to the world. He or she is loaded with anxiety and hostility, is unhappy and is making everyone else unhappy, too.

If a person's problem is poor construction, then the solution should be reconstruction, a term Kelly was tempted to use for his style of therapy. Psychotherapy involves getting the client to reconstrue, to see things in a different way, from a new perspective, one that allows the choices that lead to elaboration.

Here we see the problem of failing to distinguish between the biological and cultural sources of semiosis that shape the individual person. It is bad enough to reduce social constructs to personal acts of construction. It is really bad to omit the biological basis of a person's world modelling.

Of course, as pragmatics, PCT can do some good as a therapeutic practice. But I would prefer therapy that is more squarely based on good psychological theory - that is one that is rooted in a social psychology model.

Modern positive psychology is broadly such an approach. It helps people realise the degree which they have habitualised family, community or general cultural imperatives. They have learnt to make automatic at an uncritical age various ways of thinking that might not be terribly useful in terms of their own lives, especially as humanity becomes increasingly mobile and increasingly rapid in its collective changes.

By this he means it is a way in which two events are alike and different from a third. Your use of dialectic seems closer to that of Hegel. — Joshs

Well yeah. Have you seen the actual mathematical definition of a dichotomy - the one I have cited so many times? Two poles of being that are mutually exclusive and jointly exhaustive?

But one indeed might have to triangulate to start to divide reality into a pair of complementary poles. The certainty of the dialectic might well have to start with the tentativeness of exploring a relation in which the similarity of two things can now start to oppose a mutual differencing from some third.

Or as Peirce said, make that move from the Secondness of bare reaction to the Thirdness of holistic relation.

The dichotomozation a construct effects isnt the kind of othering or antithesis we see in Hegel’s dialectic. It is more along the lines of a variation or modification. — Joshs

Oh quick. Before our start gets us to the "wrong" destination, let's jump our escape hatch and return to the comfort of PoMo pluralism.

There is no ultimate constraining unity at the end of the line. There is just all us little chirping personalised differences - small, accidental, and localised reactions that constitute a Secondness that doesn't want to venture any further into the thickets of grand univocal metaphysics.

One can always see pomo in opposition to what came before it, but a closer look should reveal an intricate development within pomo that bridges what came before such that the appearance of dialectical conflict and othering is replaced by something more on the order of a continuum of historical change. — Joshs

I'm sure the post-structuralists had no violent intentions when it came to smashing structuralism. It was just a helpful conversation to help the old guard come to see the error of its ways.

But anyway, as usual, as always, as a habit you can't avoid, you talk right past my dialectical framing of my dialectical position.

A dichotomy is about the conflict that produces the complementary. Society is about the local competition or individuated freedom made possible by the co-operation or global constraint that could give this freedom is meaningful shape and constructive role.

So for me, unity and pluralism go together as the obvious two sides of the one triadic coin. Hierarchy theory exists to spell that out as a lesson in structuralism making good on its promise.

You are creating excuses for PoMo. But they don't wash.

Of course - as getting into the detail of Kelly illustrates - any individual writer of any note always grasps the systems perspective to some degree. They have to, as that is simply the way reality is.

What I am complaining about is the pervasive tendencies that result as social camps spring up around opposing poles of the dichotomies that thus arise from any critical analysis. The mindless pluralism that seeks out the best available examples to find the mindless universalising that makes its own mindless polarity the "definitely right one".

The difference between the poles of your dialectic ( or the in-itself of firstness) and the poles of my interbled unity is that your starting point is inert, dead, static, and only is brought to life by adding a relation to it in a secondary move. Saying it’s vague, fuzzy, dances around or fluctuates doesn’t avoid the problem that it is still treated as an intrinsic thing. — Joshs

You are not getting it, just continuing to impose your own frame of reference on a discussion of Peirce and a triadic systems logic.

However, at the level of the psychological and the cultural , your account has a lot of competition from enactivist, poststructuralist , hermeneutic, social constructionist , phenomenological and deconstructive alternatives which all view language as self-referential rather than pointed toward an ‘out there’. — Joshs

You continue to fail to get it. I've repeatedly said self and world are co-constructed through the semiotic relation that is a code mechanism like language. The use of language brings out those two things as opposed poles of "being".

The danger of that is the social construction of self and world as each other's Hegelian "other" can then so easily be collapsed into the doubled monism of Cartesian dualism. World and self become two varieties of substance - the error panpsychics then compound by making them two properties of one ultimate material.

So yes, there may be "competition". But it is muddle-headed to the degree it mires itself in dualism and monism.

Pluralism is no problem for the triadic view, just as unity is also not a problem. The dialectic provides the unity that reduces one-ness and many-ness to being two complementary limits on the possibilities of existence. You can approach either pole asymptotically, but never - in ying-yang fashion - arrive at one or other limit, and thus exceed the world of the boundedly possible.

So you are arguing PoMo's case for the plural, the arbitrary, the individual - the case it must make to distinguish itself from its natural "other". That other is identified as a metaphysics which instead gravitates to the other pole that is univocal or in other ways prescriptive, constraining, hierarchical, etc, etc.

I get it. This is a cultural war that became entrenched after the unifying forces of the scientific enlightenment triggered their own natural dialectical response in a Romanticism that sought its identity in being rationality's "other".

So PoMo is a historical inevitability. As Scientism grows as one politicised pole of cultural being, its opposite pole must also become a camp of thought to right the balance - right the balance in terms of being able to measure a distance from each other, or preferably a chasm, that leaves two sides which are "poles apart". :lol:

It is amusing to see this playing out even in the debate over how language is used to socially construct the semiotic sense of being a self in its world - Vygotsky batting for Hegelian/Enlightenment unity and Bakhtin for PoMo pluralism....

https://www.researchgate.net/publication/254081081_Contrasting_Vygotsky%27s_and_Bakhtin%27s_approaches_to_consciousness

The brand of realism that you and Peirce subscribe to would not be possible without nailing down an inert( inert not because it isn’t vague or fluctuating , but because it is intrinsic before it is relational ) if temporary, ground. — Joshs

You still don't get it. Or rather, you must pretend that every dialectical claim is a dualism yearning to become a monism in disguise.

Your hope is to lift the veil of opaque triadic texts and find the same old reductionist machinery that places you back in familiar territory. You can take a firm stand with your comrades by standing squarely on PoMo ground and start throwing the conventionalised insults at your traditional "other".

Again, if you understand logic, you should get what it might mean that vagueness is logically defined as that to which the PNC fails to apply. It is a construct that can ground the resulting dialectical division that is the first intelligible moment of when the PNC might begin to apply.

But "grounds" are themselves crisp and not vague. So vagueness is also "other" to the notion of grounding. And that means we can only even talk about it from the vantage point of some dialectic framing - like vague~crisp indeed, or the PNC's failure vs the PNC's success - that provides a measurable degree of othering.

It gets tricky in terms of the mental gymnastics. But it is what it is. It sorts folk out pretty fast.

I want to focus on the language you are using here. I know it is tentative, but let me start with infinite. Infinity pertains to an already established category of meaning, the counting of instances of a theme. What ever it is that has infinite instances of it maintains its sense throughout the counting. It is an infinitely counting of a ‘this’ thing or this phenomenon or this vagueness or this fluctuation. So what is the category here that is infinite? — Joshs

You are asking me to repeat whole tracts of Peirce or Rosen who cover these issues of mathematical conception. It is a well traversed terrain.

But I will just point out that infinity is one limit on unbounded counting, and the infinitesimal is its “other”. And it is a reciprocal or dichotomous definition, 1/ infinity = infinitesimal/1. And vice versa.

So counting seems to make sense just as it seems to make sense that a line is a infinite series of points, and every one of those points can still be infinitely divided as just very small intervals.

In other words, it doesn’t bloody make sense as Peirce and Rosen will tell you. And it directly leads to the need for our models of reality to presume their epistemic cuts.

What about the term ‘fluctuation’ . In order to fluctuate , mustn’t something change over time? So this wouldn’t be a singular thing we are talking about but already a complexity , a changing process. Would a fluctuating then not presuppose a multiplicity of some sort , now behaving this way, now that way? — Joshs

Again you are simply applying a reductionist habit of thought and finding paradox in a triadic dialectics. Why should I have to go through the same conceptual loop every time?

If you didn’t follow the Salthean explanation in terms of cogent moments, what more can I say?

Shouldn’t the answer be ‘both’? It seems to me Peirce is presupposing two states ……( — Joshs

One more time you want to abandon the internalism that you claim as your thing. Everything must have some monistic ground rather than co-arise as a dialectical process.

. As you know, a color only appears as what it is relative to the background we see it against. — Joshs

As I know, hues are experienced via opponent channel processing. So red is a lack of greenness, blue is a lack of yellowness - to give the crude starting story.

This notion of interbleeding is not one that is part of the language of physical science , nor is it part of biosemiotics as far as I can tell. It also is not present in Descartes. Kant , Hegel or the other Romantics. — Joshs

I see that the mention of Mach Bands went whoosh right over your head then. Gestalt psychology says interbleeding is the opposite of what brains do in imposing intelligible structure on experience. Psychophysics cashes out von Uexküll’s story on phenomenology as a semiotic Umwelt.