I would say that I've made a considerable effort the past several years to understand your point of view. — fishfry

Yes, I've apprehend this, and I respect it. I know that's why you keep on engaging me. it's not easy to understand unorthodox and unconventional ways of thinking like mine though, so I've seen your frustration. But I do appreciate the effort. I've see the same effort to understand from jgill. I don't think TonesInDeepFreeze quite has that attitude though, and Luke just seems to be always looking for the easiest ways (mostly fallacious) of making me appear to be wrong, no matter what I say.

When you pooh-poohed the 13-digit accuracy of the measurement of the magnetic moment of the electron, you indicated a dismissal of all experimental science. — fishfry

Let me tell you something. The magnetic moment of an electron is a defining feature of how magnetism effects a massive object. Therefore it is not measured it is a stipulation based in specific assumptions such as a circular orbit. But if the electron's orbit is really not circular, then the stipulated number is incorrect.

Luke just seems to be always looking for the easiest ways (mostly fallacious) of making me appear to be wrong, no matter what I say. — Metaphysician Undercover

You don't need my help with that.

You asserted that natural numbers are not countable because they are imaginary:

There is really no reason to attempt to count the natural numbers, when we know that this is impossible because they are infinite. And numbers are not even countable objects in the first place, they are imaginary, so such a count, counting imaginary things, is a false count. Therefore natural numbers ought not be thought of as countable. — Metaphysician Undercover

You then stated that "we can only count representations of the imaginary things, which exist as symbols."

I pointed out that imaginary things have no existence other than their symbols or representations, so counting the symbols or representations is, in fact, counting the imaginary things. For example, counting imaginary sheep is really counting.

You tried arguing that imaginary things cannot exist only as their symbols or representations, and implied that they must have some real existence despite being imaginary. That is, you implied that all representations or symbols (including those of imaginary things) must necessarily represent or symbolise something real.

You then claimed that imaginary things are "a self-contradicting set of ideas". (Perhaps others will appreciate the irony that ideas are also imaginary things.) Presumably this claim was based on your implied, unfounded stipulation that all representations or symbols must necessarily represent or symbolise something real. So it's no wonder that you failed to tell us why imaginary things are self-contradicting ideas.

Yes, I've apprehend this, and I respect it. I know that's why you keep on engaging me. it's not easy to understand unorthodox and unconventional ways of thinking like mine though, so I've seen your frustration. But I do appreciate the effort. I've see the same effort to understand from jgill. I don't think TonesInDeepFreeze quite has that attitude though, and Luke just seems to be always looking for the easiest ways (mostly fallacious) of making me appear to be wrong, no matter what I say. — Metaphysician Undercover

After a little lighthearted back-and-forth (/s) over on the Israel/Palestine thread it's nice to return here to the things that really matter!

I have taken your point a long time ago that I can't actually \give a logically coherent definition of a mathematical object that doesn't depend on the contingent opinions of mathematicians. But I can't agree with your apparent extrapolation from that to an apparent rejection of all abstract math.

Let me tell you something. The magnetic moment of an electron is a defining feature of how magnetism effects a massive object. Therefore it is not measured it is a stipulation based in specific assumptions such as a circular orbit. But if the electron's orbit is really not circular, then the stipulated number is incorrect. — Metaphysician Undercover

I'm not enough of a physicist to comment. My point was only that you seemed to reject QM for some reason. I noted that you can't dismiss it so trivially, since QM has a theory -- admittedly fictional in some sense -- but that nevertheless corresponds with actual physical experiment to 13 decimal places. That's impressive, and one has to account for the way in which a fictional story about electrons can so accurately correspond to reality. Of course all science consists of historically contingent approximations. But lately some of the approximations are getting really good. Your dismissal seems excessive.

FWIW I don't think anyone thinks the orbits are circular anymore. They're quantum fields, sort of everywhere at once, and in any particular place only with a calculable probability. Or even worse, we can calculate the probability of where we'll find it if we look. Where it "really" is, is a matter of metaphysics. The question lies outside of science.

Now I agree with you (if this is what you are saying) that this makes the whole enterprise metaphysically suspect in some sense. But you still have to account for the amazing agreement of theory with experiment. We might almost talk about the unreasonable effectiveness of physics in the physical sciences!

You might think, that "the meaning is always clear from context", but if you go back and reread TIDF's discussion of counting a quantity, you'll see the equivocation with order.

I'm taking this from the end of your post and addressing it first to get it out of the way. As I mentioned, I didn't read any posts in this thread that didn't mention my handle. I only responded to one single sentence of yours to the effect that numbers are about quantity. I simply pointed out that there is another completely distinct use of numbers, namely order. Anything else going on in this thread I have no comment on.

All I saw in you demonstration was a spatial ordering of symbols. I really do not see how to derive a purely abstract order from this. If you truly think that there is some type of order which is intelligible without any spatial or temporal reference, you need to do a better job demonstrating and explaining it.

I assure you, I am very interested to see this demonstration, because I've been looking for such a thing for a long time, because it would justify a pure form of "a priori". Of course, I'll be very harsh in my criticism because I used to believe in the pure a priori years ago, but when such a believe could not ever be justified I've since changed my mind. To persuade me back, would require what I would apprehend your demonstration as a faultless proof. — Metaphysician Undercover

I may not be fully aware of the philosophical context of your use of "a priori." Do you mean mathematical abstraction? Because I am talking about, and you seem to be objecting to, the essentially abstract nature of math. The farmer has five cows but the mathematician only cares about the five. The referent of the quantity or order is unimportant. If you don't believe in abstraction at all (a theme of yours) then there's no hope. In elementary physics problems a vector has a length of 3 meters; but the exact same problem in calculus class presents the length as 3. There are no units in math other than with reference to the arbitrarily stipulated unit of 1. There aren't grams and meters and seconds. There's no time or space, just abstract numbers. I don't know how to say it better than that, and it's frustrating to me that you either pretend to not believe in mathematical abstraction, or really don't.

Looking ahead a bit I will try to explain abstract order after I respond to your other remarks.

There is an issue though, that I'll warn you of. Any such demonstration which you can make, will be an empirical demonstration, using symbols to represent the abstract. — Metaphysician Undercover

You can't get civilization off the ground without abstract symbolic reasoning, from language to math. Even music has a notation. But the notation is not the music, I hope you'll agree. Likewise the notational explanation of ordinals won't be the ordinals. I can show you the symbols but you have to hear the music on your own. That's the tricky bit, right?

This is a good point so I'll repeat it. You would not confuse music with its notation; so I hope you'll indulge my mathematical notation in the service of communicating abstract ideas. The ideas aren't the notation. We agree on that. You seem to want to deny the ideas themselves simply because they're abstract. That's the part of your viewpoint I don't understand.

So the onus will be on you, — Metaphysician Undercover

To explain to you the theory of ordinal numbers? I don't know if I can do that but I'll give it a shot.

to demonstrate how the proposed "purely abstract order" could exist without the use of the empirical symbols, — Metaphysician Undercover

No. That can't be right. You are correct that I believe that there is a notion of purely abstract order; and that I'm constrained to talk about it using symbols that are not the actual things being talked about. But you can't reject my presentation because of that. You can't deny the quest for justice just because it's an abstract idea that is not literally present in the string "justice." If you reject all human abstractions, there's no point in my starting, because you'll just say, "Oh that's only symbolic representation of things that don't exist." I can't overcome that level of nihiism.

or else to show that the empirical symbols could exist in some sort of order which is grounded or understood neither through temporal nor spatial ideas. — Metaphysician Undercover

Well, as it happens, Cantor discovered ordinal numbers when he was studying the zeros of Fourier's trigonometric series; which were an abstract mathematical model of heat distribution. That is, one can make the case that if you heat up one end of an iron bar under lab conditions, and carefully measure how the heat travels to the rest of the bar; you will inevitably discover the transfinite ordinals. There is physics behind abstract order theory. Nevertheless, the theory stands on its own as an expression of the notion of purely abstract order.

I'll tell you something else though, I have opted for a sort of compromise to this problem of justifying the pure a priori, by concluding that time itself is non-empirical, thus justifying the temporal order of first, second, third, etc., as purely a priori. — Metaphysician Undercover

I see your annoyance. I want to talk about first, second, third, but I don't want to relate them to first base, second base, or third base. I want to regard ordinals as pure ideas that can be arranged in purely abstract order. If you utterly reject that then we're done. All I can do is try to explain how mathematicians view the subject of abstract order. I can't convince you that such a thing exists. But I don't need to. I can fall back on formalism and say that even if it doesn't exist, it's a fun mental pastime, like chess. There's no physical referent for chess but it's fun and educational and some practitioners take it very seriously indeed. But it's not real. I'm sure I've made this analogy before.

However, this requires that I divorce myself from the conventional idea of time which sees time as derived from spatial change. Instead, we need to see time as required, necessary for spatial change, and this places the passing of time as prior to all spatial existence. — Metaphysician Undercover

There is no need for time or space in math. I can't talk or argue or logic you out of your disbelief in human abstraction.

This is why I said what I did about modern physics, this position is completely incompatible with the representation of time employed in physics. In conceiving of time in this way we have the means for a sort of compromised pure a priori order. It is compromised because it divides "experience" into two parts, associated with the internal and external intuitions. The internal being the intuition of time, must be separated from "experience" to maintain the status of "a priori", free from experience, for the temporal order. So it's a compromised pure a priori. — Metaphysician Undercover

And yet they get 13 decimal places of agreement between theory and experiment. That has to count for something. It's all we've got. It's helped us to crawl out of caves and build all this. For whatever that's worth.

I didn't deny the distinction between quantity and order, I emphasized it to accuse Tones of equivocation between the two in his representation of a count as bijection. — Metaphysician Undercover

I can't comment on your conversations in this thread that I didn't read. But as a technical matter, in cardinality theory we care about bijections. In order theory we care about order-preserving bijections.

That is exactly why I attack the principles of mathematics as faulty. There are empirical principles based in the law of identity, by which a physical, and sensible object is designated as an individual unit, a distinct particular, which can be counted as one discrete entity. There are no such principles for imaginary things. — Metaphysician Undercover

Doesn't Captain Kirk = Captain Kirk? Look, we're never going to get to ordinals at this rate. I don't know what you mean that the law of identity doesn't apply to fictional entities but there's a whole philosophy of fictional entities that I don't know much about.

Imaginary things have vague and fuzzy boundaries as evidenced from the sorites paradox. so the fact that "there is no mathematical difference between counting abstract or imaginary objects...and counting rocks", is evidence of faulty mathematics. — Metaphysician Undercover

You just phrase things like that to annoy me. How can you utterly deny human abstractions? Language is an abstraction. Law, property, traffic lights are abstractions. So is math.

As I said, all you've given me is a representation of a spatial ordering of symbols. If you are presenting me with something more than this you'll have to provide me with a better demonstration. — Metaphysician Undercover

This thread's already long. Do you want me to talk about ordinals or not?

I go both ways on this. Of space and time, one is continuous, the other discrete. But this is another reason why I think physics has a faulty representation of space and time, they tend to class the two together, as both either one or the other. — Metaphysician Undercover

Ok, you reject math, you reject physics. And you miss the distinction between physics and metaphysics, between a mathematical model and the thing being modeled. Whatever. Let me talk about ordinals.

Ordinals as abstract order types
========================

I'll keep this relatively brief since the rest of the post is long. I hope we can talk about ordinal numbers and not have any more endless disagreements about human abstraction. Our capacity for abstraction is one of the foundations of civilization, along with the opposable thumb. It's pointless to argue about it.

Ok first finite sets. You have a class full of school kids. You line them up by height. Or you line them up alphabetically by last name. Two distinct ways of ordering the same set. One cardinality but two distinct orders.

However, you will observe that these two distinct orderings nevertheless have the same order type. By that I mean that there is an order-preserving bijection between the set of kids in height order, and the set of kids in alpha order. You just match the first to the first, the second to the second, and so forth.

It's not hard to believe, and not hard to prove, that any two distinct orderings of a finite set have the same order type; in other words, that there is an order-preserving bijection. or order isomorphism, between the two orders. So orders on finite sets aren't very interesting.

So now, infinite sets. In fact only one infinite set is of interest to us at the moment, the natural numbers $\mathbb N = \{0, 1, 2, 3, 4, \dots \}$.

I hope you will grant me the abstract existence of this set, else there's nothing to talk about.

And I hope you won't be so tedious as to complain, "Well those dots are bullshit and they don't really stand for anything or mean anything blah blah blah." I pretty much agree with you, literally. The notation is only suggestive of a deeper abstract truth, that of the idea of an endless progression of things, one after the next, with no end, such that each thing has an immediate successor. Again if you want to stand on a soapbox and deny that, there's no point in this conversation. You have to at some level believe -- or at least accept, for purposes of playing the game -- the reality of such an endless progression. $\mathbb N$ is not the symbol or the list in brackets with the mysterious dots at the end. That's only a notation for the music. I want you to imagine the music, and form an association in your mind between the symbols, and the deeper abstract idea they represent. Surely you must be able to do this, after all you do it just fine using the English language. It's not really any different. Meaningless symbols that stand for abstract ideas. You do it every day with letters and words. It's no different in math.

Now the set of natural numbers $\mathbb N = \{0, 1, 2, 3, 4, \dots \}$ has no inherent order. You may recall that sets have no order. The set {a,b,c} and the set {b,c,a} are the exact same set. This is in fact the axiom of extensionality in set theory. It says that one of the rules of the game of set theory is that two sets are the same if and only if they have the exact same elements.

So given this set $\mathbb N$, we would like to put an order on it. What is an order? Well again, we play a symbolic game. We say that an order is a binary relation on a set that's reflexive, antisymmetric, and transitive. These terms are defined in the Wiki article I linked but they're not important. What is important is that they characterize the binary relation that we usually call $\leq$, the "less than or equal" relationship.

In the present case we also require that the order be total, in the sense that given two elements $x$ and $y$, either $x \leq$ or $y \leq x$.

And finally for convenience in this context, we prefer to work with the strict order $\lt$, which works like "less than or equal" but we disallow the equal; that is, $n \lt n$ is disallowed. Again this is all common sense that you already know, the details aren't important.details aren't important.

What IS important is that we have defined order without regard to any external meaning. It's all a formal symbolic game.

Then, we can formally define the symbols 0, 1, 2, 3, ... according to von Neumann's clever idea such that $0 \in 1 \in 2 \in 3 \in \dots$

Having done this, we now have a formal definition of each natural number within the rules of set theory; and then we can make the definition: $n \lt m$ just in case $n \in m$.

The point of all this is that we can define the '<' relation without regard to quantity and without regard to time or space or anything physical or meaningful. It's just an arbitrary symbol in the formal game of set theory; in principle no different to saying how the knight moves in chess.

Having done that, we have defined what's known as the usual order on $\mathbb N$. It's the order you learned in grade school, the one everyone knows. But the point is that I have defined '<' in such a way that this order relation means nothing at all other than the formal relation of set membership; which in set theory actually has no definition at all. $\in$ is an undefined symbol, just as point and line are in Euclidean geometry.

Having now stripped the usual order of any meaning, I'm free to define alternate orders like $\prec$ that I defined earlier; which is the same order as $\lt$ except that $n \prec 3$ for all $n \neq 3$.

This is clearly an alternate order on $\mathbb N$, just like lining the kids up by height versus by alpha last name. But in this case, these two orders represent distinct order types. There is in fact no conceivable way to create an order-isomorphism between these two ordered sets $(\mathbb N, \lt)$ and $(\mathbb N, \prec)$.

We can see this because $(\mathbb N, \lt)$ has no largest element, and and $(\mathbb N, \prec)$ does: namely, 3.

Now what I have outlined is the mathematical point of view in which:

* Order is an entirely arbitrary and meaningless binary relation on a set;

* That there are multiple possible orders on a given set; and that

* In the case of infinite sets, there can be distinct orders that are also distinct order types; that is, there are distinct orders that can not be put into order-isomorphism with each other.

This is the foundation of the idea of ordinal numbers, which are just order types of sets. And in passing, I hope I have made the point that while you object to the meaninglessness of math; on the contrary, it's the very meaninglessness of math that is essential! We have stripped all notion of external meaning from the order relation; in order to be able to investigate the properties of order without regard to the things that may be ordered.

What you call a vice, math calls a virtue. Meaninglessness, or lack of reference to anything tangible, is the heart of the power of mathematical abstraction.

As Wiles said when he proved Fermat's last theorem at a conference: "I think I'll stop now."

I don't think TonesInDeepFreeze quite has that attitude though — Metaphysician Undercover

Mote and Beam!

As Wiles said when he proved Fermat's last theorem at a conference: "I think I'll stop now." — fishfry

As Miles Davis said to producer Alfred Lion, "Is that what you wanted, Alfred?"

Or, just after Davis, Hancock, Carter and Williams laid down "Thisness" - an exceptionally gorgeous, introspective, haunting modern and abstract ballad - producer Teo Macero said to the group, "Your sandwiches are here."

You then stated that "we can only count representations of the imaginary things, which exist as symbols." — Luke

That's a false quote. I said "we are not really counting the imaginary things, but symbols or representations of them". You said they only exist as symbols, not I.

But I can't agree with your apparent extrapolation from that to an apparent rejection of all abstract math. — fishfry

What I look for, is points within abstract math where improvement is warranted.

I'm not enough of a physicist to comment. My point was only that you seemed to reject QM for some reason. I noted that you can't dismiss it so trivially, since QM has a theory -- admittedly fictional in some sense -- but that nevertheless corresponds with actual physical experiment to 13 decimal places. That's impressive, and one has to account for the way in which a fictional story about electrons can so accurately correspond to reality. Of course all science consists of historically contingent approximations. But lately some of the approximations are getting really good. Your dismissal seems excessive. — fishfry

The capacity to use mathematics to make very precise predictions does not necessarily indicate an understanding of the activity which is predictable. I often use as an example the capacity of ancient people to predict the position of the sun, moon, and planets, without understanding the orbits of the solar system. Thales apparently predicted a solar eclipse. So an ancient 'scientist' could predict the exact location the sun would rise on the horizon, and one could insist that this justifies a model which assumes that a dragon carries the sun in it's mouth around the earth from sun set to sunrise. Predicting the appearance of objects is completely different from understanding the activity involved.

FWIW I don't think anyone thinks the orbits are circular anymore. — fishfry

I know, that's the point. The concept of the magnetic moment of an electron is based in the assumption of a circular orbit, which is an idea known to be faulty. And the whole idea of "spin" in fundamental particles is not any sort of spin at all, because the particles cannot be shown to have any proper spatial area, within which to be spinning. The physicists simply apply the appropriate mathematics which produces the desired predictions, but the models which explain what the mathematics is doing are completely unacceptable, indicating that the physicists are capable of making predictions without knowing what is going on.

But you still have to account for the amazing agreement of theory with experiment. We might almost talk about the unreasonable effectiveness of physics in the physical sciences! — fishfry

That's the power of mathematics. But the experiments and the mathematics are designed for one another, so that the experiments show how good the mathematics is, and the mathematics shows how good the experimenters are. But they are only working with a very small portion of the microscale world, because of limited capacity for experimentation, and attempts to extrapolate show just how inadequate the mathematics, experiments, or both, are for producing a wider understanding.

I'm taking this from the end of your post and addressing it first to get it out of the way. As I mentioned, I didn't read any posts in this thread that didn't mention my handle. I only responded to one single sentence of yours to the effect that numbers are about quantity. I simply pointed out that there is another completely distinct use of numbers, namely order. Anything else going on in this thread I have no comment on. — fishfry

That is where I started in this thread, with the assertion that numbers are about quantity, but I've changed my mind twice since then. You got me to see the difference between quantity and order, and this difference is why I could not understand Tones' representation of counting as bijection. So, the act of "counting" may be an act of determining a quantity or it may be an act expressing an order. The two are very distinct as you say, but both are commonly referred to as "counting".

But if there are two distinct but related ways of using numerals, and each relates to the same concept "number", then we must proceed toward something further, some other idea which synthesizes the two, into one concept, "number". So I changed my mind again, in that post I asked you to reread I believe. What I said is that I think a number is "a value". This allows that the same value, expressed as "2" for example, can be assigned to a quantity of two, and also to the second in order. Remember what I said about a value. When we say "the same value", there is an equality between two distinct things without saying that the two things are the same thing (as implied by the law of identity).

Here's the quote from that post:

I think this helps to demonstrate that we cannot define numbers with counting. So, my original assumption that "2" implies a specified quantity of objects, must be false. But now we have the question of what does "2" mean? I think it is a sort of value, and by my statement above, a value we assign to empirical observations. However, if we can assign such a value to imaginary things in a similar way, we need a principle to establish equality, or compatibility, between observed things and imaginary things. This is required to use negative numbers. — Metaphysician Undercover

I may not be fully aware of the philosophical context of your use of "a priori." Do you mean mathematical abstraction? Because I am talking about, and you seem to be objecting to, the essentially abstract nature of math. The farmer has five cows but the mathematician only cares about the five. The referent of the quantity or order is unimportant. If you don't believe in abstraction at all (a theme of yours) then there's no hope. In elementary physics problems a vector has a length of 3 meters; but the exact same problem in calculus class presents the length as 3. There are no units in math other than with reference to the arbitrarily stipulated unit of 1. There aren't grams and meters and seconds. — fishfry

Surely I believe in abstraction, but all abstractions are derived (abstracted) from somewhere, unless they are completely innate. So the abstractions "quantity", and "order" must have some sort of referent themselves which give meaning to the concept. It does not make any sense, even in the context of pure mathematics, to say that there is a quantity of 5 which does not consist of five units. That's the meaning of "a quantity of 5". Even in abstraction there are necessary aspects of the concept which must be fulfilled to account for the meaning of the abstraction. If you are simply talking about "the number 5", and not a quantity of five, then we must look to see what gives "the number 5" its meaning., when it is supposed that it does not signify 5 discrete units. We might suppose that the meaning of "the number 5" is found in an order, it's the fifth. But the number 5 is not necessarily the fifth, and that's why I turned at first, to quantity to see how "the number 5" gets its meaning.

There's no time or space, just abstract numbers. I don't know how to say it better than that, and it's frustrating to me that you either pretend to not believe in mathematical abstraction, or really don't. — fishfry

This is not true, because the numbers have meaning, that's the point. You cannot use the number 5 however you please, and say "5+5=8". That is restricted by the meaning. So it's not simply "abstract numbers", it's specific numbers. Each number has its specific meaning or else all numbers would be the same. And when I look at the meaning of any specific number I find that the number either refers to spatially distinct units, 5 of them, or it refers to a temporal order, the fifth. Clearly there is time and space implied with abstract numbers, or else each number would lose its meaning which is specific to it.

You seem to want to deny the ideas themselves simply because they're abstract. That's the part of your viewpoint I don't understand. — fishfry

I do not want to deny the ideas, I want to understand them. And understanding them is what requires spatial and temporal reference. The number 5 has no meaning, and cannot be understood without such reference.

There is no need for time or space in math. I can't talk or argue or logic you out of your disbelief in human abstraction. — fishfry

An abstraction must be intelligible or else it is meaningless, useless. If it can't be understood without spatial or temporal reference, then there clearly is a need for space and time in math, or else all mathematics would be simply unintelligible.

You just phrase things like that to annoy me. How can you utterly deny human abstractions? Language is an abstraction. Law, property, traffic lights are abstractions. So is math. — fishfry

I do not deny human abstractions, I just insist that they are fundamentally distinct, different from objects. An object is a unique particular. An abstraction is a generalization. The two are very different from each other, and ought not be both classed together in the same category as "objects".

The notation is only suggestive of a deeper abstract truth, that of the idea of an endless progression of things, one after the next, with no end, such that each thing has an immediate successor. — fishfry

Do you agree that this order, "an endless progression of things, one after the next" is a temporal order?

Now the set of natural numbers N={0,1,2,3,4,…}N={0,1,2,3,4,…} has no inherent order. — fishfry

You'll have to do better than a simple assertion here. To say that the natural numbers have no inherent order, is to remove "order" as a defining feature of the natural numbers. Now we are left with quantity as the defining feature. Do you agree? There must be something which gives 5 and 6 meaning, if it's not a specific order, it must be a quantity. So we are not talking about an endless progression of things when we talk about the natural numbers in this way, we are talking about specific symbols, "1", "2", "3", etc., which represent specific quantities. Now we don't have a set of natural numbers, because we have no things, only symbols representing quantities. So the rest of your discussion of order is irrelevant. You have nothing to order, and no order to offer.

You then stated that "we can only count representations of the imaginary things, which exist as symbols."
— Luke

That's a false quote. I said "we are not really counting the imaginary things, but symbols or representations of them". You said they only exist as symbols, not I. — Metaphysician Undercover

Nope.

we can only count representations of the imaginary things, which exist as symbols. — Metaphysician Undercover

Luke, learn how to read! The representations, (which is what we count), exist as symbols. I did not say that the imaginary things exist as symbols. You've taken the sentence out of its context so that it appears possible that I might be saying what you claim to interpret. Though context clearly shows otherwise. This is exactly what I mean, you interpret, and represent what I say, in a totally incorrect (not what I intended), strawman way, solely for the purpose of knocking it down. Your MO, to ridicule, is itself ridiculous.

Luke, learn how to read! The representations, (which is what we count), exist as symbols. I did not say that the imaginary things exist as symbols. You've taken the sentence out of its context so that it appears possible that I might be saying what you claim to interpret. Though context clearly shows otherwise. This is exactly what I mean, you interpret, and represent what I say, in a totally incorrect (not what I intended), strawman way, solely for the purpose of knocking it down. Your MO, to ridicule, is itself ridiculous. — Metaphysician Undercover

You're just going to gloss over your accusation that I misquoted you, and the fact that I didn't?

I never took your position to be that "imaginary things exist as symbols [and representations]". Quite the opposite. This was, instead, the point I was trying to make and what I was trying to get you to understand. Perhaps you should learn to read.

When counting sheep, the imaginary sheep have no existence other than as imagined sheep. The imagined sheep are representations of real sheep, but they only exist as representations. That is to say, for example:

imaginary things only exist as their symbols or representations, and if we are really counting those symbols or representations, then we are really counting the imaginary things. — Luke

imaginary things have no existence other than their symbols or representations — Luke

There don't need to be any real sheep in order to make the count. One could as easily count unicorns instead of sheep. Or Enterprise captains. Or any other fictional entities.

So do philosophers have to accept the actual infinite? — spirit-salamander

If you ask me, we need to look at scientifically-confirmed physical limits. Take, for example, the speed of light. It is finite of course at 186,000 mph but nothing can attain that speed. Doesn't this bear an uncanny resemblance to infinity as something unattainable. This is, in my humble opinion, one of the many ways, infinity manifests itself in the universe. I like to call it, as oxymoronic as it sounds, finite infinity - the speed of light is finite but it's infinity as nothing can attain it.

There don't need to be any real sheep in order to make the count. One could as easily count unicorns instead of sheep. Or Enterprise captains. Or any other fictional entities. — Luke

As I said, that's an order, one imagined thing after the other, it's not a quantity.

As I said, that's an order, one imagined thing after the other, it's not a quantity. — Metaphysician Undercover

How is it that we can (really) order imaginary things, but we cannot (really) count imaginary things?

The category theoretic description of the natural numbers does away with the pesky elements of the natural number "set" and externalises the notion of 'element' onto the objects counted.



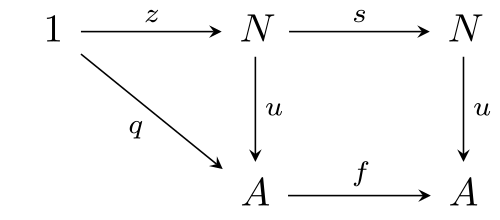
https://en.wikipedia.org/wiki/Natural_numbers_object

And so the notion of elements isn't needed for the pure purpose of constructing abstract numbers.

Does that help?

Does that help? — sime

:roll:

Category theory is a popular mathematical area. An offshoot of algebra, it can be used as an alternative to establish the foundations of math. It searches for so-called universal properties in various categories. Personally, I find it alien and entirely non-productive in the nitty gritty stuff I study in complex variables.

The Wikipedia page for Category theory gets 575 views/day, a respectable number. The page you linked gets 5 views/day and is classified as low priority (like my math page). So it may not help. But good try.

How is it that we can (really) order imaginary things, but we cannot (really) count imaginary things? — Luke

If "count" is defined as determining the quantity of, then it is an act of measuring. We can't measure imaginary things. But we can describe an order without requiring that measurable things exist in that order, the order itself is imaginary.

If "count" is defined as determining the quantity of, then it is an act of measuring. — Metaphysician Undercover

You are saying that counting is the same as measuring, but that can’t be right. Otherwise, what unit of measurement do we use to count? Litres? Metres? Hours? Bananas?

Or, just after Davis, Hancock, Carter and Williams laid down "Thisness" - an exceptionally gorgeous, introspective, haunting modern and abstract ballad - producer Teo Macero said to the group, "Your sandwiches are here." — TonesInDeepFreeze

Immediately before JFK was assassinated on November 22, 1963, Nellie Connolly, wife of Texas governor John Connolly, sitting in the seat in front of JFK in the presidential limo, turned around and said to JFK, "You can't say that Dallas doesn't love you, Mr. President."

You have nothing to order, and no order to offer. — Metaphysician Undercover

LOL There's a famous off-color joke with a very similar punchline, but nevermind.

To say that the natural numbers have no inherent order, is to remove "order" as a defining feature of the natural numbers. — Metaphysician Undercover

I would use the word "abstract" rather than "remove." The point is that by abstracting the concept of order from any particular meaning, we can better study order. That's the entire point of my post, which, if it didn't help, didn't help. The point of abstraction is to take away meaning such as first base, second base, so that we can study first and second abstracted from meaning. That doesn't make abstraction meaningless, it just means that we use abstraction to study concrete things by abstracting away the concreteness.

Now we are left with quantity as the defining feature. Do you agree? — Metaphysician Undercover

Well, yes and no. Von Neumann's coding of the natural numbers has the feature that the cardinality of the number n is n. But there are other codings in which this isn't true, for example 0 = {}, 1 = {{}}, etc. So we can abstract away quantity too if we like. But that wasn't the point, Even if I grant you that cardinality provides a natural way of ordering the natural numbers, it's still not the only way.

Anyway I did my best and don't think I can add anything.

I do not deny human abstractions, I just insist that they are fundamentally distinct, different from objects. — Metaphysician Undercover

I get that you don't believe in mathematical "objects." What do you call them then? What do you call numbers, sets, topological spaces, and the like?

I do not want to deny the ideas, I want to understand them. And understanding them is what requires spatial and temporal reference. The number 5 has no meaning, and cannot be understood without such reference. — Metaphysician Undercover

Obviously the abstract mathematical object (oops there's that phrase again) 5 is derived or inspired by the familiar concept of 5. Sort of like Moby Dick, which is entirely fictional, was inspired by an actual whaleboat, the Essex, that was sunk by a whale.

But the 5 that mathematicians study is indeed an abstract object. It's not 5 oranges or 5 planets or 5 anything. It's just 5. That's mathematical abstraction. I guess I'm all out of explanations.

An abstraction must be intelligible or else it is meaningless, useless. If it can't be understood without spatial or temporal reference, then there clearly is a need for space and time in math, or else all mathematics would be simply unintelligible. — Metaphysician Undercover

There is no space or time in math. Why can't you accept abstraction? There's space and time in physics, an application of math. There's no space or time in math itself. Is this really a point I need to explain? What am I missing that would let me get through to you on this point? A physicist cares about 5 meters or 5 seconds. The mathematician only cares about 5. It's cardinality, its ordinality. It's role as a natural number, an integer, a rational, or a real number. Its primality. What is the thing on which you and I disagree regarding this?

And so the notion of elements isn't needed for the pure purpose of constructing abstract numbers. — sime

It's certainly interesting that one can do set theory without elements.

Category theory is a popular mathematical area. An offshoot of algebra, it can be used as an alternative to establish the foundations of math. It searches for so-called universal properties in various categories. Personally, I find it alien and entirely non-productive in the nitty gritty stuff I study in complex variables.

The Wikipedia page for Category theory gets 575 views/day, a respectable number. The page you linked gets 5 views/day and is classified as low priority (like my math page). So it may not help. But good try. — jgill

I'm unsurprised that you dislike CT. Abandoning elements feels a bit like abandoning nouns in ordinary language. It isn't a coincidence that the Turing Machine has been the predominant model of computing over the Lambda calculus - the modular conceptualisation of systems in terms of reusable and independently existing entities or elements is cognitively and practically expedient relative to the holistic structuralism of type theory/CT, albeit at the mere cost of potential philosophical confusion.

Although in the case of comp-sci, the practical expedience has recently moved towards CT due the shift to multi-core parallel programming, where control flows can be containerized, layered and equalized in a logically concise fashion using Monads. I also suspect that some generalisation of CT will become important to AI and machine learning over the next few years, due to it's notational emphasis on processes and interaction.

If nothing else, CT serves as an elitist language for getting ahead in the programming jobs market.

Nice reply. Thanks.

You are saying that counting is the same as measuring, but that can’t be right. Otherwise, what unit of measurement do we use to count? — Luke

Counting is not "the same as measuring", it's a form of measuring. What is required for measuring is a standard, The standard for counting is "the unit", which is defined as an individual, a single, a particular. So in measuring a quantity (counting) we must make a judgement as to what qualifies as a unit to be counted.

The point is that by abstracting the concept of order from any particular meaning, we can better study order. — fishfry

OK, so you define "order" as "having no meaning". That is your starting premise? What's the point? Any meaning you give to it will be logically invalid, as contradictory to that definition. There is nothing to study in a concept which has no meaning.

The point of abstraction is to take away meaning such as first base, second base, so that we can study first and second abstracted from meaning. That doesn't make abstraction meaningless, it just means that we use abstraction to study concrete things by abstracting away the concreteness. — fishfry

Of course it makes it meaningless, you just said you take away meaning from it. If you take away all the meaning from "first" and "second", you just have symbols without meaning. If you leave some sort of meaning as a ground, a base, you have a temporal reference, first is before, (prior to) second.

You are using "abstract" in a way opposite to convention. We do not "take away meaning" through abstraction, abstraction is how we construct meaning. There is a process called "abstraction", by which we remove accidental properties to give us essentials, what is necessary to the concept. We do not abstract away the meaning, we abstract what is judged as "necessary" from the concreteness, leaving behind what is unnecessary, "accidental".

Well, yes and no. Von Neumann's coding of the natural numbers has the feature that the cardinality of the number n is n. But there are other codings in which this isn't true, for example 0 = {}, 1 = {{}}, etc. So we can abstract away quantity too if we like. But that wasn't the point, Even if I grant you that cardinality provides a natural way of ordering the natural numbers, it's still not the only way. — fishfry

Sure, cardinality is not the only possible way of ordering numbers, but if the point is, as you described, to allow for any possible order, then we have to deny the necessity of all possible orders. That is to say that there is no specific order which is necessary. This removes "order" as a defining feature of numbers, because no order is necessary, so numbers do not inherently have order. Therefore order is not essential to the concept of numbers Then, we need something else to say what makes a number a number, or else we just have symbols without meaning.

We could try saying that it is necessary that numbers have an order, but the specific order which they have is not necessary, like we might say a certain type of thing must have a colour, but it could be any colour. But this will prove to be a logical quagmire because it's really just a way of smuggling in a contradiction. It is impossible, by way of contradiction, that something must be a specific colour, and at the same time is possibly any colour. It is only possible that it is the colour that it is. Likewise, it is impossible that numbers must have a specific order, but could possibly be any order, because the order that they currently have, would restrict the possibility of another order.

The point was, that if remove all order, to say that numbers are not necessarily in any order, then we must define the essence of numbers in something other than order. If this is cardinality, then cardinality is not an order.

What do you call numbers, sets, topological spaces, and the like? — fishfry

They are concepts, abstractions. I apprehend a difference between concepts and objects, because concepts are universals and objects are particulars. There is an incompatibility between the two, and to confuse them, or conflate them is known as a category mistake.

But the 5 that mathematicians study is indeed an abstract object. It's not 5 oranges or 5 planets or 5 anything. It's just 5. That's mathematical abstraction. I guess I'm all out of explanations. — fishfry

It's an idea, and ideas are not objects. I have an idea to post this comment, and this idea exists as a goal. Goals are "objects", or objectives, in a completely different sense of the word. So if you want to say that numbers, as ideas are "objects", we'd have to look at this sense of the word, goals. But it doesn't make too much sense to say that they are objects in this sense, nor does it make any sense at all, to say that numbers, as ideas, are objects in the sense of particulars, because they are universals.

There is no space or time in math. Why can't you accept abstraction? There's space and time in physics, an application of math. There's no space or time in math itself. Is this really a point I need to explain? — fishfry

Space and time are themselves abstractions, and these concepts very clearly enter into, and are fundamental to mathematics. Are a circle and a square not a spatial concept, which are mathematical? Is the order of first, second, third, fourth, not a temporal order whish is mathematical? If you seriously think that you can separate mathematical concepts from spatial and temporal concepts, then yes, this is something you really need to explain, because I've been trying to do it for many years and cannot figure out how it's possible. So please oblige me, and explain.

The mathematician only cares about 5. — fishfry

The problem is that "5" means nothing without a spatial or temporal reference. If you think that the mathematician believes that "5" refers simply to the number 5, without any further reference to give the concept which you call the number 5 meaning, then you must believe that mathematicians think that the number 5 is a concept of nothing.

It's certainly interesting that one can do set theory without elements. — fishfry

If I'm not mistaken, Von Neumann formalized without 'element' as primitive in 1925.

If I'm not mistaken, Von Neumann formalized without 'element' as primitive in 1925. — TonesInDeepFreeze

Would be most interested in a reference or more context.

Counting is not "the same as measuring", it's a form of measuring. What is required for measuring is a standard, The standard for counting is "the unit", which is defined as an individual, a single, a particular. — Metaphysician Undercover

You have it backwards.

The standard for counting is "the unit".
The standard for measuring is "the unit of measurement".

What unit of measurement is required for counting the natural numbers? Metres? Litres? Hours? Bananas? Obviously, no unit of measurement is required. You can count to ten without having to determine any unit of measurement. Therefore, counting is independent of measuring. Counting is not a "form of" measuring.

↪jgill

I'm unsurprised that you dislike CT. — sime

@jgill does complex analysis, where CT has made few if any inroads. The theory of fields doesn't make for a good category, as I've heard it put, so the analysts haven't been categorified as the algebraists have.

What unit of measurement is required for counting the natural numbers? Metres? Litres? Hours? Bananas? Obviously, no unit of measurement is required. You can count to ten without having to determine any unit of measurement. Therefore, counting is independent of measuring. Counting is not a "form of" measuring. — Luke

@Metaphysician Undercover, What he said.

OK, so you define "order" as "having no meaning". That is your starting premise? What's the point? Any meaning you give to it will be logically invalid, as contradictory to that definition. There is nothing to study in a concept which has no meaning. — Metaphysician Undercover

Excellent job of misquoting me, attributing to me things I didn't say, and launching yourself into another irrelevant tirade against math, or abstraction, or the ordinal numbers, or whatever it is you're against.

Perhaps you're right that meaning isn't the correct word. If I said we remove a concept from its worldly or physical referent, would that be better? We care about first, second, third, and not first base, second base, third base. So how would you describe that? I'm focusing on ordinality itself and not the things ordered. So you're right, meaning was an imprecise word.

Of course it makes it meaningless, you just said you take away meaning from it. If you take away all the meaning from "first" and "second", you just have symbols without meaning. — Metaphysician Undercover

We have order, without reference to the things ordered. We still have meaning, I'll concede that meaning was the wrong word. What would would you use?

If you leave some sort of meaning as a ground, a base, you have a temporal reference, first is before, (prior to) second. — Metaphysician Undercover

There is no temporal reference.

You are using "abstract" in a way opposite to convention. We do not "take away meaning" through abstraction, abstraction is how we construct meaning. — Metaphysician Undercover

No not at all. One meter, one fish, one planet is meaning. One by itself is a mathematical abstraction. I'm not entirely sure that it means anything now that you mention it. But we can still study it, and then apply what we learn in the abstract setting to any particularities of interest.

There is a process called "abstraction", by which we remove accidental properties to give us essentials, what is necessary to the concept. We do not abstract away the meaning, we abstract what is judged as "necessary" from the concreteness, leaving behind what is unnecessary, "accidental". — Metaphysician Undercover

Ok. I agree that I'm having trouble precisely defining abstraction and I sort of see your point. But ordinal numbers are purely about order, but they're not about any particular things being ordered. How would you describe that? It's not meaningless, yet it refers to nothing in the world at all other than the pure concept of order. Which you don't seem to believe in.

Sure, cardinality is not the only possible way of ordering numbers, but if the point is, as you described, to allow for any possible order, then we have to deny the necessity of all possible orders. — Metaphysician Undercover

No, although we do deny the primacy of any particular order. That is, in order theory, the usual order 1, 2, 3, ... is no more important or special than one of the funny orders like 1 2, 4, ..., 3. Although the 1, 2, 3, ... order is important enough to give it a name, the "standard order" or "usual order" on the natural numbers. But you are correct that in order theory, the process of abstraction does put us in the position of regarding all possible orders as equally valid. Not unlike lining up the schoolkids by height, by alpha last name, by reverse alpha first name, by date of birth, by test score, etc. Each of those orders is equally valid in some particular context, and none is inherently preferred over any other. Right? Surely you'll grant me that. And then further grant me that mathematically, sometimes the usual order on the natural numbers is useful (like in most ordinary usages of math), and other times alternate orders are (like when studying or using the higher ordinals).

That is to say that there is no specific order which is necessary. — Metaphysician Undercover

Correct correct correct. Although I suspect you're about to object to that! But yes, that is exactly right. One order is as valid as another if we're studying pure order theory; although we DO honor the grade school teachers of the world by giving 1, 2, 3, ... a special name, the standard or usual order.

This removes "order" as a defining feature of numbers, — Metaphysician Undercover

Absolutely correct. I think you're trying to disprove or invalidate the idea, but actually you're understanding the process perfectly.

because no order is necessary, so numbers do not inherently have order. — Metaphysician Undercover

Correct correct correct. One order is as good as another, though the standard order has considerable mindshare among the general public and of course among mathematicians too. I'd be pushing the point too far if I denied that the standard order is special. After all in the standard order, the numbers are arranged by cardinality, which important; and the ordinals are arranged by set membership, whichis also important. So yes there IS in fact a "natural" way of characterizing the standard order is important.

Therefore order is not essential to the concept of numbers — Metaphysician Undercover

Just as being lined up by height is not essential to the concept of school children. Being orderable in one or many ways is an attributed of children and numbers, but it is not essential to the concept.

Then, we need something else to say what makes a number a number, or else we just have symbols without meaning. — Metaphysician Undercover

The question of what is the meaning of numbers is an interesting one. I'm not sure mathematicians concern themselves about it, just like biologists don't spend much time talking about the meaning of cells, or physicists (when they are doing physics) talk about the meaning of quarks. When physicists are doing philosophy, they talk about the meaning of quarks. And when mathematicians are doing philosophy, perhaps they talk about the meaning of numbers. But even on that last point, I'm not too sure.

I don't know what numbers "mean." I had dinner earlier and I don't know what my dinner meant. I know it tasted good. Is that a problem, that I don't know the meaning of dinner? What do you even mean by meaning in this context?

We could try saying that it is necessary that numbers have an order — Metaphysician Undercover

It isn't. We could consider the set $\mathbb N$ of natural numbers, which has no particular order at all, or that implicitly comes along by convention with its standard order. But order is not essential to numbers, it's imposed afterward. At least in the mathematical formalism. I get that you are drawing a distinction between the mathematical formalism, in which order is secondary to the existence of numbers; and philosophy, in which order is an essential aspect of numbers.

But in the Peano formulation, order is inherent via the successor relation. In the past you've rejected the Peano axioms, but now it seems that you should be happy with them. Because in Peano arithmetic we have 0, and we have S0, and then SS0, and then SSS0, and so forth, and there is an inherent order to the process. Happy now?

, but the specific order which they have is not necessary, like we might say a certain type of thing must have a colour, but it could be any colour. — Metaphysician Undercover

A schoolkid must have a height, but it could be any height. But with numbers it's even worse than that. A set of numbers, like a set of anything, has no inherent order. Order is a relation imposed upon a set. The set is logically prior to the order. Yes you are right about that, and I get that you're unhappy about that, but that's how it is. At least in the modern formulation of these matters.

But this will prove to be a logical quagmire — Metaphysician Undercover

You see it that way. I see it as providing beautifully logical clarity. We have the set of natural numbers, and we have the standard order and we have a lot of other orders, and we can even consider the entire collection of all possible orders, which itself turns out to be a very interesting mathematical object. It's quite a lovely intellectual structure. I'm sorry it gives you such distress.

because it's really just a way of smuggling in a contradiction. — Metaphysician Undercover

A contradiction is a proposition P such that both P and not-P may be proven from the axioms. Perhaps you would CLEALY state some proposition whose assertion and negation are provable from the concept of order as I've presented it. I don't think you can.

I would believe that you have some philosophical unease. That's not the same as a contradiction. Can you see that?

It is impossible, by way of contradiction, that something must be a specific colour, and at the same time is possibly any colour. — Metaphysician Undercover

But I have not asserted that a set must have any order at all. The set $\mathbb N$ has no inherent order at all. Just like a classroom full of kids has no inherent order till the teacher tells them to line up by height or by alpha firstname or reverse alpha lastname or age or test score or age. Why can't you see that?

A set has no inherent order. Order is imposed on a set afterward, and only for our own convenience in a given context. Sometimes one order, sometimes another, depending on what we're trying to achieve or express.

It is only possible that it is the colour that it is. — Metaphysician Undercover

Terrible analogy. Physical objects have color, but sets don't have an inherent order. Besides I could play the game of pointing out that while physical objects reflect light of a particular wavelength, their color is a function of the physiology of the visual system of the perceiver. So the color isn't really inherent in the object.

But I won't go there. Rather, I will just note that physical objects do have color (or at least a wavelength that gets reflected when it is hit with white light), and mass, and electric charge, and various other physical parameters. But sets do not have inherent order and this is absolutely fundamental to the nature of sets. Axiom of extensionality again: A set is completely characterized by its elements. Order has nothing to do with it, and a set by itself has no inherent order at all.

Likewise, it is impossible that numbers must have a specific order, but could possibly be any order, because the order that they currently have, would restrict the possibility of another order. — Metaphysician Undercover

Not at all, and I've shown you the example several times. The order sets $(\mathbb N, \lt)$ and $(\mathbb N, \prec)$ are the same underlying set of elements, each with a different order. Neither order is inherent to the underlying set.

The point was, that if remove all order, to say that numbers are not necessarily in any order, then we must define the essence of numbers in something other than order. — Metaphysician Undercover

Absolutely agreed. Yes. The essence of a set of numbers is NOT in their order, since we can easily impose many different orders on the same underlying set. Just as the ordering by height is not essential to the classroom of kids, since we can impose a different order; or by letting them loose in the playground at recess, we can remove all semblance of order! Surely you must take this point.

If this is cardinality, then cardinality is not an order. — Metaphysician Undercover

Of course cardinality is not an order, I thought that was abundantly clear long ago. But yes we can order a set by cardinality, if the set consists of elements of distinct cardinality. We can do that. We can order the kids by height, if in fact their heights are all distinct. If two kids have the exact same height then we can't linearly order the class by height.

They are concepts, abstractions. — Metaphysician Undercover

Ok. But that's not good enough. I asked how do you call mathematical objects like topological spaces. But justice and property are concepts and abstractions, yet they are not mathematical objects.

If you don't like the phrase, "mathematical object," what do you call them? Sure they're an abstraction, but that's way too general. You see that I'm sure.

I apprehend a difference between concepts and objects, because concepts are universals and objects are particulars. There is an incompatibility between the two, and to confuse them, or conflate them is known as a category mistake. — Metaphysician Undercover

Ok. I call numbers, sets, topological spaces, Abelian groups, etc., by the collective name mathematical objects. What do you call them? You can't say "abstractions," because justice and property are abstractions that are not mathematical objects. Consider yourself challenged to come up with a better name, if you don't like "mathematical object."

It's an idea, and ideas are not objects. — Metaphysician Undercover

Ok. this is a difference between us. I say 5 is a mathematical object, a very familiar one. Relatively few people know what a topological space is, but every child knows what 5 is. You say it's an idea and not an object. I think you're wrong about that. But we've been arguing this point for a long time.

I have an idea to post this comment, and this idea exists as a goal. Goals are "objects", or objectives, in a completely different sense of the word. So if you want to say that numbers, as ideas are "objects", we'd have to look at this sense of the word, goals. — Metaphysician Undercover

An object is not a goal. An (American) football is an object, and the goal is to get it across the goal line. You would not say the football is a goal. I think you're way off the mark with your claim that an object is a goal or objective. 5 has no object or purpose. It's just the number 5. A mathematical object. An abstract object, as all mathematical objects are.

But it doesn't make too much sense to say that they are objects in this sense, nor does it make any sense at all, to say that numbers, as ideas, are objects in the sense of particulars, because they are universals. — Metaphysician Undercover

We disagree, since I say 5 is a mathematical object. And I don't think you have a good theory to the contrary. And 5 is a PARTICULAR mathematical object. A universal is a "... class of mind-independent entities ..." (Internet Encyclopedia of Philosophy). 5 is not a class of entities, it's a single entity. A mathematical object.

Space and time are themselves abstractions, and these concepts very clearly enter into, and are fundamental to mathematics. — Metaphysician Undercover

They don't exist anywhere in mathematics. Of course "space" is a technical term very commonly used in math, as in a topological space or Euclidean space or a Banach space etc. But space as conceived in physics, as well as time, do not exist in math. If you would carefully study the axioms of set theory, you will see no references to time or space. Of this I am quite certain.

Are a circle and a square not a spatial concept, which are mathematical? — Metaphysician Undercover

They're idealized geometric mathematical objects. There are no circles or squares in the world, only approximations to the mathematical ideal.

Is the order of first, second, third, fourth, not a temporal order whish is mathematical? — Metaphysician Undercover

No, not in the least. How can you say that? That's not even the meaning of the words in everyday speech in the real world. The winner takes first place and the runner up takes second place sometimes (as in a foot race) but not always (as in a weight lifting contest) by being temporally first. You must know this, why are you using such a weak argument? First place in golf goes to the player with the lowest score, not to the player who finishes the course first. This is a TERRIBLE argument you're making here.

If you seriously think that you can separate mathematical concepts from spatial and temporal concepts, then yes, this is something you really need to explain, — Metaphysician Undercover

No, the onus is on you, as space and time play no role in the axioms and principle of mathematics.

because I've been trying to do it for many years and cannot figure out how it's possible. — Metaphysician Undercover

If you stop confusing math and physics you will be enlightened.

So please oblige me, and explain. — Metaphysician Undercover

Space and time have nothing to do with mathematics. Show me where it says they do. Look up the axioms of set theory (here for instance) and show me time and space. They're not there.

Nor are they even philosophically a part of math. A physicist has 5 meters or 5 seconds. Math just has the number 5. I hope you weren't fooled by grade school when they tell you that Sally had 5 apples and Fred had 3 apples, how many apples do they have together? Once you get past that level, they just ask you to add 5 plus 3. The apples are part of physics or biology or grocery store management. Applications of math, not math.

The problem is that "5" means nothing without a spatial or temporal reference. — Metaphysician Undercover

If I ask you if 5 is prime, can you answer? How did you do that? Did you really have to mentally imagine 5 apples?

If you think that the mathematician believes that "5" refers simply to the number 5, without any further reference to give the concept which you call the number 5 meaning, then you must believe that mathematicians think that the number 5 is a concept of nothing. — Metaphysician Undercover

No, it's the mathematical object 5. It's the third prime number. It's the order of the group of integers mod 5, and the number of sides of a pentagon. It's the largest positive integer such that all groups of order less than or equal to it are Abelian. That property uniquely characterizes the number 5. Martian mathematicians must necessarily have the same theorem. Likewise the Martians must know that there is no algebraic formula to solve a polynomial equation of degree 5 having integer coefficients. Any sentient race anywhere in the universe must necessarily discover this sooner or later.

Mathematicians have many concrete, if you'll permit that use of the word, ideas and concepts about the abstract mathematical object 5. They can represent it within set theory as a natural number, an integer, a rational, a real, a complex number, or a quaternion. Each such representation is a distinct set. We can identify them all via standard conventions. These representations might NOT be used by Martian mathematicians. The representations are contingent, but the facts about the number 5 are not. Mathematicians could write a dissertation on 5. Wikipedia has a relatively long article on the number 5. And that ain't nothing!

If I'm not mistaken, Von Neumann formalized without 'element' as primitive in 1925.
— TonesInDeepFreeze

Would be most interested in a reference or more context. — fishfry

The original paper is in Jean van Heijenoorts's 'From Frege To Godel'.

Wikipedia has a relatively long article on the number 5. — fishfry

And it's even classified as Vital. There must be 10K pages on math on Wiki. I wonder how many are added each day?