-
 TonesInDeepFreeze
3.8kThat's a very modest claim.
TonesInDeepFreeze
3.8kThat's a very modest claim.
That there is a recursive axiomatization of a theory T entails that it is computable whether any given string is or is not an axiom.That follows from the fact that any recursive relation is computable.
By the way, I don't know what would be the value in telling others that I said it, since I am not in any way an authoritative expert in logic of mathematics. The only thing I really know very much about is jazz. -
 Shawn
13.5k
Shawn
13.5k
I got this reply, which is really interesting for me to understand:
The real key to Gödel is that the axioms are recursively enumerable, not countable. We can show there exist maximal consistent subsets of the countable set of all statements, and take those as axioms. Then we can show that maximality implies completeness. It’s just not useful for human or computer-read proofs, because there is no way to algorithmically prove each step is allowed.
What do you think @jgill, and @TonesInDeepFreeze? -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Here, 'computable' is to be taken as 'Turing machine computable'.
"If R is recursive then R is Turing machine computable".
That has a long and complicated proof, but it's not controversial that it is proven.
Note that this does not even need to assume the Church-Turning thesis, as its converse ("If R is recursive then R is computable (in an intuitive informal sense of 'computable')") is not controversial. -
 TonesInDeepFreeze
3.8kan axiom I understand here is an expression, like Godel's sentence, such that neither it nor its negation is provable, yet is also provably true, being proved meta-mathematically — tim wood
TonesInDeepFreeze
3.8kan axiom I understand here is an expression, like Godel's sentence, such that neither it nor its negation is provable, yet is also provably true, being proved meta-mathematically — tim wood
That is incorrect. You have conflated "formula F is independent of axiom set S" with "formula F is an axiom in the axiom set S".
Axiomatization is a relation between a set of sentences (called 'the axioms') and the set of sentences (called 'the theorems') that are provable from those axioms. I.e.:
A set of sentence S is an axiomatization of a set of sentences T iff every member of T is provable from some finite subset of S.
A theory is a set of sentence closed under deduction (provability).
A recursive axiomatization S of a theory T is a recursive set of sentences S such that every member of T is provable from a finite subset of S.
Trivially, any axiom in S is provable from S. (Trivially, any axiom is provable from itself.)
A theory T is recursively axiomatizable iff there is a recursive set S that is an axiomatization of T.
/ -
 Shawn
13.5kHere's the other question asked just for fun:
Shawn
13.5kHere's the other question asked just for fun:
https://math.stackexchange.com/questions/4142390/completeness-without-uncountability -
 TonesInDeepFreeze
3.8krecursively enumerable is not the same as recursive, and implies non-recursiveness. — tim wood
TonesInDeepFreeze
3.8krecursively enumerable is not the same as recursive, and implies non-recursiveness. — tim wood
That is incorrect.
It is an easy theorem that R is recursive iff (R is recursively enumerable & ~ R is recursively enumerable).
A recursive enumeration does not itself provide a decision procedure for R, but that does not entail that there does not exist a decision procedure for R. -
 TonesInDeepFreeze
3.8kWhat do you think — Shawn
TonesInDeepFreeze
3.8kWhat do you think — Shawn
I would have to think it through. I am simply not caught up in the StackExchange thread. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
The very first sentence in the very first reply to you in that thread:
"What does it mean for a theorem to be complete or uncountable?"
Please stop using the phrases "theorem is complete" or "theorem is countable". They make no sense, and all they do is make people have to stop you in your tracks before we can even answer you about anything else you ask or say. -
 TonesInDeepFreeze
3.8ka recursive set is not the same thing as a recursively enumerable set, — tim wood
TonesInDeepFreeze
3.8ka recursive set is not the same thing as a recursively enumerable set, — tim wood
In the exact sense that the set of recursive sets is a proper subset of the set of recursively enumerable sets.
closure — tim wood
A theory is closed under deduction.
But the clause you have in mind is recursive axiomatizability. (I don't think that is usually referred to as 'closure'.) -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
At least for now, I've decided not to post there. There are already too many confusions in the discussions, and I'm not up to sorting through them with the participants. Also, I don't like the interface and layout of the post and thread formatting there. -
 jgill
4kCan you explain this, as I'm quite interested? — Shawn
jgill
4kCan you explain this, as I'm quite interested? — Shawn
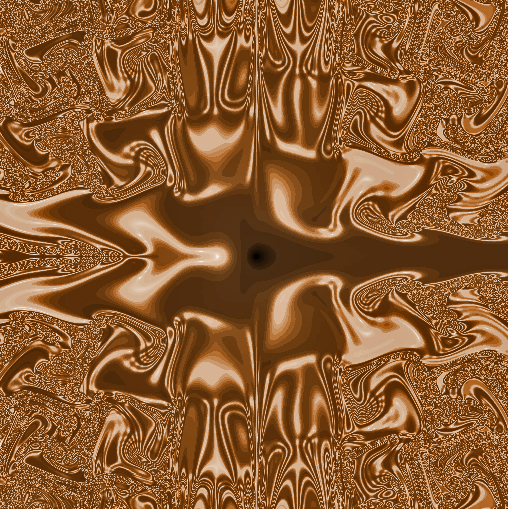
Well, Shawn, you asked for it. Sorry, buddy, it's convoluted and I doubt comprehensible. I don't usually go to professional math sites like StackExchange, preferring to do the job myself, but I don't think it would make any difference for this particular problem. So I'll put it up here. And one of the math people on the forum might have a suggestion:
Start with a sequence of complex functions: ,
And create a second sequence: , Which can be written as:
Then show exists.
There have been discussions on this thread about recursive objects. Here's a Lulu from actual math, not about math. :cool:
This dynamical system is associated with an image I will post. -
 Shawn
13.5k@TonesInDeepFreeze,
Shawn
13.5k@TonesInDeepFreeze,
I've been wondering if the question posted over at StackExchange, is generalizable?
What do you think? -
 Shawn
13.5kI'm also trying to figure out whether the complexity class is determinate for the first question I asked on StackExchange.
Shawn
13.5kI'm also trying to figure out whether the complexity class is determinate for the first question I asked on StackExchange.
https://math.stackexchange.com/questions/4144858/finding-the-shortest-proof-how-complex-is-it -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
First, for your questions, these still need to be clearly settled:
(1) Given a recursively axiomatizable theory with finitely many axioms, and with 'length of proof' defined as the sum of the lengths of the formulas that are the lines in the proof, is there an algorithm to determine. for any given theorem, the least length of a proof?
(2) Given a recursively axiomatizable theory with infinitely many axioms, and with 'length of proof' defined as the sum of the lengths of the formulas that are the lines in the proof, is there an algorithm to determine, for any given theorem, the least length of a proof?
(3) Given a recursively axiomatizable theory with finitely many axioms, and with 'length of proof' defined as the number of lines in the proof, is there an algorithm to determine, for any given theorem, the least length of a proof?
(4) Given a recursively axiomatizable theory with infinitely many axioms, and with 'length of proof' defined as the number of lines in the proof, is there an algorithm to determine, for any given theorem, the least length of a proof? -
 Shawn
13.5k
Shawn
13.5k -
 TonesInDeepFreeze
3.8kThose are my questions to sort out the discussion at StackExchange. You can post it if you want, but I probably won't follow up there or here, as I explained.
TonesInDeepFreeze
3.8kThose are my questions to sort out the discussion at StackExchange. You can post it if you want, but I probably won't follow up there or here, as I explained. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k -
 TonesInDeepFreeze
3.8khttps://thephilosophyforum.com/discussion/comment/539584
TonesInDeepFreeze
3.8khttps://thephilosophyforum.com/discussion/comment/539584
In all cases, it seems to me that, since we are concerned with finding the shortest proof, we only need to consider the finite part of the signature that occurs in the theorem, and we don't need to consider alphabetic variants.
(1) I think 'Yes'. There are only finitely many strings of a given finite length from a finite set of symbols, and only finitely many axioms to check whether a string is an axiom.
(2) I think 'Yes'. There are only finitely many strings of a given finite length from a finite set of symbols, and it is algorithmic to check whether any one of them is an axiom.
(3) I didn't check the details of the argument at
https://math.stackexchange.com/questions/1002618/how-to-find-the-shortest-proof-of-a-provable-theorem
that purports to show that the answer is 'No', but the poster seems to be knowledgeable.
(4) I didn't check the details of the argument at
https://math.stackexchange.com/questions/1002618/how-to-find-the-shortest-proof-of-a-provable-theorem
that purports to show that the answer is 'No', but the poster seems to be knowledgeable. And, aside from his argument, it does seem to make sense that if there are infinitely many axioms, then there are infinitely many different possible proof lines, so the algorithm could go on indefinitely before arriving at an answer. -
 Shawn
13.5kI kind of have this topic in mind again, and was thinking that if completeness cannot be determined for theorems, then can they be ascertained in complexity?
Shawn
13.5kI kind of have this topic in mind again, and was thinking that if completeness cannot be determined for theorems, then can they be ascertained in complexity?
It would be interesting to look into this as a general proposition.
What do you think, @TonesInDeepFreeze?
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum