-
TheMadFool
13.8kSquare Circle
A square circle would be a shape or object in Euclidean space that is both square and circular. Philosophers, especially working in philosophy of language and metaphysics, use the phrase "square circle" as an example of a contradiction in terms, that is, a phrase (as opposed to a proposition), two parts of which describe qualities that cannot both exist in the same thing at the same time.
It is also often used as an example of an "impossible object." Probably the most interesting philosophical question about square circles, and other such "impossible objects," is whether they enjoy any sort of existence or being. The 19th century German philosopher, Alexius Meinong, famously held that while such objects obviously do not exist, they nevertheless enjoy a queer sort of "being." Other philosophers have held that "square circle" is literally nonsense, that is, lacks any significance or meaning. An interesting feature of that position, however, is that it denies significance despite the fact that the words "square" and "circle" do individually have meaning, and we can say what their truth conditions are (i.e., necessary and sufficient conditions of their being true).
"Clever schoolboys" may point out that a three-dimensional shape may be square on one plane, and circular on an orthogonal plane. To their disappointment, philosophers stipulate that does not count as a square circle.
Note that this does not have to do with the geometrical problem of squaring the circle, that is, constructing a circle that has the same area as a square using only a compass and straightedge. — Citizendium
A square circle has become a byword for contradictions.
Contradiction: for p, a proposition, p & ~p.
Contradictions are strictly forbidden in classical logic (categorical, sentential, and predicate logic): Law Of Noncontradiction! because of Ex Contradictione [Sequitur] Quodlibet (The Principle Of Explosion)
Law of noncontradiction: for p, a proposition, ~(p & ~p)
2D = 2 Dimensional (space/world)
3D = 3 Dimensional (space/world)
Consider now a 3D object, a right cylinder with height 4 units and diameter 4 units. Depending on the angle of the light you shine on it, the shape of its shadow will change. If you try every possible angle you should get the following two shadow shapes:
1. A square with sides 4 units
2. A circle with diameter 4 units
Note these shadows are cast on a flat surface i.e. the square and the circle are two distinct 2D projections of the aforementioned 3D cylinder with height 4 units and diameter 4 units.
Mutually contradictory propositions (a square & a circle) could be shadows (Plato's Allegory Of The Cave) of propositions (3D cylinder) that exist in higher dimensions.
Taking this a step further, have a look at nets. The aforementioned 3D cylinder can be cut along its height and unfolded to yield a 2D rectangle with width = 4 units and length = the circumference of the circle (approx. 12.57 units).
In summary, propositions that we know of in this world, could be transported to a higher level world, given a twist, the resultant higher level proposition projected back onto our world as a contradictory propositions.
Basically: Proposition T in our world (2D rectangular net) -> Taken to a higher world (3D) -> T given a twist (3D cylinder/T') -> Projected back into our world as two mutually contradictory propositions (S/a square & ~S/a circle).
P. S. Go wild with dimension.
Addendum 1
The 3D cylinder T' (1 single 3D dimensional proposition) casts 2 fundamentally different 2D shadows S, square and ~S, circle (2 contradictory 2D propositions). As litewave remarked, it's about perspective - from a certain point of view, the proposition S is true and from another the contradictory proposition ~S is true.
~S is, as is obvious, the negation of S and without perspective to sort things out, we would've been left scratching our heads with the contradiction S & ~S.
Now, consider us (2D world denizens) trying to come to terms with the mutually incompatible claims about our world, S and ~S. We could assume a higher/deeper reality/world which contains the claim (3D proposition T'). How can we discover T'? My best guess is to imagine the various 3D shapes that could cast a square shadow/S (cube, cylinder, to name a few) and a circular shadow/~S (cone, sphere, cylinder, etc.). Which 3D shape is common to both sets? The cylinder of course and just like that we've discovered a 3D proposition that matches the shadows cast in our 2D world.
In plain English, we can discover truths about, how shall I put it?, higher realities if only we don't consider contradictions (p & ~p) as false but treat both p and ~p as true albeit from different angles.
Take theism vs atheism. The former claims that God exists while the latter claims God doesn't exist. In the current philosophical climate, it's believed that this amounts to a contradiction and ergo, one of the two has to be false.
If, on the other hand, we treat both theism and atheism as true but from different points of view (2D shadows, square & circle) we could use them to home in on the higher truth (3D cylinder) that's part of a higher reality.
The point to all this being contradictions (square circles like atheism vs theism, physicalism vs nonphysicalism, etc.) are actually not contradictions. They're just different sides (anekantavada, many-sidedness, Jainism) of the same greater truth that resides in a world the next level up so to speak.
Addendum 2
The idea that I want to convey here has illustrious origins in Jainism and it's called anekantavada (not-one-sidedness or many-sidedness) aka perspectivism in the western world. Enough said!
If we get the right angle for the light shining on the 3D cyclinder - my experiments show that this sweet spot lies between the angle of light that casts a square shadow and the angle of light that casts a circular shadow - what we'll get is the correct shadow/projection of the 3D cylinder - two ellipses (the two circles of the 3D cylinder) with two parallel lines joining the circumferences of these circles and this is the true 2D shadow/projection of a 3D cylinder. Let's call this true 2D shadow/projection of a 3D cylinder C.
What's interesting is C is produced when the angle of light shining on the 3D cylinder is in the middle between that angle which produces a square shadow and the other angle that produces a circular shadow. As some say,
There are two sides to every story and somewhere in the middle lies the truth. — Some guy
This, I suppose, is the Buddha's madhyamaka/the middle path.
It appears there is such a thing as right perspective? the point of view that reveals the truth, the real truth, the whole truth! -
 javi2541997
7.1ktwo parts of which describe qualities that cannot both exist in the same thing at the same time. — Citizendium
javi2541997
7.1ktwo parts of which describe qualities that cannot both exist in the same thing at the same time. — Citizendium
:up: :100:
Law Of Noncontradiction! — TheMadFool
Thanks for sharing. Another interesting article to read about.
This OP reminds me when we debated about Gödel's mathematics principles. Human mind can be sometimes so spectacular. As you shared with us in the first paragraph, we can develop in our mind a completely contradiction: Square circle.
Metaphysics can allow us to go further than our possibilities. It is the Great act of dreaming in "practice." This is the main reason why we can create or build aspects that previously we can think they are "impossible". Later on, giving a chance to our knowledge, we can improve the reality and get all what we were dreaming about.
(example: apart from 3D images, appoint a journey to the moon or Mars. This project looked impossible back in the day...)
I guess more important than a paradox (or whatever we can call this metaphysical issue :D) it is about how our mind can do excellent things. Thus, go further than reality could be. -
 litewave
894Consider now a 3D object, a right cylinder with height 4 units and diameter 4 units. Depending on the angle of the light you shine on it, the shape of its shadow will change. — TheMadFool
litewave
894Consider now a 3D object, a right cylinder with height 4 units and diameter 4 units. Depending on the angle of the light you shine on it, the shape of its shadow will change. — TheMadFool
A contradictory proposition affirms that something has and does not have the same property. But a proposition that affirms that something looks like a circle from one perspective and does not look like a circle from another perspective is not a contradiction because the property of "looking like a circle from one perspective" is not the same property as "looking like a circle from another perspective".
Sometimes it is said for emphasis that a contradictory proposition affirms that something has and does not have the same property at the same time, and/or in the same sense, but these additions can be seen as already included in the meaning of the phrase "same property". -
 jgill
4kA circle and a square are topologically equivalent. In a sense they are the same collection of points, deformed continuously from one to the other. So, in a sense there is a shape-changing entity having many forms. Well, that's a philosophical way of looking at it. :roll:
jgill
4kA circle and a square are topologically equivalent. In a sense they are the same collection of points, deformed continuously from one to the other. So, in a sense there is a shape-changing entity having many forms. Well, that's a philosophical way of looking at it. :roll: -
TheMadFool
13.8kA contradictory proposition affirms that something has and does not have the same property. But a proposition that affirms that something looks like a circle from one perspective and does not look like a circle from another perspective is not a contradiction because the property of "looking like a circle from one perspective" is not the same property as "looking like a circle from another perspective".
Sometimes it is said for emphasis that a contradictory proposition affirms that something has and does not have the same property at the same time, and/or in the same sense, but these additions can be seen as already included in the meaning of the phrase "same property". — litewave
There's no contradiction here.
↪litewave Yep. Nothing to see here. — Banno
Please read my addendum to the OP. -
TheMadFool
13.8kThus, go further than reality could be. — javi2541997
:up: I suspect people are bored with reality and what it puts on the table. They thirst for more and if you look at extreme sports and how popular they are, I'd say people are willing to pay the ultimate price just to get that adrenaline rush. If you like bungee jumping, why not just cut to the chase and go skydiving! That's how some of us seem to approach the issue. I'm all for it despite the many funerals that have been/are/will be held on this account. -
 litewave
894Addendum
litewave
894Addendum
If a contradiction is being sought for, it's this: As litewave pointed out, some of us will observe T' as a square (S) and others will observe T' as as a circle (~S). Both parties are right: Square Circle. — TheMadFool
Square circle as a genuinely contradictory object would look like a square and like a circle from the same perspective (and at the same time and under all other same circumstances). Such an object cannot exist. -
TheMadFool
13.8kSquare circle as a genuinely contradictory object would look like a square and like a circle from the same perspective (and at the same time and under all other same circumstances). Such an object cannot exist — litewave
Indeed, how right you are. It is the same perspective - a 2D perspective of a 3D proposition. -
 Banno
30.1kIf a contradiction is being sought for, it's this: As litewave pointed out, some of us will observe T' as a square (S) and others will observe T' as as a circle (~S). Both parties are right: Square Circle. — TheMadFool
Banno
30.1kIf a contradiction is being sought for, it's this: As litewave pointed out, some of us will observe T' as a square (S) and others will observe T' as as a circle (~S). Both parties are right: Square Circle. — TheMadFool
This is what leads me away from reading your posts.
A square circle would be a regular polygon with four sides, the perimeter of which is equidistant from a given point on the same plane.
Draw me one of those. -
 fishfry
3.4kSquare circle as a genuinely contradictory object would look like a square and like a circle from the same perspective (and at the same time and under all other same circumstances). Such an object cannot exist — litewave
fishfry
3.4kSquare circle as a genuinely contradictory object would look like a square and like a circle from the same perspective (and at the same time and under all other same circumstances). Such an object cannot exist — litewave
In the taxicab metric the unit circle is a square. There's a picture of a square circle on that page. A circle is the set of points equidistant from a given point. If you choose your distance function appropriately, a circle can be a square.
Note that this is very different than an unmarried bachelor. A bachelor by definition is a male who is not married. so that a married bachelor is indeed a contradiction.
But a circle and a square are NOT defined as each other's opposites, nor are they mutually exclusive at all. People should stop using square circles as an example of a contradiction, because in fact there are square circles.
Note that if you define the distance between two points to be the sum of the horizontal and vertical distance between them, then the distance of each red point from the blue point is the same in each case, and that these are therefore square circles. (This is the Wiki image).
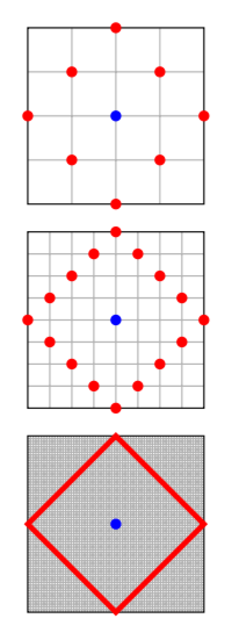
A square circle would be a regular polygon with four sides, the perimeter of which is equidistant from a given point on the same plane.
Draw me one of those. — Banno
Done. It all depends on how you define distance. Standard Euclidean distance (square root of the sum of the squares of the respective differences of the coordinates) is only one way of defining distance. Even in physics, Euclidean distance is only a special case of a more general way of defining distance. -
TheMadFool
13.8kThis is what leads me away from reading your posts.
A square circle would be a regular polygon with four sides, the perimeter of which is equidistant from a given point on the same plane.
Draw me one of those. — Banno
Many thanks for the challenge. The point I' making is that there are only apparent contradictions, not real ones. If given a contradiction, p & ~p, we can very easily extricate ourselves from this rather painful predicament by saying p from one point of view and ~p from another (apparent contradiction) and not from the same point of view (real contradiction).
Can you go through the addendum I appended to the OP. There are some critical changes. -
TheMadFool
13.8kSquare circle as a genuinely contradictory object would look like a square and like a circle from the same perspective (and at the same time and under all other same circumstances). Such an object cannot exist. — litewave
I did some reading up and what my OP is about matches what Jains had to say about truth 2,500 years ago (yeah! that's how old my idea is). Jainism has a concept called Anekantavada (many-sidedness) which your posts echo. According to anekantavada, contradictions can be, in a sense, resolved, with the help of perspectivism. Given a contradiction p & ~p, we can say that p from one angle and ~p from another angle and not p & ~p from the same angle.
Thanks a million!
As for the claim that a square circle is a contradiction, all I can say is it's a square from one standpoint and a circle from another standpoint (like a 3D cylinder) but not both a square and a circle from the same standpoint. -
 litewave
894But a circle and a square are NOT defined as each other's opposites, nor are they mutually exclusive at all. — fishfry
litewave
894But a circle and a square are NOT defined as each other's opposites, nor are they mutually exclusive at all. — fishfry
In Euclidean space they are mutually exclusive and I tacitly assumed this kind of space. Thanks for pointing out that there are also spaces with such a metric that a circle looks like a square. -
TheMadFool
13.8kBut a circle and a square are NOT defined as each other's opposites, nor are they mutually exclusive at all. People should stop using square circles as an example of a contradiction, because in fact there are square circles. — fishfry
Interesting post. For once I understood some math, weird math to be precise.
However, I believe that squares and circles are mutually exclucive unless you want to demonstrate the existence of a square circle and mind you, not by tweaking definitions as you've done with the so-called taxicab metric.
I'm glad that you brought up the matter of mutual exclusivity vis-à-vis contradictions. There's another side to the story of a proposition p and its negation ~p that needs to be taken into consideration viz. p and ~p are also, in addition to being mutually exclusive, also jointly exhaustive i.e. between p and ~p, all there is must be either p or ~p, the residue being the null set { }.
Why I felt comfortable with a square circle as a contradiction is because a circle is not a square and thus I assigned squares to S and circles to ~S. S and ~S and voila, we have a contradiction (mutually exclusive and jointly exhaustive). Too, a contradiction is defined as false in all possible worlds and a square circle is also false in all possible worlds given we stick to standard definitions. -
TheMadFool
13.8kIn Euclidean space they are mutually exclusive and I tacitly assumed this kind of space. — litewave
In what kind of space are there square circles? I'm curious. -
 litewave
894The point I' making is that there are only apparent contradictions, not real ones — TheMadFool
litewave
894The point I' making is that there are only apparent contradictions, not real ones — TheMadFool
A genuinely contradictory object cannot exist so any object in reality can be only seemingly contradictory. -
TheMadFool
13.8kA genuinely contradictory object cannot exist so any object in reality can be only seemingly contradictory. — litewave
There are no genuine contradictions. That's the law :point: The Law of Noncontradiction ~(p &~p), only apparent contradictions that can be resolved with anekantavada (many-sidedness/perspectivism).
However, apparent contradictions could be shadows of higher truths in higher realities from different perspectives, projected onto our world. -
 litewave
894In what kind of space are there square circles? I'm curious. — TheMadFool
litewave
894In what kind of space are there square circles? I'm curious. — TheMadFool
In the space with taxicab metric that fishfry mentioned. You may object that that is actually not a circle but he did use the standard definition of a circle: a set of points with a fixed distance from some point. -
 litewave
894There are no genuine contradictions. That's the law :point: The Law of Noncontradiction ~(p &~p), only apparent contradictions that can be resolved with anekantavada (many-sidedness/perspectivism). — TheMadFool
litewave
894There are no genuine contradictions. That's the law :point: The Law of Noncontradiction ~(p &~p), only apparent contradictions that can be resolved with anekantavada (many-sidedness/perspectivism). — TheMadFool
You can still formulate a genuinely contradictory proposition by insisting on the same perspective but such a proposition would not correspond to any object in reality. -
TheMadFool
13.8kIn the space with taxicab metric that fishfry mentioned. You may object that that is actually not a circle but he did use the standard definition of a circle: a set of points with a fixed distance from some point. — litewave
He messed around with the definition of distance - the way a taxicab moves around a city, a well-planned city with all roads at right angles to each other. -
TheMadFool
13.8kYou can still formulate a genuinely contradictory proposition by insisting on the same perspective but such a proposition would not correspond to any object in reality — litewave
That's wordplay. "genuinely contradictory proposition" and "such a proposition would not correspond to any object in reality" is a contradiction. Impossible! Nevertheless, from different viewpoints both are true. -
TheMadFool
13.8kEven in physics, Euclidean distance is only a special case of a more general way of defining distance. — fishfry
Didn't know that! :up: There's more than one way to skin a cat although it escapes me why anyone would want to do that. -
 litewave
894That's wordplay. — TheMadFool
litewave
894That's wordplay. — TheMadFool
Insistence on the same perspective was part of the meaning of a contradiction already in ancient Greece:
Aristotle's law of noncontradiction states that "It is impossible that the same thing can at the same time both belong and not belong to the same object and in the same respect."
https://en.wikipedia.org/wiki/Contradiction
(emphasis mine) -
 javi2541997
7.1kIt is impossible that the same thing can at the same time both belong and not belong to the same object and in the same respect." — litewave
javi2541997
7.1kIt is impossible that the same thing can at the same time both belong and not belong to the same object and in the same respect." — litewave
Aristotle meant to the object itself not the act of belonging to another.
The “same thing” that belongs must be one and the same thing and it must be the actual thing and not merely its linguistic expression. For example, it is possible for someone to be a pitcher and not a pitcher where “pitcher” in the first instance refers to a baseball player and in the second to a jug that can hold beer
Three Versions of the Principle of Non-Contradiction -
 litewave
894Aristotle meant to the object itself not the act of belonging to another.
litewave
894Aristotle meant to the object itself not the act of belonging to another.
The “same thing” that belongs must be one and the same thing and it must be the actual thing and not merely its linguistic expression. For example, it is possible for someone to be a pitcher and not a pitcher where “pitcher” in the first instance refers to a baseball player and in the second to a jug that can hold beer — javi2541997
I don't see that the article attributes the phrase "in the same respect" to the object. It seems more likely that "in the same respect" refers to the act of belonging. -
TheMadFool
13.8kInsistence on the same perspective was part of the meaning of a contradiction already in ancient Greece:
Aristotle's law of noncontradiction states that "It is impossible that the same thing can at the same time both belong and not belong to the same object and in the same respect."
https://en.wikipedia.org/wiki/Contradiction
(emphasis mine) — litewave
We're talking past each other. I agree with you that real contradictions are impossible. If someone claims a contradiction as real, say p & ~p, all we have to do to resolve it is to say p from one angle, ~p from another angle but not the case that p & ~p from the same angle. The p & ~p was only an apparent contradiction. -
TheMadFool
13.8kBTW, for those interested, in spherical geometry there are square circles but no contradiction because their definitions have been adapted to the sphere's surface. -
 javi2541997
7.1kI don't see that the article attributes the phrase "in the same respect" to the object. — litewave
javi2541997
7.1kI don't see that the article attributes the phrase "in the same respect" to the object. — litewave
Literally the article says:
An object can be potentially F and potentially not F, but it cannot be actually F and actually not F at the same time. -
 baker
5.9kThe point to all this being contradictions (square circles like atheism vs theism, physicalism vs nonphysicalism, etc.) are actually not contradictions. They're just different sides (anekantavada, many-sidedness, Jainism) of the same greater truth that resides in a world the next level up so to speak. — TheMadFool
baker
5.9kThe point to all this being contradictions (square circles like atheism vs theism, physicalism vs nonphysicalism, etc.) are actually not contradictions. They're just different sides (anekantavada, many-sidedness, Jainism) of the same greater truth that resides in a world the next level up so to speak. — TheMadFool
Sure. But what is the use of this? It's not as if understanding that things look differently from different perspectives is going to bring about world peace.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum





