-
 Pfhorrest
4.6kIn a previous thread, I proposed the use of a set of logical functions to indicate the kind of speech-act being made, especially distinguishing the direction-of-fit aspect of it, so that that part of an expression can be separated from the propositional content of the speech-act, the idea that the speech-act is about. This is primarily because all of the rest of logic is about the relationships between those ideas alone, independent of whatever we might be communicating about some attitudes toward those ideas.
Pfhorrest
4.6kIn a previous thread, I proposed the use of a set of logical functions to indicate the kind of speech-act being made, especially distinguishing the direction-of-fit aspect of it, so that that part of an expression can be separated from the propositional content of the speech-act, the idea that the speech-act is about. This is primarily because all of the rest of logic is about the relationships between those ideas alone, independent of whatever we might be communicating about some attitudes toward those ideas.
A classic example of a formal logical inference is that from the propositions "all men are mortal" and "Socrates is a man" we can logically infer the proposition "Socrates is mortal". But, I hold, we could equally well infer from the propositions "all men ought to be mortal" and "Socrates ought to be a man" that "Socrates ought to be mortal". I say that it is really just the ideas of "all men being mortal" and "Socrates being a man" that entail the idea of "Socrates being mortal", and whether we hold descriptive, mind-to-fit-world attitudes about those ideas, or prescriptive, world-to-fit-mind attitudes about them, whether we're impressing or expressing those attitudes, even whether we're making statements or asking questions about them, does not affect the logical relations between the ideas at all.
So I propose that rather than treating a statement like "All men are mortal" as one proposition and a statement like "All men ought to be mortal" as another, completely unrelated proposition, we instead take the idea that they have in common, "all men being mortal", and wrap that in a function that conveys what we wish to communicate about some attitude toward that idea. For example we might write there-is(all men being mortal) to mean "all men are mortal", and be-there(all men being mortal) to mean "all men ought to be mortal"; and generally, write there-is(S) and be-there(S) for the equivalent descriptive and prescriptive statements about the idea of some state of affairs S, whatever S is. We might wish to use shorter names for the functions, like simply is() and be(), or some other names entirely; I am merely using the indicative and imperative moods of the copula verb "to be" to capture the descriptive and prescriptive natures of the respective functions.
Show Unimportant DetailsThese as I've written them so far are both implicitly statements and impressions (see previous thread for details on those), but we could also use a whole variety of similar functions to differentiate expressions from impressions and questions from statements, for example prepending an exclamation mark or question mark to differentiate statements from questions, as in !there-is() and ?there-is(), and prepending, say, a right-bracket for impression or a left-bracket for expression, as in !>there-is() and !<there-is(). We can think of these punctuation marks themselves as unary functions for which we are simply not writing the parentheses, giving us a total of six functions, three pairs of functions:
!() and ?()
>() and <()
is() and be()
or a total of eight possible combinations thereof:
!>is() ("there is..." something)
!>be() ("there should be..." something)
!<is() ("I think there is..." something)
!<be() ("I think there should be..." something)
?>is() ("is there...?" something)
?>be() ("should there be...?" something)
?<is() ("I wonder if there is..." something)
?<be() ("I wonder if there should be..." something)
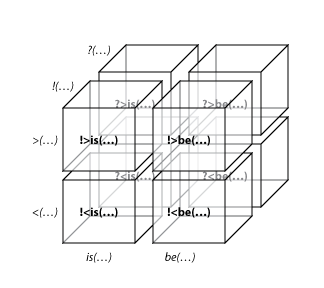
...to indicate the various different things we might wish to communicate about different attitudes toward the same, single, idea. All of the rest of logic can then deal entirely with such ideas, and the relations between them, without concerning itself with what anyone might be communicating about which of the various possible attitudes toward them. I call these kinds of functions "mood" functions, after their similarity to the concept of linguistics moods, such as the indicative and the imperative.
The use of these mood functions also facilitates something superficially resembling the motivations for non-classical types of logic such as paraconsistent logics and intuitionist logics, without actually abandoning the principle that differentiates classical logic from them: the principle of bivalence. The principle of bivalence is the principle that every statement must be assigned exactly one of two truth values, "true" or "false", no more and no less. Intuitionist logics allow for statements to be assigned neither of those truth values, while paraconsistent logics allow for statements to be assigned both of them at the same time.
With these mood functions, similar things can be constructed without actually violating the principle of bivalance, because there is nothing strictly logically prohibiting it being the case that neither is(P) nor is(not-P), if for example P were some kind of descriptively meaningless statement; it is merely necessary, to preserve bivalance, that either is(P) or not(is(P)), but not(is(P)) doesn't have to entail that is(not-P). Similarly, there is nothing strictly prohibiting it being the case that be(P) and be(not-P), if for example there were some morally intractable situation where both P and not-P were required, and so any outcome was unacceptable; it is merely necessary, to preserve bivalence, that either be(P) or not(be(P)), but not(be(P)) doesn't have to entail be(not-P).
Fleshing out the philosophical implications of things like descriptively meaningless claims and morally intractable situations is a topic for further discussion. But in any case a logic of this form is in principle capable of discussing things that are, in a loose sense, "both true and false" or "neither true nor false", without technically violating the principle of bivalence. -
 EnPassant
716I proposed the use of a set of logical functions to indicate the kind of speech-act being made, especially distinguishing the direction-of-fit aspect of it, so that that part of an expression can be separated from the propositional content of the speech-act, the idea that the speech-act is about. This is primarily because all of the rest of logic is about the relationships between those ideas alone, independent of whatever we might be communicating about some attitudes toward those ideas. — Pfhorrest
EnPassant
716I proposed the use of a set of logical functions to indicate the kind of speech-act being made, especially distinguishing the direction-of-fit aspect of it, so that that part of an expression can be separated from the propositional content of the speech-act, the idea that the speech-act is about. This is primarily because all of the rest of logic is about the relationships between those ideas alone, independent of whatever we might be communicating about some attitudes toward those ideas. — Pfhorrest
Language is not, generally speaking, as rigorous as logic. One should not confuse the two. As you say, it is the logical relationship between ideas that count, not the subtle variations in how we convey ideas by language. -
 Pfhorrest
4.6kLanguage is not, generally speaking, as rigorous as logic. — EnPassant
Pfhorrest
4.6kLanguage is not, generally speaking, as rigorous as logic. — EnPassant
Logic is a subset of language, but yes, natural language is not usually as rigorous. The reason for inventing systems of logic is to have a more rigorous way of clarifying what we say and the relationships between different things we say.
This proposal is aimed primarily at clarifying the relationship between sentences that are saying different things about the same state of affairs. But it also, incidentally and interestingly, has implications on the things that non-classical logics are aiming to do, without abandoning the principle of bivalence like they do. -
 Pfhorrest
4.6kI forgot to include something else in the OP:
Pfhorrest
4.6kI forgot to include something else in the OP:
Traditionally, both alethic and deontic modal logics write their core functions, either necessity and possibility or obligation and permission, with the same □ and ◇ operators, their meaning distinguished only by the surrounding context. But with the mood operators described above, there is no need for that context, because once we have abstracted the descriptiveness or prescriptiveness of statements away into those mood operators, we are dealing only with the raw idea of whatever state of affairs being or not-being in some variety of contexts.
The usual semantics given to the alethic modal operators is that of "possible worlds": for something to be necessary is for it to be true in all possible worlds, for it to be possible is for it to be true in some possible worlds, for it to be impossible is for it to be true in no possible worlds, and for it to be contingent is for it to be true in not all possible worlds. If we take those □ and ◇ operators to mean not specifically anything about alethic necessity or possibility, nor deontic obligation or permission, but instead as just representing the idea of whatever they are applied to being the case in either all or merely some possible worlds, then when we wrap our descriptive or prescriptive mood functions around them, we automatically get an alethic or deontic logic, both with all the same internal structure.
The descriptive mood function asserts that whatever idea being the case in whatever set of possible worlds is true, yielding necessity, possibility, etc; while the prescriptive mood function asserts that it is good, yielding obligation, permission, etc. For something to be obligatory is for the idea of it being the case in all possible worlds to be good; and for something to be permissible is for the idea of it being the case in some possible worlds to be good. For something to be obligatory is for it to be good for that thing to be necessary; and for something to be permissible is for it to be good for that thing to be possible.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- If I were aware of the entire list of logical fallacies, would I be exempt from making wrong/bad...
- Can unproven or hard to debunk logical chain create or support religion?
- Logical positivism was right, with respect to an ideal logical language.
- The differences/similarities between analytic, a priori, logical necessity, and absolute certainty
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum

