It is already well-known in contemporary logic that the ordinary truth-functions like "and", "or", "if-then", etc, can be readily converted between each other; for example, conjunction ("and") and disjunction ("or") are De Morgan duals, where the negation of a conjunction ("not (A and B)") is equivalent to the disjunction of negations ("not-A or not-B"), and conversely the negation of a disjunction ("not (A or B)") is equivalent to the conjunction of negations ("not-A and not-B").

Implication ("if A then B" or "A only if B") in turn is equivalent to a certain kind of conjunction ("not (A and not-B)") which is likewise equivalent to another kind of disjunction ("not-A or B"); the reverse of implication ("A if B"), which I like to call "explication", is likewise equivalent to that conjunction and that disjunction with the negations of their terms likewise reversed ("not(not-A and B)" or "A or not-B"). Bi-implication ("A if and only if B"), which I like to call "complication" (meaning "bending together", as "implication" means "bending into" and "explication" means "bending out of"), is of course the conjunction of both implication and explication; and what's usually called "exclusive disjunction" ("A xor B"), which I prefer to call "displication" (meaning "bending apart"), is the negation of that.

There are still other, much less used, logical functions for saying which if either of two things must or must not be the case together for the entire state of affairs thus encoded to be the case, but the two most important ones are usually called "alternative denial" ("A nand B") and "joint denial" ("A nor B"), though I prefer to call them "disnegation" (meaning "negating apart") and "conegation" (meaning "negating together"). These two functions are important because either one of them can serve as a sole sufficient operator to build any of these functions I have just described, and the equally-many lesser-used ones I haven't even bothered to describe here.

I made a nifty little chart showing the truth-tables for every possible boolean truth function, with symbols mostly taken from standard logics, with a few slight modifications for symmetry, and my new name suggestions as listed above:



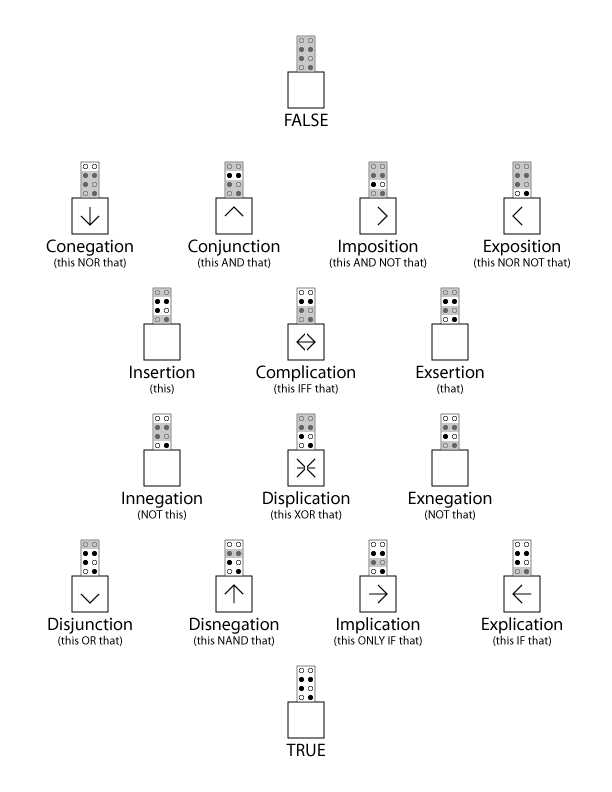
But besides the few new names and symbols above, my main proposal for improvement in this aspect of logic is the introduction of yet another single, broader function that can serve in place of all of these other functions. (Like I've recently proposed for modal functions, quantification functions, and predication functions).

I call it the "junction" function, after functions like conjunction and disjunction, but I write it of(), because it takes two arguments, a number and a set, and returns that number of members of that set, and so can be used to mean things like "none of...", "some of...", "all of...", etc. And more broadly, specific numbers, like "two of..." or "five of..." or, with some extra logic in the first argument, things like "between three and seven of...".

But if the number in the first argument is zero, it returns no members of that set, and so is equivalent to the conegation, or joint denial, of all members of that set. That can then be used to construct any of the other functions just like a traditional joint denial function can:

- The conegation of a single item is just that item's negation, so this serves straightforwardly in place of "not".

- The negation of a conegation of several things is equivalent to the disjunction of those several things, i.e. "not (neither A nor B nor C ...)" just means "A or B or C ...", so we have replicated the functionality of "or".

- The conegation of the negations of several things is equivalent to the conjunction of those several things, i.e. "neither not-A nor not-B nor not-C ..." just means "A and B and C ...", so we have replicated the functionality of "and".

- And the negation of such a conjunction is a disnegation, or alternative denial, i.e. "not (neither not-A nor not-B nor not-C ...)" just means "A nand B nand C ...", so we have replicated the functionality of "nand".

And so on with all those we can replicate the functionality of implication, explication, complication, displication, and the rest of the truth-functions, with this one single function.