-
 Leontiskos
5.6kIncorrect. — Michael
Leontiskos
5.6kIncorrect. — Michael
You should have read beyond the first few sentences of that post. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
I think it depends on what "logical" is supposed to mean.
I would maybe think of these issues as somewhat analagous to software bugs. Video games are a good example. Some classic games that are very well received are also very buggy. You can break them, either making them trivial or else just causing crashes or all sorts of bizarre behavior.
The game still serves its purpose. It does what we want. We just know, "don't do that or you will break it." And if "that" is not something we're likely to do by accident, it really isn't a huge problem. Yet we still might want to patch the bug, but this can also be done in ways that are straightforward and "make sense," or in ways that just seem like ad hoc papering over, just like you can do good body work on a car and restore it, or just pull out the Bondo and patch it.
But when it comes to "correct reasoning," we are talking about something essential to human flourishing, freedom, and even the rise and fall of civilization. So probably want to get to the bottom of any bugs.
Explosion seems like a bug. Suppose we think common paradoxes of self-reference involve situations where statements are really both true and false. Yet even if this is so, we will likely think that this does not constitute a good reason to think that everything is both true and false. -
 Leontiskos
5.6kWe just know, "don't do that or you will break it." — Count Timothy von Icarus
Leontiskos
5.6kWe just know, "don't do that or you will break it." — Count Timothy von Icarus
Yep, and this goes to @Srap Tasmaner's notion of "degenerate cases" (of, say, the material conditional). If one does not see logic as teleological, then there can be no degenerate or non-degenerate cases.
Note too that formal logic is supposed to involve no rules that require interpretation. But once we introduce "degenerate cases," we have introduced a rule or norm of logic that requires interpretation. This is why formalists dislike the notion of degenerate cases. -
 Srap Tasmaner
5.2kSrap Tasmaner's notion of "degenerate cases" — Leontiskos
Srap Tasmaner
5.2kSrap Tasmaner's notion of "degenerate cases" — Leontiskos
For the record, it's not my notion, it's what mathematicians call them. A triangle with interior angles of 180/0/0 would be a degenerate triangle. It allows you to say that any three points in a plane determine a triangle instead of saying that any three non-colinear points do. Mathematicians are generally pleased when they don't have to make special rules to cover edge cases. -
 jgill
4kA triangle with interior angles of 180/0/0 would be a degenerate triangle. It allows you to say that any three points in a plane determine a triangle instead of saying that any three non-colinear points do. Mathematicians are generally pleased when they don't have to make special rules to cover edge cases. — Srap Tasmaner
jgill
4kA triangle with interior angles of 180/0/0 would be a degenerate triangle. It allows you to say that any three points in a plane determine a triangle instead of saying that any three non-colinear points do. Mathematicians are generally pleased when they don't have to make special rules to cover edge cases. — Srap Tasmaner
Hmmm . . . so the common triangle is a non-degenerate triangle. I doubt I ever used the expression, "degenerate". But I see it's popular on Wikipedia.
However, I've always liked the expression "indifferent fixed point". Rather than "neutral fixed point".
Who would have thought the ridiculous expression A -> -A would go for one K posts? -
 NotAristotle
587You're right that the conclusion utilizes modus tollens, but here is the way that modus ponens is operating metalogically:
NotAristotle
587You're right that the conclusion utilizes modus tollens, but here is the way that modus ponens is operating metalogically:
(1 ^ 2) → 3
(1 ^ 2)
∴ 3 — Leontiskos
I was reviewing this thread and it occurs to me that I disagree with the contention that the argument I stated:
1. If MP could be false, then RAA could be false.
2. But RAA is not false.
3. Therefore neither is MP. — NotAristotle
is metalogically an MP argument. In fact, I think the argument is metalogically neither MP nor simply making use of a material conditional. Instead, I think it is independently an MT argument structurally and does not collapse into MP. If it were a conditional metalogically, it would have to be a degenerative case. Instead of:
1 and 2 therefore 3.
1 and 2.
Therefore, 3.
The initial argument I forwarded would, I think, be more like:
1 and 2 then not 1.
1 and 2.
Therefore not 1.
But, whether such an argument is valid, an argument of this form surely is not convincing, and is therefore a bad argument. And so, if I am correct that the initial argument concerning RAA, MT, and MP is a good argument, then it must not be a degenerative instance of a conditional and must instead be a true to form example of MT structurally and irreducible to MP. -
 Srap Tasmaner
5.2k1 and 2 then not 1.
Srap Tasmaner
5.2k1 and 2 then not 1.
1 and 2.
Therefore not 1. — NotAristotle
That's modus ponens. -
 NotAristotle
587I thought we were differentiating between a use of the material conditional versus modus ponens as a mode of discursive thought. In what world is "1 and 2 therefore not 1. 1 and 2. Therefore, not 1." a sensible or logical maneuver? It most certainly is not modus ponens so understood.
NotAristotle
587I thought we were differentiating between a use of the material conditional versus modus ponens as a mode of discursive thought. In what world is "1 and 2 therefore not 1. 1 and 2. Therefore, not 1." a sensible or logical maneuver? It most certainly is not modus ponens so understood. -
 Srap Tasmaner
5.2ka mode of discursive thought — NotAristotle
Srap Tasmaner
5.2ka mode of discursive thought — NotAristotle
I don't know what that is. I was just referring to the form. From ~1 you can next derive ~(1 & 2), so now you have a contradiction.
I don't remember what the point of all this was supposed to be. -
 NotAristotle
587My point in these last few comments is just that MT is not an instance of MP metalogically. I think it would be more accurate to say that formally, the argument you just stated makes use of a material conditional that when applied to natural language will turn out to not make any sense or be an instance of bad argumentation.
NotAristotle
587My point in these last few comments is just that MT is not an instance of MP metalogically. I think it would be more accurate to say that formally, the argument you just stated makes use of a material conditional that when applied to natural language will turn out to not make any sense or be an instance of bad argumentation. -
 NotAristotle
587Not that it is an instance of MP, which is a logical "move," not a merely formal property.
NotAristotle
587Not that it is an instance of MP, which is a logical "move," not a merely formal property. -
 Srap Tasmaner
5.2kMP, which is a logical "move," not a merely formal property — NotAristotle
Srap Tasmaner
5.2kMP, which is a logical "move," not a merely formal property — NotAristotle
It's usually taken as an inference rule, if that's what you mean.
MT is not an instance of MP — NotAristotle
Given MP as an inference rule, can you derive MT? That is, is MT a theorem? -
 NotAristotle
587Good questions. I would tend to think MT is another inference rule that cannot be "derived" from a different inference rule like MP; that is, MT is not a theorem that can be derived from MP. At that point I think we are left to our intuitions about what inference rules to assent to. I think MP, MT, and RAA are all equally intuitive and so they all fall or stand together; that's the idea behind the coherence argument I forwarded earlier in the thread with RAA, MP, and MT. In effect, you can prove, or argue for, MP based on affirming RAA and MT. Or, you could instead argue for MT based on affirming RAA and MP.
NotAristotle
587Good questions. I would tend to think MT is another inference rule that cannot be "derived" from a different inference rule like MP; that is, MT is not a theorem that can be derived from MP. At that point I think we are left to our intuitions about what inference rules to assent to. I think MP, MT, and RAA are all equally intuitive and so they all fall or stand together; that's the idea behind the coherence argument I forwarded earlier in the thread with RAA, MP, and MT. In effect, you can prove, or argue for, MP based on affirming RAA and MT. Or, you could instead argue for MT based on affirming RAA and MP. -
 Michael
16.6kIn what world is "1 and 2 therefore not 1. 1 and 2. Therefore, not 1." a sensible or logical maneuver? It most certainly is not modus ponens so understood. — NotAristotle
Michael
16.6kIn what world is "1 and 2 therefore not 1. 1 and 2. Therefore, not 1." a sensible or logical maneuver? It most certainly is not modus ponens so understood. — NotAristotle
The bottom line shows modus ponens. It doesn't matter what A and B mean:
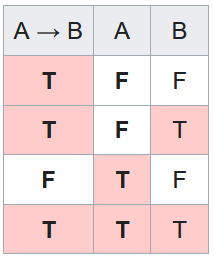
Now replace B with ¬A. Only one line has both A → ¬A and A true, and on that line ¬A is also true. That's all it means for the argument to be valid.
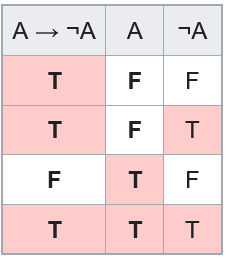
However, two of the lines are removed by the laws of excluded middle (the top) and non-contradiction (the bottom)
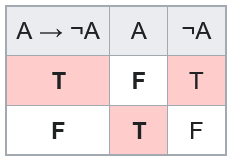
That gives us:
A → ¬A
∴ ¬A
Or
A
∴ ¬(A → ¬A)
So the argument is unsound. -
 Leontiskos
5.6kMy point in these last few comments is just that MT is not an instance of MP metalogically. — NotAristotle
Leontiskos
5.6kMy point in these last few comments is just that MT is not an instance of MP metalogically. — NotAristotle
I continue to think that modus ponens is always operating metalogically:
Yes, but I think that all arguments are, structurally, modus ponens. This goes back to the earlier point about whether all arguments are modus ponens, or whether all arguments utilize a material conditional. Tones is claiming that the metalogical inference uses a material conditional, and is not merely a modus ponens, and that this is why he thinks inconsistent premises automatically* make an argument valid [whereas I think a mere modus ponens is at play]. — Leontiskos
The initial argument I forwarded... — NotAristotle
Which was this:
1. If MP could be false, then RAA could be false.
2. But RAA is not false.
3. Therefore neither is MP. — NotAristotle
The initial argument I forwarded would, I think, be more like:
[If] 1 and 2 then not 1.
1 and 2.
Therefore not 1. — NotAristotle
The most obvious problem is that you seem to be misrepresenting your own argument. Your argument is a modus tollens that metalogically comes to this modus ponens:
- If 1 and 2, then not [antecedent of 1]
- 1 and 2
- Therefore, not [antecedent of 1]
You are mixing up the antecedent of 1 with 1 itself. But I think my phrasing is preferable since there really is a 3 in the object-level argument, namely the conclusion. The conclusion is not reducible to the premises, and neither is it "not 1." Once we recognize that the conclusion, namely 3, is the same as "not [antecedent of 1]," we see that the two construals are identical, and that both utilize modus ponens.
I still agree with what I said about the metalogical question .
* Note that we could generalize the form of this modus ponens representation of modus tollens:
- If [conditional] and [negation of conditional's consequent], then [negation of conditional's antecedent]
- [Conditional] and [negation of conditional's consequent]
- Therefore, [negation of conditional's antecedent]
(Edit: for the root issue, see my post <here>. If someone like Tones thinks RAA equally entails two completely different conclusions and makes no recourse to explosion, then I think it is obvious that what I have said about RAA is correct. Namely: The RAA inference is not as metalogically secure as the modus ponens inference, and the introduction of something which can be construed as semantically equivalent to Falsum helps show this.) -
 NotAristotle
587The most obvious problem is that you seem to be misrepresenting your own argument. — Leontiskos
NotAristotle
587The most obvious problem is that you seem to be misrepresenting your own argument. — Leontiskos
I would not say I misrepresented my own argument, I would say I miswrote your representation of my argument.
Would you agree that your representation of my argument:
(1 ^ 2) → 3
(1 ^ 2)
∴ 3 — Leontiskos
could also be written as follows...
A. not-3 then not-2. And 2. Then 3.
B. not-3 then not-2. And 2.
C. Therefore 3.
If you agree that this is accurate, it seems to me that we can see that the argument will be correct because of modus tollens. In particular, we can see that the "A" premise is already agreeable because of modus tollens. If you had instead forwarded premise "A" to be "not-3 then not-2. And 2. Then not-3...," then it's clear that the conditional would not be doing any of the work. The modus tollens makes all the difference does it not? It confirms the truth of the conditional in premise "A" that serves as the basis for the argument's modus ponens. In other words, premise "A" is true "a priori" (if I can use that term here) because of the modus tollens logic, and the truth of that premise gives the basis for the rest of the argument. Premise "B" becomes the only questionable premise. Given it's truth, the argument necessarily works because premise "A" thanks to modus tollens, cannot be questioned.
So maybe you are right that any argument can be written metalogically as a modus ponens, but I think it cannot be so written without the logical inferences that the argument require, in this case a modus tollens is necessary to the argument and cannot be written off as being a hidden modus ponens.
What do you think? -
 Leontiskos
5.6kI would not say I misrepresented my own argument, I would say I miswrote your representation of my argument. — NotAristotle
Leontiskos
5.6kI would not say I misrepresented my own argument, I would say I miswrote your representation of my argument. — NotAristotle
Here is your argument:
1. If MP could be false, then RAA could be false.
2. But RAA is not false.
3. Therefore neither is MP. — NotAristotle
Here is my construal:
(1 ^ 2) → 3
(1 ^ 2)
∴ 3 — Leontiskos
Here is your construal:
[If] 1 and 2 then not 1.
1 and 2.
Therefore not 1. — NotAristotle
Isn't it clear that your construal is mistaken? Try substituting 1, 2, and 3 into each of our construals and see what happens. 1, 2, and 3 are defined in your original argument.
-
Would you agree that your representation of my argument:
...
could also be written as follows...
A. not-3 then not-2. And 2. Then 3.
B. not-3 then not-2. And 2.
C. Therefore 3. — NotAristotle
No, I don't follow this. And you'll need parenthesis and clearer operators if you are trying to transform my propositions. For example, "X then Y" is not a standard usage. You are either omitting 'ifs' or confusing 'then' with the implication sign (→).
So maybe you are right that any argument can be written metalogically as a modus ponens, but I think it cannot be so written without the logical inferences that the argument require, in this case a modus tollens is necessary to the argument and cannot be written off as being a hidden modus ponens. — NotAristotle
But I don't see how your construals are retaining the modus tollens. None of them seem to use modus tollens at all...?
The point about the ubiquity of modus ponens is related to the "therefore" of all arguments. "Therefore" means something like "Hence it follows from the preceding," and that "follows from" move is arguably identical with modus ponens. -
 NotAristotle
587Here is the rewritten formulation of my interpretation of your representation of my argument:
NotAristotle
587Here is the rewritten formulation of my interpretation of your representation of my argument:
A. ((¬3 → ¬2) ^ 2) → 3
B. ((¬3 → ¬2) ^ 2)
C. ∴ 3
Premise B and conclusion C complete the modus tollens. Premise A seems to be something extra. And actually, I think it would make more sense to make premise A a second conclusion as herein:
B. ((¬3 → ¬2) ^ 2)
C. ∴ 3
C2. ((¬3 → ¬2) ^ 2) → 3
It is a second conclusion because it is more of a conclusion derived from premise B, rather than an independent premise that is doing work in the argument.
I do not mind saying my argument metalogically can involve modus ponens, but only incidental to and dependent on it first requiring modus tollens. -
 NotAristotle
587I get what you are saying. However, I maintain that it is strange for me to think of the initial argument of this thread as "valid." In fact, it makes about as much sense to me as
NotAristotle
587I get what you are saying. However, I maintain that it is strange for me to think of the initial argument of this thread as "valid." In fact, it makes about as much sense to me as
A
¬A
therefore,
(B∨¬B)
being "valid." I guess you would say "yeah, but principle of explosion..." but the principle of explosion is also nonsensical to me. -
 Leontiskos
5.6kA. ((¬3 → ¬2) ^ 2) → 3
Leontiskos
5.6kA. ((¬3 → ¬2) ^ 2) → 3
B. ((¬3 → ¬2) ^ 2)
C. ∴ 3
Premise B and conclusion C complete the modus tollens. — NotAristotle
Again, I see no modus tollens there. The inference needed to achieve C is modus ponens, not modus tollens.
Second, let's do the substitutions that I suggested you do. We start with your construal:
A. ((¬3 → ¬2) ^ 2) → 3
B. ((¬3 → ¬2) ^ 2)
C. ∴ 3 — NotAristotle
And we substitute the premises into their places:
A. ((¬[MP is not false] → ¬[RAA is not false]) ^ [RAA is not false]) → [MP is not false]
B. ((¬[MP is not false] → ¬[RAA is not false]) ^ [RAA is not false])
C. ∴ [MP is not false]
That doesn't make any sense to me. It doesn't even include (1) at all, and it doesn't look anything like my own construal:
(1 ^ 2) → 3
(1 ^ 2)
∴ 3 — Leontiskos
...which would be:
([If MP could be false, then RAA could be false] ^ [RAA is not false]) → [MP is not false]
[If MP could be false, then RAA could be false] ^ [RAA is not false]
∴ [MP is not false]
That's valid and intelligible, at least if we don't fret too much about the "could be" modal idea that I have not been fretting about. -
 Michael
16.6kI get what you are saying. However, I maintain that it is strange for me to think of the initial argument of this thread as "valid." — NotAristotle
Michael
16.6kI get what you are saying. However, I maintain that it is strange for me to think of the initial argument of this thread as "valid." — NotAristotle
What do you think "valid" means? It just means that the conclusion can be deduced from the premises using the rules of inference. It doesn't mean that the argument is sound or cogent.
but the principle of explosion is also nonsensical to me. — NotAristotle
1. Either I am a man or pigs can fly
(1) is true if either "I am a man" is true or "pigs can fly" is true. Therefore, we can deduce (1) from the premise "I am a man". This is called disjunction introduction:
P1. I am a man
C1. Therefore, either I am a man or pigs can fly
Separately, we can deduce that if (1) is true and "I am a man" is false then "pigs can fly" is true. This is called disjunctive syllogism:
P1. Either I am a man or pigs can fly
P2. I am not a man
C1. Therefore, pigs can fly
So what happens when we combine the two?
P1. I am man
C1. Therefore, either I am a man or pigs can fly (from P1)
P2. I am not a man
C2. Therefore, pigs can fly (from C1 and P2)
From the contradictory premises "I am a man" and "I am not a man" we have deduced the conclusion "pigs can fly". We can deduce anything from a contradiction. This is part of the reason why we agree that contradictions are impossible. -
 NotAristotle
587I am also not concerned about including any modals in the argument. Let me consider what you stated:
NotAristotle
587I am also not concerned about including any modals in the argument. Let me consider what you stated:
(1 ^ 2) → 3
(1 ^ 2)
∴ 3
— Leontiskos
...which would be:
([If MP could be false, then RAA could be false] ^ [RAA is not false]) → [MP is not false]
[If MP could be false, then RAA could be false] ^ [RAA is not false]
∴ [MP is not false] — Leontiskos
All I am doing is giving more detail to "1."
1 = (¬3 → ¬2)
Given that replacement, premise 2 of the argument as well as the conclusion in line 3 may be written as:
(¬3 → ¬2) ^ 2
∴ 3
My understanding of modus tollens is that it is a logical operation of this form:
(¬A → ¬B)
B
∴ A
But that is the same form as
(¬3 → ¬2) ^ 2
∴ 3
or written otherwise
(¬3 → ¬2)
2
∴ 3
that is why I refer to the second and third lines of the argument as a "modus tollens."
Using the terms you suggested, the modus tollens would be:
(1 ^ 2)
∴ 3
which of course is no modus tollens at all. However that is only because without the detailed replacement for "1" we cannot see that the second and third lines are a veritable modus tollens. -
 NotAristotle
587I agree with the way you defined validity. If I remember correctly, Tones in Deep Freeze defined it formally as an argument whereby there is no interpretation such that all the premises are true and the conclusion is false. I am unclear of what you mean by deduce and deduction. For me, to deduce is to come to a conclusion based on premises where logical principles or inference rules govern the arrival at that conclusion. I see no inference rules being applied in an explosion hypothesis and therefore cannot see it as a deduction at all.
NotAristotle
587I agree with the way you defined validity. If I remember correctly, Tones in Deep Freeze defined it formally as an argument whereby there is no interpretation such that all the premises are true and the conclusion is false. I am unclear of what you mean by deduce and deduction. For me, to deduce is to come to a conclusion based on premises where logical principles or inference rules govern the arrival at that conclusion. I see no inference rules being applied in an explosion hypothesis and therefore cannot see it as a deduction at all. -
 Michael
16.6kI see no inference rules being applied in an explosion hypothesis and therefore cannot see it as a deduction at all. — NotAristotle
Michael
16.6kI see no inference rules being applied in an explosion hypothesis and therefore cannot see it as a deduction at all. — NotAristotle
I explained it above.
P1. I am man
C1. Therefore, either I am a man or pigs can fly (from P1, using disjunction introduction)
P2. I am not a man
C2. Therefore, pigs can fly (from C1 and P2, using disjunctive syllogism) -
 NotAristotle
587I think P2 excludes the possibility of the C1 disjunctive introduction and therefore foils the entire argument.
NotAristotle
587I think P2 excludes the possibility of the C1 disjunctive introduction and therefore foils the entire argument. -
 Michael
16.6kI think P2 excludes the possibility of the C1 disjunctive introduction and therefore foils the entire argument. — NotAristotle
Michael
16.6kI think P2 excludes the possibility of the C1 disjunctive introduction and therefore foils the entire argument. — NotAristotle
If P1 is true then C1 is true. Therefore, the inference is valid.
You seem to be suggesting that if both P1 and P2 are true then it's possible that C1 is false?
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum









