-
 Michael
16.6kWhat's the probability that the two envelopes are filled with {5,10} and the probability that the two envelopes are filled with {10,20}? You know that you're in one of these states given that you just saw 10. — fdrake
Michael
16.6kWhat's the probability that the two envelopes are filled with {5,10} and the probability that the two envelopes are filled with {10,20}? You know that you're in one of these states given that you just saw 10. — fdrake
That depends on how the host selects the values. If he selects a value of X at random from some distribution that includes 5 and 10 then the unconditional probability of {5,10} or {10, 20} being selected is 1/n each (where n is the number of values in the distribution), and so the conditional probability given the £10 in my envelope is 0.5 each.
But if the host selects the value any other way then the objective probabilities will differ. However, assuming the participant doesn't know how the values are selected, he'll just apply the principle of indifference and assume a probability of 0.5 each. -
 JeffJo
175
JeffJo
175
If you did, that statement was completely obfuscated by your sloppy techniques. And it isn't the argument that is flawed, it is the assumption that you know the distribution. As shown by the points you have ignored in my posts.I specifically said that my simulation is not about finding expected results as that entire argument is flawed.
But if that is what you meant, why do you keep pointing out your simulations, which coudl prove something but, as you used them, do not.
The thing to notice here is that you can't use your "X"- the lower value - as a condition unless you see both envelopes, which renders analysis pointless.The thing to notice here is that in all cases the absolute value of the difference between column one and column two is always equal to the lesser of the two (save rounding errors). The lesser of the two is X.
I pointed out a few times that the sample space of event R and the sample space of event S are equal subsets of each other, which means mathematically we can treat them the same.
- A sample space is a set of all possible outcomes. An event is a subset of the sample space. Events don't have sample spaces.
- It not possible for two sets to be unequal subsets of each other.
- We are less concerned with the sample spaces, than with the corresponding probability distributions.
Please, correct me if I am wrong. I have tried to make sense of what you said, but much of it defines all attempts.
This is unintelligble.R and S is the event you have X or 2X when you get A. By definition of A and B, if A=X then B =2X, or if A =2X then B=X. So by definition if A equals X then B cannot also equal X.
Maybe you meant "R and S are events that are conditioned on you having chosen envelope A and it haing the low value or the high value, respectively. If you associate either with a value X from the sample space of possible values, which has nothing to do with R or S, then R means that B must have 2X, and S means that B must have X/2." But you were trying to dissuade Dawnstorm from what appears to have been a valid interpretation of another of your fractured statements; that X was simultaneously possible for both A and B. Even though he realized you could not have meant that, and said as much.
But this still pointless. If you aren't given a value in X, all you need to do is point out that the potential loss is the same as the potential gain. If you are given a value, you do need the distributions. Which you would know, if you read my posts as well I as have (tried to) read yours.
This may be what you were referring to when about "Y." It still refers to ill-defined sets, not distributions.I also pointed out that as soon as you introduce Y they are no longer equal subsets and therefore mathematically cannot be treated the same. -
 fdrake
7.2kBut if the host selects the value any other way then the objective probabilities will differ. However, assuming the participant doesn't know how the values are selected, he'll just apply the principle of indifference and assume a probability of 0.5 each. — Michael
fdrake
7.2kBut if the host selects the value any other way then the objective probabilities will differ. However, assuming the participant doesn't know how the values are selected, he'll just apply the principle of indifference and assume a probability of 0.5 each. — Michael
Right. So there are two cases.
A: One envelope is filled with X and the other 2X.
B: One envelope is filled with X and the other X/2.
Knowing that your envelope has X=10 doesn't let you distinguish between the two cases, right? Same for any value of X.
The values in the envelopes are entirely determined by the case. The cases can't be mixed to obtain a sample space of {X/2,2X} since that's not a possible assignment by the question.
It's also entirely random whether you're observing the thing or its multiple. This means switching has to be averaged within the case (with equal probability assignments for each outcome) and then over the cases (with equal probability assignments for each case). -
 Michael
16.6kRight. So there are two cases.
Michael
16.6kRight. So there are two cases.
A: One envelope is filled with X and the other 2X.
B: One envelope is filled with X and the other X/2.
Knowing that your envelope has X=10 doesn't let you distinguish between the two cases, right? Same for any value of X. — fdrake
Yes, so in case A I gain £10 by switching, in case B I lose £5 by switching, and each case is equally likely. -
 fdrake
7.2k
fdrake
7.2k
If you're in case A, you don't know whether you're in case A. This means you don't know if you gain or lose by switching. Same with case B.
In case A you're assigned either X or 2X.
In case B you're assigned either X or X/2.
I think you're getting hung up on the idea that because you've observed a specific value for X, the other is known. Informally: you have X, yes, but you don't know whether it really is X or 2X. Or in my previous set up. You see U, you don't know whether it is [X or 2X] or [X/2 or X], so you don't know if you gain by switching. -
 Michael
16.6kIn case A you're assigned either X or 2X.
Michael
16.6kIn case A you're assigned either X or 2X.
In case B you're assigned either X or X/2. — fdrake
You're doing it again. It's not possible that we have 2X or X/2 because we've defined X as the value of our envelope. Your cases should be written as:
A: My envelope is X and the other envelope is 2X
B: My envelope is X and the other envelope is X/2
If A is the case then we gain X (10) by switching and if B is the case then we lose X/2 (5) by switching.
Informally: you have X, yes, but you don't know whether it really is X or 2X.
Right, so you're conflating. On the one hand you're defining X as the value of my envelope and on the other hand you're defining X as the value of the smallest envelope. This can be fixed by defining Y as the value of my envelope, and so the value of the other envelope is either 2Y or Y/2.
You see U, you don't know whether it is [X or 2X] or [X/2 or X], so you don't know if you gain by switching.
I know I don't know if I gain by switching. That's not the point. The point is that if I gain then I gain £10, that if I lose then I lose £5, and that each is equally likely. -
 JeffJo
175
JeffJo
175
I hope I'm not talking down, that isn't my point. But probability really needs great care with terminology, and it has been noticeably lacking in this thread. This question is a result of that lack.You're going it again. Is X the value of my envelope or the value of the smallest envelope? You're switching between both and it doesn't make any sense, especially where you say "if you have the lower value envelope X/2".
Let's say that the possible values for envelopes are $5, $10, $20, and $40. This is sometimes called the range of a random variable that I will call V, for the value of your envelope.
A conventional notation for a random variable is that we use the upper case V only to mean the entire set {$5,$10,$20,$40}. If we want to represent just one value, we use the lower case v or an expression like V=$10, or V=v if we want to treat it as unknown.
Each random variable has a probability distribution that goes with it. The problem is, we don't know it for V.
The conditions in the OP mean that there are three possibilities for the pair of envelopes: ($5,$10), ($10,$20), and ($20,$40). Various people have used the random variable X to mean the lower value of the pair; I think you are the only one who has used it to mean what I just called V. So X means the set {$5, $10, $20}. Notice how "$40" is not there - it can't be the low value.
The most obvious random variable is what I have called R (this may be backwards from what I did before). So R=2 means that the other envelope has twice what yours does. Its range is {1/2,2}. It is the most obvious, since the probability for each value is clearly 50%.
From this, we can derive the random variable W, which I use to mean the other envelope. (Others may have confusingly called it Y, or used that for the higher value; they were unclear). Its specific value is w=v*r, so its derived range is {$2.50,$5,$10,$20,$40,$80}. But we know that two of those are impossible. So what we do, is use a probability distribution where Pr(V=$5 & R=1/2)=0, and Pr(V=$20 & R=2)=0. Essentially, we include the impossible values that may come up in calculations in the range, and make them impossible in the probability distribution.
Now, if we don't see a value in an envelope, we know that v-w must be either +x, or -x, with a 50% chance for either. So switching can't help. The point to note is that we don't know what value we might end up with; it could be anything in the full range of V.
Your expectation calculation uses every value of W that is in its range, including the impossible ones. It has to, and that is why they are included in the range. Because of that, you can't use the probabilities for R alone - you need to do something to make $2.50 and $80 impossible.
So you use conditional probabilities for R, not the unconditional ones:
Exp(W|V=v) = (v/2)*Pr(R=1/2|V=v) + (2v)*Pr(R=2|V=v)
= [(v/2)*Pr(R=1/2 & V=v) + (2v)*Pr(R=2 & V=v)] / [Pr(R=1/2 & V=v) + (2v)*Pr(R=2 & V=v)]
We can't separate R and V in those probability expressions, because they are not indepepmndent. But we can if we transform V into X:
= [(v/2)*Pr(R=1/2 & X=v/2) + (2v)*Pr(R=2 & X=v)] / [Pr(R=1/2 & X=v/2) + (2v)*Pr(R=2 & X=v)]
= [(v/2)*Pr(R=1/2)*Pr(X=v/2) + (2v)*Pr(R=2)*(X=v)] / [Pr(R=1/2)*Pr(X=v/2) + (2v)*Pr(R=2)*Pr(X=v)]
And since Pr(R=1/2)=Pr(R=2)=1/2, they divide out:
= [(v/2)*Pr(X=v/2) + (2v)*Pr(X=v)] / [Pr(X=v/2) + (2v)*Pr(X=v)]
Unfortunately, we don't (and can't) know the probabilities that remain. For some values of v, it may be that you gain by switching; but then for some others, you must lose. The average over all possible values of v is no gain or loss.
What you did, was assume Pr(X=v/2) = Pr(X=v) for every value of v. That can never be true. -
 fdrake
7.2k
fdrake
7.2k
As an aside, I think we're saying the same thing from different angles. The fundamental error Michael's making is losing track of what the sample space is and how conditioning works in the problem set up. I've been trying (as have some other people in the thread) to communicate the idea behind:
Now, if we don't see a value in an envelope, we know that v-w must be either +x, or -x, with a 50% chance for either. So switching can't help. The point to note is that we don't know what value we might end up with; it could be anything in the full range of V.
but I'm stumped on how to explain it better. It's pretty clear that Michael thinks conditioning on X makes a difference, which yields an impossible sample space for the problem set up (hence my question on what the raw probability of P(X=the starting value) was, and Michael's answer that it was 'unknown' - which destroys the probability measure he's using). But yeah, don't know how to get it across. -
 Michael
16.6k
Michael
16.6k
I think the disagreement is that you see the situation as this:
Assume there's £10 in one envelope and £20 in the other. If you chose the £10 envelope then switching gains you £10 and if you chose the £20 envelope then switching loses you £10. Each is equally likely and so the average gain from switching over a number of games is £0. Assume there's £10 in one envelope and £5 in the other. If you chose the £10 envelope then switching loses you £5 and if you chose the £5 envelope then switching gains you £5. Each is equally likely and so the average gain from switching over a number of games is £0. This is shown by this simulation.
Whereas I see the situation as this:
Assume there's £10 in my envelope and that one envelope contains twice as much as the other. The other envelope must contain either £5 or £20. Each is equally likely and so the expected value of the other envelope is £12.50. I can then take advantage of this fact by employing this switching strategy to achieve this .25 gain. -
 andrewk
2.1kEven in that more general case, the Bayesian approach can give a switching strategy with a positive expected net gain. Based on our knowledge of the world - eg how much money is likely to be available for putting in envelopes - we adopt Bayesian priors for U and V that are iid. We can use the priors to calculate the expected gain from switching as a function of the observed amount Y. That gain function will be a function that starts at 0, increases, reaches a maximum then decreases, going negative at some critical point and staying negative thereafter. The strategy is to switch if the observed amount Y is less than that critical point.
andrewk
2.1kEven in that more general case, the Bayesian approach can give a switching strategy with a positive expected net gain. Based on our knowledge of the world - eg how much money is likely to be available for putting in envelopes - we adopt Bayesian priors for U and V that are iid. We can use the priors to calculate the expected gain from switching as a function of the observed amount Y. That gain function will be a function that starts at 0, increases, reaches a maximum then decreases, going negative at some critical point and staying negative thereafter. The strategy is to switch if the observed amount Y is less than that critical point.
A simple way to think of this is that it's using the observed value Y to calculate an updated estimate of the Bayesian-updated probability that we have the larger of the two amounts. But because of nonlinearities, the strategy must be based on expected gains rather than just on whether that probability is greater than 0.5.
I like that your post encompasses multiple interpretations. This highlights an important point - that probability is simply a tool, not a fundamental truth about the universe. There is no such thing as 'the absolute probability (or expected value) of Z'. Probabilities are calculated in the context of a probability space, and we are free to set up whatever probability space we like to solve a problem. It is meaningless to say that one probability space is 'correct' and another is 'incorrect'. In finance one uses multiple different probability spaces, with different probabilities assigned to a single event, to analyse risk (eg we often speak of 'risk-neutral' vs 'historical' probabilities). Each probability space serves a different purpose. We can ask whether a probability space appears to help towards achieving its aim, but it makes no sense to ask whether a probability space is correct. -
 fdrake
7.2k
fdrake
7.2k
There's an infinity of well justified approaches if you relax both the equal probability assumptions I used. But yes, probability's just a modelling tool most of the time.
We can ask whether a probability space appears to help towards achieving its aim, but it makes no sense to ask whether a probability space is correct. — andrewk
But so are sample spaces. They're a usually neglected part of model formation since it's usually obvious what all possible values of the measurement are; extreme values of measurements are also pretty easy to eyeball (EG, the probability that an adult human is taller than 3 meters is close to 0) even if more general tail behaviour isn't.
Getting the sample space right in interpretation 2 is an important part of the solution, even when you're using priors to incorporate different information than what's available here from the relationship of the observed value in the envelope to whatever contextual information you deem relevant.
You could also use different loss functions rather than raw expected loss to leverage other contextual information, but I don't see any useful way of doing that here. -
 Michael
16.6kEven in that more general case, the Bayesian approach can give a switching strategy with a positive expected net gain. Based on our knowledge of the world - eg how much money is likely to be available for putting in envelopes - we adopt Bayesian priors for U and V that are iid. We can use the priors to calculate the expected gain from switching as a function of the observed amount Y. That gain function will be a function that starts at 0, increases, reaches a maximum then decreases, going negative at some critical point and staying negative thereafter. The strategy is to switch if the observed amount Y is less than that critical point. — andrewk
Michael
16.6kEven in that more general case, the Bayesian approach can give a switching strategy with a positive expected net gain. Based on our knowledge of the world - eg how much money is likely to be available for putting in envelopes - we adopt Bayesian priors for U and V that are iid. We can use the priors to calculate the expected gain from switching as a function of the observed amount Y. That gain function will be a function that starts at 0, increases, reaches a maximum then decreases, going negative at some critical point and staying negative thereafter. The strategy is to switch if the observed amount Y is less than that critical point. — andrewk
That critical point is going to be the highest that can (will?) be selected by the host, correct? If he selects a value from 1 to 100 for the smaller envelope then you never want to switch if your envelope contains more than 100.
If we do switch only (and always) when our envelope contains £100 or less then we have a gain of 0.25.
I've worked out that the expected gain if we switch only when our envelope is less than or equal to some fixed amount is where is the highest that can (will?) be selected by the host and is our chosen limit for switching. So for , our expected gain for some different values of are:
0 = 0
25 = 0.015625
50 = 0.0625
75 = 0.140625
100 = 0.25
This formula only works if our chosen limit is less than or equal to . I can't figure out the formula for if it's greater. I've only simulated that the rough gains are:
125 = 0.204124
150 = 0.145
175 = 0.080
200+ = 0
Maybe you can work it out? -
 andrewk
2.1k
andrewk
2.1k
Indeed, and that's where utility curves come in. If a parent has a child who will die unless she can get medicine costing M, and the parent can only access amount F, the parent should switch if the observed amount is less than M-F and not switch otherwise.You could also use different loss functions rather than raw expected loss to leverage other contextual information, but I don't see any useful way of doing that here. — fdrake -
 Srap Tasmaner
5.2kIf the game is iterated, so that you can accumulate data about the sample space and its probability distribution, then it's an interesting but completely different problem. We can still talk about strategies in the non-iterative case.
Srap Tasmaner
5.2kIf the game is iterated, so that you can accumulate data about the sample space and its probability distribution, then it's an interesting but completely different problem. We can still talk about strategies in the non-iterative case.
The three choices are:
- Never Switch,
- Always Switch, and
- Sometimes Switch.
There is some evidence that Sometimes Switch increases your expected gain. (I've played around a tiny bit with this, and the results were all over the place but almost always positive. I don't really know how to simulate this.) That's interesting but not quite the "puzzle" here.
If you were trying to find a strategy that is nearly indistinguishable from Never Switch over a large number of trials (not iterated, just repeated), then it would be Always Switch. If, for instance, you fix the value of X, so that there is a single pair of envelopes used over and over again, then we're just talking about coin flips. A Never Switch strategy might result in HTHHTHTT... while Always Switch would be THTTHTHH... and it couldn't be more obvious they'll end up equivalent.
So then the puzzle is what to do about the Always Switch argument, which appears to show that given any value for an envelope you can expect the other envelope to be worth 1/4 more, so over a large number of trials you should realize a gain by always switching. This is patently false, so the puzzle is to figure out what's wrong with the argument.
The closest thing I have to answer is this:
If you define the values of the envelopes as X and 2X for some unknown X, you're fine.
If you want instead to use variables for the value of the envelope you selected, Y, and the value of the one you didn't, U, you can do that. But if you want to eliminate one of them, so you can calculate an expectation only in terms of Y or U, you have to know which one is larger. (Note that there is no ambiguity with X and 2X.) Which one is larger you do not and cannot know.

-
 andrewk
2.1k
andrewk
2.1k
Yes, if we assume a uniform distribution for X on the interval [1,M]. If we assume a more shaped distribution that decays gradually to the right then it will be something different. A gradually changing distribution would be more realistic because it would be strange to say that the probability density of choosing X=x is constant until we reach M and then suddenly plunges to zero. The calculations get messier and hard to discuss without long equations if we use fancy distributions (such as beta distributions or truncated lognormals) rather than a simple uniform distribution. But they can be done.That critical point is going to be the highest XX that can (will?) be selected by the host, correct? — Michael -
 Jeremiah
1.5kEach probability space serves a different purpose. We can ask whether a probability space appears to help towards achieving its aim, but it makes no sense to ask whether a probability space is correct. — andrewk
Jeremiah
1.5kEach probability space serves a different purpose. We can ask whether a probability space appears to help towards achieving its aim, but it makes no sense to ask whether a probability space is correct. — andrewk
It absolutely makes sense to ask if it is correct, and that should be the first question you ask yourself whenever you model something. -
 Pierre-Normand
2.9kIndeed, and that's where utility curves come in. If a parent has a child who will die unless she can get medicine costing M, and the parent can only access amount F, the parent should switch if the observed amount is less than M-F and not switch otherwise. — andrewk
Pierre-Normand
2.9kIndeed, and that's where utility curves come in. If a parent has a child who will die unless she can get medicine costing M, and the parent can only access amount F, the parent should switch if the observed amount is less than M-F and not switch otherwise. — andrewk
Agreed. Alternatively, some player's goal might merely be to maximise the expected value of her monetary reward. In that case, her choice to stick with the initial choice, or to switch, will depend on the updated probabilities of the two possible contents of the second envelope conditional on both the observed content of the first envelope and on some reasonable guess regarding the prior probability distribution of the possible contents of the first envelope (as assessed prior to opening it). My main argument rests on the conjecture (possibly easily proven, if correct) that the only way to characterize the problem such that the (posterior) equiprobability of the two possibilities (e.g. ($10, $20) and ($10, $5)) is guaranteed regardless of the value being observed in the first envelope ($10 only in this case) is to assume something like a (prior) uniform probability distribution for an infinite set of possible envelope contents such as (... , $0.5, $1, $2, ...). -
 Pierre-Normand
2.9kIt absolutely makes sense to ask if it is correct, and that should be the first question you ask yourself whenever you model something. — Jeremiah
Pierre-Normand
2.9kIt absolutely makes sense to ask if it is correct, and that should be the first question you ask yourself whenever you model something. — Jeremiah
You may call one interpretation the correct one in the sense that it provides a rational guide to behavior given a sufficient set of initial assumptions. But it this case, as is the case with most mathematical or logical paradoxes, the initial set of assumptions is incomplete, inconsistent, or some assumptions (and/or goals) are ambiguously stated. -
 Pierre-Normand
2.9kBy this do you just mean that if we know that the value of X is to be chosen from a distribution of 1 - 100 then if we open our envelope to find 150 then we know not to switch? — Michael
Pierre-Normand
2.9kBy this do you just mean that if we know that the value of X is to be chosen from a distribution of 1 - 100 then if we open our envelope to find 150 then we know not to switch? — Michael
That's one particular case of a prior probability distribution (bounded, in this case) such that the posterior probability distribution (after one envelope was opened) doesn't satisfy the (posterior) equiprobability condition on the basis of which you had derived the positive expected value of the switching strategy. But I would conjecture that any non-uniform or bounded (prior) probability distribution whatsoever would likewise yield the violation of this equiprobability condition. -
 Srap Tasmaner
5.2kUnfortunately, we don't (and can't) know the probabilities that remain. For some values of v, it may be that you gain by switching; but then for some others, you must lose. The average over all possible values of v is no gain or loss.
Srap Tasmaner
5.2kUnfortunately, we don't (and can't) know the probabilities that remain. For some values of v, it may be that you gain by switching; but then for some others, you must lose. The average over all possible values of v is no gain or loss.
What you did, was assume Pr(X=v/2) = Pr(X=v) for every value of v. That can never be true. — JeffJo
My first post in this thread three weeks ago:
You're right that seeing $2 tells you the possibilities are {1,2} and {2,4}. But on what basis would you conclude that about half the time a participant sees $2 they are in {1,2}, and half the time they are in {2,4}? That is the step that needs to be justified. — Srap Tasmaner
But I still need help with this.
Yesterday I posted this and then took it down:
Bayes's rule in odds form, which shows that knowing the value of the envelope selected (Y), provides no information at all that could tell you whether you're in a [a/2, a] situation or [a, 2a].
I took it down because the Always Switcher is fine with this, but then proceeds to treat all the possible values as part of one big sample space, and then to apply the principle of indifference. This is the step that you claim is illegitimate, yes? Not the enlarging of the sample space.
Essentially, we include the impossible values that may come up in calculations in the range, and make them impossible in the probability distribution. — JeffJo
Is this the approach that makes it all work?
I kept thinking that Michael's mistake was assuming the sample space includes values it doesn't. (That is, upon seeing Y=a, you know that a or a/2 is in the sample space for X, but you don't know that they both are.) But I could never quite figure out how to justify this -- and that's because it's a mistaken approach?
Unfortunately, we don't (and can't) know the probabilities that remain. For some values of v, it may be that you gain by switching; but then for some others, you must lose. The average over all possible values of v is no gain or loss. — JeffJo
Right and that's what I saw above -- the odds X=a:X=a/2 are still whatever they are, and still unknown.
Your last step, averaging across all values of V, I'm just trusting you on. Stuff I don't know yet. Can you sketch in how you handle the probability distribution for V? -
 Michael
16.6kSo then the puzzle is what to do about the Always Switch argument, which appears to show that given any value for an envelope you can expect the other envelope to be worth 1/4 more, so over a large number of trials you should realize a gain by always switching. This is patently false, so the puzzle is to figure out what's wrong with the argument. — Srap Tasmaner
Michael
16.6kSo then the puzzle is what to do about the Always Switch argument, which appears to show that given any value for an envelope you can expect the other envelope to be worth 1/4 more, so over a large number of trials you should realize a gain by always switching. This is patently false, so the puzzle is to figure out what's wrong with the argument. — Srap Tasmaner
In half the games where you have £10 you switch to the envelope with an expected value of £12.50 and walk away with £20. In half the games where you have £20 you switch to the envelope with an expected value of £25 and walk away with £10. The gain from the first game is lost in the second game.
It's because of this that you don't gain in the long run (given that some X is the highest X and every game where you have more than this is a guaranteed loss), and it's with this in mind that I formulated my strategy of only switching if the amount in my envelope is less than or equal to half the maximum amount seen, which I've shown does provide the expected .25 gain (which is no coincidence; the math I've been using shows why the gain is .25). And if we're not allowed to remember previous games then the formula here shows the expected gain from some arbitrarily chosen limit on when to switch, peaking at .25.
So as a simple example, you switch when it's £10 into an envelope with an expected value of £12.50 and walk away with £20 and stick when it's £20 because you don't want to risk losing your winnings from the first game. In total you have £40. The person who sticks both times has £30. You have .25 more than him.
Also, that article you provided refers to this paper which shows with some simulations that the expected gain from following their second switching strategy averages at .25 (thick black lines at top):
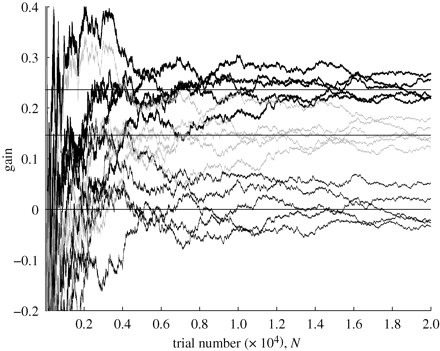
-
 Jeremiah
1.5kNo amount of "math" will ever change the actual contents of the envelopes. Some of you are just pushing numbers around on the page, but math is not magic, it can't change the actual dollar values.
Jeremiah
1.5kNo amount of "math" will ever change the actual contents of the envelopes. Some of you are just pushing numbers around on the page, but math is not magic, it can't change the actual dollar values.
And I know I am just speaking in the wind at this point, but we could physically set this game up, using various dollar amounts and you'd never get the expected gain some here are predicting. You can't just think about the numbers, you have to think about the actual outcome. -
 Michael
16.6kAnd I know I am just speaking in the wind at this point — Jeremiah
Michael
16.6kAnd I know I am just speaking in the wind at this point — Jeremiah
Well, you did say here that "[you are] already convinced [your] approach is correct... [you] have no doubt about it, and [you] no longer care about arguing or proving that point".
So I don't know why you keep posting or why you'd expect anyone to address you further.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum







