-
 Zuhair
132I'll use here some personal terminologies, I hope it won't be disturbing.
Zuhair
132I'll use here some personal terminologies, I hope it won't be disturbing.
We may divide truths into two kinds: receptive and consequential.
With the first kind I mean truths that are external to our makings and procedures, that
impose itself on us, that our main stance from it is that of "receiving it", like for example that the earth orbits the sun, that the sun is bigger than earth, like water is composed of hydrogen and oxygen, etc.. those are truths that impinge itself on us and we have no choice but to accept them as such, and to discover them we need to use apparatus related to detecting them, primarily being our five senses, devices, etc..We can call such truths as reality kind of truths.
The other kind of truth is what I label as "consequential", here this kind of truth has a human role
in delivering it, for example we begin with an arbitrary set of rules, and see were those rules lead us to. A simple example is to have a rule that: R is transitive (if x R y R z then x R z), and another rule stating that there are objects x,y,z,u such that x R y R z R u R x, then from these two rules we'll have the following 12 consequences:
x R z, x R u, x R x, y R u , y R x, y R y, z R x, z R y, z R z, u R y, u R z, u R u.
The fellowship of those consequences from the two input rules is a kind of TRUTH. This is a consequential fact. In the sense that we are obligated to hold that those outcomes are the results of applications of the input rules. The main difference between the consequential and the receptive kind, is that with the consequential kind we have control over the conditions from which we harvested that truth, while with the receptive kind we don't control the medium from which that truth sprang. Now consequential truth might lead to outcomes that might oppose receptive truths (reality truths), for example: if we input the rule that all Males have XX chromosomes, the rule that Napoleon is a male, then the outcome is Napoleon has XX chromosomes. Here this outcome is against reality, but as a consequence of the aforementioned rules, the consequence itself is TRUE, i.e. it is TRUE that if we hold the first inputs to be true then it follows that the outcome is true.
Emmanuel Kant once spoke about what he termed as ANALYTIC truths, like in the sentence "All bald men are bald". which is a kind of affirmation consequential rule. Here the consequential rule is about "are", it affirms the acquisition of a predicate before it, so the general rule is ALL objects that possess predicate phi ARE in possession of predicate phi. Another way is to break it downs to rules related to conjunction and implication: that is [A & B -> A] , [ A & B -> B]. This is just a rule following scenario, so what he called as "analytic" fact, is actually nothing but a kind of consequential truth.
Once Hume had said that mathematics is absolute because it deals with those kinds of analytic truths, so 2+2=4, comes from the roles assigned to the symbols 2, +, =. The complete story is if we hold the rules of the game of arithmetic, then we'll have 2+2=4 being an outcome (a consequence) of this game. This is absolute, because the rules are put in absolute manner. And it is a kind of TRUTH.
Here I'm stating a similar stance that is: Mathematics is the study of consequential truth.
So mathematics is about studying rule following games. I call them games because the choice of the primary rules is IMMATERIAL, we can even call them ARBITRARY, the most important is to harvest consequential truths in those games. The reality of the games, i.e. the stance of its primary rules and consequential outcomes from reality, is not relevant to mathematics itself, it is however relevant to its application, but not to mathematics per se.
As such mathematics need not essentially have an application. However, that doesn't meant that it ought not to. On the contrary SOME parts of mathematics do have many applications, and those parts have their primary rules related in some sense to reality, that's why it had applications, and thus were significant in increasing our knowledge about reality, some parts of reality are rule driven, so examining rule driven scenarios can be related to reality. Applied mathematics is the part of mathematics whose primary rules can be said to have some connection to reality and so can be labeled as quasi-empirical or the alike.
Of course it would be understandable that only beneficial rule following games would survive, and be studied more. However, that is not truly the primary job of the mathematician, the mathematician is concerned with consequential truths in rule following games, she\he has nothing to do with justification of the primary rules of those games from the perspective of match-ability with reality.
So what I'm advocating here is a line in philosophy of mathematics that can be termed as: consequential-ism. So mathematicians negotiate themselves with scenarios fruitful in consequential thought and study the consequential outcomes of those scenarios.
So mathematics per se is not necessarily empirical or quasi-empirical, although some parts of mathematics can be so.
There is the point of view that even if mathematics is not about reality-matching rule following games, yet it is about some kind of platonic realm matching. In other words mathematicians are somehow perceiving a kind of reality that is not the concrete physical reality, and that mathematical truths can be seen as a kind of receptive truth about that realm. This is what is generally labeled as mathematical Platonism.
The main problem with this viewpoint is that it is to strong, for although a working mathematician when he brings about some new mathematical rules or define new objects, he's indeed working within such context, that it appears as if they he is "discovering" those, but at the and of the day, no such a claim would be granted or even posed. What is granted is the consequential facts of his work, and it is that what counts. While its stance from such realm or even from reality is not even posed.
This philosophical line doesn't assert any of the known prior logical schools in philosophy of mathematics, so it is not to be confused with logicism, nor with formalism (which is the nearest to it), nor with nominalism, or structuralism, nor with fictionalism.
Here I'm not asserting that the rule following games must be purely logical (has no extra-logical primitive concepts), or that mathematics is nothing but a string manipulation rules of meaningless (empty) symbols. I'm simply saying that the rule following game can be of ANY motivation even empirically motivated, but if the sole study of it was as a rule following device, and the study was just for the consequential load of it, then it is a mathematical study. It can be a meaningful game, where meaning itself is stipulated through rules, so it would be a meaning rule manipulating system, it can also be an empty string of symbols rule manipulating system. It doesn't matter how much meaning are there and their stance from reality or even from a platonic realm, or from apriori concepts, what counts is the consequential bearings of those games.
So mathematics is the study of consequential truths in rule following games.
Of course this study does include heuristics involved in bringing about such games, and bringing about useful definitions and proofs in those games, for although those heuristics themselves are not decided by the primary rules themselves, yet they are finally about consequential bearing within those scenarios. Those heuristics can virtually have imports from any realm of thought actually, logical, apriori, structural, platonic, pragmatic, empirical, formal, etc.. so there is no limit to it, and it constitutes the mathematical ingenuity no doubt. But mathematics cannot be defined after those heuristics, since such a thing is clearly un-definable. That ingenuity can be understood as the tool that leads us to bring about mathematical systems, rather than it itself being identified with mathematics. Mathematics is the consequential bearings that this ingenuity finds in what it creates of rule following games. So philosophy of mathematical practice is not identical with that of mathematics.
What are the drawbacks of that personal line of thought of mine about philosophy of mathematics. -
 alcontali
1.3kWe may divide truths into two kinds: receptive and consequential. — Zuhair
alcontali
1.3kWe may divide truths into two kinds: receptive and consequential. — Zuhair
I do not particularly appreciate the use of the term "truth" in the context of mathematics. The quite dominant Correspondence theory of truth defines "truth" as:
In epistemology, the correspondence theory of truth states that the truth or falsity of a statement is determined only by how it relates to the world and whether it accurately describes (i.e., corresponds with) that world. Correspondence theories claim that true beliefs and true statements correspond to the actual state of affairs. This type of theory attempts to posit a relationship between thoughts or statements on one hand, and things or facts on the other.
Mathematics never talks about the real, physical world, because claiming such a thing, is simply a constructivist heresy.
Mathematics is exclusively and only about theorems that are provable from the construction logic of the abstract, Platonic world, i.e. the theory, generated by a particular arbitrary set of axioms.
Since we do not have access to the axiomatic construction logic of the real, physical world, i.e. the theory of everything (ToE), mathematics cannot possibly ever be about the real, physical world. Ever.
Therefore, the use of the term "truth" in mathematics, is always heretical, and I do not wish to participate in the propagation of that kind of horrible heresies.
The fellowship of those consequences from the two input rules is a kind of TRUTH. This is a consequential fact. — Zuhair
These consequences are merely provable from these rules. They are not "true" in any possible fashion. Provability (PR) and correspondence-theory truth (CT) have absolutely nothing to do with each other.
CT truth and logical truth (LT) have also nothing to do with each other. For example, in "var b = true" the variable b does not correspond to anything in the real, physical world, but we cannot deny that it is logically true, if only, because we defined it to be.
Provability (PR) and logical truth (LT) have also nothing to do with each other. For example, in first his incompleteness theorem, Gödel encodes a statement that is logically true but not provable.
A lot of wrong views and other errors are the result of confusing CT, LT, and PR.
Here I'm stating a similar stance that is: Mathematics is the study of consequential truth. — Zuhair
Mathematics is fundamentally reductionist.
In mathematics, reductionism can be interpreted as the philosophy that all mathematics can (or ought to) be based on a common foundation, which for modern mathematics is usually axiomatic set theory.
Of course, I totally disagree with the idea that any choice of axioms would be better than any other choice. Therefore, I utterly reject the idea that set theory would be a better foundation than any other Turing-complete axiomatization. So, I must protest against this particular detail with the following formalist objection:
Formalism holds that mathematical statements may be thought of as statements about the consequences of certain string manipulation rules. According to formalism, mathematical truths are not about numbers and sets and triangles and the like—in fact, they are not "about" anything at all. Formalism is thus silent on the question of which axiom systems ought to be studied, as none is more meaningful than another from a formalistic point of view.
(Note: I also protest against the use of the term "mathematical truths" in the fragment above.) -
 fdrake
7.2k
fdrake
7.2k
How do you both deal with that people wrestle with axioms as much as theorems? The Hilbert program's legacy (and logicism) is on the one hand to find a unifying logical system for all mathematics (which failed, strictly speaking), but the more pernicious legacy is thinking of mathematical theories as given by their axioms. Which is true in a logical/model theoretic sense, but what's really interesting about axiomatisations is how they allow mathematical structures to flower from them.
For a mathematical analogy; imagine that you have an idea of a structure you want to capture the behaviour of, and you have the behaviour, taking a 'pre-image' of that behaviour (through provability) to the axioms which engender it is just as vital a part of mathematics. If ever you've tried to axiomatise a structure you'd see that there's a reciprocality between the structure's concept and its mathematical definition. -
 alcontali
1.3kimagine that you have an idea of a structure you want to capture the behaviour of, and you have the behaviour — fdrake
alcontali
1.3kimagine that you have an idea of a structure you want to capture the behaviour of, and you have the behaviour — fdrake
A weird aspect of math is that "behaviour" means, "respectful of particular invariants", such as e.g. :
a ⊕ b = b ⊕ a
commutativity or so. In (software) programming, it means being able to execute a particular function, e.g.
a->f(b)
where "a" is capable of looking up a function "f" and apply it to a given argument. I personally find programming with invariants to be much harder than with functions ... but ultimately probably also more powerful.
If ever you've tried to axiomatise a structure you'd see that there's a reciprocality between the structure's concept and its mathematical definition. — fdrake
With the term "structure", do you mean structure as in "algebraic structure", i.e. a set with a collection of operations? Such as a group (K,+) of set K and the addition operation?
Saying that it is a "group" automatically attaches a set of invariants. If you add enough invariants to the structure, i.e. you may use up all your degrees of freedom, then indeed, at some point there will only be one candidate definition that fits the bill. It could, for example, leave only one K possible. You could obviously also over-specify and propose the structure of something that cannot possibly exist.
I think that you can treat K as an unknown, or even one of the operations (why not?), but that will probably lead to specifying a non-trivial higher-order logic problem.
Are you trying to program a structure by attaching invariants? -
 alcontali
1.3kAny form of reflection on the "world" or "states of affairs" concerns facts, and facts are always historical. Are you prepared to assert that all facts are true - without some weird question-begging qualification? — tim wood
alcontali
1.3kAny form of reflection on the "world" or "states of affairs" concerns facts, and facts are always historical. Are you prepared to assert that all facts are true - without some weird question-begging qualification? — tim wood
Yes, but subject to the scrutiny of the historical method.
My own definition of truth, fwiw, is that "truth" is an abstract term that simply means that the proposition in question complies with an appropriate standard in being true, while being entirely agnostic as to what that standard is. — tim wood
Well, polymorphism is obviously permissible as long as it does not lead to fundamentally ambiguous situations ... -
 alcontali
1.3kIf by polymorphism you mean that truth can take different forms, I disagree, because on my definition, "truth" is defined to accommodate all forms, as qualified, because that is the best it can do. — tim wood
alcontali
1.3kIf by polymorphism you mean that truth can take different forms, I disagree, because on my definition, "truth" is defined to accommodate all forms, as qualified, because that is the best it can do. — tim wood
Polymorphism is first and foremost a language thing. I am not sure if it exists in the real, physical world. Maybe it does somewhere that I am not aware of. Polymorphism is obviously all over the place in software, like for example in duck typing:
Duck typing in computer programming is an application of the duck test—"If it walks like a duck and it quacks like a duck, then it must be a duck"—to determine if an object can be used for a particular purpose. With normal typing, suitability is determined by an object's type. In duck typing, an object's suitability is determined by the presence of certain methods and properties, rather than the type of the object itself.
So, yes, the practice is allowed, also in language in general (such as natural language), but the ever-present danger is: ambiguity.
And I cannot think of a fundamentally ambiguous situation. — tim wood
It is not necessarily the real world, or its situations, that are ambiguous. However, language definitely is: Every bug is an ambiguity and every ambiguity will sooner or later lead to a bug. The losing war against bugs is in reality one against ambiguity. -
 Zuhair
132Thank you for your opinion about terminology about truth. But the essence of the matter of difference between us here (as it appears to me ) is just a matter of terming things. What you call TRUTH which is "correspondence with reality" according to the epistemology theory you've cited, I call as "receptive truth" or even it might be better called as "reality correspondence truth", I'm explicitly stating in my message that mathematics is not about that concept. I in opposition to your terminology prefer to use the term truth to denote another context which is quite different from the "correspondence with reality" context, and that context is what I've labeled as "consequential truth", you are free not to call it truth, you may term it as "consequentiality", or "consequential processing" which are fair enough. I explicitly gave an example where those two concepts collide. But to me I prefer to call it consequential truth, which is of course something that is quite different from correspondence truth. what I'm saying is that mathematics is about consequentiality. The mathematical systems are just mediums in which consequential processing is carried in. Also I traced back Analytic truths of I. Kant into consequential rule following processes. And I think mathematics is nothing but about such consequential machinery.
Zuhair
132Thank you for your opinion about terminology about truth. But the essence of the matter of difference between us here (as it appears to me ) is just a matter of terming things. What you call TRUTH which is "correspondence with reality" according to the epistemology theory you've cited, I call as "receptive truth" or even it might be better called as "reality correspondence truth", I'm explicitly stating in my message that mathematics is not about that concept. I in opposition to your terminology prefer to use the term truth to denote another context which is quite different from the "correspondence with reality" context, and that context is what I've labeled as "consequential truth", you are free not to call it truth, you may term it as "consequentiality", or "consequential processing" which are fair enough. I explicitly gave an example where those two concepts collide. But to me I prefer to call it consequential truth, which is of course something that is quite different from correspondence truth. what I'm saying is that mathematics is about consequentiality. The mathematical systems are just mediums in which consequential processing is carried in. Also I traced back Analytic truths of I. Kant into consequential rule following processes. And I think mathematics is nothing but about such consequential machinery.
Although terminology is of course important for understanding, but I think one better try negotiate the essence of what's presented. -
 alcontali
1.3kI in opposition to your terminology prefer to use the term truth to denote another context which is quite different from the "correspondence with reality" context, and that context is what I've labeled as "consequential truth", you are free not to call it truth, you may term it as "consequentiality", or "consequential processing" which are fair enough. — Zuhair
alcontali
1.3kI in opposition to your terminology prefer to use the term truth to denote another context which is quite different from the "correspondence with reality" context, and that context is what I've labeled as "consequential truth", you are free not to call it truth, you may term it as "consequentiality", or "consequential processing" which are fair enough. — Zuhair
"Consequential truth" sounds very much like Coherence theory of truth.
In epistemology, the coherence theory of truth regards truth as coherence within some specified set of sentences, propositions or beliefs. The model is contrasted with the correspondence theory of truth. A positive tenet is the idea that truth is a property of whole systems of propositions and can be ascribed to individual propositions only derivatively according to their coherence with the whole.
"Coherence" in mathematics is obviously axiomatic (=reductionist). Fundamentally, I object to this view because it turns "truth" into some kind of calculation. Any such calculation can be not just arbitrarily faulty, but also fundamentally misguided.
Perhaps the best-known objection to a coherence theory of truth is Bertrand Russell's. He maintained that since both a belief and its negation will, individually, cohere with at least one set of beliefs, this means that contradictory beliefs can be shown to be true according to coherence theory, and therefore that the theory cannot work.
As Bertrand Russell argued, naive approach to coherence would clearly lead to contradictions.
However, what most coherence theorists are concerned with is not all possible beliefs, but the set of beliefs that people actually hold. The main problem for a coherence theory of truth, then, is how to specify just this particular set, given that the truth of which beliefs are actually held can only be determined by means of coherence.
At the same time, a selective approach is not really possible, because it is automatically circular.
I think that the better term for "consequential truth" in mathematics is "provability". It captures much better the status of mathematical theorems. If a theorem necessarily follows from a set of rules, then the theorem is "provable from" these rules. Why use the controversial term "truth" instead of "provability"? Especially given the fact that the rules from which a theorem is proven, do not need to be "true" in any sense ... -
 fdrake
7.2kAre you trying to program a structure by attaching invariants? — alcontali
fdrake
7.2kAre you trying to program a structure by attaching invariants? — alcontali
Eh. Structure's a placeholder there. Generally they'll be algebraic flavour, a collection of objects and operations or relators between them.
Saying that it is a "group" automatically attaches a set of invariants. If you add enough invariants to the structure, i.e. you may use up all your degrees of freedom, then indeed, at some point there will only be one candidate definition that fits the bill. It could, for example, leave only one K possible. You could obviously also over-specify and propose the structure of something that cannot possibly exist. — alcontali
I mean something like the following construction. Let's say we've fixed a vocabulary of symbols and interpretations for all the things we're considering. Say you've got sets of axioms and sets of inference rules that allow you to derive consequences from the axiomatic systems. Let's imagine that we have a bunch of consequences we know we need to reproduced; like 1+1=2 or 'avoid Russell's paradox", or "greater temperature contrasts between medium and immersed object yield more rapid temperature exchange" or something like that.
They're not really all the same thing, 1+1=2 is a specified theorem and a relation of formal objects, 'avoid Russel's paradox' is place a limitation on the space of theorems to avoid a nasty one, and 'greater temperature contrasts...' isn't even directed toward a mathematical object, it's trying to fit a bunch of mathematical objects to the world to describe a part of it.
Regardless, let's say that our end result is the grand 'ole , the thing we wanna do implemented in a mathematical system. Let's just gloss over that the objects in need not be mathematical in nature; nature can shout NO to any model of it and formalisms can be wrongheaded or irrelevant. This is mostly setting up a flowchart rather than a mathematical argument. Anyway
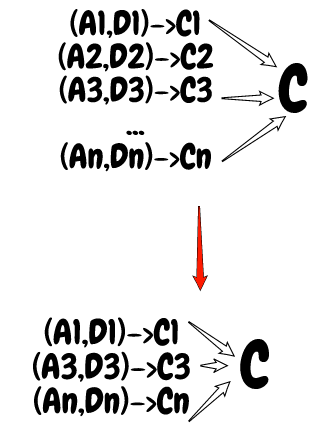
We find out what axiomatic systems give what conclusions, but notice that the conclusions that we desire are the motivating feature in this diagram. Allow after the red arrow to be interacted with other objects and goals, and you have a picture of mathematical progress.
Pure formalism just gives you the black arrows, it does not give the sense of mathematical progress through the articulation and codification of ideas, just the dynamics of symbols, as if the ideas motivating them were completely irrelevant. Another way of putting it: formalism is just what we invent to get to where we need to go. -
 alcontali
1.3kWe find out what axiomatic systems give what conclusions, but notice that the conclusions that we desire are the motivating feature in this diagram. — fdrake
alcontali
1.3kWe find out what axiomatic systems give what conclusions, but notice that the conclusions that we desire are the motivating feature in this diagram. — fdrake
There seems to be an entire area of research on axiomatic subsystems of second-order arithmetic (Z2). It is apparently about crippling Peano arithmetic and check what's left over. Presburger and Robinson are examples of this, but there are also other variations.
Pure formalism just gives you the black arrows, it does not give the sense of mathematical progress through the articulation and codification of ideas, just the dynamics of symbols, as if the ideas motivating them were completely irrelevant. Another way of putting it: formalism is just what we invent to get to where we need to go. — fdrake
I think that they do not care, for example, in Z2 research. They're just interested in what the effect is of the crippling on the resulting arithmetic. For example:
Skolem arithmetic is the first-order theory of the natural numbers with multiplication, named in honor of Thoralf Skolem. The signature of Skolem arithmetic contains only the multiplication operation and equality, omitting the addition operation entirely.
It is actually interesting stuff. I am surprised that this botched version of arithmetic still seems to work. -
 Zuhair
132I'll make a more elaborate response to this nice posting later. But for now I just want to resolve any misunderstanding that my prior response might have caused. What I'm really saying is that we can have many kinds of truths, there is a receptive kind of truth which is was you've mentioned by the correspondence theory, you can call it correspondence truth if you like, and there is another kind of truth which is what I call as consequential truth, you may consider it as a kind of coherence truth (or possibly the converse is true?! i.e. coherence truth is a kind of consequential truth, since formalism might have zero meaning but it does involve consequence, it's nice to explore that issue). The first kind is involved in empirical sciences, the second kind is involved in mathematics and logic (although I generally consider logic to be part of mathematics). The first answers to what the real world is? the second answers to what outcomes results from pre-specified rules. They are different concepts! I like the term "consequential truth" because I see it directly engaging the concept it negotiates. The term "provability" is more complex, it can even be said to be more or less a mathematical term, so I cannot define mathematics after it, since this would be a kind of a circular definition, but if we can manage cut from it the mathematical detail, then it might serve the same purpose of consequential truth. I also oppose to the idea of reductionism in mathematics, since this already proved to be false anyway. It is nice to reduce of course mathematical theories to simpler ones, but in my stance here all theories are equal, since all of them are just games, what's really important is the consequential truths in them. In nutshell you can say that:
Zuhair
132I'll make a more elaborate response to this nice posting later. But for now I just want to resolve any misunderstanding that my prior response might have caused. What I'm really saying is that we can have many kinds of truths, there is a receptive kind of truth which is was you've mentioned by the correspondence theory, you can call it correspondence truth if you like, and there is another kind of truth which is what I call as consequential truth, you may consider it as a kind of coherence truth (or possibly the converse is true?! i.e. coherence truth is a kind of consequential truth, since formalism might have zero meaning but it does involve consequence, it's nice to explore that issue). The first kind is involved in empirical sciences, the second kind is involved in mathematics and logic (although I generally consider logic to be part of mathematics). The first answers to what the real world is? the second answers to what outcomes results from pre-specified rules. They are different concepts! I like the term "consequential truth" because I see it directly engaging the concept it negotiates. The term "provability" is more complex, it can even be said to be more or less a mathematical term, so I cannot define mathematics after it, since this would be a kind of a circular definition, but if we can manage cut from it the mathematical detail, then it might serve the same purpose of consequential truth. I also oppose to the idea of reductionism in mathematics, since this already proved to be false anyway. It is nice to reduce of course mathematical theories to simpler ones, but in my stance here all theories are equal, since all of them are just games, what's really important is the consequential truths in them. In nutshell you can say that:
Empiricism is about correspondence and Mathematics is about consequence. -
 Wittgenstein
442
Wittgenstein
442
Can you list your complete set of axioms for arithmetic in a system where godels theorem doesn't apply. ( it cannot be recursively innumerable )
CT truth and logical truth (LT) have also nothing to do with each other. For example, in "var b = true" the variable b does not correspond to anything in the real, physical world, but we cannot deny that it is logically true, if only, because we defined it to be.
Provability (PR) and logical truth (LT) have also nothing to do with each other. For example, in first his incompleteness theorem, Gödel encodes a statement that is logically true but not provable
I would say that tautology and contradiction have nothing to do with CT truth but the truth value of the rest of propositions are linked with CT truth. Second of all, we can define probability of a proposition to mean assigning truth value ( T or F) . In that case, l dont think godels theorem would work. It will be great if we can create a discussion to understand the incompleteness theorem. -
 Wittgenstein
442
Wittgenstein
442
So mathematics is about studying rule following games. I call them games because the choice of the primary rules is IMMATERIAL, we can even call them ARBITRARY, the most important is to harvest consequential truths in those games. The reality of the games, i.e. the stance of its primary rules and consequential outcomes from reality, is not relevant to mathematics itself, it is however relevant to its application, but not to mathematics per se.
If rules are arbitrary, would you allow contradictions in it.
Will a system have logically interlinked rules such that they have to be consistent and if so, they won't be arbitrary strictly speaking. Will a different system be created by only removing certain rules or creating new ones. How would you create new rules ? -
 SophistiCat
2.4kThat's a lot of words, but I am kind of struggling to understand what it is that you think is the original thought here. How is your receptive/consequential distinction different from synthetic/analytic, etc. - what has become known as "Hume's fork" (and has since been deconstructed and criticized by Quine, etc.)?
SophistiCat
2.4kThat's a lot of words, but I am kind of struggling to understand what it is that you think is the original thought here. How is your receptive/consequential distinction different from synthetic/analytic, etc. - what has become known as "Hume's fork" (and has since been deconstructed and criticized by Quine, etc.)? -
 Zuhair
132it depends on what kind of arithmetic you have in mind. Anyhow you can of course list a complete set of axioms for arithmetic that is not recursively enumerable, this is easy take for example PA+omega rule.
Zuhair
132it depends on what kind of arithmetic you have in mind. Anyhow you can of course list a complete set of axioms for arithmetic that is not recursively enumerable, this is easy take for example PA+omega rule.
As regards provability and logical truth, one needs to be careful, what Godel has proved is that some theories cannot prove all statements made in their language, so there would be statements that the theory neither denies nor proves. That's all, this is about completeness of theories. From the perspective of this account this would be phrased as: some rule following games can have statements written in their language that has no consequential truth from the rules of those games nor do their negation has, because they are neither consequences of those rules nor is their negations. Godel demonstrated that for some theory T there can be a sentence S written in the language of T such that S is equivalent to statement "S is not provable in T", so obviously if T is consistent, then T cannot prove S. Be aware that this doesn't entail that S is a consequential truth of T, no! For S can be false and T be inconsistent! When we say that S is a logical truth, this is actually mean that S is a consequential truth of the theory T + Con(T), where "Con(T)" is the statement "T is consistent". In other words S is provable in T+Con(N), that's why its said to be a logical truth, in reality it means that it is a consequential truth from the rule following game T+Con(N), notice that it is not a consequential truth of T itself. "Logical truth" is provability in some system. So it is a relative concept. In other words S is not a logical truth of T, the logical truths of T are the theorems of T only.
I don't know what you mean that all propositions other than tautologies and contradictions has Correspondence truth. Correspondence with what? with Reality? what's Reality? I think this is mistaken, those propositions has no innate truths in them, rather truth is assigned to them by the system by dictation (if they are axioms) or by being consequential truths following from the rules of the game.
As regards your second reply, my answer is YES, inconsistent rule following games are definitely mathematical as far as our study of them is about the consequential truth of them.
I didn't get your question about how to create new rules, you simply stipulate them or they are consequences of newly stipulated rules? what's the problem? -
 Zuhair
132analytic truth truth by virtue of the meaning of the words of a statement, synthetic needs meaning and correspondence with reality as well. Here with this terminology I'm speaking about rule following which can even be of strings of empty symbols, so meaning is not involved here, however synthetic seems to be overlapping with receptive truths. I think that analytic is "meaningful consequential truths", so I think the term "consequential truth" is weaker than analytic truth, although of course you can object to this by holding that consequential truth is a kind of non-meaningful analytic truth or by saying that rule fellowship is a kind of meaning, you can call it meaning by having a role in following a rule, if so then we can subsume consequential into analytic. The new things is that KANT was saying that mathematics is apriori synthetic. Which this philosophy doesn't agree with. I more agree with Hume that mathematics is purely analytic nothing else. Regarding Quine's criticism he never criticized the substitutional form of analytic truths, on the contrary he considered it non problematic at all, he only criticized the meaningful kind of analytic truth. Here in this account the "consequential" part is more akin to the substitutional form of analytic truth although not necessarily limited to symbols, it can incorporate meaning but only if strictly manipulated by rule following games, which of course works by combinative-substitutional machinery. So there is some difference, as minor as it may be, but there is.
Zuhair
132analytic truth truth by virtue of the meaning of the words of a statement, synthetic needs meaning and correspondence with reality as well. Here with this terminology I'm speaking about rule following which can even be of strings of empty symbols, so meaning is not involved here, however synthetic seems to be overlapping with receptive truths. I think that analytic is "meaningful consequential truths", so I think the term "consequential truth" is weaker than analytic truth, although of course you can object to this by holding that consequential truth is a kind of non-meaningful analytic truth or by saying that rule fellowship is a kind of meaning, you can call it meaning by having a role in following a rule, if so then we can subsume consequential into analytic. The new things is that KANT was saying that mathematics is apriori synthetic. Which this philosophy doesn't agree with. I more agree with Hume that mathematics is purely analytic nothing else. Regarding Quine's criticism he never criticized the substitutional form of analytic truths, on the contrary he considered it non problematic at all, he only criticized the meaningful kind of analytic truth. Here in this account the "consequential" part is more akin to the substitutional form of analytic truth although not necessarily limited to symbols, it can incorporate meaning but only if strictly manipulated by rule following games, which of course works by combinative-substitutional machinery. So there is some difference, as minor as it may be, but there is. -
 SophistiCat
2.4kanalytic truth truth by virtue of the meaning of the words of a statement, synthetic needs meaning and correspondence with reality as well. Here with this terminology I'm speaking about rule following which can even be of strings of empty symbols, so meaning is not involved here, however synthetic seems to be overlapping with receptive truths. I think that analytic is "meaningful consequential truths", so I think the term "consequential truth" is weaker than analytic truth, although of course you can object to this by holding that consequential truth is a kind of non-meaningful analytic truth or by saying that rule fellowship is a kind of meaning, you can call it meaning by having a role in following a rule, if so then we can subsume consequential into analytic. The new things is that KANT was saying that mathematics is apriori synthetic. Which this philosophy doesn't agree with. I more agree with Hume that mathematics is purely analytic nothing else. — Zuhair
SophistiCat
2.4kanalytic truth truth by virtue of the meaning of the words of a statement, synthetic needs meaning and correspondence with reality as well. Here with this terminology I'm speaking about rule following which can even be of strings of empty symbols, so meaning is not involved here, however synthetic seems to be overlapping with receptive truths. I think that analytic is "meaningful consequential truths", so I think the term "consequential truth" is weaker than analytic truth, although of course you can object to this by holding that consequential truth is a kind of non-meaningful analytic truth or by saying that rule fellowship is a kind of meaning, you can call it meaning by having a role in following a rule, if so then we can subsume consequential into analytic. The new things is that KANT was saying that mathematics is apriori synthetic. Which this philosophy doesn't agree with. I more agree with Hume that mathematics is purely analytic nothing else. — Zuhair
Right, so your receptive/consequential distinction falls approximately along the same line as Hume's matters of fact vs. relations of ideas, which is now often aliased as synthetic/analytic, although one can certainly split semantic hairs and introduce further distinctions, like Kant's a priori/a posteriori. (For that matter, Hume's own treatment of relations of ideas amounted to more than just rule-following.) In any event, this is a well-trodden path - I was just wondering whether you thought you were bringing some fresh perspective and not just your personal terminology.
The idea that all there is to mathematics is manipulation of symbols according to fixed rules is true only within a comparatively limited, 18th century conception of mathematics, when mathematics was the mathematics, and it sprang from the same source as logic and rationality itself. Since then we have significantly broadened our ideas of mathematics - and for the matter, of logic and rationality as well. This is what @fdrake is getting at: the more interesting questions in the philosophy of mathematics revolve around the rules themselves, rather than the uncontroversial fact that conclusions can be deduced by following those rules. -
 Zuhair
132to me axioms are just a medium in which consequential truths are harvested. Yet definitely in mathematical practice the axiomatics develop by capturing some concept, which fits the reciprocity part you've mentioned, and they are refined to suit basic intuitive grasps about those concepts at informal level, that way those axiomatic would be a kind of applied mathematics to those concepts, it provides analysis of those concepts. But all the systems born in that try (even the removed ones) are equally mathematical as far as they are media in which consequences are derived, that many times the original motivating concept is no longer the sole meaning attached to that system, and the line of development of those systems can ramify to capture different kinds of meaning quite different from the original meaning and so on.. Again the reality of those concepts are not the job of mathematics, it is the consequential load in those rule following games that is mathematics. I already alluded to that part of mathematical investigation in my last passage when I spoke about heuristics in finding the primary rules (axioms, inference rules, etc..) and suitable definitions and proof argument within those rule following games, and that part is, at many times, not directly trace-able to the primary rules themselves, but yet they are finally about consequences in those games, that part of mathematics is related to the ingenuity of mathematicians, but whatever it is, it finally aims to establishing an edifice in which consequential truths are harvested. They are creative acts that aims to enable consequential reasoning themes (games).
Zuhair
132to me axioms are just a medium in which consequential truths are harvested. Yet definitely in mathematical practice the axiomatics develop by capturing some concept, which fits the reciprocity part you've mentioned, and they are refined to suit basic intuitive grasps about those concepts at informal level, that way those axiomatic would be a kind of applied mathematics to those concepts, it provides analysis of those concepts. But all the systems born in that try (even the removed ones) are equally mathematical as far as they are media in which consequences are derived, that many times the original motivating concept is no longer the sole meaning attached to that system, and the line of development of those systems can ramify to capture different kinds of meaning quite different from the original meaning and so on.. Again the reality of those concepts are not the job of mathematics, it is the consequential load in those rule following games that is mathematics. I already alluded to that part of mathematical investigation in my last passage when I spoke about heuristics in finding the primary rules (axioms, inference rules, etc..) and suitable definitions and proof argument within those rule following games, and that part is, at many times, not directly trace-able to the primary rules themselves, but yet they are finally about consequences in those games, that part of mathematics is related to the ingenuity of mathematicians, but whatever it is, it finally aims to establishing an edifice in which consequential truths are harvested. They are creative acts that aims to enable consequential reasoning themes (games). -
 Zuhair
132I've already explicitly stated in my head post that I don't agree with formalism, mathematics is not limited to empty symbols rule following games, (usually called as string manipulation rules). Mathematics can involve meaning as far as those meanings are presented in a rule following manner, and this way it can provide analysis of those meaning, i.e. it can serve the application of concept analysis. But even then, the mathematics doesn't rely in those meanings, it lies in the consequential inferences those "meaning rule following games" derive, it is about how those meanings would be steamed by those rule following games. The nature of the concepts themselves is ought not to be a part of mathematics per se, it might be a part of philosophy of mathematics, but definitely it is not mathematics itself. Mathematics is just about consequential streaming scenarios, whether of meanings or of symbols.
Zuhair
132I've already explicitly stated in my head post that I don't agree with formalism, mathematics is not limited to empty symbols rule following games, (usually called as string manipulation rules). Mathematics can involve meaning as far as those meanings are presented in a rule following manner, and this way it can provide analysis of those meaning, i.e. it can serve the application of concept analysis. But even then, the mathematics doesn't rely in those meanings, it lies in the consequential inferences those "meaning rule following games" derive, it is about how those meanings would be steamed by those rule following games. The nature of the concepts themselves is ought not to be a part of mathematics per se, it might be a part of philosophy of mathematics, but definitely it is not mathematics itself. Mathematics is just about consequential streaming scenarios, whether of meanings or of symbols. -
 Wittgenstein
442
Wittgenstein
442
I hope that you won't mind my questions as l am confused by your term, " consequential truth ".
.
T+con(N) would rule out any statements like " this is not provable " and so on. Other than that, what will be a consequential truth of T itself and how does it differ from consequential truth of T+con(N) as a S that is a logical truth in T should also be a logical truth in T+con(N) .In other words S is provable in T+Con(N), that's why its said to be a logical truth, in reality it means that it is a consequential truth from the rule following game T+Con(N), notice that it is not a consequential truth of T itself. "Logical truth" is provability in some system
I will address your other points to but l need to get my head clear on these terms -
 Zuhair
132what I wanted to say is that "logical truth" is a relative concept, when you say that a statement s is logically true, I'll respond by saying "in relation to which system?", there is no absolute logical truth, it is always a consequence of some rule following game. Now back to Godel's sentence "G". Lets say we have a theory (a rule following game) T, now Godel demonstrated that there is a sentence "G^T" that corresponds to "G^T is not provable in T", now this sentence G^T is NOT a logical truth in T, because it is not a consequence of the rules of T, but it is a logical truth of T+Con(T). Of course any sentence s if it is a logical truth in T then it is a logical truth T+Con(T), but the opposite doesn't follow, you can have a sentence s that is a logical truth in T+Con(T), but it is not a logical truth in T, and Godel's sentence G^T is an example of such a sentence. What I wanted to say is that logical truth is "consequential truth" or you can call it "provability", so a logical truth in T is exactly what's provable in T. You cannot show a sentence that is a logical truth in T that is not provable in T, that's a contradiction, but you can show a sentence that is a logical truth in T+Con(T) that is not provable in T, because simply T+Con(T) is ANOTHER rule following game that is different from just T.
Zuhair
132what I wanted to say is that "logical truth" is a relative concept, when you say that a statement s is logically true, I'll respond by saying "in relation to which system?", there is no absolute logical truth, it is always a consequence of some rule following game. Now back to Godel's sentence "G". Lets say we have a theory (a rule following game) T, now Godel demonstrated that there is a sentence "G^T" that corresponds to "G^T is not provable in T", now this sentence G^T is NOT a logical truth in T, because it is not a consequence of the rules of T, but it is a logical truth of T+Con(T). Of course any sentence s if it is a logical truth in T then it is a logical truth T+Con(T), but the opposite doesn't follow, you can have a sentence s that is a logical truth in T+Con(T), but it is not a logical truth in T, and Godel's sentence G^T is an example of such a sentence. What I wanted to say is that logical truth is "consequential truth" or you can call it "provability", so a logical truth in T is exactly what's provable in T. You cannot show a sentence that is a logical truth in T that is not provable in T, that's a contradiction, but you can show a sentence that is a logical truth in T+Con(T) that is not provable in T, because simply T+Con(T) is ANOTHER rule following game that is different from just T. -
 fishfry
3.4kSo mathematics is about studying rule following games. — Zuhair
fishfry
3.4kSo mathematics is about studying rule following games. — Zuhair
https://en.wikipedia.org/wiki/Formalism_(philosophy_of_mathematics)
https://plato.stanford.edu/entries/formalism-mathematics/
I've already explicitly stated in my head post that I don't agree with formalism, — Zuhair
Hmmm. What does "mathematics is about rule following games" mean then? -
 Zuhair
132Formalism is the point of view that mathematics is about Non-meaningful rule following games. More precisely put: mathematics is about string (of empty symbols,i.e. meaningless) manipulation rules While here mathematics is about rule following games which can involve meaning as part of those rules, so it is not necessarily about manipulating strings of empty symbols.
Zuhair
132Formalism is the point of view that mathematics is about Non-meaningful rule following games. More precisely put: mathematics is about string (of empty symbols,i.e. meaningless) manipulation rules While here mathematics is about rule following games which can involve meaning as part of those rules, so it is not necessarily about manipulating strings of empty symbols. -
 fishfry
3.4kOk so in formalism, we have string manipulation rules that have no inherent meaning. But someone can use them by interpreting them; that is, by assigning the symbols meaning.
fishfry
3.4kOk so in formalism, we have string manipulation rules that have no inherent meaning. But someone can use them by interpreting them; that is, by assigning the symbols meaning.
which can involve meaning as part of those rules, — Zuhair
What does that mean? How is meaning "part of those rules?" For example we can do basic arithmetic from the Peano axioms without assigning any meaning to the symbols, then we can balance our checkbooks or do number theory using those symbols. But it's still formalism. There's no meaning inherent to the symbols.
So what does it mean for meaning to be part of the rules? -
 alcontali
1.3kAgain the reality of those concepts are not the job of mathematics, it is the consequential load in those rule following games that is mathematics. — Zuhair
alcontali
1.3kAgain the reality of those concepts are not the job of mathematics, it is the consequential load in those rule following games that is mathematics. — Zuhair
Totally agreed.
There is even an interesting paragraph on this principle in Wikipedia:
A philosophical defeat in the quest for "truth" in the choice of axioms
(Note: I personally consider it to be a victory.)
For good measure, and in order to stamp out the constructivist heresies that keep flying around, I propose to dig up and resurrect Luitzen Brouwer's dead body and to ritually kill him again. The problem is that Satan never dies completely; and unfortunately, neither does his notorious accomplice, Luitzen Brouwer, the worst constructivist heresiarch in the history of mankind. -
 Zuhair
132take any of lets say the meaningless rule following games. Add a rule that assigns to each symbol in that game a "particular meaning", this is a rule! Right? so it can be one of the rules in a rule following game, call it a meaning assignment rule. For example assign to the extra-logical symbols in the language of geometry some particular spatial concept, like for example a point being a kind of region in space, or being an atom in space, etc.., and then run the whole game of geometry in connection with this particular meaning. By then the result is a meaningful rule following game. This is a legitimate rule following game, but it incorporates meaning within it. Of course you can strip away the meaning by removing the meaning assignment rules, and you get the bare empty symbol rule manipulating game, OK, but that's ANOTHER game.This kind of games (the meaningful ones) is important in concept analysis, and in applied mathematics in general. For example applied mathematics in physics, can only be played in a meaningful manner, same in chemistry, ethics, etc... those are usually only played with meanings incorporated within them. Even arithmetic can be played in mind with some meaning incorporated to its symbols like for example of naturals being indices of the quantity of elements in finite sets, of summation being the indices of disjoint unions of indexed sets, etc.. this makes playing those games easier form the human side. But as you said they are not indispensable, you can dispense with any such connotation and proceed in a meaningless manner like a machine. No problem.
Zuhair
132take any of lets say the meaningless rule following games. Add a rule that assigns to each symbol in that game a "particular meaning", this is a rule! Right? so it can be one of the rules in a rule following game, call it a meaning assignment rule. For example assign to the extra-logical symbols in the language of geometry some particular spatial concept, like for example a point being a kind of region in space, or being an atom in space, etc.., and then run the whole game of geometry in connection with this particular meaning. By then the result is a meaningful rule following game. This is a legitimate rule following game, but it incorporates meaning within it. Of course you can strip away the meaning by removing the meaning assignment rules, and you get the bare empty symbol rule manipulating game, OK, but that's ANOTHER game.This kind of games (the meaningful ones) is important in concept analysis, and in applied mathematics in general. For example applied mathematics in physics, can only be played in a meaningful manner, same in chemistry, ethics, etc... those are usually only played with meanings incorporated within them. Even arithmetic can be played in mind with some meaning incorporated to its symbols like for example of naturals being indices of the quantity of elements in finite sets, of summation being the indices of disjoint unions of indexed sets, etc.. this makes playing those games easier form the human side. But as you said they are not indispensable, you can dispense with any such connotation and proceed in a meaningless manner like a machine. No problem.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum







