-
 alcontali
1.3kTherefore we cannot prove a statement that cannot be proven in this axiomatic system is semantically true, and to the extent of our logical method, this new axiomatic system can never be proven incomplete. — simeonz
alcontali
1.3kTherefore we cannot prove a statement that cannot be proven in this axiomatic system is semantically true, and to the extent of our logical method, this new axiomatic system can never be proven incomplete. — simeonz
I think that there are two remarks that are possibly relevant in this context.
First. These "true but unprovable" statements will appear to use as simply undecidable. Indeed, how are we even going to decide that they are "true", if we cannot possibly prove the statement nor disprove its opposite? Hence, the practical qualification will not be "true but unprovable" but "undecidable".
Second. Number theory (by default: Dedekind-Peano) is a sub-theory of set theory (by default: ZFC), meaning that every number-theoretical theorem can be proven in set theory, but not the other way around. Now, there really are number-theoretical theorems that are fundamentally undecidable in number theory (=DP), but provable in the larger set theory (=ZFC):
Undecidable statements provable in larger systems
These are natural mathematical equivalents of the Gödel "true but undecidable" sentence. They can be proved in a larger system which is generally accepted as a valid form of reasoning, but are undecidable in a more limited system such as Peano Arithmetic.
In 1977, Paris and Harrington proved that the Paris–Harrington principle, a version of the infinite Ramsey theorem, is undecidable in (first-order) Peano arithmetic, but can be proved in the stronger system of second-order arithmetic. Kirby and Paris later showed that Goodstein's theorem, a statement about sequences of natural numbers somewhat simpler than the Paris–Harrington principle, is also undecidable in Peano arithmetic.
Kruskal's tree theorem, which has applications in computer science, is also undecidable from Peano arithmetic but provable in set theory. In fact Kruskal's tree theorem (or its finite form) is undecidable in a much stronger system codifying the principles acceptable based on a philosophy of mathematics called predicativism. The related but more general graph minor theorem (2003) has consequences for computational complexity theory.
Now, we may not have fundamentally stronger theories than set theory (=ZFC). In other words, there may not be such larger theory of which set theory would just be a sub-theory. Therefore, when a theorem is undecidable in set theory, it may even be absolutely undecidable. One reason why we may not go higher nor further than ZFC, is because ZFC is already at the level of Turing-completeness -- can compute everything that is computable and therefore: can represent all knowledge that can be expressed in language. ZFC is possibly even stronger than that:
What is the relationship between ZFC and Turing machine?
In the other direction, a universal Turing machine can be encoded in ZFC, indeed in far weaker theories, such as relatively small fragments of number theory.
...
Suppose, for reductio, that a Turing machine could decide whether the sentence with Gödel number n
is a theorem of ZFC ... Now, by the diagonalization lemma, there would be a Gödel-style sentence γ such that ... Contradiction is immediate. [meaning: ZFC is stronger than Turing-complete]
On the other hand, Turing Completeness is already a seriously constraining limit:
All known laws of physics have consequences that are computable by a series of approximations on a digital computer. A hypothesis called digital physics states that this is no accident because the universe itself is computable on a universal Turing machine. This would imply that no computer more powerful than a universal Turing machine can be built physically.
This does not mean that there are no attempts at increasing the strength of ZFC by adding new axioms. The web is plastered with such attempts.
Still, successfully arguing that a new axiom is independent of the ten existing axioms in ZFC is a non-trivial job, given the strength of ZFC. After that, they still need to successfully prove from this extended system, a theorem that is provably undecidable in ZFC, such as for example the Continuum Hypothesis. That job is certainly not easy ... -
 simeonz
310
simeonz
310
Thanks for the response. I'm sorry I couldn't respond earlier.
I couldn't express myself properly, but this is what I meant. I was attempting to construct an axiomatic system, whose undecidable sentences are not amenable to further evaluation by means of metalogic. The idea was to start with incomplete axiomatic system and to import proofs of undecidable statements by continuously adding meta-axioms. There were problems with this approach.These "true but unprovable" statements will appear to use as simply undecidable. — alcontali
If I understand you correctly, there are axiomatic systems which preserve the truth values of all statements of Peano arithmetic, but make previously undecidable statements decidable? It is a curious fact. So, we don't actually have an axiomatic system yet, in which all statements of Peano arithmetic are decidable?Number theory (by default: Dedekind-Peano) is a sub-theory of set theory (by default: ZFC), meaning that every number-theoretical theorem can be proven in set theory, but not the other way around. Now, there really are number-theoretical theorems that are fundamentally undecidable in number theory (=DP), but provable in the larger set theory (=ZFC): — alcontali
Just thinking out loud, I wonder whether we would know if ZFC is semantically complete or not, if it were deductively incomplete? And what would be our course of action if we can't know? And on a related note, I wonder whether a theorem with the same quality as Chaitin's constant for Turing machines can be discovered for ZFC - having definite truth value, but no proof in logic or meta-logic.Now, we may not have fundamentally stronger theories than set theory (=ZFC). In other words, there may not be such larger theory of which set theory would just be a sub-theory. Therefore, when a theorem is undecidable in set theory, it may even be absolutely undecidable. — alcontali
Yes, I think that it is also intuitive that ZFC cannot be weaker than a universal Turing machine. I also thought that it cannot be stronger. Since non-deterministic Turing machines are computationally equivalent to their deterministic counterpart and should be able to simulate successfully any deductive system. I mean - that was my intuition anyhow.One reason why we may not go higher nor further than ZFC, is because ZFC is already at the level of Turing-completeness -- can compute everything that is computable and therefore: can represent all knowledge that can be expressed in language. ZFC is possibly even stronger than that — alcontali
I have wondered about this. I am not intimately familiar with the hypothesis, but it becomes ever more so obvious that material and abstract sciences are intertwined together. There are some implicit assumptions here, like discrete finite state and determinism. If I recall correctly non-determinism cannot produce more computability. But it can produce more outcomes, and I cannot tell whether this can contribute to nature somehow. Analog or infinite state may be unfeasible, as per QM. The hypothesis does depend on a number of assumptions, but may be true nonetheless.On the other hand, Turing Completeness is already a seriously constraining limit:
All known laws of physics have consequences that are computable by a series of approximations on a digital computer. A hypothesis called digital physics states that this is no accident because the universe itself is computable on a universal Turing machine. This would imply that no computer more powerful than a universal Turing machine can be built physically. — alcontali
Thanks again for the response. It is thought provoking. -
 alcontali
1.3kIf I understand you correctly, there are axiomatic systems which preserve the truth values of all statements of Peano arithmetic, but make previously undecidable statements decidable? — simeonz
alcontali
1.3kIf I understand you correctly, there are axiomatic systems which preserve the truth values of all statements of Peano arithmetic, but make previously undecidable statements decidable? — simeonz
By the way, there is a problem with the terminology. Decidability is about computability:
Decidability should not be confused with completeness. For example, the theory of algebraically closed fields is decidable but incomplete, whereas the set of all true first-order statements about nonnegative integers in the language with + and × is complete but undecidable. Unfortunately, as a terminological ambiguity, the term "undecidable statement" is sometimes used as a synonym for independent statement.
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is proved to be impossible to construct an algorithm that always leads to a correct yes-or-no answer.
While independence is about provability:
In mathematical logic, independence is the unprovability of a sentence from other sentences. A sentence σ is independent of a given first-order theory T if T neither proves nor refutes σ; that is, it is impossible to prove σ from T, and it is also impossible to prove from T that σ is false. Sometimes, σ is said (synonymously) to be undecidable from T; this is not the same meaning of "decidability" as in a decision problem.
There seems to be a preference to use the term "independent" (mathematics) instead of "undecidable" (computer science) for "unprovability" of the statement or its negation. The problem is caused by the fact that these terms emerged from two different domains, but are very related. Given the Curry-Howard Correspondence, undecidability and independence overlap much stronger than suggested by these commentators:
In programming language theory and proof theory, the Curry–Howard correspondence (also known as the Curry–Howard isomorphism or equivalence, or the proofs-as-programs and propositions- or formulae-as-types interpretation) is the direct relationship between computer programs and mathematical proofs.
The Curry–Howard correspondence is the observation that two families of seemingly unrelated formalisms—namely, the proof systems on one hand, and the models of computation on the other—are in fact the same kind of mathematical objects. If one abstracts on the peculiarities of either formalism, the following generalization arises: a proof is a program, and the formula it proves is the type for the program.
The difference between "undecidable" and "independent" seems to depend mostly "on the peculiarities of either formalism" rather than on truly fundamental issues.
The canonical example of a theorem not provable in Peano arithmetic but in ZFC is:
Kruskal's tree theorem, which has applications in computer science, is also undecidable from Peano arithmetic but provable in set theory.
In fact, the commentators below argue that this does not mean that ZFC is "stronger" than PA. The fact that ZFC accepts the theorem while PA doesn't, is rather a trust issue.
So, we don't actually have an axiomatic system yet, in which all statements of Peano arithmetic are decidable? — simeonz
I have found the following (formal) thought exercise on exactly this matter. The author calls such encompassing axiomatic system a "provability oracle for Peano arithmetic":
So having a provability oracle for PA or any other consistent formal system that proves some valid arithmetic truths (like ZFC) is equivalent to having a halting oracle, and thus leads to a provability oracle for any other formal system. In other words, if you knew all about the logical implications of PA, then you would also know all about the logical implications of ZFC and all other formal systems. Hee hee.
PA can see everybody else's theorems as Gödel numbers. So, it actually "knows" everything what these other systems know.
Then, I found the following intriguing remark as a comment to the article on the provability oracle for PA:
More powerful formal systems are not more powerful because they know more stuff. They're more powerful because they have more confidence. PA proves that PA+Con(PA) proves Con(PA) (the proof, presumably, is not very long), but PA does not trust PA+Con(PA) to be accurate. ZFC is even more confident - has even fewer models - and so is even stronger. (Maybe it even has no models!)
ZFC is not more powerful than PA because it knows more stuff. In fact, that would not be possible. Such theorem (as well as its proof) would still be a Gödel number which PA can also reach. Therefore, PA actually "knows" all possible theorems (and their proofs) that can be expressed in language. Therefore, it also knows all the axioms and all theorems (including their proofs) of all the other systems. The problem is that PA does not "trust" them.
Therefore, ZFC does not "know" more than PA. It just trusts more. In some ways, that is not really "stronger" or "more powerful". It could just be that ZFC is more gullible. -
 simeonz
310
simeonz
310
I think I understand the nuance. There are undecidable deductively complete theories, so claiming that an undecidable statement makes a theory deductively incomplete sounds strange. Saying that the statement is independent from the axioms, purely as a vocabulary, reduces the confusion.By the way, there is a problem with the terminology. Decidability is about computability:
...
While independence is about provability:
...
The difference between "undecidable" and "independent" seems to depend mostly "on the peculiarities of either formalism" rather than on truly fundamental issues. — alcontali
I will also confess - I realized what profound misunderstanding of Gödel's semantic incompleteness I had. I believed that the theorem states that a valid (i.e. true in every model) statement can be independent from the axioms, which indeed would be exciting. Instead, it only states that a satisfiable statement can be independent. (Edit: And that such statement always exists for powerful enough theories.) The Gödel completeness theorem actually states the contrary to my prior understanding. That for first-order theories, validity and provability are the same. What a terrible confusion on my end. :)
Which makes me wonder. Since the semantic incompleteness proof holds for the standard model, what is the "intended" interpretation for other theories. Is there a criterion for a model being standard in general. For example, in denotational semantics of programming languages, a minimal interpretation is the least fixed point of a certain interpretation operator. I wonder, whether this has analogy for model theory. Such as, by using the compactness theorem and gradually building the interpretation domain, by arriving at domain entities using Skolemization or something.
I also couldn't clear up if ZFC is decidable, undecidable, or not yet established. Wikipedia indicates that there are only decidable sublanguages, while a stackexchange answer indicates that ZFC is recursively enumerable, which if mu-recursively enumerable, should mean that ZFC is decidable by Turing machines.
I find the Curry-Howard Correspondence a little strange. I'm sure it makes sense, but likening axioms to a pre-execution invariant and theorems to a post-execution invariant appears complicated. It may have something to do with formal verification processes, but for me, the relationship between proofs and computation appears to be about enumeration of proofs by turing machines in one direction, and the generation of booleans on the Turing tape for the proven theorems after every inference step in the other direction.Given the Curry-Howard Correspondence, undecidability and independence overlap much stronger than suggested — alcontali
After clearing up my error in understanding, hopefully, I am not very surprised. Indeed, because of Gödel's completeness theorem, if a theory were able to prove a statement of PA that PA iteself couldn't, it would have fewer models. The stronger theory would not simply be deductively stronger, but semantically stronger. I was mistakenly excited that a theory with equivalent semantics (one that is expansion of PA) could cure PA's incompleteness. I was hoping that because the new axioms are not statements of PA itself, but their interpretations, they might result in some completely different configuration, without restricting the model space. But this is apparently not the case, at least for first-order logic.ZFC is not more powerful than PA because it knows more stuff. In fact, that would not be possible. Such theorem (as well as its proof) would still be a Gödel number which PA can also reach. Therefore, PA actually "knows" all possible theorems (and their proofs) that can be expressed in language. Therefore, it also knows all the axioms and all theorems (including their proofs) of all the other systems. The problem is that PA does not "trust" them. — alcontali
Edit: correction about Gödel's completeness theorem - I used the term unsatisfiability, where I wanted to say not being valid or unsatisfiable (corrected now) -
 alcontali
1.3kI also couldn't clear up if ZFC is decidable, undecidable, or not yet established. Wikipedia indicates that there are only decidable sublanguages, while a stackexchange answer indicates that ZFC is recursively enumerable, which if mu-recursively enumerable, should mean that ZFC is decidable by Turing machines. — simeonz
alcontali
1.3kI also couldn't clear up if ZFC is decidable, undecidable, or not yet established. Wikipedia indicates that there are only decidable sublanguages, while a stackexchange answer indicates that ZFC is recursively enumerable, which if mu-recursively enumerable, should mean that ZFC is decidable by Turing machines. — simeonz
ZFC is subject to the diagonal lemma, and therefore is syntactically incomplete. Hence, it must necessarily have undecidable statements that can be expressed in first-order logic.
Since the semantic incompleteness proof holds for the standard model, what is the "intended" interpretation for other theories. — simeonz
Every legitimate answer that is true, has a proof (semantic completeness), but there exist legitimate questions for which an answer cannot be determined (syntactic incompleteness).
Concerning the implications of Gödel's semantic completeness theorem for other systems than Peano arithmetic, we are talking about advanced model theory, which is an enormous subject in itself. I am not sure about the answer, really. I have never looked into it.
I find the Curry-Howard Correspondence a little strange. I'm sure it makes sense, but likening axioms to a pre-execution invariant and theorems to a post-execution invariant appears complicated. It may have something to do with formal verification processes, but for me, the relationship between proofs and computation appears to be about enumeration of proofs by turing machines in one direction, and the generation of booleans on the Turing tape for the proven theorems after every inference step in the other direction. — simeonz
In 1958 [Curry] observes that a certain kind of proof system, referred to as Hilbert-style deduction systems, coincides on some fragment to the typed fragment of a standard model of computation known as combinatory logic.[4]
In order to illustrate this understanding, it is clearly a question of producing good examples of Hilbert calculi as well as good examples of combinator calculi, along with an argument that maps an example in one formalism to an example in the other. It is a lot of work, but it should allow to develop a deeper understanding of the nitty-gritty details of what exactly Curry meant to say.
It is interesting to work on such explanation by examples, but then again, who else would be interested in reading the results? This discussion on the diagonal lemma is probably already more than what many potential readers would want to handle ... -
 simeonz
310
simeonz
310
My understanding from the definition was that for a theory to be decidable, it is necessary to have effective enumeration of its theorems, not to have a theorem for every statement or its negation. In that sense, I thought, whether ZFC is decidable is a separate subject matter from its syntactical incompleteness.ZFC is subject to the diagonal lemma, and therefore is syntactically incomplete. Hence, it must necessarily have undecidable statements that can be expressed in first-order logic. — alcontali
I understand, but just to clarify. I wasn't so much curious about Gödel's semantic completeness directly as application with respect to other axiomatic systems, i.e. examples of models that satisfy a statement that is independent of the axioms. I was wondering whether there exists a definition of some kind of "minimal" class of models for every theory. Because, as it stands, I am under the impression that semantic incompleteness says nothing that the syntactic incompleteness and semantic completeness theorems together don't say. If such models were defined and coincided with our "intuitive" definition of interpretation of a theory (similarly to what denotational semantics offers for recursive programs), and Gödel's semantic incompleteness were shown to apply to such models (i.e. they always satisfied a statement that cannot be derived from the axioms), it would make the claim stand on its own.Concerning the implications of Gödel's semantic completeness theorem for other systems than Peano arithmetic, we are talking about advanced model theory, which is an enormous subject in itself. — alcontali
Absolutely. I will look into it on my own when I have the time. Logic is a past time interest for me, so I have gaps in my understanding at the moment. But I am trying to cure them, a piece at a time.It is interesting to work on such explanation by examples, but then again, who else would be interested in reading the results? This discussion on the diagonal lemma is probably already more than what many potential readers would want to handle ... — alcontali
Thanks for the responses. -
 alcontali
1.3kMy understanding from the definition was that for a theory to be decidable, it is necessary to have effective enumeration of its theorems, not to have a theorem for every statement or its negation. — simeonz
alcontali
1.3kMy understanding from the definition was that for a theory to be decidable, it is necessary to have effective enumeration of its theorems, not to have a theorem for every statement or its negation. — simeonz
Effective axiomatization. A formal system is said to be effectively axiomatized (also called effectively generated) if its set of theorems is a recursively enumerable set (Franzén 2005, p. 112).This means that there is a computer program that, in principle, could enumerate all the theorems of the system without listing any statements that are not theorems. Examples of effectively generated theories include Peano arithmetic and Zermelo–Fraenkel set theory (ZFC).
Completeness. A set of axioms is (syntactically, or negation-) complete if, for any statement in the axioms' language, that statement or its negation is provable from the axioms (Smith 2007, p. 24).
The issue of syntactic completeness only arises in theories that have effective enumeration of its theorems:
The first incompleteness theorem states that no consistent system of axioms whose theorems can be listed by an effective procedure (i.e., an algorithm) is capable of proving all truths about the arithmetic of natural numbers. For any such consistent formal system, there will always be statements about natural numbers that are true, but that are unprovable within the system.
Hence, only theories with effective axiomatization can possibly be incomplete. Other theories are not even being considered in this context. -
 simeonz
310I am not intimately familiar with the subject, but I think there is some issue with the Wikipedia article.
simeonz
310I am not intimately familiar with the subject, but I think there is some issue with the Wikipedia article.
There also may be linguistical confusion again. Many internet sources quote undecidability of PA, talking about sentences of PA's language that cannot be evaluated. The point is - sentences of the underlying language, not theorems of the theory, which implies that particular model semantics are involved. Otherwise, sentences that are not theorems (edit: themselves or their negations) don't have definite truth value in first-order theory, as per the completeness theorem. The wikipedia definition of decidability clearly talks about theorems only:
A theory (set of sentences closed under logical consequence) in a fixed logical system is decidable if there is an effective method for determining whether arbitrary formulas are included in the theory. — Wikipedia
Further in the decidability article, it is clearly stated:
Decidability should not be confused with completeness. For example, the theory of algebraically closed fields is decidable but incomplete, whereas the set of all true first-order statements about nonnegative integers in the language with + and × is complete but undecidable. — Wikipedia
Thus neither property implies the other. I should mention that I did confuse the issue somewhat, because recursive enumerability (i.e. effective axiomatization, semidecidability) is actually a weaker property, which does not answer negatively for statements not in the theory. Actual decidability requires negative and positive determination by effective method. Semidecidability is defined later in the same article. Even so, however, decidable, but incomplete theories, are also semidecidable, but incomplete ones. Thus, the statement holds that semidecidability does not imply completeness.
Edit: From reading on the web, I see that there is an important caveat. Every recursively enumerably axiomatizable theory is recursively enumerable. And every recursively enumerable syntactically complete theory is decidable. A complete theory may be undecidable, but for "sensible" theories (with effective axiomatization), completeness does imply decidability. So, as you stated, if ZFC were complete it would be decidable. But since it is not, does my original question - if it is decidable or not still stand? (That is, considering that it is effectively axiomatized, if that matters.)
From the definition you quoted, a complete axiomatic theory has a proof for either the statement or its negation. That does not mean that all such proofs or statements can be enumerated by a single effective procedure simultaneously. (PS. According to the previous edit I made, the answer is yes, for the more conventionally axiomatized theories.)Completeness. A set of axioms is (syntactically, or negation-) complete if, for any statement in the axioms' language, that statement or its negation is provable from the axioms (Smith 2007, p. 24). — alcontali
The summary of Gödel's first incompleteness theorem in the introduction to the Wikipedia article (which you quoted) seems to talk about validity ("capable of proving all truths"), which is not trademark of the first theorem, but the second one. And the account differs from the formulation in the body of the article:
I reason, that for a statement to lack proof implies that it is not part of the axiomatization consequences. Not that it is part of the axiomatization consequences, but those cosequences cannot be computed.First Incompleteness Theorem: "Any consistent formal system F within which a certain amount of elementary arithmetic can be carried out is incomplete; i.e., there are statements of the language of F which can neither be proved nor disproved in F." (Raatikainen 2015) — Wikipedia
Edit: Although, it appears that the theorem have been formulated for primitively recursively enumerable axiomatization originally. (According to this stackexchange remark.) According to the summary of one article I found, it appears to admit extension to non-enumerable theories.
And further in the article:
This contradicts the summary, by clearly stating that validity is not the subject of the theorem. And finally, the following paragraph shows that the Gödel sentence is merely satisfiable in the standard model, not in every model:The first incompleteness theorem shows that the Gödel sentence GF of an appropriate formal theory F is unprovable in F. Because, when interpreted as a statement about arithmetic, this unprovability is exactly what the sentence (indirectly) asserts, the Gödel sentence is, in fact, true (Smoryński 1977 p. 825; also see Franzén 2005 pp. 28–33). For this reason, the sentence GF is often said to be "true but unprovable." (Raatikainen 2015). However, since the Gödel sentence cannot itself formally specify its intended interpretation, the truth of the sentence GF may only be arrived at via a meta-analysis from outside the system. — Wikipedia
Although the Gödel sentence of a consistent theory is true as a statement about the intended interpretation of arithmetic, the Gödel sentence will be false in some nonstandard models of arithmetic, as a consequence of Gödel's completeness theorem (Franzén 2005, p. 135). — Wikipedia
Talking about the relationship between syntactic completeness and decidability, I think that there is some definitional ambiguity again. I think that it is sometimes meant to imply a procedure for evaluating (assigning truth value) to all sentences of the language of the theory (which requires syntactic completeness), or procedure that enumerates all statements satisfiable by the standard model (which isn't actually semantic completeness, because all first-order theories are semantically complete, but completeness with respect to a model). -
 alcontali
1.3kSo, as you stated, if ZFC were complete it would be decidable. But since it is not, does my original question - if it is decidable or not still stand? — simeonz
alcontali
1.3kSo, as you stated, if ZFC were complete it would be decidable. But since it is not, does my original question - if it is decidable or not still stand? — simeonz
I suspect that ZFC is not decidable, but then again, it really depends on the link between completeness and decidability. If there exists a procedure to solve the proof problem, the proof problem is decidable. That means that the theorem is provable from the theory. In that sense, provability is a decidability problem, because a proof is a procedure.
However, since the Gödel sentence cannot itself formally specify its intended interpretation, the truth of the sentence GF may only be arrived at via a meta-analysis from outside the system. — Wikipedia
That is actually what they do in the Wikipedia page.
This contradicts the summary, by clearly stating that validity is not the subject of the theorem. — simeonz
I think that it is the semantic completeness theorem that throws a spanner in the works: For a statement deemed true by the system, some proof must exist within the system. Therefore, the result would be contradictory, unless the truth of the Gödel sentence is evaluated outside the system. In my impression, the Gödel sentence is true in the metasystem but not provable in the system itself. One of the difficulties in this matter is that some reasoning takes place within the system, and some about the system, from outside the system. -
 simeonz
310
simeonz
310
I see. Thinking about it, semidecidability I imagine will carry a lot of practical utility for applications like automated theorem proving, even though it doesn't guarantee termination. Decidability is probably more crucial to theoretic analysis.I suspect that ZFC is not decidable, but then again, it really depends on the link between completeness and decidability. If there exists a procedure to solve the proof problem, the proof problem is decidable. That means that the theorem is provable from the theory. In that sense, provability is a decidability problem, because a proof is a procedure. — alcontali
I actually don't know how the syntactic incompleteness was proven (through the same meta-logical argument as its semantic counterpart or not), but it seems that you shouldn't need a lot of semantics in order to demonstrate that some statement is independent. If the statement's derivation involves circularity (like the Gödel sentence), it should be entirely a deductive property if this circularity can be eliminated or not. But I might be wrong.I think that it is the semantic completeness theorem that throws a spanner in the works: For a statement deemed true by the system, some proof must exist within the system. — alcontali -
 alcontali
1.3kI actually don't know how the syntactic incompleteness was proven (through the same meta-logical argument as its semantic counterpart or not), but it seems that you shouldn't need a lot of semantics in order to demonstrate that some statement is independent. If the statement's derivation involves circularity (like the Gödel sentence), it should be entirely a deductive property if this circularity can be eliminated or not. But I might be wrong. — simeonz
alcontali
1.3kI actually don't know how the syntactic incompleteness was proven (through the same meta-logical argument as its semantic counterpart or not), but it seems that you shouldn't need a lot of semantics in order to demonstrate that some statement is independent. If the statement's derivation involves circularity (like the Gödel sentence), it should be entirely a deductive property if this circularity can be eliminated or not. But I might be wrong. — simeonz
I am not familiar enough with Gödel's semantic completeness theorem. The explanation does not contain elaborate examples to illustrate the details of what they are talking about. It would be quite a job to inject examples in the right places.
For example:
But the ring Z of integers, which is not a field, is also a σf-structure in the same way. In fact, there is no requirement that any of the field axioms hold in a σf-structure.
A ring is "almost" a field -- it just lacks inverses (it is not closed under division) -- but that's the little I understand of why this ring is still a model (=σf-structure) of a field ... I hope that Wikipedia will manage to better elaborate on this subject. -
 simeonz
310
simeonz
310
I am not familiar either, considering that I didn't understand its significance before yesterday. But from what I understand, it essentially states that inference and semantics are equivalent in a first order theory. If the theory knows something, it is true in all models (i.e. true for all interpretations consistent with the axioms), and if something is true in all models, the theory knows it. I don't find this surprising, as it makes intuitive sense. What I find more surprising is that it doesn't hold for higher order logics, as elaborated here:I am not familiar enough with Gödel's semantic completeness theorem. The explanation does not contain elaborate examples to illustrate the details of what they are talking about. It would be quite a job to inject examples in the right places. — alcontali
The completeness theorem is a central property of first-order logic that does not hold for all logics. Second-order logic, for example, does not have a completeness theorem for its standard semantics (but does have the completeness property for Henkin semantics), and the set of logically-valid formulas in second-order logic is not recursively enumerable. The same is true of all higher-order logics. It is possible to produce sound deductive systems for higher-order logics, but no such system can be complete. — Wikipedia
A ring is "almost" a field -- it just lacks inverses (it is not closed under division) -- but that's the little I understand of why this ring is still a model (=σf-structure) of a field ... I hope that Wikipedia will manage to better elaborate on this subject. — alcontaliActually, to my understanding, the signature is not a model, but the "embodied" part of the alphabet for the language of the theory - the rest being variables, quantifiers, logical symbols, are not specific or have no particular meaning. What the article states, if I read it correctly, is that the signature need not incorporate symbols, which taken as abstract mathematical objects, have semantics compatible with the models of the theory. This seems rather vacuous statement, considering that these are just symbols.
Edit: Thinking about it again, I probably overtrivialized the statement the article makes. It talks about the structure, not just the signature, which would include the interpretation and the domain as well. Considering their examples, you are right. And then indeed, it sounds a little non-sensical. But what they could mean is that an interpretation could assign 0 and 1 to their usual counterparts. And then addition, multiplication and inverses could map to relations that are subsets of Cartesian products of the integer set, but encode rationals using a pairing function. In other words, the article probably states that the function and relation symbols need not be mapped to their standard counterparts for the domain, but merely to functions and relations consistent with the theory. -
 bongo fury
1.8k
bongo fury
1.8k
Just in case pictures help anyone with the wiki proof.
Grateful for notification of errors, or suggestions for further signposting or clarification.
Single pdf here.
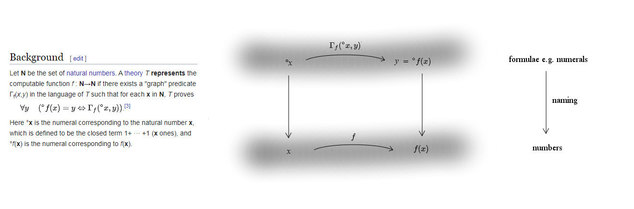
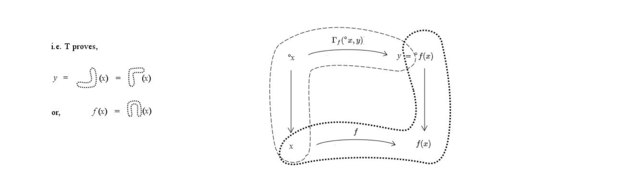
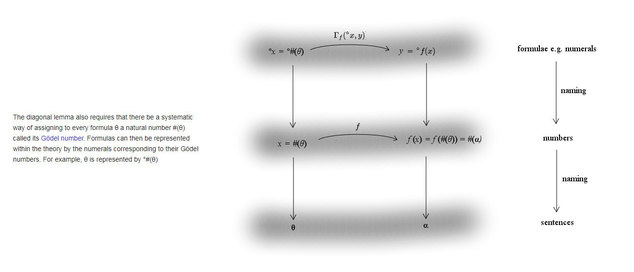
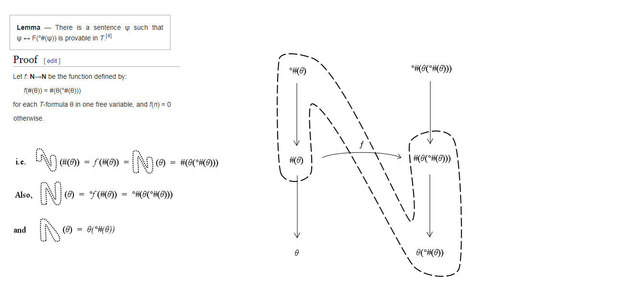
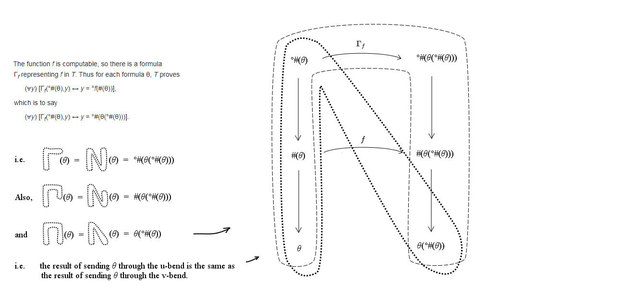
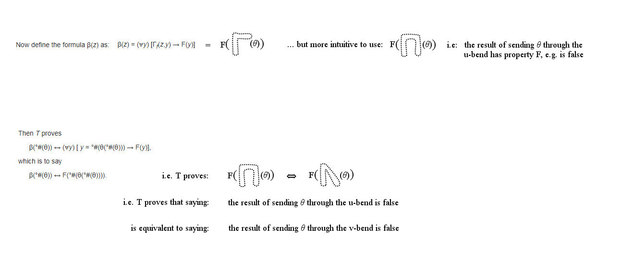
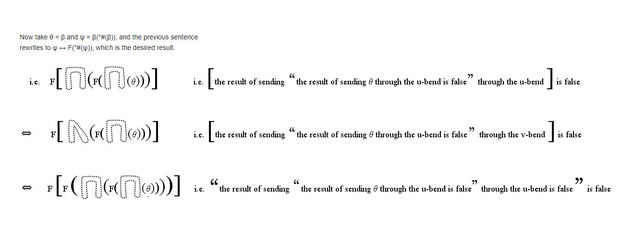
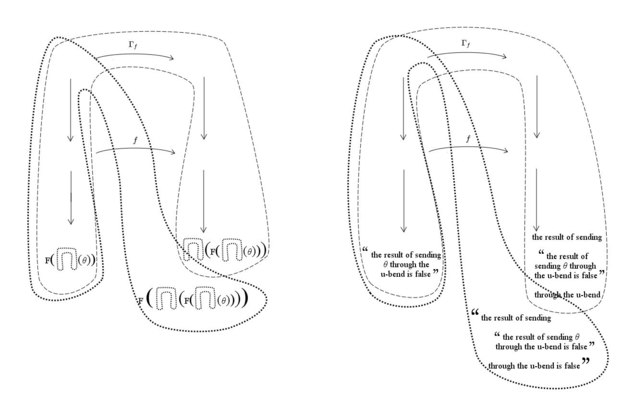
No toilet humour intended. :chin: -
 alcontali
1.3kJust in case pictures help anyone with the wiki proof, or are of interest. Grateful for notification of errors, or suggestions for further signposting or clarification. — bongo fury
alcontali
1.3kJust in case pictures help anyone with the wiki proof, or are of interest. Grateful for notification of errors, or suggestions for further signposting or clarification. — bongo fury
I think that the idea of "bends" is certainly useful in helping to understand the proof. However, I think that a video with animation would be very useful to illustrate it, i.e. a youtube video or so. In my opinion, the pdf does not provide enough explanation nor visual feedback about the bends, actually. -
 Andrew M
1.6kA belated thanks for your reply! I've spent some time working through the proof of the diagonal lemma and do have a few questions.
Andrew M
1.6kA belated thanks for your reply! I've spent some time working through the proof of the diagonal lemma and do have a few questions.
However I thought I'd first attempt my own ELI12 explanation of the diagonal lemma. Any critiques welcome.
Consider the following sentence:
- Simon says this sentence
That is an example of a sentence that refers to itself. What Simon purportedly says is the sentence itself and the predicate is Simon says. Notice that the sentence is always true when Simon says it and always false otherwise. If we name the sentence as S, we can express that result as:
- S is true if and only if Simon says S
Now suppose that the language we're considering doesn't support the word this (as is the case for certain formal languages). However it does support variables and substitutions. We can construct the sentence 'Simon says v' where v is a variable and have v be replaced by the entire quoted sentence. The result would be:
- Simon says 'Simon says v'
That substitution procedure is called diagonalization. But we have a problem. If Simon says the full sentence (meaning that it's true that Simon says "Simon says 'Simon says v'"), then what the sentence itself asserts is false (since Simon didn't just say "Simon says v"). The problem is that the inner and outer sentences express different ideas. But there is a solution. We can construct the sentence to instead refer to the result of the substitution procedure, i.e., 'Simon says the diagonalization of v'. Diagonalizing that sentence gives:
- Simon says the diagonalization of 'Simon says the diagonalization of v'
And now we're done! If Simon says the full sentence, then he is saying the diagonalization of the inner sentence. Which is just what the sentence itself asserts. So the full sentence is the fixed point of the predicate Simon says. It is true if and only if Simon says it. Naming the sentence as S2:
- S2 is true if and only if Simon says S2
Generalizing the above for any predicate (F) and sentence (X), we get:
- X ↔ F(X)
Which is the diagonal (fixed point) lemma. (Ignoring Godel numbering to keep it simple.)
From here it is a small step to Tarski's Undefinability Theorem and Godel's Incompleteness Theorems. Just replace the predicate F with IsNotTrue and IsNotProvable respectively and work through the implications. -
 Andrew M
1.6kReturning to this...
Andrew M
1.6kReturning to this...
The formal statement of Tarski's undefinability theorem is, of course, expressed in terms of the diagonal lemma:
That is, there is no L-formula True(n) such that for every L-formula A, True(g(A)) ↔ A holds.
So, there does not exist such number predicate True(%S) because there would always exist exceptions to the proposition that: S ↔ True(%S). That would render the entire theory inconsistent. — alcontali
Yes, in effect the diagonal lemma can generate the Liar sentence, as follows:
- This sentence is not true
Which, in turn, leads to contradiction in the system. However it raises the question as to what it is about the Liar sentence that makes it problematic. As I see it, the deeper reason is that it promises a sentence that can be evaluated as true or false. However instead of delivering on that promise, it merely returns the same sentence which makes the same promise (and therefore entails an endless cycle).
The Truth-Teller ("This sentence is true") is similar in that it also doesn't deliver a sentence that can be evaluated, merely the promise of one. While assuming it to be either true or false doesn't lead to any contradiction, that truth value is arbitrary. Again not particularly useful or informative.
Now consider the Godel sentence which is, in effect:
- This sentence is not provable
Unlike the Liar sentence, assuming the Godel sentence is true doesn't lead to contradiction. Whereas assuming the Godel sentence is false does lead to contradiction.
So the usual conclusion is to accept incompleteness - there is at least one sentence in the system that is true but unprovable. Though an alternative conclusion is that the system is complete but inconsistent.
However there is a third alternative. Specifically, the Godel sentence has the same problem as the Liar and Truth-Teller sentences. It promises to deliver a sentence that can be evaluated (such as "12 > 3" which is provable or conversely "12 < 3" which is not provable (or provably false)). But instead of delivering on that promise, it merely returns the same sentence which makes the same promise (and again entails an endless cycle).
The seemingly natural solution would be to exclude Provable(%S) as a primary predicate (as with True(%S), per Tarski) thus preventing the Godel sentence from being generated via the diagonal lemma. -
 alcontali
1.3kThe seemingly natural solution would be to exclude Provable(%S) as a primary predicate (as with True(%S), per Tarski) thus preventing the Godel sentence from being generated via the diagonal lemma. — Andrew M
alcontali
1.3kThe seemingly natural solution would be to exclude Provable(%S) as a primary predicate (as with True(%S), per Tarski) thus preventing the Godel sentence from being generated via the diagonal lemma. — Andrew M
Gödel's theory T is an unholy concoction of pure logic + number theory.
Take for example the sentence S1="Socrates is human". The truth status of this sentence is determined externally. In terms of the number theory in which we are operating, the truth of this sentence is just being axiomatized. It constitutes an axiomatic extension to the system. It has nothing to do with anything that would otherwise be provable from number theory.
Theory T happily supports this type of sentences. Pure logic (as opposed to number theory + logic) does not try to figure out the truth of basic sentences. This information is always axiomatically supplied from outside the system.
The sentence S2="12 > 3" is different. It is a sentence of which we can determine the provability in number theory itself. Its provability is not externally supplied.
True(S) will actually work fine. It is True(%S) that does not work. Funnelling sentences through the number-theoretical module of the system in order to determine their truth is not allowed. However, you are still allowed to funnel it through the pure logic module of the system with True(S). -
 Andrew M
1.6kTrue(S) will actually work fine. It is True(%S) that does not work. Funnelling sentences through the number-theoretical module of the system in order to determine their truth is not allowed. However, you are still allowed to funnel it through the pure logic module of the system with True(S). — alcontali
Andrew M
1.6kTrue(S) will actually work fine. It is True(%S) that does not work. Funnelling sentences through the number-theoretical module of the system in order to determine their truth is not allowed. However, you are still allowed to funnel it through the pure logic module of the system with True(S). — alcontali
OK. What I'm suggesting is that an arithmetic sentence could be defined as only being true (or false) if it is, in principle, provable from axioms (or in the case of a false sentence, that its negation is provable). On that premise, the Godel sentence:
- This sentence is not provable
would be neither true nor false. To expand:
If the Godel sentence were false then it would be provable. But in a consistent system, only true sentences are provable. Therefore it cannot be false.
Alternatively, if the Godel sentence were true then it would not be provable. But that contradicts the above premise that true sentences are provable. Therefore it cannot be true.
Thus, on the initial premise above, the Godel sentence would not express a proposition. In this way, it would parallel the Liar sentence which is also normally considered neither true nor false. And also the Halting problem, which no program can in principle satisfy. -
 alcontali
1.3kBut that contradicts the above premise that true sentences are provable. — Andrew MAlternatively, if the Godel sentence were true then it would not be provable. But that contradicts the above premise that true sentences are provable. Therefore it cannot be true. — Andrew M
alcontali
1.3kBut that contradicts the above premise that true sentences are provable. — Andrew MAlternatively, if the Godel sentence were true then it would not be provable. But that contradicts the above premise that true sentences are provable. Therefore it cannot be true. — Andrew M
There is a complicating twist to this.
A theory such as PA can have more than one model. Say that a theory has five models. A sentence could be true in one model but not in the other four models. Semantic completeness means: if a sentence is true in all models of the theory, then the sentence is also provable in the theory.
So, what does it mean that a statement S is true but not provable in theory T? It simply means that theory T has other models than the one you are considering, say, the standard model, and that in at least one of these alternative models, S is blatantly false.
Gödel's incompleteness theorems also imply the existence of non-standard models of arithmetic. The incompleteness theorems show that a particular sentence G, the Gödel sentence of Peano arithmetic, is not provable nor disprovable in Peano arithmetic. By the completeness theorem, this means that G is false in some model of Peano arithmetic.
The standard model of PA is N, the natural numbers.
You can create an example non-standard model for PA by axiomatizing the existence of a transfinite cardinal in PA in addition to N, the natural numbers. From the compactness theorem follows that this non-standard model is still a legitimate model of PA.
But that contradicts the above premise that true sentences are provable. — Andrew M
So, no, because such sentence could be true in one model of the theory and false in another. Therefore, true sentences are not necessarily provable. According to semantic completeness, provability means: true in all models of the theory (without exception).
Note:
Objects can only be defined uniquely up to unique isomorphism. So, all these models satisfying PA are isomorphic with the natural numbers, but are not necessarily the natural numbers. These carbon copies of the natural numbers each start at another transfinite cardinal, and start counting up from there.
Everything you claim from the axiomatic PA definition of natural numbers -- for such claim to be provable in PA -- must also hold to be (logically) true for each of these carbon copies of the natural numbers. Otherwise, it will only be true for the original natural numbers, but not provable from their axiomatic definition (i.e. provable from PA). -
 Andrew M
1.6kThanks for the explanations.
Andrew M
1.6kThanks for the explanations.
Gödel's incompleteness theorems also imply the existence of non-standard models of arithmetic. The incompleteness theorems show that a particular sentence G, the Gödel sentence of Peano arithmetic, is not provable nor disprovable in Peano arithmetic. By the completeness theorem, this means that G is false in some model of Peano arithmetic. [Wikipedia] — alcontali
OK. Does that just mean that non-standard models of Peano arithmetic are inconsistent? Or is there more to it than that?
The next sentence from that Wikipedia entry says:
However, G is true in the standard model of arithmetic, and therefore any model in which G is false must be a non-standard model.
Can there be an alternative arithmetic model where the Godel sentence is neither true nor false?
And, if so, can such a model be both consistent and complete? -
 alcontali
1.3kDoes that just mean that non-standard models of Peano arithmetic are inconsistent? Or is there more to it than that? — Andrew M
alcontali
1.3kDoes that just mean that non-standard models of Peano arithmetic are inconsistent? Or is there more to it than that? — Andrew M
A model cannot be inconsistent. Only a theory could be.
A model in PA is a carbon copy of the natural numbers. It is just a structure, which is a set, such as: 1,2,3, ... along with a collection of operators {+,-,*,/} that operate on that set. structure = two-tuple: (set, operators).
The standard model of PA is ({1,2,3,...},{+,-,*,/})
A theory is a collection of theorems, i.e. sentences about a model. PA is a theory. If PA is true in structure M, then M is a model of PA. If PA does not hold true in M, then it would simply not be a model of PA.
Hence, if non-standard models of PA were inconsistent with PA, they would by definition not be models of PA.
There is no such thing as the consistency of a model. They fit the bill (of the theory) or they don't.
Can there be an alternative arithmetic model where the Godel sentence is neither true nor false? — Andrew M
A theorem S will be unprovable in theory T, if S has a different truth status across T's models. I am not sure that model theory implies that this is the only possible reason for unprovability.
I am not sure about the answer. I am not sure that the existence of nonstandard models is the only source of unprovability/undecidability in PA. This is about the limitations of model theory. This is a hard question! -
 Andrew M
1.6kThere is no such thing as the consistency of a model. They fit the bill (of the theory) or they don't. — alcontali
Andrew M
1.6kThere is no such thing as the consistency of a model. They fit the bill (of the theory) or they don't. — alcontali
OK. So, per the earlier Wikipedia quote, what does it mean that the Godel sentence (G) is false in some (non-standard) model of Peano arithmetic? Since that implies that G is provable, isn't that an inconsistency?
This is a hard question! — alcontali
I see the issue as similar to the Halting problem. To the question of whether the pathological program halts or loops, the answer is that such a program cannot exist. Similarly, to the question of whether the Godel sentence is true or false, the answer, it seems to me, is that without a process for inferring truth (or falsity), such a sentence cannot be truth-apt. It's simply a pathological sentence like the Liar sentence. -
 alcontali
1.3kSo, per the earlier Wikipedia quote, what does it mean that the Godel sentence (G) is false in some (non-standard) model of Peano arithmetic? Since that implies that G is provable, isn't that an inconsistency? — Andrew M
alcontali
1.3kSo, per the earlier Wikipedia quote, what does it mean that the Godel sentence (G) is false in some (non-standard) model of Peano arithmetic? Since that implies that G is provable, isn't that an inconsistency? — Andrew M
No, ~G would still not be provable, because to that effect G needs to be false in ALL models.
Provability of G means: G is true in ALL models
Provability of ~G means: G is false in ALL models
If it is true in some and false in others, that means: it is not provable nor disprovable in the theory.
Truth is attached to a model. Provability is attached to the theory, which may have more than one model. If a theorem has mixed truth status in the models then it will not be provable or disprovable in the theory.
Example.
Theory T has model M1 and M2.
Sentence Sa is true in M1 and true in M2. Hence, Sa is provable in T.
Sentence Sb is false in M1 and false in M2. Hence, ~Sb is provable in T.
Sentence Sc is true in M1 and false in M2. Hence, Sc is not provable and ~Sc is not provable in T.
What is a theory? A set of rules.
What is a model? A set of objects (with operators on them)
At first glance, PA arithmetic theory, which is a set of rules, describes just the natural numbers. However, that turns out not to be true. There are other sets of numbers that also satisfy the rules of PA. Hence, the natural numbers are considered the "standard" model, while these alternatives that also satisfy these rules, are considered "non-standard" models.
Imagine that you try to describe a car by giving rules which objects must satisfy in order to be considered a car. It must have wheels. It must have a steering wheel. And so on. At this point, the set of Ford vehicles (model 1) satisfy the rules, but also the set of Harley-Davidson motorbikes (model 2).
No matter how precisely you design the rules of PA arithmetic, there will always be other models than the natural numbers that will satisfy these rules. The set of objects described will be unique only up to an isomorphism. Any theory that is complex enough will exhibit the same problem of having multiple models. If a theorem is true in some models but false in other ones, then this theorem will not be provable in the theory. That is the basic idea of model theory. -
 Andrew M
1.6kSo, per the earlier Wikipedia quote, what does it mean that the Godel sentence (G) is false in some (non-standard) model of Peano arithmetic? Since that implies that G is provable, isn't that an inconsistency?
Andrew M
1.6kSo, per the earlier Wikipedia quote, what does it mean that the Godel sentence (G) is false in some (non-standard) model of Peano arithmetic? Since that implies that G is provable, isn't that an inconsistency?
— Andrew M
No, ~G would still not be provable, because to that effect G needs to be false in ALL models.
Provability of G means: G is true in ALL models
Provability of ~G means: G is false in ALL models
If it is true in some and false in others, that means: it is not provable nor disprovable in the theory. — alcontali
Working through the logic, G is:
- This sentence is not provable
So ~G is:
- The sentence "This sentence is not provable" is not true
Now ~G (as with G) is not provable since it can't be derived from the axioms of the theory. Therefore, according to what you've said, ~G (as with G) must be true in some models of the theory and false in others.
However since ~G negates its inner sentence, ~G unpacks further as:
- The sentence "This sentence is not provable" is provable
Or, more simply:
- G is provable
If that is correct, then it seems that ~G can't be true in any model of the theory, since G isn't provable. -
 alcontali
1.3kIs that the same as saying, "If, in a nonstandard model, G is false, then G is provable there"? — Andrew M
alcontali
1.3kIs that the same as saying, "If, in a nonstandard model, G is false, then G is provable there"? — Andrew M
No, provability means: true (or false) in ALL models. The lack of provability in theory T is caused by the existence of a mixture of true and false in its models. True in some models and false in others. -
 Andrew M
1.6kYes, I get that provability means true (or false) in all models.
Andrew M
1.6kYes, I get that provability means true (or false) in all models.
What I don't get is why the negation of G shouldn't be interpreted as saying that G is provable. Since G is saying that G is not provable, then it seems to me that to negate G is just to say that G is provable.
We're obviously interpreting ~G differently, but I don't understand how you're interpreting it, nor what you think I'm specifically getting wrong in the above. -
 alcontali
1.3kWhat I don't get is why the negation of G shouldn't be interpreted as saying that G is provable. Since G is saying that G is not provable, then it seems to me that to negate G is just to say that G is provable.
alcontali
1.3kWhat I don't get is why the negation of G shouldn't be interpreted as saying that G is provable. Since G is saying that G is not provable, then it seems to me that to negate G is just to say that G is provable.
We're obviously interpreting ~G differently, but I don't understand how you're interpreting it, nor what you think I'm specifically getting wrong in the above. — Andrew M
Yes, there is a problem there. In a nonstandard model it would say that G is provable, while it isn't. Wikipedia says the following about that problem:
Arithmetic unsoundness for models with ~G true
Assuming that arithmetic is consistent, arithmetic with ~G is also consistent. However, since ~G means that arithmetic is inconsistent, the result will not be ω-consistent (because ~G is false and this violates ω-consistency).
ω-consistency is inconsistency at the level of a combination of universally quantified propositions:
It is different from outright inconsistency:
Having models with ~G true causes trouble, but does not end up rendering arithmetic inconsistent, only ω-inconsistent.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum











