-
 Gregory
5kTo apply infinity to matter in the universe seems unavoidable. Irrational numbers too go on forever. So Aristotle is wrong. Non-organic things can only be defined by cohesion. A lamp may be one thing for us but another for another culture. If the lamp shade is not sufficiently "stuck" to the lamp, you have two objects. So nominalism is justified from every angle, contra Aristotle. Now, finite geometry has been a complete failure. Indeed, I don't know much math. But I don't feel like those who do truly empathize with the problem of something being spatially infinite and finite in the same respect. I'm fine with a round triangle, as long as others see my point that this is where math leads
Gregory
5kTo apply infinity to matter in the universe seems unavoidable. Irrational numbers too go on forever. So Aristotle is wrong. Non-organic things can only be defined by cohesion. A lamp may be one thing for us but another for another culture. If the lamp shade is not sufficiently "stuck" to the lamp, you have two objects. So nominalism is justified from every angle, contra Aristotle. Now, finite geometry has been a complete failure. Indeed, I don't know much math. But I don't feel like those who do truly empathize with the problem of something being spatially infinite and finite in the same respect. I'm fine with a round triangle, as long as others see my point that this is where math leads -
 Metaphysician Undercover
14.7kWhat would it be made of? — tim wood
Metaphysician Undercover
14.7kWhat would it be made of? — tim wood
It's just a line. It signifies a spatial dimension. Why does it have to be "made of" something? You may as well be asking me what a dimension is made of. It's an idea.
Is it reasonable (however defined) for philosophers who have not studied mathematics to argue basic principles of the subject? — John Gill
It may be the case, that a person was discouraged from entering the field of mathematics because its fundamental principles appeared to be very difficult to understand. So this future-to-be philosopher could not understand mathematics and went on to become a philosopher instead. Then the philosopher goes back to revisit the fundamental math principles and finds that they appear to be totally irrational and this is why they cannot be understood. In this case it is reasonable for a philosopher who has not studied mathematics to ask the mathematicians to justify their basic principles.
Though you cannot measure how long a point is (since it has no length, as per definition) you can identify a point. And we do so through a complex process that involves the movement of our bodies (if we're talking about identifying points in physical space, that is.) — Magnus Anderson
Points don't exist in physical space. According to the description they are non-spatial. So I don't see how you can identify something which has absolutely no spatial extension by moving your body. Care to explain how you think you might do that?
There are many things that have no size but that nonetheless exist (and are not logically contradictory, illogical or otherwise irrational.) The word "existence" does not imply size. For example, colors and feelings exist, and yet, they have no size. A typical counter-argument is that colors are light waves and that light waves have size (their wavelength.) But light waves are not colors. Rather, light waves are things that cause colors. (This is evident in the fact that light waves can exist without conscious beings whereas colors can't.) — Magnus Anderson
I agree that there are many things we can talk about, which do not have spatial existence (God being one of them). The problem is with the claim that a line, which is supposed to have spatial existence, is made up of non-spatial things. -
 Gregory
5k"The world is unlike unto itself.. the one is the sphere of appearance... We have to think pure flux, opposition within opposition itself, or Contradiction. For in the distinction, which is an internal distinction, the opposite is not only one of two factors- if it were so, it would not be an opposite, but a bare existent- it is the opposite of an opposite, or the other is itself directly and immediately present within it.... it is that world itself and its opposite in single unity. Only thus is it distinction as internal distinction; in other words, only then is it in the form of Infinity." Hegel, Phenomenology of Mind
Gregory
5k"The world is unlike unto itself.. the one is the sphere of appearance... We have to think pure flux, opposition within opposition itself, or Contradiction. For in the distinction, which is an internal distinction, the opposite is not only one of two factors- if it were so, it would not be an opposite, but a bare existent- it is the opposite of an opposite, or the other is itself directly and immediately present within it.... it is that world itself and its opposite in single unity. Only thus is it distinction as internal distinction; in other words, only then is it in the form of Infinity." Hegel, Phenomenology of Mind -
 Metaphysician Undercover
14.7k(Imo) egg-zackly! That is, everything in and of math is an idea. Being ideas, they're subject to definitions, not reality in any sense at all. You wanna talk my ideas, then you have to know my definitions, and vice versa. As such, there is no "how it is." But there is, however, "how I say it is." — tim wood
Metaphysician Undercover
14.7k(Imo) egg-zackly! That is, everything in and of math is an idea. Being ideas, they're subject to definitions, not reality in any sense at all. You wanna talk my ideas, then you have to know my definitions, and vice versa. As such, there is no "how it is." But there is, however, "how I say it is." — tim wood
Right, now the problem is the inconsistency between the definition of a point, and the definition of a line. A "point" is completely dimensionless. A "line" has dimension, yet the "line" was said to be "made up" of points. Do you see the inconsistency? No matter how many dimensionless things you add together you will not produce a thing with dimension.
But maths are useful in the world. As a consequence, it is necessary - and certainly useful - to not confuse the theoretical/idea side with the practical/reality side. There are "points" and there are "lines" and what either means, or any of a lot of other terms found in both theoretical and practical applications mean, is simply a matter of the application and the relevant understandings, without which nonsense reigns. — tim wood
So what are you saying? We ought to just get rid of definitions altogether, and mathematicians will use these terms however they please? Then we can produce some sort of idea of what each mathematician means by looking at each one's use of the terms. That sounds very difficult, because there would be nothing to encourage consistency of use.
...then they'd be making excellent arguments - excepting that with the qualification they might be trivial and not worth making. — tim wood
What is trivial to one person is important to another. So for instance, I think that it is very significant that a "point" is incompatible with a "line", and that the ratio between the circumference and diameter of a circle is irrational, and that the relation between two perpendicular sides of a square is irrational. You, as well as many others, might think that these matters are "trivial" and uninteresting.
But then why do you partake in threads like this? I've seen the same tactic from atheists who say that whether or not God exists is really unimportant, yet they will argue incessantly that god does not exist. So, what is really important to them is whether or not a person believes that God exists. But how could this be important if whether or not God exists is unimportant?
Now, I'll ask you how is it possible that the "true" nature of the "point", and the "line", and the fact that there is inconsistency between these conceptions, is trivial, when the mathematician will claim that consistency is of the utmost importance? -
 Magnus Anderson
355Points don't exist in physical space. According to the description they are non-spatial. — Metaphysician Undercover
Magnus Anderson
355Points don't exist in physical space. According to the description they are non-spatial. — Metaphysician Undercover
I am not sure why you think so, Points do exist (both in time and space.) Consider that at any point in time, you occupy certain point in space. So there exist at least some of the points that we can imagine. Points that do not exist cannot be occupied by anything under any set of circumstances.
Physical space is made out of points. The fact that physical space is made out of things that have no size (points) does not mean that it has no size itself. Not sure why you think so. -
 Gregory
5kNumbers apply to the world. One microphone is not two. Points show that objects in the world are both infinite and finite. Escher paintings exist but what we are talking about is matter, not perception. The eternal halving of the hypotenuse shows there is no final term. The.Pythagorean theorem, when we say the smallest units are the right sides, leads to length being irrational in the hypotenuse. Contradictions everywhere
Gregory
5kNumbers apply to the world. One microphone is not two. Points show that objects in the world are both infinite and finite. Escher paintings exist but what we are talking about is matter, not perception. The eternal halving of the hypotenuse shows there is no final term. The.Pythagorean theorem, when we say the smallest units are the right sides, leads to length being irrational in the hypotenuse. Contradictions everywhere -
 Gregory
5kIrrational numbers are not only irrational, but they go on forever while spatially being finite. The same applies to pi and the circumference in the sense of infinite fintude. Maybe math proves that something can come from nothing since spatially finite comes directly with spatial infinity. Nothingness is not dark, but white and shining says the Tibetan Book of the dead
Gregory
5kIrrational numbers are not only irrational, but they go on forever while spatially being finite. The same applies to pi and the circumference in the sense of infinite fintude. Maybe math proves that something can come from nothing since spatially finite comes directly with spatial infinity. Nothingness is not dark, but white and shining says the Tibetan Book of the dead -
 fishfry
3.4kIrrational numbers are not only irrational, but they go on forever ... — Gregory
fishfry
3.4kIrrational numbers are not only irrational, but they go on forever ... — Gregory
No, this is not true. But it's such a common misunderstanding that a bit of exposition is in order.
One of the first things to know about the philosophy of math is the distinction between a number, on the one hand, and a representation of a number, on the other. 5, five, fünf, cinco, 2 + 2 + 1, 4.999..., the number of points on a mystical pentagram, and "half of ten" are all distinct representations of the same number.
So what's a number? If one is a Platonist, the number 5 is the abstract thingie out in the Platonic world "pointed to" or represented by each of those representations that I listed. If one rejects Platonism, I suppose we could get by saying that the number 5 is the collection of all possible finite-length strings of symbols that represent that number. (Although when it comes to numbers, an anti-Platonist has a tough row to hoe, suggesting that a Martian mathematician would not necessarily know the concept of five, or that there weren't five things before there were people to count them).
But whether one is a Platonist or not, one must distinguish between the abstract concept of the number 5 and any of its many representations.
Now, a real number is a real number. The exact definition of a real number is a technical matter for math majors and isn't too important at the moment. What is important is to understand that a real number HAS a decimal representation, sometimes two! But it is wrong to say that a real number IS a decimal representation.
One can be forgiven for wrongly believing the latter, since it's what we tell high school students. And even in technical disciplines, the distinction's not important. A working professional engineer, even a working professional research physicist, does not need to know or care about the distinction between a real number and its decimal representation.
There are only two classes of people who need to carefully make this distinction: mathematicians, who are trained on this topic in their undergrad years; and philosophers, who SHOULD BE but often aren't cognizant of the distinction.
Now decimal notation happens to be broken. Some perfectly sensible and familiar rational numbers, such as 1/3 = .3333333..., have infinitely-long decimal representations. That's not because 1/3 is broken; it's because decimal representation is.
Likewise some perfectly familiar integers, like 5 = 4.9999..., have TWO distinct decimal representations. Again, this isn't because real numbers are broken [though for the record, in this post I'm not necessarily arguing that they're not!]; it's because decimal representation has these well-known flaws.
The same applies to pi and the circumference in the sense of infinite fintude. — Gregory
So what about a real number like ? Does represent or encode an infinite amount of information? NO it does not! I will now show three distinct finite length descriptions of that uniquely characterize that particular real number:
* The first is the famous Leibniz series for :
This is a finite string of symbols in a formal language that unambiguously characterizes the real number , and that, Platonism or not, would without doubt be recognized as such by a Martian mathematician.
* But ok suppose that you don't like those dots. We can compactify the notation as follows:
[NOTE: Typo in formula corrected].
* But ok, perhaps you don't like the notion of infinitary processes, even in compact notation that only uses finitely many symbols in a formal language. In this case:
is the smallest positive zero of the sine function.
Our Martian mathematician would have no trouble agreeing with that. And it's a finite string of symbols written in plain English, with no infinitary process in sight, that uniquely and unambiguously characterizes the real number .
So in fact the real number encodes only a finite amount of information. This is true also of every real number you can name, such as the square root of 2, the base of the natural logarithm , the golden ratio , and so forth.
Are there real numbers that can't possibly be expressed with a finite amount of information? Most definitely. These are the noncomputable real numbers as defined by Alan Turing in his landmark 1936 paper that defined the nature of computation. In constructive math, one doubts the existence of such numbers; but that discussion is for another time.
Takeaway: Every real number that you know encodes only a finite amount of information and can be expressed using only a finite number of symbols. Decimal representation is defective to the extent that some reals require infinitely many symbols and others have two distinct representations. But a real number is not any of its particular representations, so this is not a philosophical problem.
Maybe math proves that something can come from nothing since spatially finite comes directly with spatial infinity. — Gregory
Math proves no such thing, since your examples don't hold up to mathematical scrutiny. But more strongly, as many posters have already noted (hundreds if not thousands of times on this site over the years), math can prove nothing at all about the world. At best, math is a super-handy (and as Putnam and Quine might put it, indispensable) tool for building mathematical models of physical theories. Newton and Einstein both used math to express their respective theories of gravity; even though neither, strictly speaking, is true. They're both just approximations that describe the experiments and observations we're able to do with our current level of technology. I hope this point is clear not only here, but once and for all on this forum. Science isn't true. Science is our best mathematical model that fits the observations we're able to make with the equipment we're able to build subject to technology and funding. (As the government bureaucrat pointed out in the film, The Right Stuff: "No bucks, no Buck Rogers!")
Nothingness is not dark, but white and shining says the Tibetan Book of the dead — Gregory
Way cool, but perhaps a little off the mark in this particular conversation. -
 Metaphysician Undercover
14.7kA point in geometry is a location. It has no size i.e. no width, no length and no depth. — tim wood
Metaphysician Undercover
14.7kA point in geometry is a location. It has no size i.e. no width, no length and no depth. — tim wood
Think about what you're saying tim, "a location" without any size is nonsensical. What could possibly identify that location unless there was something there with size? If there is a dot, to show the location, there is something there with size. If there is no dot, then there is no identified location. But "location" implies particularity and particularity is identifiable. How can the mentioned "location" be a location without something to show that location.? Otherwise it is just imaginary. And an imaginary location is not a real location, therefore not a location at all. It seems very clear that it is contradictory to say that a point has no size and it is also a location.
Well here's an example of confusion in your thinking. We agree that points and lines are ideas, therefore the proper objects of definitions. The which having nothing to do with true. But you mention consistency of definitions. What definitions? Your definitions? But you want to "add" points. How, exactly, do you add points? — tim wood
It's no wonder I appear confused, you totally misuse words. There is no such thing as "objects of definitions", unless you are using "object" in the sense of "goal". And you are clearly not talking about the goals of definitions. These are subjects, not objects. Points, lines and other defined principles, ideas, are subjects. We are taught the subjects of knowledge, not the objects of knowledge. If you call them "objects" you imply the existence of some unjustified Platonic realm full of non-spatial objects.
So if you want me to agree with you on any definition of "point", we'd have to start with a principle to avoid such a category mistakes. We cannot say that a point is a location because locations are marked by objects with spatial extension, not subjects. Therefore we must disambiguate. Is a point a non-spatial idea (subject of knowledge), or is it a particular spatial location (object)? We can't have both without contradiction.
am not sure why you think so, Points do exist (both in time and space.) Consider that at any point in time, you occupy certain point in space. So there exist at least some of the points that we can imagine. Points that do not exist cannot be occupied by anything under any set of circumstances. — Magnus Anderson
You said points have no size. I do not see how any part of time could have no size. If it has no size, then no time is passing at that "point", therefore it is not part of time. The same principle holds for space. If it has no size, then it cannot be part of spatial existence, because there is no space there. It is very clear to me, that if points have no size, then they are excluded from space and time, because things existing in space and time have size. Having size is what makes them spatial-temporal. Do you not understand this? -
 SophistiCat
2.4kQuestion: on a ruler one can mark units, then divide the units in half, thirds ( I think), quarters, & etc. But there is no way to mark an exact irrational length on the ruler - unless a line representing an irrational distance is constructed (like the square root of two) and marked on the ruler by direct measurement. Correct? — tim wood
SophistiCat
2.4kQuestion: on a ruler one can mark units, then divide the units in half, thirds ( I think), quarters, & etc. But there is no way to mark an exact irrational length on the ruler - unless a line representing an irrational distance is constructed (like the square root of two) and marked on the ruler by direct measurement. Correct? — tim wood
Depends on what you mean by marking off distance on a ruler. If you mean real rulers and real markings, then it's kind of hard to even talk about exact distances. If you have an idealized model in mind - putting a point somewhere on a segment of a straight line, then why can't we mark off an irrational distance? If you make a mark somewhere at random, the distance it marks off is pretty much guaranteed to be an irrational number. -
 jgill
4kIn math a point is usually a position dependent upon a framework. Take away the framework, does the point still exist? It seems to since it crops up in framework after framework. Is a point then eternal? Is it possible to destroy a point, or would that require a point being material? :roll:
jgill
4kIn math a point is usually a position dependent upon a framework. Take away the framework, does the point still exist? It seems to since it crops up in framework after framework. Is a point then eternal? Is it possible to destroy a point, or would that require a point being material? :roll: -
 Gregory
5kMathematical equations don't really deal with this problem. This has to do with matter. Split a banana in two and the two halves equal the whole banana. The process of division goes on to infinity, so the banana is infinite and finite at the same time. That's Zeno (when not applied to motion, which has the same problem). Many is always many when it comes to size/volume. So the world is an Escher painting in the flesh. I don't see why Zeno's paradox is not a paradox but Banach-Tarski is. The latter flows directly from the former, and there is no BT without Zeno
Gregory
5kMathematical equations don't really deal with this problem. This has to do with matter. Split a banana in two and the two halves equal the whole banana. The process of division goes on to infinity, so the banana is infinite and finite at the same time. That's Zeno (when not applied to motion, which has the same problem). Many is always many when it comes to size/volume. So the world is an Escher painting in the flesh. I don't see why Zeno's paradox is not a paradox but Banach-Tarski is. The latter flows directly from the former, and there is no BT without Zeno -
 jgill
4kI don't see why Zeno's paradox is not a paradox but Banach-Tarski is. The latter flows directly from the former, and there is no BT without Zeno — Gregory
jgill
4kI don't see why Zeno's paradox is not a paradox but Banach-Tarski is. The latter flows directly from the former, and there is no BT without Zeno — Gregory
I don't know about that, never having gone through the proof of B-T. However . . .
Wiki: Unlike most theorems in geometry, the proof of this result depends in a critical way on the choice of axioms for set theory. It can be proven using the axiom of choice, which allows for the construction of non-measurable sets, i.e., collections of points that do not have a volume in the ordinary sense, and whose construction requires an uncountable number of choices. -
 Metaphysician Undercover
14.7kSo mock me as you like, but you're actually mocking the rest of the world.. — tim wood
Metaphysician Undercover
14.7kSo mock me as you like, but you're actually mocking the rest of the world.. — tim wood
Sure, I'm fine with this, but it's more a case of pointing out a very common and simple mistake, rather than a case of "mocking".
Are you prepared to argue that an idea has a size? — tim wood
No, I'm not prepared to argue that an idea has a size, but as I've demonstrated, I'm prepared to argue that a location has a size. Therefore, if a point is an idea, and has no size, it is impossible that a point is a location.
Now, it seems you cannot keep track of the distinction between theoretical math and the math of the world. In the world, most locations have size, for lots of reasons that have almost zero to do with size. — tim wood
What's this supposed to mean, locations have size for reasons unrelated to size? Let me remind you of my argument. All locations have size. That's why a point cannot be a location.
Maybe I should pay more attention to what you've written here. — tim wood
I think so. You seem to think that I was arguing that a point must have size. That's not the case, I was arguing that a location has size, but a point does not. I thought I made it clear that what I was arguing is that if a point has no size it is not a location.
There is no issue between us. — tim wood
There clearly is an issue. You said that a point has no size, and that a point is a location. As I pointed out, the two are contradictory. So which do you think is the case? Does a point have no size, or is a point a location? Since the two definitions are contradictory we cannot proceed until we resolve this matter.
To suggest that a point has no size in theory, yet has size in practise is an unacceptable solution, because this would mean that the definitions of the theory contradict the definitions of practise, leaving the theory with all its definitions absolutely useless. To have a useful theory requires consistency between the definitions of the theory, and the definitions employed in application. That's what an acceptable theory is, one which is actually applicable in practise.
Maybe you could cut and paste your definition here. And resolve the difficulty of uncountable infinities of infinite size created when points have any size at all. — tim wood
I am not proposing any definitions. I am just arguing that the ones proposed here are not good, due to their contradictions involved with how they relate a point to a line..
So, I am happy to start with the assumption that a point has no size, and is immaterial, as an idea, like you suggest. Now the question is how does a point relate to a line. If we can agree that a line also has no size, and is immaterial, as an idea, then we might be on our way to making some progress toward describing the relationship between a point and a line. Let's consider a problem together then. Some people might say that two points, and a line between the two points creates something measurable. I don't think so. I think that this is just an idea, an idea which exists as a tool for measuring. So the line segment spoken of here is actually not something which could be measured. -
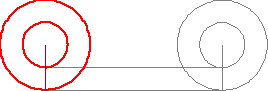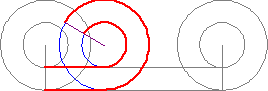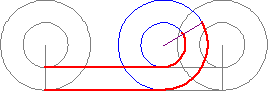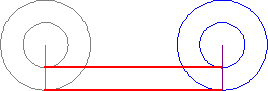
 jorndoe
4.2k, just in case you're new around here, these things come up every now and then — Zeno "impossible!" ∞ "paradox" 1/0 ... — usually due to some misunderstandings. :)
jorndoe
4.2k, just in case you're new around here, these things come up every now and then — Zeno "impossible!" ∞ "paradox" 1/0 ... — usually due to some misunderstandings. :) -
 Metaphysician Undercover
14.7kYou're just being ridiculous. — tim wood
Metaphysician Undercover
14.7kYou're just being ridiculous. — tim wood
What's ridiculous is that people like you refuse to accept the obvious, and keep touting your contradictory definitions.
Thanks jorndoe, I've never seen that circle paradox before. If you look, you'll see that the centre of the circle moves just as far relative to the horizontal surface as the point on the circumference does, and it's not rolling at all. So the rolling wheel creates a movement which is other than just the circumference moving around the centre, it "carries" the centre along in a horizontal motion relative to the ground. That's why the wheel's a good mode of transport, you put an axle in the centre and you can "carry" stuff. So we have carriages and cars.
In the depiction therefore, all horizontal movement is carriage. No point in the wheel, accept the centre, actually makes that horizontal line, so the line represents only the movement of the centre. The movement of any point in the wheel would make an arc, not a horizontal line. Therefore the horizontal line only represent carriage. The point part way between the circumference and the centre, is not rolling along the ground, it is being carried, And since it is not in the centre it would be carried in an arc; a bumpy ride..
Now, take the point on the circumference and follow the arc that it makes. Is that arc the same length as the horizontal line? No, obviously it's much longer. Why is it so much longer? It's longer because that point on the wheel, like any other point, is being carried, along with also moving in that circular motion. So the distance it actually traverses is much longer than the horizontal line. The horizontal line on the ground represents the length of the circumference, but it doesn't represent the movement of any part of the wheel. It is a fictional line of movement which represents the movement of the centre, but transposed to a parallel, on the ground. And the other line is also such a transposed parallel, not representing the movement of any point on the wheel. .
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum