-
creativesoul
12.2k
Actually I had overlooked and/or neglected cases where something is exactly 15 billion years of age, but I think I've understood the logical notation you're advocating here. That example didn't quite fit, but could have had I not employed "younger" and instead said something like "everything in the universe is not older than 15 billion years", or "there is not something in the universe that is older than 15 billion years". Both of these are semantically equivalent to "nothing in the universe is older than 15 billion years".
When everything is X, then nothing is not X. When everything is not X, then nothing is X.
In both cases, the term "nothing" is semantically equivalent to "everything". This happens as a result of shared common referents(both terms pick out the same things), regardless of what's being said about them(aside from contradiction). So far, all of this seems fine by me.
My issue involves...
...(if there are zero things to be had and you have all zero of them), — Pfhorrest
Saying "you have all zero of them" neglects the fact that in order to have all of anything requires that there first be something to have. Having all of something requires at least one thing. Zero things is not at least one thing. Zero things is nothing, and not in the same sense as when the term "nothing" is used as a means to pick out everything. -
 Pfhorrest
4.6kThis just goes back to how having all of something just means there are none you don’t have. If there are zero things, and you have zero of them, then there are no things (out of those zero things in question) that you don’t have. You have zero out of zero, which is the most out of zero you could possibly have, i.e. all of it.
Pfhorrest
4.6kThis just goes back to how having all of something just means there are none you don’t have. If there are zero things, and you have zero of them, then there are no things (out of those zero things in question) that you don’t have. You have zero out of zero, which is the most out of zero you could possibly have, i.e. all of it.
It’s weird, yeah, but that’s because we don’t usually talk about empty sets, because there’s almost no practical need to. -
god must be atheist
5.1kPfhorrest, at some stage one has to suppose that the unwillingness to learn displayed here is wilful. When one reads:
Years of indoctrination in the wrong logic hasn't touched me. I hope it never will.
— god must be atheist
the only sensible thing to do is to walk away. — Banno
Banno, the preceding page that has posts since the post of the above quote shows that I am not stupid, or unwilling to learn. It ought to show you the error of your way of reasoning. It is not my "unwillingness to learn" that is the stupid thing around here; the "stupid" was the ill logic that PfHorrest was trying to teach me. You, PfHorrest and CreativeSoul have argued a page worth preceding this post of mine, without resolution. Because, basically, if you stick to your wrong guns, and you are emotionally committed to stick by them, then you can't be convinced of your wrongness in logical terms. And I put it to you, Banno and PfHorrest, that you two are committed emotionally to the wrong argument.
What happened here? This:
PfHorrest showed me a Venn diagram that was self-contradictory or nonsensical. When I told him that, he said, "forget the Venn diagram".
Then later CreativeSoul pointed out to you and to PfHorrest that to have everything red in a box, you must have at least on thing in the box, because nothing (in case of an empty box) can't be red. You two, PfHorrest and Banno, tried to deny this with logical arithmetics, which was a futile and -- between us -- unthinking move.
This is where the impasse occurred, and I saw this happening, yet you, Banno, and PfHorrest, THOUGHT OF ME IN A VOCALIZED (WRITTEN) WAY AS THE STUPID ONE WHO IS UNWILLING TO LEARN, whereas what happened was that I saw the error of your ways, which you two are still unwilling to see or to admit to.
I pulled out of this futile thread, because you are unwilling to admit to obvious facts, and I was actually hurt and dismayed and filled with bitterness when YOU TWO, BANNO and PFHORREST called me stupid (not verbatim, but in so many other words). -
god must be atheist
5.1kIt’s weird, yeah, but that’s because we don’t usually talk about empty sets, because there’s almost no practical need to. — Pfhorrest
... strike "becasue there's almost no practical need to" and replace it with "because it blows our theorem to pieces making minced meat out of it." -
 Pfhorrest
4.6kPfHorrest showed me a Venn diagram that was self-contradictory or nonsensical. When I told him that, he said, "forget the Venn diagram". — god must be atheist
Pfhorrest
4.6kPfHorrest showed me a Venn diagram that was self-contradictory or nonsensical. When I told him that, he said, "forget the Venn diagram". — god must be atheist
I did explain briefly why it was not self-contradictory before moving on to a different approach, but since you're so hung up on it I can explain in more detail here.
To recap, the left circle is cases where you have "something" and the right circle is cases where you have "not everything". In other words, the left circle is cases where there are things that you have, and the right circle is cases where there are things that you don't have.
In the left crescent are cases where you have something but not not everything, or in other words both something and everything: there are some things you have, and no things you don't have, so you have all of the things there are to be had, and there are some to be had. This is the ordinary use case for "everything", but there is another we'll get to later.
In the middle intersection are cases where you have something but not everything: there are some things you have, and some things you don't have. These are the cases that you want to restrict "something" to, but in normal language and formal logic both Aristotelian and modern, "something" also applies to the left crescent: you can have something and everything, or something and not everything. I like to call this case "merely something", where the "mere" conveys the not-everything part of it.
In the right crescent are cases where you don't have something, and you do have not-everything: there are no things that you have, and there are things that you don't have. This is the ordinary use case for "nothing".
But in the outer area are the weird cases, or rather, the one single weird case: where you don't have something, and you don't have not-everything, or in other words, when you have nothing and everything: because there are no things that you have, and no things that you don't have, because there are no things at all, because the only case that falls out here is the case of an empty set.
I drew a picture:
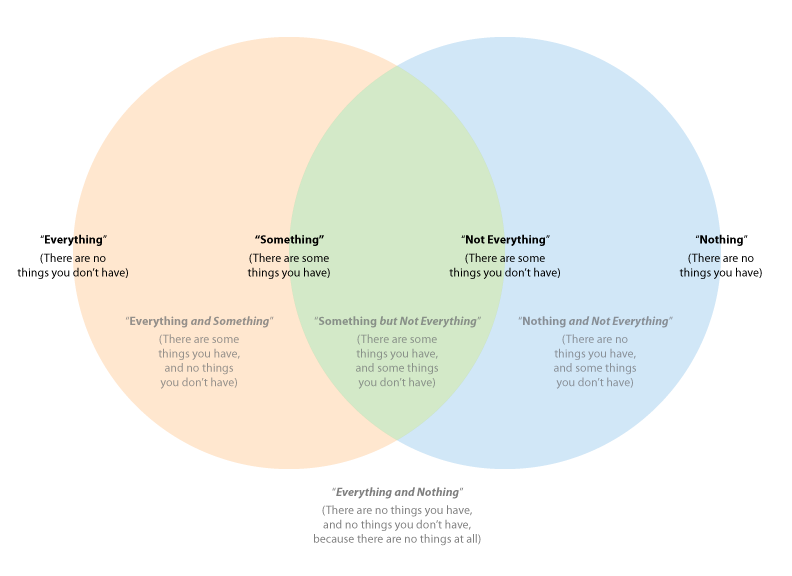
-
god must be atheist
5.1kOkay, I got something out of it.
If everything is red in the box, and everything is non-red in the box, that is reductio ad absurdum as long as something is in the box. But reductio ad absurdum also means that no such thing is possible. And lo and behold: the box is empty, therefore "everything is red" and "everything is non-red" is satisfied with no object, therefore with nothing, so there.
I eventually had to do something to try to agree with you, PfHorrest and Banno. But your reasoning did not penetrate my capacity for logic.
This reductio ad absurdum, however, proves the same thing, so I believe you now, although the steps you took to arrive at what you were trying to say are still beyond me. -
creativesoul
12.2kMy issue involves...
...(if there are zero things to be had and you have all zero of them),
— Pfhorrest
Saying "you have all zero of them" neglects the fact that in order to have all of anything requires that there first be something to have. Having all of something requires at least one thing. Zero things is not at least one thing. Zero things is nothing, and not in the same sense as when the term "nothing" is used as a means to pick out everything. — creativesoul
This just goes back to how having all of something just means there are none you don’t have. If there are zero things, and you have zero of them, then there are no things (out of those zero things in question) that you don’t have. You have zero out of zero, which is the most out of zero you could possibly have, i.e. all of it. — Pfhorrest
You're still neglecting the facts here.
In order to have all of anything, there must be something to have. Something is not equivalent to nothing. Nothing is not all of something. Nothing is not all of anything.
You say:
You have zero out of zero, which is the most out of zero you could possibly have, i.e. all of it.
"All of it"???
"The most out of zero"???
:brow:
All of IT is all of something, because "it" always refers to something. Something is not equivalent to nothing. Yet, that is precisely how you've been employing the term "nothing". I said much earlier that it looked like an equivocation fallacy to me. Now, it's certain.
It’s weird, yeah, but that’s because we don’t usually talk about empty sets, because there’s almost no practical need to.
It's not just weird. It's incoherent at best, and utter nonsense at worst. Either way, it's an equivocation of the terms "zero" and "nothing". That much is certain.
All meaningful use of "the most" presupposes "the least". "The most" makes no sense whatsoever unless there is also "the least". These two notions are both existentially and semantically dependent upon one another.
This is just plain old common sense.
"The most" and "the least" are always in direct inverse proportion to one another when dividing a whole into two unequal portions. That comparison gains complexity when dividing something into more than two unequal proportions, but the meaning of both "the most" and "the least" are still - and always are - established by comparison between a plurality of shares/portions/etc.
We talk about "the most" and "the least" after, and only after, we have something being dividing into a plurality of unequal (pro)portions. Otherwise, both notions are rendered utterly meaningless. There is no possible referent for either, unless there are referents for both.
And yet...
You've talked of "the most" of both nothing and zero, as if there is a meaningful quantitative difference to be drawn between the most of nothing and the least of nothing; as if there is a meaningful quantitative difference to be drawn between the most of zero and the least of zero.
There is not, and such talk is nonsense.
The most of zero is exactly the same as the least of zero. The most of nothing is exactly the same as the least of nothing. There is no distinction to be drawn here between the most of nothing(zero) and the least of nothing(zero) because they both have precisely the same numerical and/or quantitative value. -
 Pfhorrest
4.6kYou've talked of "the most" of both nothing and zero, as if there is a meaningful quantitative difference to be drawn between the most of nothing and the least of nothing; as if there is a meaningful quantitative difference to be drawn between the most of zero and the least of zero.
Pfhorrest
4.6kYou've talked of "the most" of both nothing and zero, as if there is a meaningful quantitative difference to be drawn between the most of nothing and the least of nothing; as if there is a meaningful quantitative difference to be drawn between the most of zero and the least of zero.
The most of zero is exactly the same as the least of zero. The most of nothing is exactly the same as the least of nothing. There is no distinction to be drawn here between the most of nothing(zero) and the least of nothing(zero) because they both have precisely the same numerical and/or quantitative value. — creativesoul
That's exactly the point. Out of a set of nothing, of zero things, there is no difference between the most of it and the least of it. But only in the case of a set of nothing, of zero things, an empty set. It is precisely because there is no difference between the most things from that set and the least things from that set that that all of it, everything from it, is the same as none of it, nothing from it. Any percent of zero is the same thing: zero. 100% of 0 = 0% of 0. In general, 100% of x ≠ 0% of x, except when x = 0. That is the only case when all of x is none of x, when x is an empty set. -
 Mapping the Medium
366“Mad Hatter: Would you like a little more tea?
Mapping the Medium
366“Mad Hatter: Would you like a little more tea?
Alice: Well, I haven't had any yet, so I can't very well take more."
How can there be anything without 'Firstness'?
How can 'nothing' be a concept at all, unless you start from the perspective of 'something'?
Top down versus bottom up thinking?
We are limited because from the perspective of self we can only know what is now, the top place to start when thinking from top to bottom. We have no concept of what the bottom may be. What we can only comprehend is that there is always something.
'Nothing' is the complete absence of Firstness. Capturing the in-between of nothingness to somethingness (the birthing of being, an idea, etc) is not an opposite or contrary, it is an emergence of continuity, perhaps from outside in to inside out. Two sides of a spinning coin. Nothingness is the exact image of the edge of the coin, when it is neither heads nor tails.
Just my thoughts. -
creativesoul
12.2kThat's exactly the point. Out of a set of nothing, of zero things, there is no difference between the most of it and the least of it. — Pfhorrest
Which renders both notions meaningless. In addition, as I've already mentioned, there's an equivocation of both terms "zero" and "nothing" as a result of using them to mean different things. -
 Pfhorrest
4.6kIt maybe renders them useless in that particular case, but we don't usually talk about that particular case for exactly that reason: nobody cares to know how many of zero things anyone has. But if "everything" is taken to mean "there aren't any you don't have" and "nothing" is taken to mean "there aren't any you have", that accurately covers all the cases anybody does actually want to talk about, and it doesn't matter that it has this weird-seeming consequence in one case that nobody cares about anyway.
Pfhorrest
4.6kIt maybe renders them useless in that particular case, but we don't usually talk about that particular case for exactly that reason: nobody cares to know how many of zero things anyone has. But if "everything" is taken to mean "there aren't any you don't have" and "nothing" is taken to mean "there aren't any you have", that accurately covers all the cases anybody does actually want to talk about, and it doesn't matter that it has this weird-seeming consequence in one case that nobody cares about anyway.
You'll have to explain this supposed equivocation between "zero" and "nothing", because I'm not seeing what you're talking about. If it helps, I'm not saying that the number zero is itself nothing; I'm saying that zero is the number of things in a set that has no things in it. -
creativesoul
12.2kIf you do not care about the logical consequences of incoherency/meaninglessness that inevitably follow from the terminological use you're advocating, then there's not much more for me to say.
Aside from the meaninglessness I've shown...
Seems that there are brilliant people that have already shown the inherent issues in Set Theory, and they have done so on it's own terms... Russell comes to mind. Barbers and haircuts or something similar???
There are no empty sets. -
 Pfhorrest
4.6kIt sounds to me like you have no familiarity with set theory at all. Everything in mathematics is grounded in set theory, starting with empty sets. The natural numbers, for example, are constructed starting with the empty set, and then a set containing only that set, and then a set containing only those sets, and then a set containing all of those preceding sets, and so on. For any set S, the successor to S is the union of S and a set containing S. Operations can be constructed from set operations that relate sets in that set of sets of sets to each other in the same way that addition and multiplication relate natural numbers to each other, so that set of sets of sets is considered to be the natural numbers: the empty set is the number zero, the set containing it is the number one, the set containing both of those is the number two, and so on.
Pfhorrest
4.6kIt sounds to me like you have no familiarity with set theory at all. Everything in mathematics is grounded in set theory, starting with empty sets. The natural numbers, for example, are constructed starting with the empty set, and then a set containing only that set, and then a set containing only those sets, and then a set containing all of those preceding sets, and so on. For any set S, the successor to S is the union of S and a set containing S. Operations can be constructed from set operations that relate sets in that set of sets of sets to each other in the same way that addition and multiplication relate natural numbers to each other, so that set of sets of sets is considered to be the natural numbers: the empty set is the number zero, the set containing it is the number one, the set containing both of those is the number two, and so on.
This is standard mathematics, and the "terminological use I'm advocating" is standard logic. I'm not putting forward anything of my own here, I'm just trying to help you understand the normal way professionals on this subject understand things. -
creativesoul
12.2kI'm not denying that you're following convention. It is quite true that I have little understanding of philosophy of math(set theoryZFC) and/or higher maths. I would never attempt to imply otherwise. I was actually thinking about Cantor. I'm just conveying to you the issues that seem obvious to me concerning how talking about empty sets renders meaningful everyday easy to understand terms utterly meaningless.
You've said that that's the point.
You've also claimed that everything in mathematics is based upon set theory. That's utter bullshit. We were using maths long before, so...
While it may be true that current conventional understanding of maths employs set theory, it is quite simply not the case that all math is based upon set theory.
Math existed prior to. That which exists prior to something else cannot be existentially dependent upon that something else.
Anyway...
Yeah. So you're promoting conventional understanding. Good for you. -
 Pfhorrest
4.6kI said "grounded in". There have been long-standing questions about the foundations of mathematics, the current best answer to which is set theory. We often use higher-level things without knowing what lower-level things they're grounded in: we were breeding animals long before we know what genes were, for example.
Pfhorrest
4.6kI said "grounded in". There have been long-standing questions about the foundations of mathematics, the current best answer to which is set theory. We often use higher-level things without knowing what lower-level things they're grounded in: we were breeding animals long before we know what genes were, for example. -
creativesoul
12.2kI said "grounded in". — Pfhorrest
Grounded in... based upon...
As if there is a difference here that matters? You've already shown a penchant for rendering terms meaningless and/or incoherent. Now you're drawing distinctions that make no difference.
When something is grounded in something else it cannot exist prior to that something else. Math was prior to set theory. Math cannot be grounded in something that did not exist at the time we began using math.
We often use higher-level things without knowing what lower-level things they're grounded in: we were breeding animals long before we know what genes were, for example. — Pfhorrest
Here again, you've rendered otherwise meaningful terms incoherent and/or meaningless.
Following the above and applying it to the current discussion, math would be called "higher level" and set theory would be called "lower level". Set theory is far more complex than simple counting. So you're calling the more complex of the two "lower-level" and the most basic, rudimentary and foundational of the two "higher level".
Incoherent, meaningless, nonsense. -
creativesoul
12.2kSelective breeding was grounded in and/or was based upon attempting to acquire and/or retain specific characteristics/traits in offspring via choosing to breed individuals to each other that had those traits. It was not grounded in genes. That's preposterous. Our thought and belief about what sorts of characteristics/traits we would like to keep, and which ones we would like to not - all by selective breeding - could not be based upon or grounded in that which we had no knowledge of whatsoever.
Furthermore, the comparison itself is bogus. Genes existed in their entirety prior to our knowledge of them. Set theory did not. -
 Pfhorrest
4.6kYou miss the point of the analogy. Selective breeding works because of genetics, but we didn't need to know that in order to do it. We did it first, and later figured out why it works.
Pfhorrest
4.6kYou miss the point of the analogy. Selective breeding works because of genetics, but we didn't need to know that in order to do it. We did it first, and later figured out why it works.
Likewise, mathematics works for some reason or another, and that reason was in question for thousands of years, but we didn't need to know that in order to just add and stuff. We did that first, and only last century started coming up with strong rigorous explanations of why that stuff works, which explanations today universally rely on some kind of set theory. -
creativesoul
12.2kYou miss the point of the analogy. — Pfhorrest
No. You miss the following point:The analogy falls apart upon direct application to this discussion of ours. That's not the only one you've missed.
As already mentioned, you've exhibited a penchant for equivocation and/or incoherency.
You're calling higher level complexity things "lower", and lower level complexity things "higher". You're using the term "nothing" when referring to something. You're using the term "all" to refer to nothing.
This is the short list...
If this is what it takes in order to 'explain' how math works, then someone... somewhere... has gone horribly wrong. -
 Qmeri
2091. Zero (the mathematical 0) — TheMadFool
Qmeri
2091. Zero (the mathematical 0) — TheMadFool
The problem with "zero-nothing" is that, it always contains information in the sense that it is a limited possibility within all possibilities. If one considers limitations of what something can be information and considers that an existing thing then "zero-nothing" just means zero amount and not true nothingness. -
creativesoul
12.2kYou'll have to explain this supposed equivocation between "zero" and "nothing", because I'm not seeing what you're talking about. — Pfhorrest
You're still neglecting the facts here.
In order to have all of anything, there must be something to have. Something is not equivalent to nothing. Nothing is not all of something. Nothing is not all of anything.
You say:
You have zero out of zero, which is the most out of zero you could possibly have, i.e. all of it.
"All of it"???
"The most out of zero"???
:brow:
All of IT is all of something, because "it" always refers to something. Something is not equivalent to nothing. Yet, that is precisely how you've been employing the term "nothing". I said much earlier that it looked like an equivocation fallacy to me. Now, it's certain. It's not just weird. It's incoherent at best, and utter nonsense at worst. Either way, it's an equivocation of the terms "zero" and "nothing". That much is certain.
All meaningful use of "the most" presupposes "the least". "The most" makes no sense whatsoever unless there is also "the least". These two notions are both existentially and semantically dependent upon one another.
This is just plain old common sense.
"The most" and "the least" are always in direct inverse proportion to one another when dividing a whole into two unequal portions. That comparison gains complexity when dividing something into more than two unequal proportions, but the meaning of both "the most" and "the least" are still - and always are - established by comparison between a plurality of shares/portions/etc.
We talk about "the most" and "the least" after, and only after, we have something being dividing into a plurality of unequal (pro)portions. Otherwise, both notions are rendered utterly meaningless. There is no possible referent for either, unless there are referents for both.
And yet...
You've talked of "the most" of both nothing and zero, as if there is a meaningful quantitative difference to be drawn between the most of nothing and the least of nothing; as if there is a meaningful quantitative difference to be drawn between the most of zero and the least of zero.
There is not, and such talk is meaningless nonsense.
The most of zero is exactly the same as the least of zero. The most of nothing is exactly the same as the least of nothing. There is no distinction to be drawn here between the most of nothing(zero) and the least of nothing(zero) because they both have precisely the same numerical and/or quantitative value. — creativesoul
Do you care to answer these direct charges? Do you understand them?
Have I written the word "higher" when talking about things with far less complexity while simultaneously using the term "lower" to refer to other things with far more?
You're trying to convince me of the inductively sound nature of the logic of zero in terms of nothing when nothing means something, everything, and all.
I'm telling you that nowhere in your account have you explained the role that thought and belief play here. The discussion is skirting around the differences in our respective opinions concerning the type and amount of value that each of us places upon mathematical theory.
Numbers are names of quantities. Some of those quantities existed in their entirety prior to our naming them. Others... not so much. Which of the two are more basic, foundational, and/or simple?
Where does zero land? -
creativesoul
12.2kSaying "you have all zero of them" neglects the fact that in order to have all of anything requires that there first be something to have. Having all of something requires at least one thing. Zero things is not at least one thing. Zero things is nothing, and not in the same sense as when the term "nothing" is used as a means to pick out everything. — creativesoul
That gets at the heart of the equivocation of the term "nothing". -
TheMadFool
13.8kThe problem with "zero-nothing" is that, it always contains information in the sense that it is a limited possibility within all possibilities. If one considers limitations of what something can be information and considers that an existing thing then "zero-nothing" just means zero amount and not true nothingness. — Qmeri
What do you mean by that? How does zero contain information? -
TheMadFool
13.8kWhat is the correct antonym for nothing?
Something OR Everything OR <insert other alternatives>? — TheMadFool
Imagine a set, {dog, 9, $, F}.
If I remove 9, I have removed something but what I'm left with is {dog, $, F} which is still something and definitely not nothing.
If now I remove everything, I'm left with { }, the empty set aka nothing.
So, shouldn't the opposite of nothing be everything instead of something? :chin:
Now imagine that there's nothing, { }. Suppose {dog, 9, $, F} is everything. Now, I take 9 which is a something and add it nothing, it becomes {9} and nothing is no longer nothing. Shouldn't the opposite of nothing be something instead of everything? :chin:
Paradox alert! -
 Benj96
2.3k
Benj96
2.3k
If there was only black empty space it would be true nothing. Because there wouldn’t be something there to observe it as something. But you couldn’t even call it “nothing” because nothing to is as a word that has significance and indicates something. If you add something (mass-energy) then suddenly space is the “thing” that is not other things.
It is by contrast that things exist. No contrast, no polarity or dichotomy or pairs of extremes , then true nothing. But because energy is a spectrum there must stuff.
Just as zero is the same as -1 +1 energy time space and mass could simply be the property of true nothingness.
Or think of it as a double negative. Logically if “nothing” does not exist then something must exist.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum



