-
 SophistiCat
2.4kThat was a nice presentation and an interesting discussion. Thanks for putting in the effort!
SophistiCat
2.4kThat was a nice presentation and an interesting discussion. Thanks for putting in the effort!
I was thinking about what you said about the asymmetry of boundary conditions, e.g.
This does not put time and space on equal footing. The solution requires knowledge of u at one time and two places. These are generally derived from physical considerations, e.g. where the electron wavefunction must vanish: two positions where the wavefunction is zero at one time: generally the start. — Kenosha Kid
[The relativistic wavefunction] puts time and space on equal footing (both energy and momentum are squared), requiring knowledge of the particle at two times, not just one. This is why in relativistic quantum theories, we do not proceed by specifying an initial state, time-evolving it forward, and asking the probability of spontaneously collapsing to a particular final state. Rather, we have to specify the initial and final states first, then ask what the probability is. — Kenosha Kid
The true boundary conditions — Kenosha Kid
Mathematically, of course, any consistent set of boundary conditions is on equal footing with any other. And in any case, rather than solving a boundary value problem by time-evolving a wavefunction (forward and/or backwards), we can equivalently solve a least action problem, which obviates the question of where to start and where to end, since we are doing it everywhere at once. Which makes me wonder about the physical significance of all this, and particularly your main take-away about determinism.
The "trick" of putting some of the boundary conditions ahead in time makes the point a rather trivial one. Another way to state it would be to note that if there is a fact of the matter about the way the world is going to be at some future time, then there is nothing indeterminate about it. Well, of course.
I am also going to take a little issue with this:
This idea of the absolute square is important. It is how we get from the non-physical wavefunction to a real thing, even as abstract as probability. Why is the wavefunction non-physical? Because it has real and imaginary components: u = Re{u} + i*Im{u}, and nothing observed in nature has this feature. The absolute square of the wavefunction is real, and is obtained by multiplying the wavefunction by its complex conjugate u* = Re{u} - i*Im{u} (note the minus sign). Remembering that i*i = -1, you can see for yourself this is real. We'll come back to this. — Kenosha Kid
I wouldn't agree with the statement that the wavefunction is non-physical because it has a complex component. We can represent uncontroversially real entities with complex functions, as you are no doubt aware (e.g. the electromagnetic field in classical electrodynamics, and generally any 2D model where complex representation is expedient). Perhaps your thinking here is prompted by the QM formalism of observables - linear operators that, when applied to the wavefunction, produce real values that correspond to measurements (of position, momentum, and other attributes of a quantum state). But if only measurements are real, then nothing about the wavefunction as such is real, not even its absolute square: a probability density is not a measurement.
Anyway, this is probably a diversion (or not - you tell me). I myself don't regard the question of what there is as important. I take a theory as a whole, with all its ontological furniture, as real (enough) to the extent that it does a good (enough) job. -
 Harry Hindu
5.9k
Harry Hindu
5.9k
Then either QM is flawed in how it goes about showing that an electron is a wave, or your summarization of QM is flawed. I never asserted that electrons are or are not waves, merely that you didn't show that they were.The OP is not deriving QM, merely summarising it. Conversation would be pretty limited in scope if you have to re-derive from first principles everything that you intend to discuss every time. — Kenosha Kid -
 Kenosha Kid
3.2kThat was a nice presentation and an interesting discussion. Thanks for putting in the effort! — SophistiCat
Kenosha Kid
3.2kThat was a nice presentation and an interesting discussion. Thanks for putting in the effort! — SophistiCat
Thank you for saying so :)
The "trick" of putting some of the boundary conditions ahead in time makes the point a rather trivial one. Another way to state it would be to note that if there is a fact of the matter about the way the world is going to be at some future time, then there is nothing indeterminate about it. Well, of course. — SophistiCat
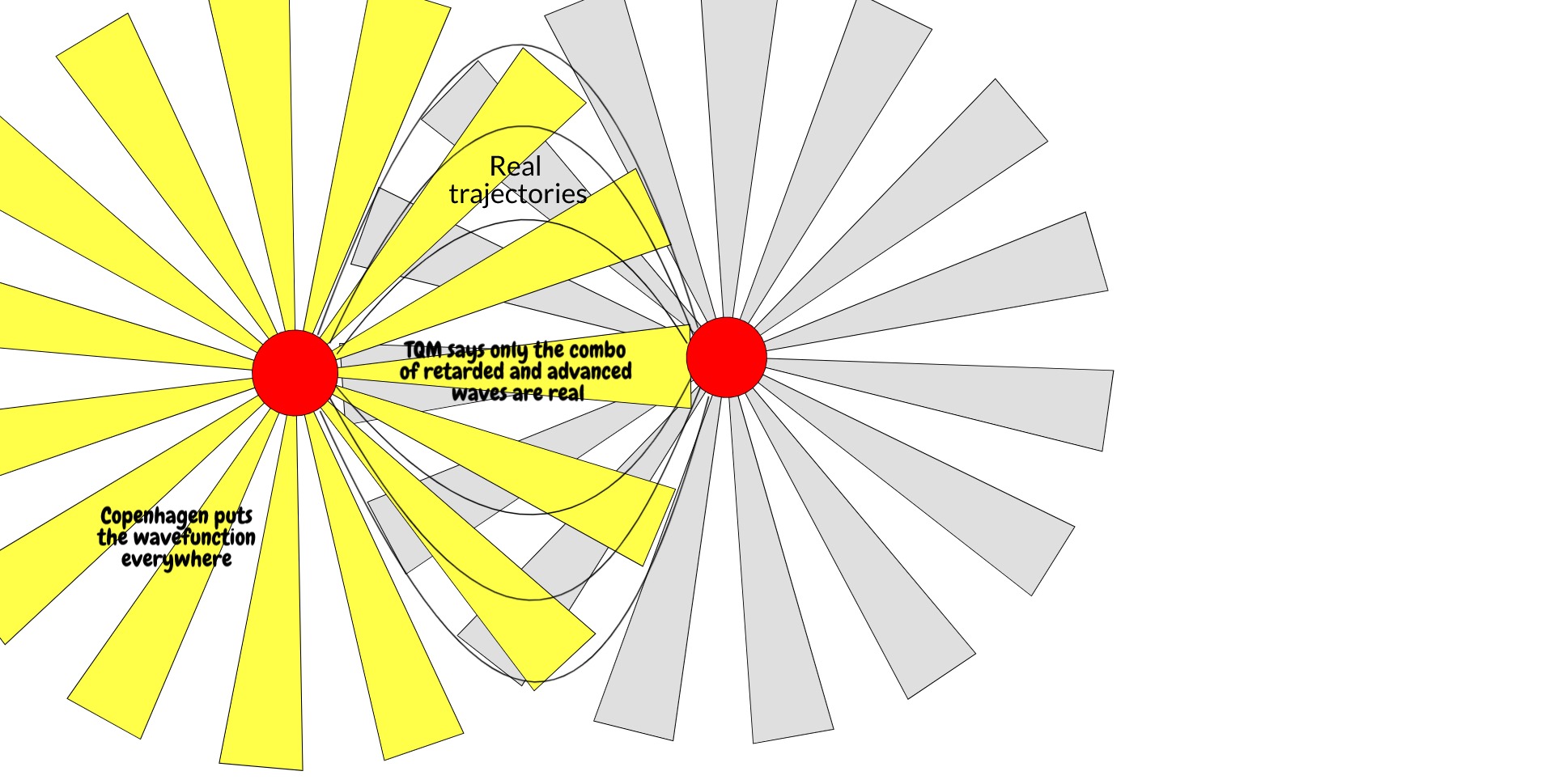
In the simple symmetric Minkowski spacetime, yes, it is trivial, and I think that's fdrake's point too. If the idea isn't controversial and the resultant determinism is trivially derived, I will take an "Of course!" But as I said to fdrake, transactional QM itself is still probabilistic. It removes the irreversible wavefunction collapse but which hole will be sent back is still undetermined. The last two images in the OP are essentially a recourse to other physical considerations leading to a conclusion that non-determinism is a case of running away with ourselves.
But the really good question here is the idea of boundary conditions as a "trick". You're right, we can do this in non-relativistic QM too. We'd essentially be forcing a final-state--dependence by hand, mimicking what is justified in the Dirac equation with what is not needed in the Schrödinger equation. My argument here is that the form of the equation is physically meaningful, i.e. the choice of boundary conditions is not just efficacious. The Copenhagen interpretation derives from the allowance to calculate wavefunctions from an initial state only because it's an approximation to reality, and it is this feature that yields wavefunction collapse and its inevitable probabilism. But this isn't real.
I wouldn't agree with the statement that the wavefunction is non-physical because it has a complex component. We can represent uncontroversially real entities with complex functions, as you are no doubt aware (e.g. the electromagnetic field in classical electrodynamics, and generally any 2D model where complex representation is expedient). — SophistiCat
But these aren't physical either. It is simply that complex exponentials are much easier to manipulate than individual sines and cosines. I'm not trying to do the wavefunction down, though. Whatever its ontology, it is important for predicting experimental outcomes and therefore corresponds to something physical. But no complex quantity can be physical in itself, i.e. we can't observe it in nature.
But if only measurements are real, then nothing about the wavefunction as such is real, not even its absolute square: a probability density is not a measurement. — SophistiCat
That's actually not an uncontroversial statement. The wavefunction is frequently referred to epistemologically as the total of our knowledge about a system. The OP basically states that it encoded more ignorance than knowledge.
Anyway, this is probably a diversion (or not - you tell me). — SophistiCat
No, all good points, especially about the "trick" of boundary conditions. -
 Kenosha Kid
3.2kThen either QM is flawed in how it goes about showing that an electron is a wave, or your summarization of QM is flawed. I never asserted that electrons are or are not waves, merely that you didn't show that they were. — Harry Hindu
Kenosha Kid
3.2kThen either QM is flawed in how it goes about showing that an electron is a wave, or your summarization of QM is flawed. I never asserted that electrons are or are not waves, merely that you didn't show that they were. — Harry Hindu
Again, I was not aiming to re-derive QM from scratch. If you want to know more about why individual electrons are waves, you can Google it. -
 Kenosha Kid
3.2kIs quantum theory the "set theory" of physics? Weird at first but providing a foundation? :chin: — jgill
Kenosha Kid
3.2kIs quantum theory the "set theory" of physics? Weird at first but providing a foundation? :chin: — jgill
Quantum field theory is the most foundational theory we have, underpinning everything we know about except gravity. It might be that QFT can be generalised to curved spacetimes but it's probably more likely that there's a more fundamental theory out there somewhere, something like string theory maybe. Check out Kakuza-Klein theory for why string-type theories are expected: https://en.wikipedia.org/wiki/Kaluza%E2%80%93Klein_theory?wprov=sfla1 -
 Metaphysician Undercover
14.8kBut let's turn the question around. An atom in the oven emits a photon and later another atom absorbs it and re-emits it (more like A below). How does the first atom know to emit a photon such that an even number of its wavelengths will fit in the box? How does either the atom or the photon know how big the box is? Photon emission is just the de-excitation of an atom from one energy level to a lesser one, and the energy of the oven is given by its temperature, which could be anything. — Kenosha Kid
Metaphysician Undercover
14.8kBut let's turn the question around. An atom in the oven emits a photon and later another atom absorbs it and re-emits it (more like A below). How does the first atom know to emit a photon such that an even number of its wavelengths will fit in the box? How does either the atom or the photon know how big the box is? Photon emission is just the de-excitation of an atom from one energy level to a lesser one, and the energy of the oven is given by its temperature, which could be anything. — Kenosha Kid
Do you think that a hot object knows that the cooler object is cooler when it radiates heat? Of course you do not, because you know that thermodynamic equilibrium, which determines whether emission occurs or not, is a feature of the object's relationship with its environment. And I'm sure you know that the definition of "black-body" is based in thermodynamic equilibrium. Since this idea which you have (I should call it an "ideal") that emission/absorption is reversible, is dependent on black-body conditions, it's practical significance is very limited.
Let's see if I can determine its significance. Emission/absorption is only reversible when an object is at thermodynamic equilibrium, which is when emission will not occur. When emission does occur, the object is not at thermodynamic equilibrium. Therefore emission/absorption is never reversible. However, we do have a slight issue, which is "black body emission". Of course this anomaly indicates that the ideal is faulty.
The question becomes less mysterious when we treat time and space equally: the emitted photon doesn't just have a spatial endpoint, but a temporal one, i.e. the photon can only be emitted when it "knows" where and when it will be absorbed. But how could this be? — Kenosha Kid
All radiation, other than black body radiation (which is an anomaly produced by misconception), is a feature of the relationship between the emitting body and its environment. There is no need to employ this type of imagery, such as the emitting body "knows" its environment.
Run that movie backwards and you have exactly the same thing... — Kenosha Kid
Clearly you cannot "run the movie backward". The idea that you can take an object's radiation of energy to its surroundings, and turn it around such that you can represent it as it's environment radiating the energy to the object, is completely unjustified, and obviously wrong.
The Copenhagen description, though, is irreversible: wavefunction collapse is a loss of information that is not retrieved by simulating the reverse process. — Kenosha Kid
Have you ever heard of "mechanical efficiency"? Mechanical efficiency is always less than 1, because a mechanical system always loses energy to its environment, friction for example. Clearly, we cannot have a reversal process, because energy is lost. We all know that perpetual motion is nonsense. It's covered by the second law of thermodynamics. Therefore you ought to know that your proposal of reversal is ridiculous. -
 Kenosha Kid
3.2kDo you think that a hot object knows that the cooler object is cooler when it radiates heat? — Metaphysician Undercover
Kenosha Kid
3.2kDo you think that a hot object knows that the cooler object is cooler when it radiates heat? — Metaphysician Undercover
That would be unnecessary according to the OP. It is sufficient that each particle knows where it is going. The statistical emergence of thermodynamics would arise from the fact that trajectories from (r,t) to (r',t) are more probable than their reverse. Indeed, all of thermodynamics is derivable from QM (via statistical mechanics: in fact, that's how we were taught stat mech at my uni), without any notion of heat being forced in by hand.
And I'm sure you know that the definition of "black-body" is based in thermodynamic equilibrium. — Metaphysician Undercover
No, a blackbody radiator is a non-equilibrium thermodynamic system, that is: it is not in equilibrium with its environment. An oven is something that radiates in its interior. So it's the interior radiation that is in equilibrium. The oven as a whole is still non-equilibrium.
Since this idea which you have (I should call it an "ideal") that emission/absorption is reversible, is dependent on black-body conditions, it's practical significance is very limited. — Metaphysician Undercover
Again, the CPT (charge-parity-time) symmetry of quantum field theory is not a new idea of my own that I'm presenting for consideration. It is a known symmetry that is broken by a few rare processes. I'll give you a heads up now, since you keep making this error: very little of what I've presented in the OP is original. The new-ish bits are that a) one cannot draw conclusions about where a particle may be found at a given time by considering only that particle at the time, and b) that the birth and death of a particle are its true boundary conditions. Those might be considered novel or controversial.
Emission/absorption is only reversible when an object is at thermodynamic equilibrium, which is when emission will not occur. — Metaphysician Undercover
At thermodynamic equilibrium, the rate of emission equals the rate of absorption (clue's in the name).
Clearly you cannot "run the movie backward". The idea that you can take an object's radiation of energy to its surroundings, and turn it around such that you can represent it as it's environment radiating the energy to the object, is completely unjustified, and obviously wrong. — Metaphysician Undercover
That's precisely what a system in equilibrium with its surroundings does. But I was discussing fundamental processes, not statistical ones. Fundamentally, a particle moving from one position to another is reversible for instance, e.g. things are not constrained to move in the same direction along a given axis.
Have you ever heard of "mechanical efficiency"? Mechanical efficiency is always less than 1, because a mechanical system always loses energy to its environment, friction for example. — Metaphysician Undercover
Thermodynamics does not demonstrably lead to loss of information. In fact, conservation of information and entropy are related. -
 fdrake
7.2kAnother self indulgent spitball from me. Thank you for the free physics lessons.
fdrake
7.2kAnother self indulgent spitball from me. Thank you for the free physics lessons.
But these aren't physical either. It is simply that complex exponentials are much easier to manipulate than individual sines and cosines. I'm not trying to do the wavefunction down, though. Whatever its ontology, it is important for predicting experimental outcomes and therefore corresponds to something physical. But no complex quantity can be physical in itself, i.e. we can't observe it in nature. — Kenosha Kid
What stops complex quantities from being physical? -
 Kenosha Kid
3.2kAnother self indulgent spitball from me. Thank you for the free physics lessons. — fdrake
Kenosha Kid
3.2kAnother self indulgent spitball from me. Thank you for the free physics lessons. — fdrake
I think you're doing okay without me, dude :D
What stops complex quantities from being physical? — fdrake
It's a good question. We certainly don't measure something as having a complex value, which could be a cognitive or technological limitation. It might be that the wavefunction is a 'real' (existing) thing and we encode our ignorance about its underlying nature as a complex phase (e.g. a compact dimension).
Or it might just be a mathematical trick, like Cat's examples. According to the Hohenberg-Kohn and Runge-Gross theorems (and, um, the me theorem), the wavefunction is uniquely given by the charge and current density and the environmental fields, all real-valued. We just don't have a good way of dealing with these quantities directly: wavefunctions are easier.
My take in the OP is that the wavefunction has some kind of existence and the real-valued densities arise from considering retarded and advanced waves. I wouldn't go as far as saying that the complex wavefunction is an accurate depiction even within this quite literalist view. -
 Kenosha Kid
3.2kP.S. I happened across this entire book on arxiv: https://arxiv.org/abs/1611.02738
Kenosha Kid
3.2kP.S. I happened across this entire book on arxiv: https://arxiv.org/abs/1611.02738
You would have thought that a book on the ontology of the wavefunction would examine the question of its complex nature, but nope. The word 'complex' appears a total of 9 times, one of which is in its everyday sense. It's entire insight on this question is: Schrödinger was surprised.
But it did jog my memory. The wavefunction can be written as a real function multiplied by a complex phase defined everywhere (this is trivial: a complex number has magnitude and phase). The phase is important for interference effects, but makes no difference when it comes to observables. The former is why I believe in an ontic wavefunction, and the latter is why the wavefunction might be considered epistemic.
Also, that complex phase function is directly related to the probability current, while the real part is directly related to the probability density. In fact, a single-particle wavefunction can be written as , where n is probability density and j is probability current. I'm not sure that's ever been published... It was on my whiteboard for years but never made it into a paper.
Now recalling the four-current from relativity, we have . (In tensor formulations we write the elements as real and move the imaginary part into the metric.) Again we see this relationship between a real spatial part and an imaginary momentum part, even without quantum mechanics.
So I'd venture that the complex nature of the wavefunction is to do with the relationship between space and time. It might not be something about the particle itself, but rather how we describe particles in space and time. -
 Kenosha Kid
3.2kP.P.S. If you're wondering about the half, that comes from the Schrödinger equation being a non-relativistic approximation. Energy is proportional to half the momentum squared in Schrödinger/Newton, while the square of the energy is proportional to the square of momentum in Dirac/Einstein. I never did the derivation for the Dirac equation, probably should.
Kenosha Kid
3.2kP.P.S. If you're wondering about the half, that comes from the Schrödinger equation being a non-relativistic approximation. Energy is proportional to half the momentum squared in Schrödinger/Newton, while the square of the energy is proportional to the square of momentum in Dirac/Einstein. I never did the derivation for the Dirac equation, probably should. -
 Metaphysician Undercover
14.8kIt is sufficient that each particle knows where it is going. — Kenosha Kid
Metaphysician Undercover
14.8kIt is sufficient that each particle knows where it is going. — Kenosha Kid
That's nonsense, to say that a particle knows where it's going. Are you suggesting that the particle has a mind of its own? And it's really no different from my example of saying that the hot object knows where the cold object is. All you are doing is qualifying this to say it's not really the hot object which knows where the cold object is, it's the energy within the hot object which knows where the cold object is.
It's not the case that the particle knows where it is going. What is the case, as I explained in my earlier post, is that the human conception of radiant energy is based in the absorption of energy, because it is empirically based. As I said, "we can talk about something radiating energy into empty space, into an infinite vacuum or some such thing, but this is not consistent with the concept which is based in objects receiving energy, not in objects emitting energy." It's not the case that the energy transmitted must know where it's going, what is the case is that we do not have the understanding which is required to conceptualize radiant energy in any way other than through the empirical observations of absorption. Emission is simply a logical extension of that conception. Then you find some axioms which state that emission is the reverse of absorption, and so be it, in your mind. Despite all the obvious evidence that it is not.
Even the idea that there is a particle which is transmitted is unsupported by evidence. The emitting object has a field. There are waves between the emission and the absorption. That there is a particle which is emitted cannot be empirically verified. Whatever it is which is emitted (waves I am told by physicists), cannot be directly observed without being absorbed. Therefore your logical conclusion, that there is a particle which is emitted is simply a product of your desire to represent emission as the reverse of absorption. You are begging the question. Emission is the reverse of absorption, a particle is absorbed, therefore a particle is emitted. But the evidence is contrary to this, because all that is observable between the emitting and the absorption, is wave patterns. So you have absolutely no justification for the claim of a continuously existing particle being emitted from one location, and being absorbed at another. I would stress that you appear to have a desire to represent emission as the reverse of absorption, so you theorize that there is a continuously existing particle in between, to support this theory. But the empirical evidence clearly suggests otherwise.
No, a blackbody radiator is a non-equilibrium thermodynamic system, that is: it is not in equilibrium with its environment. — Kenosha Kid
Yes, but being "non-equilibrium", means that it is based in the concept of equilibrium. Which is what I said, even if you didn't interpret it that way.
I'll give you a heads up now, since you keep making this error: very little of what I've presented in the OP is original. — Kenosha Kid
Yes, I realize that, I've come across most of what you have written here in researching my replies to you. Do you get most of your information from Wikipedia? You ought to pay more attention to respected physicists instead. Someone like Dr. Feynman for example describes energy transmission as waves, not as particles. Your idea that a particle moves from emission to absorption, though it might make interesting discussion on the internet, is not really accepted by mainstream physics. That's why the in between is represented by a wave function. I'm sure you are aware of the fact that the wave function is not meant to represent the continuous existence of a particle. It is meant to predict where a "particle" (or whatever it is which bears that name) might appear.
Fundamentally, a particle moving from one position to another is reversible for instance, e.g. things are not constrained to move in the same direction along a given axis. — Kenosha Kid
Sure, a particle moving from one place to another is reversible. But physicists tell us that electromagnetic energy moves from one place to another as waves, regardless of what pseudo-scientists on the internet are saying. So this is the difficulty you need to overcome in order to have your theory even considered. It might be considered by people who don't know fundamental principles of physics, and think that electromagnetic radiation is transmitted as particles, but physicists know that transmission is through waves. -
 jgill
4kThat's nonsense, to say that a particle knows where it's going. Are you suggesting that the particle has a mind of its own? — Metaphysician Undercover
jgill
4kThat's nonsense, to say that a particle knows where it's going. Are you suggesting that the particle has a mind of its own? — Metaphysician Undercover
If a substantive thing, (massive object), is inclined toward temporal continuity (as inertia implies), yet "feels" a force which would impel that object to change, then there are two very distinct forces involved, the force to stay the same, and the force to change. If the object stays the same, despite feeling the force which would impel it to change, doesn't this appear to you like the object has made a choice, and exercised will power to prevent the force of change? — Metaphysician Undercover -
 Kenosha Kid
3.2kDo you get most of your information from Wikipedia? — Metaphysician Undercover
Kenosha Kid
3.2kDo you get most of your information from Wikipedia? — Metaphysician Undercover
No, I did something that has apparently never occurred to you: I got an education. -
 SophistiCat
2.4kAs I read your reply I realized that I didn't really understand the OP :confused: So let me try another question to see if that helps a bit: How does your (transactional?) interpretation recover the Born rule? How do you get the interference stripes in the double slit experiment? Unless I misunderstood again, it seems like you were saying that real-world constraints (availability of holes, etc.) should cut down on indeterminism and perhaps completely eliminate it in the limit. But then we have to believe that these constraints just happen to conspire to produce results consistent with the probability distribution?
SophistiCat
2.4kAs I read your reply I realized that I didn't really understand the OP :confused: So let me try another question to see if that helps a bit: How does your (transactional?) interpretation recover the Born rule? How do you get the interference stripes in the double slit experiment? Unless I misunderstood again, it seems like you were saying that real-world constraints (availability of holes, etc.) should cut down on indeterminism and perhaps completely eliminate it in the limit. But then we have to believe that these constraints just happen to conspire to produce results consistent with the probability distribution?
But these aren't physical either. It is simply that complex exponentials are much easier to manipulate than individual sines and cosines. — Kenosha Kid
Well, exactly. You can reproduce all complex-valued math without recourse to imaginary numbers or complex exponentials - it would just be more work. But then I don't understand why you insist that
But no complex quantity can be physical in itself, i.e. we can't observe it in nature. — Kenosha Kid
Complex quantities are no more and no less physical than real quantities, tensors, vectors, and whatnot. They are all mathematical objects.
That's actually not an uncontroversial statement. The wavefunction is frequently referred to epistemologically as the total of our knowledge about a system. The OP basically states that it encoded more ignorance than knowledge. — Kenosha Kid
he wavefunction can be written as a real function multiplied by a complex phase defined everywhere (this is trivial: a complex number has magnitude and phase). The phase is important for interference effects, but makes no difference when it comes to observables. The former is why I believe in an ontic wavefunction, and the latter is why the wavefunction might be considered epistemic. — Kenosha Kid
Sorry, you seem to be making a distinction without a difference here. Both the amplitude and the phase are essential for encoding our knowledge about the system. So if that makes the wavefunction real in a broad sense (which is fine by me), then the whole of it has to be real, not just the amplitude. -
 Harry Hindu
5.9kNo, I did something that has apparently never occurred to you: I got an education. — Kenosha Kid
Harry Hindu
5.9kNo, I did something that has apparently never occurred to you: I got an education. — Kenosha Kid
Looks more like you got an indoctrination, a process of teaching a person or group to accept a set of beliefs uncritically.
Any theory that doesnt attempt to explain the role of the observer/measurer in an event involving observation/measurement is missing half of the explanation, especially when we observe changing measuring devices changes the observed outcome. -
 Kenosha Kid
3.2kHow does your (transactional?) interpretation recover the Born rule? — SophistiCat
Kenosha Kid
3.2kHow does your (transactional?) interpretation recover the Born rule? — SophistiCat
From the overlap integral of the retarded wavefunction with the advanced wavefunction:
In transactional QM, this is the very meaning of the Born rule. It's not my transactional QM btw, it's been around a while I think.
How do you get the interference stripes in the double slit experiment? — SophistiCat
When a particle moves from event (r,t) to (r',t'), it still does so by every possible path (Feynman's sum over histories). If you sum up every possible r' at t' and normalise, you recover the wavefunction at t'.
Complex quantities are no more and no less physical than real quantities, tensors, vectors, and whatnot. They are all mathematical objects. — SophistiCat
Ah, I see. This is deeper than I'd realised. Simply multiply whatever complex number by whatever physical unit: we never see that. I see I have 10 fingers and that I'm 5.917 feet tall, but I have never weighed (12 + 2i) stone.
So if that makes the wavefunction real in a broad sense (which is fine by me), then the whole of it has to be real, not just the amplitude — SophistiCat
I'm getting confused now between ontologically real and real as in has no imaginary component. I started it, mea culpa. I'll rephrase.
The OP holds that the complex wavefunction is an ontic description -- or fair approximation to such -- of how particles propagate through space and time as we represent them. How we describe the relationship between time and space is intrinsically complex, just from straight relativistic vector calculus, which happens to be the language quantum field theory is written in. There are other languages for describing relativity that can do away with the imaginary number and it may well be that in future we can generalise QFT in a similar way; such an endeavour would be part of a general relativistic quantum mechanics. So I don't hold the complex wavefunction to be an ontic description of the particle itself, rather it encodes the ontology of the wavefunction in our spacetime representations accurately, e.g. encodes information vital for doing the physics. -
 Harry Hindu
5.9kThere is no cutoff, which is fine as I am not exploring the realm of the classical limit. It is sufficient to know that a classical limit exists. The relevance of the macroscopic screen is merely that it explores microstates, nothing more. — Kenosha Kid
Harry Hindu
5.9kThere is no cutoff, which is fine as I am not exploring the realm of the classical limit. It is sufficient to know that a classical limit exists. The relevance of the macroscopic screen is merely that it explores microstates, nothing more. — Kenosha Kid
Yet the screen, double slits and the electron emitter are all macro objects composed of electrons and all have an effect on the outcome of the experiment.The back screen is a macroscopic object that cannot be treated precisely with quantum mechanics — Kenosha Kid
Looks like QM has limits as well.
We only conceived of atoms in order to explain observations of macro-sized objects and QM was conceived of to explain the behavior of atomic sized objects. Seems to me that if the theories were compatible they would seamlessly integrate, like genetics and evolution (micro vs macro explanations of the same process).
Why would there be limitations if this is suppose to be a theory explaining the fundamentals of reality, if it's not that both classical and QM are explaining different views/measurements of the same thing? -
 Metaphysician Undercover
14.8k
Metaphysician Undercover
14.8k
The second quote you have taken out of context, and the reference link does not link to the context. Notice that I have "feels" in quotation marks, because this was not my terminology, and I was criticizing this way of describing the situation.
The same criticism is applicable here too though. If the electromagnetic field, through which radiation transmits, extends from one object to another, and there is energy which is received at the other, but not enough to cause a physical effect (i.e. not enough for the object to absorb a photon of energy by photoelectric effect), then if we are using that terminology which KK chooses to use, you might say that the object "feels" the other, without being physically affected by it. If this were really the case, then we ought to conclude that the second object exercises will power to prevent itself from being physically affected by the other, because this is the only reasonable way that we have to talk about one object being affected by another, without causing a physical change. By the precepts of physics, if one object affects another, there is necessarily a change to the other, or else we cannot say that the one affects the other, because that claim would be unsupported by empirical evidence, and physics does not accept panpsychism as providing reasonable explanatory principles.
No, I did something that has apparently never occurred to you: I got an education. — Kenosha Kid
As evident from the terminology which you use, (described in my reply to jgill above), your education was not in physics. Nor was mine, so we ought to be on par for any approach to this matter of physics.
The OP holds that the complex wavefunction is an ontic description -- or fair approximation to such -- of how particles propagate through space and time as we represent them. — Kenosha Kid
This is where you're wrong, and you ought to refer to some real physics to sort yourself out. There are many true statements one can make about "the wavefunction", but the wavefunction does not describe the propagation of particles through space and time. That is a false proposition. We can say that the wave function may be used to predict where a particle will appear, through a description of the propagation of energy (as wave motion), but we cannot conclude that it describes the propagation of particles. It really describes the propagation of waves, hence "wave" function. -
 SophistiCat
2.4kFrom the overlap integral of the retarded wavefunction with the advanced wavefunction:
SophistiCat
2.4kFrom the overlap integral of the retarded wavefunction with the advanced wavefunction:
In transactional QM, this is the very meaning of the Born rule. — Kenosha Kid

But this only gives the "real paths" of the electron once the "boundary condition" on the other end is fixed, i.e. once the measurement already happened at the back screen. This doesn't explain any actual data though: we have no independent knowledge of those "real paths" besides what the interpretation tells us. What we have from experimental setup and observation are just the boundary conditions, the origins of the retarded and the advanced wavefunctions. And while we fix the former by our setup, all we know about the latter in advance is:
When a particle moves from event (r,t) to (r',t'), it still does so by every possible path (Feynman's sum over histories). If you sum up every possible r' at t' and normalise, you recover the wavefunction at t'. — Kenosha Kid
which is no more than what vanilla QM tells us and doesn't explain the really interesting bit, i.e. the measurement problem. And isn't that what we really want from an interpretation?
So what mechanism fixes the forward boundary condition?
Ah, I see. This is deeper than I'd realised. Simply multiply whatever complex number by whatever physical unit: we never see that. I see I have 10 fingers and that I'm 5.917 feet tall, but I have never weighed (12 + 2i) stone. — Kenosha Kid
Well, of course, if you take something that is usually represented by a scalar, such as height or weight, then a real number will be optimal as a mathematical representation. But take something like stress, for example, and you'll want a tensor or a vector at the least. (Although if you really set your mind to it, you can map a quantity of any dimensionality to any other dimension. You can map 6-tuples to scalars and back - it'd just be horribly impractical.)
I'm getting confused now between ontologically real and real as in has no imaginary component. — Kenosha Kid
Yeah, I suspected as much.
The OP holds that the complex wavefunction is an ontic description -- or fair approximation to such -- of how particles propagate through space and time as we represent them. How we describe the relationship between time and space is intrinsically complex, just from straight relativistic vector calculus, which happens to be the language quantum field theory is written in. There are other languages for describing relativity that can do away with the imaginary number and it may well be that in future we can generalise QFT in a similar way; such an endeavour would be part of a general relativistic quantum mechanics. So I don't hold the complex wavefunction to be an ontic description of the particle itself, rather it encodes the ontology of the wavefunction in our spacetime representations accurately, e.g. encodes information vital for doing the physics. — Kenosha Kid
Fair enough. -
 jgill
4kAs evident from the terminology which you use, (described in my reply to jgill above), your education was not in physics. Nor was mine, so we ought to be on par for any approach to this matter of physics — Metaphysician Undercover
jgill
4kAs evident from the terminology which you use, (described in my reply to jgill above), your education was not in physics. Nor was mine, so we ought to be on par for any approach to this matter of physics — Metaphysician Undercover
It would help if this issue is clarified. -
 Kenosha Kid
3.2kBut this only gives the "real paths" of the electron once the "boundary condition" on the other end is fixed, i.e. once the measurement already happened at the back screen. — SophistiCat
Kenosha Kid
3.2kBut this only gives the "real paths" of the electron once the "boundary condition" on the other end is fixed, i.e. once the measurement already happened at the back screen. — SophistiCat
Yes. I think your question was: how do we get the Born rule? The Born rule is derived from each retarded path in the sum over histories overlapping with each advanced, conjugate path coming back from the screen. The Born rule would only apply to the real paths.
This doesn't explain any actual data though: we have no independent knowledge of those "real paths" besides what the interpretation tells us. What we have from experimental setup and observation are just the boundary conditions, the origins of the retarded and the advanced wavefunctions. — SophistiCat
True, but this is actually a more minimalistic interpretation of empirical data. It yields a single position on the back screen without magical collapse mechanisms or (hopefully) proliferating universes, and still yields the same interference effects as standard QM interpretations.
TQM, Copenhagen, MWI, Bohm etc. are all obliged to yield the same experimental predictions, having the same mathematics. The point here is more that the philosophical ramifications of an ideal screen in Copenhagen are naive, and that the fact that complex conjugates of solutions to the Dirac equation are also solutions to the Dirac equation, in fact the general idea that there's no obvious arrow of time in special relativity, does not support the assumption of such collosally irreversible and information-losing processes. There are more physically well-grounded and more rigorous approaches to understanding the same experimental data.
which is no more than what vanilla QM tells us and doesn't explain the really interesting bit, i.e. the measurement problem. — SophistiCat
There is possibly no measurement problem in this formulation, because the (numerically) real aspect of the wavefunction is never spread out across the screen. The electron travels from (r,t) to (r',t') by every possible path, but only to (r',t'). If you were to place a screen midway at r'', you wouldn't get the same paths, therefore no collapse.
It is, I think, impossible to prove that every path through every other possible value of (r',t') can be eliminated by considering the entire history and future of the electron (or, respectively, future and history of the hole(s) it overlaps with), hence the jokily-named not-many-worlds interpretation. But conversely it's impossible to prove that the electron does actually have a real probability to be found at any point on the screen. The former is simpler, however, and it is possible to state with absolute surety though that not every part of the screen is accessible that Copenhagen says is accessible.
Well, of course, if you take something that is usually represented by a scalar, such as height or weight, then a real number will be optimal as a mathematical representation. — SophistiCat
Well, the wavefunction is a scalar field :) -
 fdrake
7.2kRegarding the imaginary numbers can't be physical thing, and the problem being having an imaginary part.
fdrake
7.2kRegarding the imaginary numbers can't be physical thing, and the problem being having an imaginary part.
Complex numbers form a 2D vector space over the reals which is isomorphic to (vectors take the form (Re(z), Im(z), adding real and imaginary parts works just the same as adding x and y components, it's why the plane representation of complex numbers works).
Complex numbers as a field are isomorphic to a collection of 2 by 2 matrices.
If it's impossible for an imaginary quantity to be physical, and it's possible for a real quantity to be physical, why would it be the case that one complex number representation (x+yi) can't be physical, and another (2 by 2 matrices of real numbers) might be physical? I think that leads to three possibilities:
(1) The property "is physical" (or "is physically meaningful" or whatever) is not preserved by isomorphism of structures.
(2) Neither complex numbers nor real numbers can be physical.
(3) Both complex numbers and real numbers can be physical.
I find (1) implausible: all the mathematical properties of an algebraic structure are preserved over isomorphism, so whether something is physically meaningful or not would then have to depend on something extra-mathematical that somehow varies with an isomorphism. Could lead to situations where two models have all the same equations and experimental predictions but one is somehow physically meaningful and the other isn't.
I find (2) implausible: describing reality well is what good theories do. Assuming it leads to absurdities like while the concept of mass might be physical, the number associated with every mass measurement cannot be.
Left with (3). Though it's got quite a lot of work left to do in it. How "physical meaning" distributes over the components of a physical model is something I've wondered about since seeing geometric series infinite sums used in inelastic rebound; computing the infinite sum assumes an infinite amount of collisions with arbitrarily small bounces. But that's not a "physically meaningful" part of the model. -
 jgill
4kComplex numbers form a 2D vector space over the reals which is isomorphic to R2 (vectors take the form (Re(z), Im(z), adding real and imaginary parts works just the same as adding x and y components, it's why the plane representation of complex numbers works). — fdrake
jgill
4kComplex numbers form a 2D vector space over the reals which is isomorphic to R2 (vectors take the form (Re(z), Im(z), adding real and imaginary parts works just the same as adding x and y components, it's why the plane representation of complex numbers works). — fdrake
This might trivialize C. Here's a quote from the web, from an educational perspective:
"Question.Is C isomorphic to R2? Answer.As a what? A field?Question (revised).Is the field C isomorphic to the fieldR2?Answer.NO! R2is not a field, it’s a vector space!Question (re-revised).Is the vector space C isomorphic to the vector space R2?Answer.That’s a good question! However, it is meaningless/misleading. A vector space isomorphism is only defined between two vector spaces over the same field. R2 is a two dimensional field over R and C is a one dimensional vector space over
I.2."
Elementary dynamical systems in C I have worked on would not have been possible in R2. -
 fdrake
7.2kThis might trivialize C. Here's a quote from the web, from an educational perspective: — jgill
fdrake
7.2kThis might trivialize C. Here's a quote from the web, from an educational perspective: — jgill
A vector space isomorphism is only defined between two vector spaces over the same field — jgill
Aye. All the "i" is doing when thinking of C as a 2d vector space over R is keeping track of the second coordinate. It is an isomorphism of vector spaces over the reals, but not an isomorphism of fields. So in that respect, it might be misleading for me to have said that "the complex numbers form a 2d vector space" over R, because "the complex numbers" are a field. You and the quoted thing are right! My mistake.
I wrote a version of the post you responded to that only used that fact, but considered it too weak as it didn't respect the field structure. The second fact; the isomorphism of the field C with a field of 2 by 2 real matrices; I believe suffices for my point. -
 Metaphysician Undercover
14.8kIt would help if this issue is clarified. — jgill
Metaphysician Undercover
14.8kIt would help if this issue is clarified. — jgill
My guess is that KK is an engineer. -
 Kenosha Kid
3.2kIf it's impossible for an imaginary quantity to be physical, and it's possible for a real quantity to be physical, why would it be the case that one complex number representation (x+yi) can't be physical, and another (2 by 2 matrices of real numbers) might be physical? — fdrake
Kenosha Kid
3.2kIf it's impossible for an imaginary quantity to be physical, and it's possible for a real quantity to be physical, why would it be the case that one complex number representation (x+yi) can't be physical, and another (2 by 2 matrices of real numbers) might be physical? — fdrake
We've never managed to measure anything that is a 2x2 matrix either. We use matrices a lot -- they are useful, but they are constructs. I don't think nature knows about them.
What I think is a better criterion is whether we can do without them. Negative numbers are empirically indispensable, interference effects being a great example, electric charge being another. Complex numbers may also be indispensable, or they might just be efficacious. Given the way they enter into the equations, my feeling is that it's the latter, but I'm not trying to make that particular case in the OP. However complex things are at root, empirically they manifest as real. -
 fdrake
7.2kFeel free to ignore or take this to PMs if you believe this is too much of a side issue @Kenosha Kid.
fdrake
7.2kFeel free to ignore or take this to PMs if you believe this is too much of a side issue @Kenosha Kid.
We've never managed to measure anything that is a 2x2 matrix either. We use matrices a lot -- they are useful, but they are constructs. I don't think nature knows about them. — Kenosha Kid
Very skeptical of that. Whether a quantity can be physical or not should not depend on how it is recorded. Somehow individual measurements are physical but tabulating them makes them incapable of being physical. Nature can "know" about the vector elements but not the vector? The matrix elements but not the matrix they constitute together?
Given the way they enter into the equations, my feeling is that it's the latter, but I'm not trying to make that particular case in the OP. However complex things are at root, empirically they manifest as real. — Kenosha Kid
"empirically manifesting as real" and "being physically meaningful" don't play so well together I think. Depends on how they're fleshed out.
EG: if the criterion for a theory (as a whole) being physical is successful prediction of experimental results ("manifesting as real"), it's silent on theory elements. A conception like that wouldn't let you intervene mid argument with a physical insight to conjecture a next step or ignore a class of solutions, since it doesn't constrain theory elements at all, only constraining theories' being "physical" as a whole by resultant predictions.
Or: if the criterion for a theory element being physically meaningful is simply that it is part of a theory which produces successful predictions, then the complex conjugated solutions are physical since they are part of the theory. But that also trivialises physical insight, as the criterion cannot distinguish between theory components as before.
Or: if the criterion for a theory element being physically meaningful requires that it is a measurable quantity, then only measurable quantities in theories can be physically meaningful - and that rules out the discussion item (as @SophistiCat implied with his observables comment).
From what I've seen, that is how physical meaning/the property "is physical" is used, to operate on steps mid argument, to rule out solution classes, to declare something a mathematical trick or not. A criterion that either makes all theory elements equally physical, does not care about theory elements at all, or requires that all concepts employed have measurable values can't suffice here.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Biological Determinism As The Fundamental Pedagogy of National Socialist Thought (Half of Chapter 1)
- Biological Determinism As The Fundamental Pedagogy of National Socialist Thought
- The Consequences of Belief in Determinism and Non-determinism
- Are we doomed to discuss "free will" and "determinism" forever?
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum






