-
 Benj96
2.3kPi is essentially an endless number (irrational)
Benj96
2.3kPi is essentially an endless number (irrational)
We require pi to construct a circle.
Pi to 1+ nth decimal places is a more accurate approximation of pi than simply pi to one place (3).
Therefore, is it impossible to create a perfect circle?
A circle made with 3.14159 is better than one made with 3.14 so by this logic a perfect circle has never nor will it ever be created. It seems ridiculous because we have observed seemingly perfect geometric circles and we all know what one looks like apparently. How can such a simple task be that impossible.
If we asked a computer to make a perfect circle it would begin by extracting an accurate pi which will take it eternity. Therefore the function cannot be done. It reminds me a little if Zenos paradox -
 ssu
9.8kThinking like that, would it be possible to make any perfect geometric drawing?
ssu
9.8kThinking like that, would it be possible to make any perfect geometric drawing?
Let's assume that you have draw a square that has exactly 10 cm sides. So not only 10,00 cm or 10,000000 cm, but with total accuracy to be exactly 10 cm. Again, you simply cannot do it.
Mathematical objects aren't limited by our physical limitations on what we can physically do in reality. -
 Benj96
2.3kMathematical objects aren't limited by our physical limitations on what we can physically do in reality. — ssu
Benj96
2.3kMathematical objects aren't limited by our physical limitations on what we can physically do in reality. — ssu
Interesting. Wouldn’t that mean that there’s no end point to increasing accuracy? If we suppose that perfection is reaching the point at which no further state of accuracy can be reached then everything we’ve ever done with maths is an approximation.
It’s a bit confusing because of the existence of rational and irrational numbers. 1 is what it is.. ..there is no “1” that is more accurate then another “1”. However as you correctly pointed out, the smaller we divide the number the more accurate it is. A measuring tool that can measure in mm is more accurate then one that measures centimetres. And one that measures in nanometers is again more accurate. Can this go on for ever? Surely there is a minimum?
Of course this requires spatial dimension/ distance. Without space (non physical maths) there is no need for this increasing division to get an accurate answer. 1 is ultimately arbitrary. Because in order to have 1 of anything we must somehow discern that it is different from its surroundings -
 Benj96
2.3kah. I see I have misunderstood the definition of irrational numbers.
Benj96
2.3kah. I see I have misunderstood the definition of irrational numbers.
Not so much whether it is infinite or not but whether it can be expressed as a fraction.
Okay so as for 1.33333’ I suppose the recurrent 3 is endless and so we could argue that we know that the number will be a 3 regardless of the decimal place.
But how do we know for sure? There’s no proofs we can do to determine if indeed it continues as 3 forever. It stands to logic that it does and we usually round it eventually to stop the recurrence but I just find it baffling that numbers are endless and yet we can still use them practically. We have no base lines - it’s all arbitrary. The standard by which we use maths is manufactured by ourselves. Our entire use of it is based on relationships and ratios between ultimately artificial symbols which go to explain the physical world very well but are themselves not intrinsic to it. Just useful make believe.
The second for example again is just a quantification of something that has no quantity - time. Then again, I suppose any biological system operates in quantities of molecule to discern rhythms and cycles and I guess therefore time.
The kingdom of life doesn’t have a watcher calendar like us yet they still make do quantifying time through the same ratios we use maths to figure out.
Did we acquire maths from nature and observation then or is maths a man-made convenience to describe the things we seen in nature? -
 fishfry
3.4kBut how do we know for sure? There’s no proofs we can do to determine if indeed it continues as 3 forever. — Benj96
fishfry
3.4kBut how do we know for sure? There’s no proofs we can do to determine if indeed it continues as 3 forever. — Benj96
Of course there is, it's the grade school division algorithm. Perhaps they no longer teach this. If you divide 3 into 1 using the procedure they used to teach when I rode a dinosaur to school, you'll see that you always get 3 for the next digit, so that the 3's are perfectly deterministic and predictable by, say, a computer program.
On the other hand ... so are the digits of pi. For example consider the famous Leibniz formula for pi:
We can express this famous series as a closed-form expression like this:
which, if I counted correctly, can be expressed in exactly 15 symbols.
In other words pi, just like 1/3, only encodes a finite amount of information; despite their respectively endless decimal representations.
The answer to this mystery is that it's the decimal representation itself that's flawed. Some real numbers have two distinct representations, as 1/2 = .5 = .4999...; and others have no finite representation.
There are in fact other ways of expressing real numbers, The takeaway here is not to get hung up on the deficiencies of decimal representation; but rather to focus on the actual information content of a real number. In particular, 1/3 and pi are each expressible by a finite-length computer program or description. For 1/3, it's the grade school division algorithm applied to 3 into 1; and for pi, it's the Leibniz formula, or any one of the many other closed-form finite-length expressions for pi.
As far as drawing a conceptual circle, if you simply plot all the points on the x-y plane that are a distance of 1 from the origin, you'll get a perfect mathematical circle of radius 1 and circumference 2 pi. We can't draw a perfect circle in the real world, but as others have noted, we can't draw any perfect geometric figure in the real world. Geometric figures are abstract conceptions of the mind. They either live in the Platonic world, if you believe in such a thing; or they're abstract inventions of humanity, if you don't.
1 is ultimately arbitrary. — Benj96
Excellent insight. If you take a straight line and mark two points: one called '0' and the other called '1'; you thereby define your unit length, and all other lengths are relative to those two arbitrary choices. -
 Benj96
2.3kwhen I rode a dinosaur to school, — fishfry
Benj96
2.3kwhen I rode a dinosaur to school, — fishfry
Lol. No we did learn it in school also. And I’ve never questioned it’s validity as it makes sense. I suppose what I’m getting it is there is a conflicting method by which we establish the “definite”.
One is “exhaustive” and the other is “predictive”.
What I mean by this is you can establish the determined nature of something by “getting to the root of it ie find the origin (exhaustive) or you can take a sort of shortcut (predictive) by finding a pattern and relying on the assumption that said pattern repeats indefinitely by virtue of being a pattern.
But the problem I had with pi is that it didn’t seem to follow a predictable pattern so the only other way to determine it in the absolute is the exhaustive method - which is an endless endeavour in said case.
But what I didn’t understand is this equation (leibniz) that reduces the seemingly random and infinite progression to just 15 variables has in fact made it “predictive”.
The case is settled. -
 fishfry
3.4kBut what I didn’t understand is this equation (leibniz) that reduces the seemingly random and infinite progression to just 15 variables has in fact made it “predictive”. — Benj96
fishfry
3.4kBut what I didn’t understand is this equation (leibniz) that reduces the seemingly random and infinite progression to just 15 variables has in fact made it “predictive”. — Benj96
Yes, in fact it was Turing who made the observation that numbers such as 1/3 and pi are computable; that is, their digits can be cranked out by a computer program or algorithm. There are in fact noncomputable real numbers, which are truly random.
On the other hand, the digits of pi are (as far as we know, but we're not sure) statistically random. They don't appear to follow any pattern, even though they are completely deterministic. The same is true of random() functions in programming languages. They produce a sequence of outputs that are statistically random, even though their underlying algorithms are completely deterministic.
So there are two different concepts: Actually random, and statistically random. There's a technical term for this distinction. A sequence that is statistically random but not necessarily actually random is called stochastic.
But I think your original concern is more about the impossibility of drawing perfect geometric figures in practice, rather than the subtleties of randomness. -
 TonesInDeepFreeze
3.8kThere’s no proofs we can do to determine if indeed it continues as 3 forever — Benj96
TonesInDeepFreeze
3.8kThere’s no proofs we can do to determine if indeed it continues as 3 forever — Benj96
No, it is proven.
We have no base lines - it’s all arbitrary. — Benj96
Perhaps you might say that the axioms are arbitrary. But, given the axioms, proof that some reals have infinite decimal expansions is definite. -
 TonesInDeepFreeze
3.8krelying on the assumption that said pattern repeats indefinitely by virtue of being a pattern. — Benj96
TonesInDeepFreeze
3.8krelying on the assumption that said pattern repeats indefinitely by virtue of being a pattern. — Benj96
Proof that certain reals have infinite expansions does not rely on assumptions that patterns repeat.
so the only other way to determine it in the absolute is the exhaustive method - which is an endless endeavour in said case. — Benj96
No, it is not endless. Proofs in mathematics are what you call "exhaustive" in finite length. -
 TonesInDeepFreeze
3.8kI took out what I previously posted in this message. My questions were not needed.
TonesInDeepFreeze
3.8kI took out what I previously posted in this message. My questions were not needed. -
 jgill
4kIt's natural that on a philosophy forum discussions of mathematics will mostly lie within the intersection of philosophy and math. I've mentioned in the past that most mathematicians are not heavily involved with foundations, a speculation on my part stemming from my career. It's really hard to pin down exact figures but from the AMS site it would seem that very few degrees from math departments are in foundations, set theory, logic, etc. The 2017-18 stats show that, of 1,960 PhDs, 7% were in a grouping of discrete math, combinatorics, logic, and CS. So that perhaps 3% might have been in foundations, a guess.
jgill
4kIt's natural that on a philosophy forum discussions of mathematics will mostly lie within the intersection of philosophy and math. I've mentioned in the past that most mathematicians are not heavily involved with foundations, a speculation on my part stemming from my career. It's really hard to pin down exact figures but from the AMS site it would seem that very few degrees from math departments are in foundations, set theory, logic, etc. The 2017-18 stats show that, of 1,960 PhDs, 7% were in a grouping of discrete math, combinatorics, logic, and CS. So that perhaps 3% might have been in foundations, a guess.
Philosophy departments sometimes grant degrees in the philosophy of mathematics, and I don't have any figures there, beyond the figure of 477 total PhDs in philosophy in 2018. Also, CS departments might get deeply into foundations of math. Another glimpse into stats is papers submitted to ArXiv.org, and looking at May it would appear about 2.13% of papers in math were in logic or foundations, out of 1,505 papers submitted. My area(s) - Complex Variables and Dynamic Systems - account for about 8%.
I looked this info up out of curiosity. You may or may not find it of interest. :cool: -
 TonesInDeepFreeze
3.8kI'd be curious what the percentages are for each of the branches. To not have it too Balkanized, it would have to be large groupings like:
TonesInDeepFreeze
3.8kI'd be curious what the percentages are for each of the branches. To not have it too Balkanized, it would have to be large groupings like:
Foundations, Algebra, Analysis, Topology, Geometry, Number Theory, Combinatorics. Graph Theory, Probability and Statistics, Applied, Game Theory -
 jgill
4kAnalysis at arXiv runs about 25% of the papers in math in May. Foundations 2.13%. Surprisingly, topology runs only 3%. Algebra and its offshoots looks like it dominates.
jgill
4kAnalysis at arXiv runs about 25% of the papers in math in May. Foundations 2.13%. Surprisingly, topology runs only 3%. Algebra and its offshoots looks like it dominates.
The American Philosophical Society doesn't seem to separate PhD areas, so its hard to estimate how many are in math. -
 TonesInDeepFreeze
3.8kInteresting that Algebra dominates. I would have thought it would be Analysis and its offshoots.
TonesInDeepFreeze
3.8kInteresting that Algebra dominates. I would have thought it would be Analysis and its offshoots. -
 jgill
4kSince I last checked 137 math papers have been uploaded to ArXiv. The rate of research in math is staggering, as are the number of specialized topics. It looks like algebra and its offshoots account for about 26% of the total. Only 2% in complex variable theory, my general area, outdone by logic/set theory/p-s topology/formal math - one category - which comes in at 2.13%. How much of that is foundations is difficult to ascertain. Even in CV theory its hard for me to understand many of the titles.
jgill
4kSince I last checked 137 math papers have been uploaded to ArXiv. The rate of research in math is staggering, as are the number of specialized topics. It looks like algebra and its offshoots account for about 26% of the total. Only 2% in complex variable theory, my general area, outdone by logic/set theory/p-s topology/formal math - one category - which comes in at 2.13%. How much of that is foundations is difficult to ascertain. Even in CV theory its hard for me to understand many of the titles.
I hope taxpayers are not footing the bill for most of this activity - much of it just intellectual exercises useful for academic promotion, prestige, etc. I've been on grants before and even at the time felt it was not a productive use of public monies. :brow: -
 ssu
9.8k
ssu
9.8k
Algebra I think is a larger branch of Math or comes first.Interesting that Algebra dominates. I would have thought it would be Analysis and its offshoots. — TonesInDeepFreeze
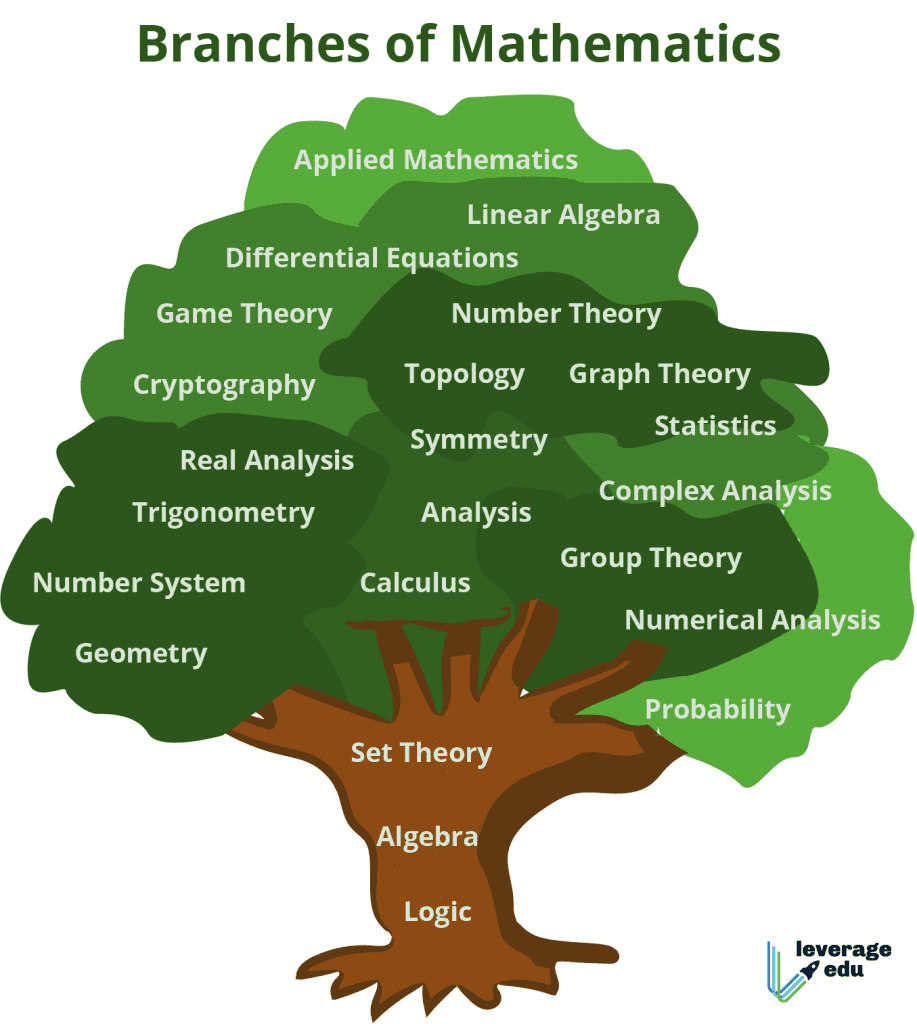
-
 TonesInDeepFreeze
3.8kAsI've been on grants before and even at the time felt it was not a productive use of public monies. — jgill
TonesInDeepFreeze
3.8kAsI've been on grants before and even at the time felt it was not a productive use of public monies. — jgill
As a taxpayer, I'm quite happy for my share - my .00002 cents - to have contributed to your research. More, if I had it to give. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
I don't like that tree. The order and proximities seem incorrect and haphazard in places.The Venn diagram is better. -
 jgill
4k
jgill
4k -
TheMadFool
13.8kTherefore, is it impossible to create a perfect circle?
A circle made with 3.14159 is better than one made with 3.1 — Benj96
We don't draw circles using pi, we fix a point as the center, choose a radius and use a compass to draw a circle. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
For me, mathematical logic and set theory are chicken and egg. To formalize set theory, we use the first order predicate calculus, which is a subject of mathematical logic. But to formalize mathematical logic, we use set theory. So I don't think we should put one below the other in a tree.
(And I don't know why Algebra is placed between them on that tree. Granted, propositional logic can be described as a Boolean algebra, and first order logic as a cylindric algebra, but those results themselves can be described set theoretically.) -
 RogueAI
3.5kI have a low understanding of this. It seems to me that a number like 2 is just a label for the idea of "a thing and a thing", and that 1+1 has to equal 2 because if you have a thing + a thing, necessarily, you have thing and thing (2). What am I missing?
RogueAI
3.5kI have a low understanding of this. It seems to me that a number like 2 is just a label for the idea of "a thing and a thing", and that 1+1 has to equal 2 because if you have a thing + a thing, necessarily, you have thing and thing (2). What am I missing? -
 jgill
4kI just came across this quote from Mathematics Made Difficult by Linderholm. It points to the spirit of modern set theory and foundations :cool: :
jgill
4kI just came across this quote from Mathematics Made Difficult by Linderholm. It points to the spirit of modern set theory and foundations :cool: :
“The days when one could get up from the dinner-table and leave the room at the mention of the Axiom of Choice are gone with the wind, and we must accustom ourselves to the new ways, the ways of tomorrow.”
And I don't know why Algebra is placed between them on that tree — TonesInDeepFreeze
An algebraist drew the tree? -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum






