-
 SkyLeach
69Your perspective of "set theory" is not the normal math perspective. If it works for you, fine — jgill
SkyLeach
69Your perspective of "set theory" is not the normal math perspective. If it works for you, fine — jgill
The point was that I have both perspectives. I double majored in mathematics. This being a philsophy forum I default to the more general view (and certainly in this context discussing the mathematics-only perspective would make little sense).
I'm also curious why you just skipped over the whole part about a vecor being defined by element association since that was the mathematics perspective and the practical application perspective. -
 SkyLeach
69As far as I can tell he's just using the singular form of a word and saying it can't be counted which is kinda like saying "can the number 1 be counted".
SkyLeach
69As far as I can tell he's just using the singular form of a word and saying it can't be counted which is kinda like saying "can the number 1 be counted".
The answer is, of course, yes that's the definition of commutative principle we just use a different word with a root modifier for plurality instead of the singular.
That's why I said it didn't make any sense. You can have multiple surfaces, consciousnesses, etc... -
 jgill
4kI'm also curious why you just skipped over the whole part about a vecor being defined by element association since that was the mathematics perspective and the practical application perspective. — SkyLeach
jgill
4kI'm also curious why you just skipped over the whole part about a vecor being defined by element association since that was the mathematics perspective and the practical application perspective. — SkyLeach
These are vectors as I know them. I guess I don't understand what exactly you are talking about. That could be me. But if you point out your description in the article that would be good. -
 SkyLeach
69
SkyLeach
69
Yes, it's literally the first sentence.In mathematics and physics, a vector is an element of a vector space.
Trouble is, then we have to get into what a vector space is...
In mathematics, physics, and engineering, a vector space (also called a linear space) is a set of objects called vectors, which may be added together and multiplied ("scaled") by numbers called scalars. Scalars are often real numbers, but some vector spaces have scalar multiplication by complex numbers or, generally, by a scalar from any mathematic field.
And from there we have to get into specific allegorical definitions (while trying to avoid jargon) in order to limit the definition of 'element association'.
Really though, at this point the specifics are specious since the bolded part of the definition of vector space pretty much covers it.
My word "association" is indistinguishable from the definition of mathematic field:
In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers do.
Maybe a real-life example would clear it up better though
In radiology the system that stores images is called PACS. Most of the time, those systems deal with DICOM images. Those images can be regular computer graphics, but not for things like PET. PET is stored as a matrix defined in the sagittal, axial and transaxial planes. The value of each element in the matrix is called a Housfield scalar. It's a relative absorbtion rate (defined by the precision of the PET hardware) between 0-255 (or bigger).
You can't do anything with the matrix in that form, however. You must either convert it to a 2D vector space or a 3D vector space. You can do this directly or by scaling it in a process called fusion with MRI or CT data which is generally stored as a more traditional JPEG2k or MPEG.
Thus, the resulting vector space is either a 3 element vector of (x,y,h) or 4 element vector of (x,y,z,h) with x,y and z mapped to the coordinate space and h mapped to the housfield absorbtion.
It's a whole other dimension, but it's still valid. -
 SkyLeach
69Yeah I worded that poorly. I was thinking ray as applied to a function but talking about vectors.
SkyLeach
69Yeah I worded that poorly. I was thinking ray as applied to a function but talking about vectors.
Anyhow, here:
{(5, 2, 4, 0, 0.0), (5, 2, 4, 1, 0.8414709848078965), (5, 2, 4, 2, 0.9092974268256817), (5, 2, 4, 3, 0.1411200080598672), (5, 2, 4, 4, -0.7568024953079282), (5, 2, 4, 5, -0.9589242746631385), (5, 2, 4, 6, -0.27941549819892586), (5, 2, 4, 7, 0.6569865987187891), (5, 2, 4, 8, 0.9893582466233818), (5, 2, 4, 9, 0.4121184852417566), (5, 2, 4, 10, -0.5440211108893698), (5, 2, 4, 11, -0.9999902065507035), (5, 2, 4, 12, -0.5365729180004349), (5, 2, 4, 13, 0.4201670368266409), (5, 2, 4, 14, 0.9906073556948704), (5, 2, 4, 15, 0.6502878401571168), (5, 2, 4, 16, -0.2879033166650653), (5, 2, 4, 17, -0.9613974918795568), (5, 2, 4, 18, -0.7509872467716762), (5, 2, 4, 19, 0.14987720966295234)}
Edit the ray stops at 20, but that was to keep the post short.
Edit2: it should be pointed out that since you didn't define the association, the possibilities are infinite. The only way to make it useful is to define how they're associated. -
 Agent Smith
9.5kAre you arguing this way?:
Agent Smith
9.5kAre you arguing this way?:
The set of real numbers can't be counted.
Consciousness can't be counted.
Consciousness is not mathematical.
Therefore, the set of real numbers is not mathematical. — TonesInDeepFreeze
More or less. I'm sucker for (good) analogies. -
 TonesInDeepFreeze
3.8kAFAIK one doesn't use braces for subsets — SkyLeach
TonesInDeepFreeze
3.8kAFAIK one doesn't use braces for subsets — SkyLeach
This distinction between, on the one hand, a set in and of itself without specifying an order and, on the other hand, an ordered tuple is crucially basic to mathematics, especially linear algebra.
Curly braces are used for sets in general. Either by set abstraction such as
{x | x is a natural number less than 4}
or for specifying the members individually such as
{0 1 2 3 }
where the order in which the members are listed, or redundancies are irrelevant, so:
{0 1 2 3} = {3 1 0 2} = {3 3 1 0 2} etc.
Angle brackets [alternatively, parenthesis] are used for order tuples such as
<0 1 2 3 > [alternatively (0 1 2 3)]
and order and redundancy do matter, so none of the below are equal to one another:
<0 1 2 3>
<3 1 0 2>
<3 3 1 0 2>
etc.
/
This is not just a matter of notation, but is a crucial concept, especially in linear algebra. I don't know why someone would be posting such bold claims as yours about mathematics and linear algebra while not even knowing that there is a distinction between merely a set and an ordered tuple.
Saying that linear algebra is the foundation of mathematics while not knowing the basic notion of an ordered tuple is like saying benzene rings are the foundation of chemistry while not knowing what an atom is. -
 SkyLeach
69This is not just a matter of notation, but is a crucial concept, especially in linear algebra — TonesInDeepFreeze
SkyLeach
69This is not just a matter of notation, but is a crucial concept, especially in linear algebra — TonesInDeepFreeze
Of course it is, but I am not a mathematician and you're literally talking about writing style. I pointed that out already. You're talking about notation which is literally how you write it down by definition so that there isn't a bunch of words needed to explain things.
I literally said exactly that:
AFAIK one doesn't use braces for subsets but then since I'm not a mathematician by trade I don't really know anything about how mathematicians do things — SkyLeach
See, in the real world people can't specialize in everything. There are limits to how much jargon and special notation and career details a generalist can cover because there just isn't any possible way to read and remember every possible detail of every discipline, even if you spent 100% of your time doing nothing but learning and no time at all in practical application.
And you're just plain wrong about it not being "just a matter of notation". That's bloody well exactly what it is and it's specialized for your particular field because it makes sense in a field where you write down equations all the time. In fields where writing equations is a complete waste of time except for the rare instance when it's going into the documentation it's mostly worthless trivia.
As for knowing it there would be absolutely no difference at all in me saying you don't know linear algebra because you didn't know that what I pasted into my post was set notation for a set of tuples (immutable ordered sets).
If I had thought you'd try such a specious and obvious Ad Hominem attack merely because you don't like my argumet I would have taken the time to run the output through SymPy. I'd have done that because it's a tool for turning functional code notation into symbolic mathematics notation.
The tool's purpose is to ease the grunt work required to turn functional logic into symbolic mathematics for publication because ain't nobody got time for that shit but a mathematician.
I don't know why someone would be posting such bold claims as yours about mathematics and linear algebra while not even knowing that there is a distinction between merely a set and an ordered tuple.
Saying that linear algebra is the foundation of mathematics while not knowing the basic notion of an ordered tuple is like saying benzene rings are the foundation of chemistry while not knowing what an atom is. — TonesInDeepFreeze
Blah blah blah "HAHA! I found you out! Have at the pretender!"
Seriously what the hell is your problem? I don't care if you like the argument for set theory based axioms or not. It's a core concept of the philosophy of mathematics and I think it makes a lot of sense but I'm not on a crusade to make you accept it and you had no call whatever to try to trick me so you could try to shame me.
It doesn't really matter that you failed completely (and made yourself look like a jackass) so much as the fact that I'm a real person. I have real feelings. I like people and genuinely enjoy talking about philosophy and so far all I've gotten since I came here is a bunch of angry people trying to take out their personal issues on random strangers.
Seriously, go see a professional and deal with your issues, not my fault and I don't deserve your shit.
EDIT: I also didn't now that Python borrowed the term "Tuple" from mathematics. Cool. I learned a new etymology. So yeah, I guess I could have answered your question easily if I had known we shared that. -
 TonesInDeepFreeze
3.8kangry people — SkyLeach
TonesInDeepFreeze
3.8kangry people — SkyLeach
I'm not angry about you.
you're literally talking about writing style — SkyLeach
No, that's the point, I'm not. I'm talking about the very concept, as it was mentioned to you by even another poster. Moreover, even if it were merely (which it is not) notation, then still it is hard to imagine anyone has studied linear algebra without having seen this utterly ubiquitous notation.
Anyway, now that I've given you an explicit explanation, you may understand the difference between a set taken in and of itself and an ordered tuple, and you now have the common notation you may use going forward to contribute to communicating clearly about mathematics with people who have actually studied it and know about linear algebra.. -
 SkyLeach
69That's not how language and the brain work. It's got nothing whatever to do with what I said about sets.
SkyLeach
69That's not how language and the brain work. It's got nothing whatever to do with what I said about sets.
I just feel sad that yet again my hopes of having a good conversation has met a disaster of self loathing instead of a peer. -
 SkyLeach
69It's not a joke, he's saying that your semantic mess is ridiculous.
SkyLeach
69It's not a joke, he's saying that your semantic mess is ridiculous.
As much as I can't stand that guy, he's right. Your entire argument is semantic and rooted in an incomplete understanding of the philosophy of mathematics and semantic meaning of the words you are using. -
 Agent Smith
9.5kIt's not a joke, he's saying that your semantic mess is ridiculous. — SkyLeach
Agent Smith
9.5kIt's not a joke, he's saying that your semantic mess is ridiculous. — SkyLeach
Pray tell, how is what I wrote/said ridiculous? :smile:
I want to run something by you since you seem to know your way around the philosophy of math.
I recall a video im which Michio Kaku says (paraphrasing) "In blackholes, the (relevant) equations when used result in this: and then physicists can't make head or tail of it. Math breaks down"
If does that to math, is mathematical? -
 SkyLeach
69Some MK quotes...
SkyLeach
69Some MK quotes...
Once again, my colleague Stephen Hawking has upset the apple cart. The event horizon surrounding a black hole was once though to be an imaginary sphere. But recent theories indicate that it may actually be physical, maybe even a sphere of fire. But I don't trust any of these calculations until we have a full-blown string theory calculation, since Einstein's theory by itself is incomplete. — Michio Kaku
Combining quantum entanglement with wormholes yields mind boggling results about black holes. But I don't trust them until we have a theory of everything which can combine quantum effects with general relativity. i.e. we need to have a full blown string theory resolve this sticky question. — Michio Kaku
If I completely avoid theoretical physics questions and stick to mathematics do you notice something here?
I'm specifically talking about MK's approach to theories not his own...
Mathematics is a declarative language. You can make statements. You can make incomplete statements if you provide variables or equations with variables. You cannot, however, speculate or expound on theory. Mathematics is also linear. It makes clearly defined logical statements in a linear series. You can make a linear set of those linear statements. You can stack up as many linear statements describing as many dimensions or universes as you like too.
MK is a theoretical physicist specializing in cosmology and grand unified theory.
The problem MK (and all other theoretical physicists) are running into with their theories is the difficulty of constructing an analogy of sufficiently granular specificity (enough details/variables) to describe the function of the universe linearly and in an unbroken form from quantum theory into relativity (Einstein space-time).
Add to that MK's problem accepting any theory not his own and he says some truly whacked out things on a regular basis. I couldn't find your quote, but just from the ones I did find we already know he's going to utterly disagree with QMRE (quantum-modified Rocharch Equation) and infinite universe because any times infinite anything comes up (or the math showing that super-blackholes just can't form - based on Radjaharma's sp? research) he just says "bullshit" and ignores it.
He doesn't debate. He doesn't offer explanations. He doesn't refute. He just says it's not worth his valuable time. It's 100% ego-driven logic.
If ∞ does that to math, is ∞ mathematical? — Agent Smith
Nope. It doesn't do that. That's a linear assumption, NOT an axiom. It's not a proof. It isn't part of mathematics at all. It's just a belief held by some people with big egos and funding to defend. -
 Agent Smith
9.5kIf ∞ does that to math, is ∞ mathematical?
Agent Smith
9.5kIf ∞ does that to math, is ∞ mathematical?
— Agent Smith
Nope. It doesn't do that. That's a linear assumption, NOT an axiom. It's not a proof. It isn't part of mathematics at all. It's just a belief held by some people with big egos and funding to defend. — SkyLeach
Can we do math with ? Try some basic operations (+ × ÷ -) on it and check what happens. -
 SkyLeach
69Yes of course. It's just like any other variable symbol.
SkyLeach
69Yes of course. It's just like any other variable symbol.
(I tried bbcode math and mathml and texzilla but this forum doesn't support it :-( )
No work
UTF-8 but no solve 'cause not MathML\sqrt(\infinity*\infinity)=\infinity*1
The Fourier Transform (signals math) - edit: this looks horrid. (appended what it should look like)∞+1= ∞+1-1= ∞*1
f(x)=∑n=−∞∞cne2πi(n/T)x=∑n=−∞∞f^(ξn)e2πiξnxΔξ
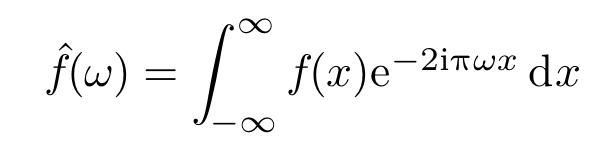
edit: and here is what it's doing:

You see what I mean now? You can't sum up infinity so you can't solve the answer to ∞*2 but you can work with it like any other variable and to do many modern forms of equation you have to.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum




