-
creativesoul
12.2k
I'm not sure if it's an equivocation of "true" or a way to show that both correspondence and coherence are exhausted. The latter would be very unique. -
 Banno
30.2k
Banno
30.2k
I had a read an ignored that, since I couldn't make sense of "sense" there - it's truth-functional Boolean algebra all the way down.Not true in the same sense that any of the left side utterances are though. — creativesoul
Now you have Meta agreeing with you. A sure sign of a problem. -
 Banno
30.2kBetter. Neither correspondence nor coherence are at work here. It's a formal language with truth defined in terms of satisfaction.
Banno
30.2kBetter. Neither correspondence nor coherence are at work here. It's a formal language with truth defined in terms of satisfaction.
An object o satisfies a predicate f if and only if ((f="is english" and o is English) or (f="is french" and o is french)
We have
For any sentence p, p is true if and only if ϕ
and given designation and satisfaction, we can take any sentence p in the object language and develop a sentence in the metalanguage that both designates the same things and is satisfied in the same conditions. — Banno -
 Metaphysician Undercover
14.7k
Metaphysician Undercover
14.7k
The problem with your approach is that logic is the means for justification. So when you define truth in terms of satisfaction you simply reduce "true" to justified in a special way. Some of us like to maintain a separation between true and justified, such that they are distinct properties. Therefore we can see that defining truth in this way is simply a way of avoiding what it really means to be true. So you propose a purposeless exercise. -
 Banno
30.2k
Banno
30.2k
See the truth table for ≡
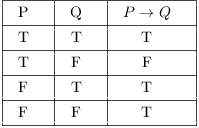
and, p≡q is by definition (p⊃q)&(q⊃p)
hence
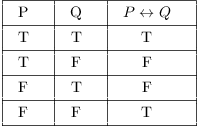
Notice the last line. The equivalence is true when the terms on either side have the same truth value, false otherwise.For every possible statement "S" in an object language, an S may be found in a metalanguage. — RussellA
To be sure, "S" is constructed using designation and satisfaction.
An analogue would be finding the person designated by "Jean" in French and designating them "John" in English, and taking the predicate "...est anglais" and finding it refers to the very same individuals as the English phrase "...is English", and writing
"Jean est anglais" is true IFF John is English
This is how Tarski avoids the problem to which drew attention, which i summarised here:
Bowdlerising the argument, suppose we call "Snow is white", Fred.
Then we can write
Fred is true IFF snow is white
And perform a universal generalisation to get
U(x) Fred is true IFF x
...which is not what we want. — Banno
S is not just any sentence, it's the one that has the same meaning as "S". -
 Banno
30.2khe problem with your approach is that logic is the means for justification. — Metaphysician Undercover
Banno
30.2khe problem with your approach is that logic is the means for justification. — Metaphysician Undercover
Yes, I understand that using logic as a justification is a problem for you. -
 Banno
30.2kThe Revision Theory
Banno
30.2kThe Revision Theory
So we looked at Tarski and at Kripke's theories fo truth. Tarski seems to be the theory in which folk are most interested, from the replies. I suppose Kripke's use of a trinary logic is daunting.
Each of those theories has as a central problem, the liar paradox:
This sentence is false
The liar is perhaps the simplest case of a series of sentences that cause all sorts of grief.
Consider the Knights and knaves problem:
The solution is found by assigning different truth values to the guardian's statements, and working out the consequences.
"Would the other guard tell me that your door leads to the castle?"
We consider the potential case.
Here's the first option: Guard one says the other knight would say "yes"
if guard one is a knight, then guard two is a knave, and "yes' is a lie, so guard one's door does not lead to the castle.
If Guard one is a knave, then Guard two is a knight, and "Yes" is a lie, so again guard one's door does not lead to the castle.
In either case Guard two's door leads to the castle.
Here's the second option, a revision of the first: Guard one says "no"
If guard one is a knight, then guard two is a knave, and "no" is the a lie, so guard one's door leads to the castle.
If guard one is a knave, then guard two is a knight, and "no" is a lie, so guard one's door leads to the castle.
So which ever guard one asks, if they answer "yes" their door does not lead to the castle, and if they answer "no" is does.
With this question, the knight will tell the truth about a lie, while the knave will tell a lie about the truth. Therefore, the given answer will always be the opposite of the correct answer to the question of whether the door leads to the castle.
The problem was described by considering one potential response, then revising that response. In this case, the solution is closed, and an answer is found.
Now lets' follow the same process for the Liar.
First we suppose that "this sentence is false" is true. We deduce that the sentence is therefore false.
Given this result, we revise our supposition, supposing instead that "this sentence is false" is false. We deduce that therefore the sentence is true.
And so on. Unlike the Knights and Knaves example, the answer flip flops between true and false.
It seems the revision theory does not seek to resolve the liar paradox, but instead to classify it as one outcome amongst a range of outcomes, closed or open or undecided, and hence to develop a theoretical basis for the examination of such sentences. It is somewhat sympathetic to the prosentential version of deflation, treating truth as a function rather than as a property.
Doubtless this is not a very clear exposition, but it's newish stuff. it's included here as indicating a different direction for the logical of truth. -
 Metaphysician Undercover
14.7kYes, I understand that using logic as a justification is a problem for you. — Banno
Metaphysician Undercover
14.7kYes, I understand that using logic as a justification is a problem for you. — Banno
Obviously you don't understand. It appears you didn't read the post, yet claimed to understand me. That's a mistake. You ought to read the post, or not bother to make a reply, which is what you usually do.
Using logic is the means for justification, as I said. No problem. The problem is with your approach to truth, as I also said. Truth is not a special case of being justified, as you seem to think. Do you have a coherent reply to this, or will you stick to your usual? -
 Banno
30.2kCheers, Meta. No, I don't claim to understand you. I don't think you do logic.
Banno
30.2kCheers, Meta. No, I don't claim to understand you. I don't think you do logic.
It's not my approach. It's formal logic over the last hundred and fifty years. You are behaving here in much the same eccentric way as when you discuss . -
 Metaphysician Undercover
14.7kIt's not my approach. It's formal logic over the last hundred and fifty years. — Banno
Metaphysician Undercover
14.7kIt's not my approach. It's formal logic over the last hundred and fifty years. — Banno
When you accept, adopt, and preach that approach, then it is yours. All of us here are rational human beings with the capacity to think for ourselves, and freely make our own decisions. That it is the approach of formal logic over the last hundred and fifty years, to portray "true" as a special form of justified, is no reason to accept this approach yourself. That's a fallacy known as appeal to authority. -
 Banno
30.2kYeah. A few posts back you confused = with ≡.
Banno
30.2kYeah. A few posts back you confused = with ≡.
So forgive me if I don't follow through on your comments. -
 Banno
30.2kA few posts back you confused = with ≡. — BannoSorry, you must be talking about someone else. — Metaphysician Undercover
Banno
30.2kA few posts back you confused = with ≡. — BannoSorry, you must be talking about someone else. — Metaphysician Undercover
If "p" is true IFF p, and "p" is true IFF q, then p and q are the very same thing. I agree that this is very trivial, but it says absolutely nothing useful about the relation between meaning and truth. That is because you've exclude meaning from truth, by reducing truth to a statement of identity, saying that "q" and "p" must signify the very same thing. — Metaphysician Undercover
So there's that. Cheers. -
 Metaphysician Undercover
14.7k
Metaphysician Undercover
14.7k
So, where's this use of = and ≡ you are talking about? I only see "Iff" here, which I clearly did not confuse with "=", nor did I confuse it with "≡". In case you are unfamiliar with language, different symbols have different uses, and also different meanings. Please do not misquote me anymore. -
 Metaphysician Undercover
14.7k
Metaphysician Undercover
14.7k
Again, it would be beneficial to the conversation if you would actually read what a person writes. -
 Banno
30.2kIf "p" is true IFF p, and "p" is true IFF q, then p and q are the very same thing. — Metaphysician Undercover
Banno
30.2kIf "p" is true IFF p, and "p" is true IFF q, then p and q are the very same thing. — Metaphysician Undercover
So you can't even see where this is wrong. -
 Metaphysician Undercover
14.7k
Metaphysician Undercover
14.7k
Now we're getting somewhere. Perhaps you might explain why you see it as wrong. -
 Metaphysician Undercover
14.7kHere's an off topic question for you Banno. If you don't like it, complain to the mods. Why did you start a new thread on "truth", distinct from the old one, then import a post of mine from the other thread, to discuss it here, instead of over there?
Metaphysician Undercover
14.7kHere's an off topic question for you Banno. If you don't like it, complain to the mods. Why did you start a new thread on "truth", distinct from the old one, then import a post of mine from the other thread, to discuss it here, instead of over there? -
 Metaphysician Undercover
14.7k
Metaphysician Undercover
14.7k
So you imported that post for no reason? You have no desire to discuss it? -
 Metaphysician Undercover
14.7k↪Metaphysician Undercover
Metaphysician Undercover
14.7k↪Metaphysician Undercover
If "p" is true IFF p, and "p" is true IFF q, then p and q are the very same thing.
— Metaphysician Undercover
So you can't even see where this is wrong. — Banno
Look Banno, the judgement that "p" is true requires the fulfillment of a very special and unique set of circumstances, a particular set of circumstances. Saying "p" is true IFF p, is to say that there is a unique and special relation between "p" and p. If you also say "p" is true IFF q, then you say that both p and q have the very same unique and special relation with "p". Therefore both p and q must refer to the very same particular set of circumstances. Both p and q must refer to the very same thing. -
 Michael
16.6kMaybe use an actual example.
Michael
16.6kMaybe use an actual example.
“John is a bachelor” is true iff John is a bachelor
“John is a bachelor” is true iff John is an unmarried man
This shows us the meaning of “bachelor”. -
 Metaphysician Undercover
14.7k
Metaphysician Undercover
14.7k
So "a bachelor" is p, and "an unmarried man" is q. You can see that p and q refer to the very same thing. -
 Metaphysician Undercover
14.7k
Metaphysician Undercover
14.7k
If you make any changes to what p refers to (a bachelor), or to what q refers to (an unmarried man), such that they no longer both refer to the very same thing, you can no longer make the same "is true iff" statements. Therefore p and q necessarily refer to the very same thing.
This shows us the meaning of “bachelor”. — Michael
No it does not, that's the point I made in the other thread. It just shows that "bachelor" and "unmarried man" refer to the very same thing, but it shows nothing about the meaning of those terms. For that, we'd have to look at the meaning of "unmarried", and of "man". The attempt to avoid the infinite regress of definitions is an illusion, and really a farce because it's so obviously simple sophistry. -
 RussellA
2.5kTarski seems to be the theory in which folk are most interested — Banno
RussellA
2.5kTarski seems to be the theory in which folk are most interested — Banno
"Small moves, Banno, small moves"
This is how Tarski avoids the problem to which @Michael drew attention — Banno
My understanding is correct IFF my understanding is correct.
My instinctive belief is as @Michael wrote ""'p' is true iff p" isn't the definition of truth but something which follows from whatever the actual definition is". This leads into @Banno's quote that "Neither correspondence nor coherence are at work here. It's a formal language with truth defined in terms of satisfaction."
Consider "schnee ist weiss" is true IFF snow is white
What is "designation"
I perceive the word "snow" and designate it "schnee", such that "schnee" mean "snow". I perceive the word "white" and designate it "weiss", such that "weiss" means "white".
What is the mechanism of "satisfaction"
From the IEP: "The Semantic Theory of Truth"
Consider the open formula "x is a city", open because it has a free variable.
The formula is satisfied by London, so "London is a city" is true
The formula is not satisfied by The Thames, so "the Thames is a city" is false
Satisfaction turns an open formula into a true sentence, and non-satisfaction turns an open formula into a false sentence
Based on @Banno, an object o satisfies a predicate f IFF either the object o is snow and the predicate f is "is snow" or the object o is schnee and the predicate f is "ist weiss".
What is intensional and extensional
The quote marks around "snow is white" makes it intensional. Intensional means analytic, reasoning from abstract rules, what Quine calls "meaning" and what is necessary to make a concept.
P ↔ Q means biconditional, it means P IFF Q, it also means P implies Q and Q implies P. The meanings of P and Q are extensional. Extensional means synthetic, involves examples from the world, what Quine calls "reference" and what is contingent to a concept.
Replacing the T-Schema "schnee ist weiss" is true IFF snow is white by the equivalent T-Schema "snow is white" is true IFF snow is white
@Banno wrote: "Tarski gets past this for formal languages by developing the mechanism of satisfaction, so that he has extensionally transparent terms on both sides of the equivalence". This means that the extensional meaning of "schnee ist weiss" is the same as the extensional meaning of snow is white, because of the mechanism of satisfaction.
Because "schnee" has been designated as "snow", and as ""weiss" has been designated as "white", the intensional meaning of "schnee is weiss" is the same as the intensional meaning of "snow is white".
Therefore we can replace the T-Schema "schnee ist weiss" is true IFF snow is white by the equivalent T-Schema "snow is white" is true IFF snow is white.
Introducing extensional meaning
Tarski is saying that the extensional meaning of "snow is white" is equivalent to the extensional meaning of snow is white.
In this case, the T-Schema may be written as: the extensional meaning of "snow is white" is true IFF it is equivalent to the extensional meaning of snow is white.
The problem with the extensional meaning
The problem is, why should the extensional meaning of "snow is white" be equivalent to the extensional meaning of snow is white?
The T-Schema has become tautological. It may be written in full as: the extensional meaning of "snow is white" is true IFF it is equivalent to the extensional meaning of snow is white given that the extensional meaning of "snow is white" is equivalent to the extensional meaning of snow.
The core problem with the T-Schema as a definition of truth without circularity is that it is founded on a conditional, the conditional IFF, which is saying no more than x is true IFF x is true. The T-Schema is a tautology, it is analytic.
The truth tables reinforce the conditionality of the T-Schema
The truth table for material conditional uses the conditional, and the truth table for material biconditional uses the conditional.
A valid definition of truth cannot be founded on a conditional
A definition of truth cannot be founded on a conditional, as this leads to a tautology. A valid definition of truth must avoid the conditional. For example, i) "truth is what I say it is" is a valid definition of truth, ii) the performative act "I name this ship Queen Elizabeth" means that it is true that this ship is named Queen Elizabeth and iii) I perceive something in the world and name it "snow" means that it is true that "snow" is snow.
As an aside, my perception of something in the world that is cold, white and frozen and name it "snow" means that there is a correspondence between "snow" and snow. However such correspondence is not purely cognitive, but is founded on something visceral, thereby avoiding the problem of belief as a truth bearer.
Summary
The T-Schema is based on the conditional IFF, which is fixed by the mechanism of satisfaction. Yet the mechanism of satisfaction is itself based on another conditional, again leading to circularity.
It seems to me that a valid definition of truth cannot rely on a conditional, which Tarski's Semantic Theory of Truth does. -
 Banno
30.2kI perceive the word "snow" and designate it "schnee", such that "schnee" mean "snow". I perceive the word "white" and designate it "weiss", such that "weiss" means "white". — RussellA
Banno
30.2kI perceive the word "snow" and designate it "schnee", such that "schnee" mean "snow". I perceive the word "white" and designate it "weiss", such that "weiss" means "white". — RussellA
Better, Tarski looks to those things to which "Schnee" points in the object langauge and chooses new words in the metalangauge to point to the same things. SO "Snow" has the same extension as "Schnee" -
 Agent Smith
9.5kThe OP is quite clear; if you pick a definition, any definition, of truth, you'll have to explain yourself.
Agent Smith
9.5kThe OP is quite clear; if you pick a definition, any definition, of truth, you'll have to explain yourself. -
 javi2541997
7.1k
javi2541997
7.1k
It is not clear at all because the language used in logic is very complex. I can explain it to myself but how can I know that I am not wrong? This is why I don't tend to take part in threads about logic. The Language used likep≡q is by definition (p⊃q)&(q⊃p)
Is difficult to follow and understand if you do not have basic skills inside logic.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum





