-
 plaque flag
2.7kThe symbolism seems to me entirely irrelevant. The idea 2+2=4 can be represented in Roman numerals, binary notation, the Babylonian number system, etc. — Art48
plaque flag
2.7kThe symbolism seems to me entirely irrelevant. The idea 2+2=4 can be represented in Roman numerals, binary notation, the Babylonian number system, etc. — Art48
The body is arbitrary but a body is necessary. The dove found that it could fly faster in thinner air and was confident it would fly still faster in a vacuum.
This is why, by the way, the body or vessel metaphor is potentially misleading. An equivalence class is a less mystified approach -- unless Mystification is the Point. -
 plaque flag
2.7kSo, in my view, I directly experience sensations: i.e., the five physical senses, emotions, and thoughts. Everything else is an idea that makes sense of my perceptions.
plaque flag
2.7kSo, in my view, I directly experience sensations: i.e., the five physical senses, emotions, and thoughts. Everything else is an idea that makes sense of my perceptions.
Therefore, my sensations have a more secure epistemological status than a theoretical construct I create to explain my sensations. My ideas certainly have reality and existence. Matter, maybe, maybe not. — Art48
This is a classic view. It's the model-T of metaphysics. You should at least test drive something from the 20th century. :starstruck: -
 plaque flag
2.7k
plaque flag
2.7k
:up:it's a concession to both reductionism and reification to accept that only physical objects exist. — Jamal
It's also hard to make sense of the claim that only such objects exist, perhaps because that sense would not itself exist, unless as a physical object ? If senses (ideas) are physical object, what is not physical ? Where's the contrast that makes the claim more than a tautology ?
partly what motivated Markus Gabriel's ontology, in which tables, quarks, numbers, nations, and ideas all exist. — Jamal
Haven't read Gabriel, but I can relate. The world (lifeworld) is a swirling unity of relationships. We believe in quarks because we trust scientific norms which were invented by primates who evolved with the help of DNA which is explained by physics and we are back to quarks. -
 Wayfarer
26kIt's also hard to make sense of the claim that only such objects exist, — green flag
Wayfarer
26kIt's also hard to make sense of the claim that only such objects exist, — green flag
This argument came out of my attempt to show that ‘existence’ pertains to phenomenal objects, and that intelligible objects, like number, exist in a different way to phenomenal objects, in that they can only be grasped by rational thought, not by the senses. Russell uses the term ‘to subsist’ in distinction from ‘to exist’. They are, in the pre-Kantian sense, ‘noumenal’, meaning, ‘objects of nous’. (I say pre-Kantian because Kant appropriated the term ‘noumenal’ for another purpose.) I think that distinction can be mapped against hylomorphism, but that since the abandonment of scholastic realism concerning metaphysics, it is a distinction which has become lost in the modern lexicon. So I’m not saying that they’re non-existent, but that they’re real in a different sense to phenomenal objects.
(This is also related to the negative theology of Paul Tillich, for anyone familiar.) -
 plaque flag
2.7k
plaque flag
2.7k
I wouldn't even say they are so different. They are just more abstract. We grasp objects (artichokes and aardvarks) as unities, which makes them countable. If Cantor is right, there are two basic operations of abstraction in this context, ordinal and cardinal. If you haven't read Cantor, this one is a gem:
https://www.amazon.com/Contributions-Founding-Transfinite-Numbers-Mathematics/dp/0486600459/
It's some beautiful, revolutionary math. So I recommend it to anyone who wants in on the infinity of infinities.
You might like:
https://www.amazon.com/Early-Heidegger-Medieval-PhilosophyPhenomenology/dp/0813221870/
A man of faith takes what he can from what he calls Heidegger's "phenomenology for the godforsaken." Lots of scholastic thought in it, as Heidegger started there, eventually incorporating Luther's thought as well as various mystics. The author even thinks that it's only after a kind of atheist moment that a genuine theology is possible. Something like that ! I'm reading it off and on with a pile of other books. -
 Wayfarer
26kI wouldn't even say they are so different. — green flag
Wayfarer
26kI wouldn't even say they are so different. — green flag
There is a difference between phenomenal objects which are temporally delimited and composed of parts, and those objects of thought which are not. Which is a distinction that I think is basic theme of Greek philosophy, between sensible and rational. Doesn't mean a dichotomy or a conflict, but a distinction. -
 plaque flag
2.7kThere is a difference between phenomenal objects which are temporally delimited and composed of parts, and the objects of thought. — Wayfarer
plaque flag
2.7kThere is a difference between phenomenal objects which are temporally delimited and composed of parts, and the objects of thought. — Wayfarer
I agree that we can discursively break the world up and think about the category or concept of a dog as apart from any particular dog. We indeed have that sort of metacognition.
Real dogs come and go. Concepts also come and go, but far more slowly, for the most part. "Impersonal conceptual schemes" (Braver) are something like a shared set of concepts that dominate and limit and make possible the thinking of a mortal generation. This is a synchronic abstraction, for time and the mutation of our concepts waits for no man. -
 Jamal
11.6k
Jamal
11.6k
Ideas, meanings, and thoughts are just not very thingy, are they? The static ontology of medium-size dry goods doesn’t feel right. (Some would say that a static ontology doesn’t even work for them either, which I suppose is process metaphysics.)
But numbers are more thingy than thoughts, while at the same time being not or less mind-dependent, and not situated in space and time. So there’s a scale of thingyness and an independent scale of abstractness. -
 plaque flag
2.7kThe static ontology of medium-size dry goods doesn’t feel right. — Jamal
plaque flag
2.7kThe static ontology of medium-size dry goods doesn’t feel right. — Jamal
:up:
Some would say that s static ontology doesn’t even work for them either, which I suppose is process metaphysics. — Jamal
Or Kojeve. Or Hegel (as I make sense of him, the system is always tumbling.)
But numbers are more thingy than thoughts, while at the same time being not or less mind-dependent, and not situated in space and time. — Jamal
I think instead of saying math isn't in space and time we should say that math methodically ignores the actual, local spatial and temporal situation. For instance, a Turing machine is understood to have unlimited space (its tape) and unlimited time (it can take as many discrete steps as it needs or run on forever.) No such computer can exist physically. But it's a great reasoning tool, since it saves us from worrying about space and time (which are worried about in complexity theory.)
Another example. The results of group theory in abstract algebra apply to any group, so it's killing an uncountably infinite number of birds with one stone. -
 plaque flag
2.7kSo there’s a scale of thingyness and an independent scale of abstactness. — Jamal
plaque flag
2.7kSo there’s a scale of thingyness and an independent scale of abstactness. — Jamal
I like considering more than one dimension. Our human situation is rich. James' pluralism comes to mind. There are lots and lots of kinds of things, perhaps as many as we care to notice or declare. -
 Wayfarer
26kI agree that we can discursively break the world up and think about the category or concept of a dog as apart from any particular dog. We indeed have that sort of metacognition. — green flag
Wayfarer
26kI agree that we can discursively break the world up and think about the category or concept of a dog as apart from any particular dog. We indeed have that sort of metacognition. — green flag
Which is the basis of the Theory of Forms.
I actually tracked down the source of this intuition I had about the Greeks and the ontological status of number:
Neoplatonic mathematics is governed by a fundamental distiction which is indeed inherent in Greek science in general, but is here most strongly formulated. According to this distinction, one branch of mathematics participates in the contemplation of that which is in no way subject to change, or to becoming and passing away. This branch contemplates that which is always such as it is and which alone is capable of being known: for that which is known in the act of knowing, being a communicable and teachable possession, must be something that is once and for all fixed. — Jacob Klein, Greek Mathematical Thought and the Origin of Algebra.
When I experienced the 'aha' moment about why the ancients thought that maths was of a different order of reality to sensory objects, this is more or less all I saw. Subsequently I've pursued the theme as it developed, and then more or less petered out in the late medieval period (save for the remaining mathematical platonists, of whom there are always some.) -
 Jamal
11.6kI think instead of saying math isn't in space and time we should say that math methodically ignores the actual, local spatial and temporal situation — green flag
Jamal
11.6kI think instead of saying math isn't in space and time we should say that math methodically ignores the actual, local spatial and temporal situation — green flag
I find that agreeable, but mathematical Platonism is rampant around here.
Are numbers and other abstract objects universals, and are universals real? Old questions.
Whatever the answers, I’m quite happy to say numbers and properties exist, along with thoughts and tables even in the case that they are abstract and dynamic. This is because to say that something exists isn’t to say all that much. It just sets things up (semi-literally) so you can deal with them. I see being in the same way. I can’t shake the thought that the controversies over what exists are motivated by a fear of irrelevance in the face of physical science. Otherwise, why worry?
EDIT: if there seems to be an anti-philosophical note at the end there, it’s just in the way of provocation. -
 Richard B
550The Pythagoreans were shocked to discover that the square root of 2 was irrational.It is an eternal fact that the square root of 2 cannot be expressed as a ratio of two whole numbers. That fact was true before the Pythagoreans discovered it and it will be true for all eternity. You seemed to be taking the Mathemetical Formalism route, which is a minority position among working mathematicians, most of whom accept Mathematical Platonism. — Art48
Richard B
550The Pythagoreans were shocked to discover that the square root of 2 was irrational.It is an eternal fact that the square root of 2 cannot be expressed as a ratio of two whole numbers. That fact was true before the Pythagoreans discovered it and it will be true for all eternity. You seemed to be taking the Mathemetical Formalism route, which is a minority position among working mathematicians, most of whom accept Mathematical Platonism. — Art48
From Wittgenstein's "Remarks on the Foundation of Mathematic"
I 168, "The mathematician is aninventor, not a discoverer."
II 2 "But the mathematician is not a discoverer: he is aninventor."
II 38 "From the fact, however, that we have an employment for a kind of numeral which, as it were, gives the number of the members of an infinite series, it does not follow that it also makes some kind of sense to speak of the number of the concept 'infinite series'; that we have here some kind of employment for something like a numeral. For there's no grammatical technique suggesting employment of such an expression. For I can of course form the expression: "class all classes which are equinumerous with the class 'infinite series'" (as also: "class of all angels that can get on to a needlepoint") but this expression is empty so long as there is no employment for it. Such an employment is not: yet to be discovered, but: still to be invented."
V 11 "If you want to know more about the series, you have, so to speak, to get into another dimension (as it were from the line into a surrounding plane).-But then isn't the plane there, just like the line, and merely something to be explored, if one want to know what the facts are? No, the mathematics of this further dimension has to be invented just as much as any mathematics."
From Wittgenstein's Lectures on the foundations of Mathematic
"One talks of mathematical discoveries. I shall try again and again to show that what is called a mathematical discovery had better be called a mathematical invention. In some of the cases to which I point, you perhaps be inclined to say, "Yes they had better be calledinventions"; in other cases you may perhaps be inclined to say, "Well, it is difficult to say whether in this case something has been discovered or invented."
Wittgenstein's position is an outcomes of his later views on language and meaning, exploring how these symbols become "alive with meaning." For him, Platonic views of mathematics lack utility due to offering no explanatory power and leading to confusion. -
 Wayfarer
26kwhy worry? — Jamal
Wayfarer
26kwhy worry? — Jamal
Thomists and other critics of Ockham have tended to present traditional [i.e. 'scholastic'] realism with its forms or natures, as the solution to the modern problem of knowledge. It seems to me that it does not quite get to the heart of the matter. A genuine realist should see “forms” not merely as a solution to a distinctly modern problem of knowledge, but as part of an alternative conception of knowledge, a conception that is not so much desired and awaiting defense, as forgotten and so no longer desired. Characterized by forms, reality had an intrinsic intelligibility, not just in each of its parts but as a whole. With forms as causes, there are interconnections between different parts of an intelligible world, indeed there are overlapping matrices of intelligibility in the world, making possible an ascent from the more particular, posterior, and mundane to the more universal, primary, and noble.
In short, the appeal to forms or natures does not just help account for the possibility of trustworthy access to facts, it makes possible a notion of wisdom, traditionally conceived as an ordering grasp of reality. — Joshua Hochschild - What's Wrong with Ockham? -
 Jamal
11.6kSo there’s a scale of thingyness and an independent scale of abstractness. — Jamal
Jamal
11.6kSo there’s a scale of thingyness and an independent scale of abstractness. — Jamal
I like considering more than one dimension. — green flag
Two might not be enough but it's better than one, so I made a 2D ontology chart, without much thought as to how pointless or wrongheaded it might be.
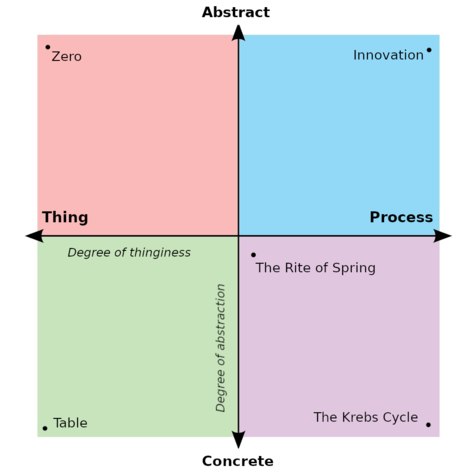
-
 Art48
498We will probably never stop trying to figure out exactly what an idea is (what we mean by 'idea.'). I think they exist (whatever exactly that means), and I think they are at least like blurry equivalence classes. — green flag
Art48
498We will probably never stop trying to figure out exactly what an idea is (what we mean by 'idea.'). I think they exist (whatever exactly that means), and I think they are at least like blurry equivalence classes. — green flag
I don’t see how ideas can be equivalence classes because the elements of an equivalence class are logically prior to the class. For instance, the integers are logically prior to the even numbers. For 2 to be a member of the equivalence class of even numbers, 2 must already exist/subsist/be defined/etc. The elements of a set are logically prior to the set (aside from sets defined self-referentially. But such sets lead to logical problems, for example, the set of all sets.) -
 Art48
498
Art48
498
Try shaking harder. :) These questions were discussed long before science existed and are interesting in themselves. P.S. I like your chart of thing/process, abstract/concrete.I can’t shake the thought that the controversies over what exists are motivated by a fear of irrelevance in the face of physical science. — Jamal -
 Jamal
11.6kThese questions were discussed long before science existed and are interesting in themselves. — Art48
Jamal
11.6kThese questions were discussed long before science existed and are interesting in themselves. — Art48
As I said to Wayfarer, despite appearances what I was referring to was not so much ontology as such, or the problem of universals, degrees of reality in Platonism, and so on, but more about the motivations behind the particular ways these ideas appear in contemporary concepts, like the mindscape. -
 Jamal
11.6k... philosophy should seek its contents in the unlimited diversity of its objects. It should become fully receptive to them without looking to any system of coordinates or its so-called postulates for backing. It must not use its objects as the mirrors from which it constantly reads its own image and it must not confuse its own reflection with the true object of cognition. — Adorno, Lectures on Negative Dialectics
Jamal
11.6k... philosophy should seek its contents in the unlimited diversity of its objects. It should become fully receptive to them without looking to any system of coordinates or its so-called postulates for backing. It must not use its objects as the mirrors from which it constantly reads its own image and it must not confuse its own reflection with the true object of cognition. — Adorno, Lectures on Negative Dialectics
Here the significant dimension is concept/object, where the struggle is to get hold of objects without conceptualizing them. This is impossible to do in philosophy, but that's ok, because it's negative dialectics: it's trying to do what Wittgenstein said could not be done, though not with any naively hubristic metaphysical system.
From this perspective, an idea is a conceptual thing in a world of conceptual things called philosophy, or art or culture, or some other more granular "field of sense"--but the philosophical task is to uncover the real. This goes back to my first criticism: it's assumed by Adorno that the real is the material, whether the material is a table, or the relationship between an employer and an employee, or the freedom to flourish. And while these might have different strengths of conceptual flavour, that doesn't matter much, because this is historically relative and there is always in these cases something real in them. So probably the worst move to make is to try so hard to prove the realness of ideas that you invent a whole landscape out of them. That just confuses the concept/object dichotomy and reifies concepts unknowingly, thus obscuring the essential relationship between them. -
 plaque flag
2.7k
plaque flag
2.7k
As I said from the beginning, mathematical equivalence classes are only a metaphor for nonmathematical concepts. And even this was only a hypothesis, a path for exploration. Platonism has been found wanting, even if the news of its failure is ignored, so the issue is what to try next. -
 plaque flag
2.7kYes, there is an alternative to praying at the altar of Plato, it is appreciating human’s incredible ability to create a form of life like mathematics. — Richard B
plaque flag
2.7kYes, there is an alternative to praying at the altar of Plato, it is appreciating human’s incredible ability to create a form of life like mathematics. — Richard B
:up:
And let me add that folks don't hate Plato (necessarily) because they hate Jesus. They sometimes just care about truth, and Platonism doesn't work. To be fair, I know lots of math, and math is exactly the tiny slice of human thinking where Platonism is at least feasible. But leave that little crystal castle and it's a broken theory. -
 plaque flag
2.7kWhatever the answers, I’m quite happy to say numbers and properties exist, along with thoughts and tables even in the case that they are abstract and dynamic. This is because to say that something exists isn’t to say all that much. It just sets things up (semi-literally) so you can deal with them. I see being in the same way. I can’t shake the thought that the controversies over what exists are motivated by a fear of irrelevance in the face of physical science. — Jamal
plaque flag
2.7kWhatever the answers, I’m quite happy to say numbers and properties exist, along with thoughts and tables even in the case that they are abstract and dynamic. This is because to say that something exists isn’t to say all that much. It just sets things up (semi-literally) so you can deal with them. I see being in the same way. I can’t shake the thought that the controversies over what exists are motivated by a fear of irrelevance in the face of physical science. — Jamal
Yes to all of this. As I see it, a genuine alternative to scientism is something like hermeneutic phenomenology. Heidegger's reputation is justly wounded, but the kind of thing he does is the right cure for scientism. The lifeworld (just the world for those not locked in scientism) encompasses scientific discourse, religious discourse, etc. I guess the theme is holism. There's no attempt to reduce everything to one mind (God, matter, mind.)
Some versions of antiscientism end up looking like a competing variant. After all, the laws of physics are (for some) already the gleaming mind or essence of God. If only we can squeeze some ethics in there, some 'literary' stuff which is nevertheless timeless and safe from ambiguity. It looks to me like the same old flight from death and change and our fate of having to make it new again and again. Becker's vision of the Oedipus complex is like Nietzsche's will-to-power. If I can find the eternal and static mind of God, I become the Wise Man, the unmoved mover. I have beat the video game. And I might as well be dead. -
 plaque flag
2.7kFrom this perspective, an idea is a conceptual thing in a world of conceptual things called philosophy, or art or culture, or some other more granular "field of sense"--but the philosophical task is to uncover the real. This goes back to my first criticism: it's assumed by Adorno that the real is the material, whether the material is a table, or the relationship between an employer and an employee, or the freedom to flourish. And while these might have different strengths of conceptual flavour, that doesn't matter much, because this is historically relative and there is always in these cases something real in them. So probably the worst move to make is to try so hard to prove the realness of ideas that you invent a whole landscape out of them. — Jamal
plaque flag
2.7kFrom this perspective, an idea is a conceptual thing in a world of conceptual things called philosophy, or art or culture, or some other more granular "field of sense"--but the philosophical task is to uncover the real. This goes back to my first criticism: it's assumed by Adorno that the real is the material, whether the material is a table, or the relationship between an employer and an employee, or the freedom to flourish. And while these might have different strengths of conceptual flavour, that doesn't matter much, because this is historically relative and there is always in these cases something real in them. So probably the worst move to make is to try so hard to prove the realness of ideas that you invent a whole landscape out of them. — Jamal
Matter is the shadow of mind is the shadow of matter. 'Pure' matter is as elusive and useless and canceling as 'pure' mind. I love Saussure for driving home the contrastive nature of language. Brandom emphasizes that we just can't understand one concept without understanding many. We are not thermostats. -
 Wayfarer
26kOne talks of mathematical discoveries. I shall try again and again to show that what is called a mathematical discovery had better be called a mathematical invention. — Wittgenstien - Richard B
Wayfarer
26kOne talks of mathematical discoveries. I shall try again and again to show that what is called a mathematical discovery had better be called a mathematical invention. — Wittgenstien - Richard B
I think the argument against this is the existence of mathematical constants. They are understood as providing objective and universal truths about the world. Unlike empirical observations, which are subject to error and variability, mathematical constants are immutable and universally applicable. For example, the golden ratio has been used as a symbol for beauty, proportion, and harmony. Pi has been used as a symbol for the infinite and the irrational. The 'six numbers' of Martin Rees, signifying the fundamental physical constraints without which matter would not have formed. The fact that mathematical physics has frequently predicted things about nature which observation alone could never do (and in the 20th c, empirical observations frequently took decades of development to test those predictions, Dirac's prediction of anti-matter being a paradigmatic example.) Claiming that these are mathematical inventions is, to say the least, rather anthropocentric, is it not? Yet it's the same ability that gave rise to these predictions that enabled the very technology on which you are now reading this.
When I ask what the number 7 is, you will point to the number, 7, and say that is what it is. But '7' is a symbol. That is an invention and can be represented in many different symbols: VII, SEVEN. What is not invented, is the meaning of the symbol. And that is what we all agree on.
Suddenly I can see what happened. Galileo saw the significance of dianoia - 'the book of the heavens is written in mathematics.' But Plato's ethics became assimilated into Christianity - and discarded with it. So we have all the engineering, but hardly any of the vision.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum





