-
 TonesInDeepFreeze
3.8kinfinity and infinite sets are also used in everyday language outside of set theory — RussellA
TonesInDeepFreeze
3.8kinfinity and infinite sets are also used in everyday language outside of set theory — RussellA
Since you are harkening to the original post, see that it is a question about the infinitude of intervals on the real number line, and about the number of different infinite sizes. The ordinary context of that is mathematics and set theory. Anyone is welcome to consider the question in another context, but that doesn't make it inapposite to talk about it in the context of mathematics and set theory.
As the OP doesn't refer to the very specific field of "set theory", having its own particular rules, I think the OP should be considered as a problem of natural language. — RussellA
That's a non sequitur. That the poster didn't mention set theory by name does not imply that set theory would not be a natural context for the matter, especially as the question gave a mathematical context and refers to a concept that is characteristically set theoretic. Moreover, discussion doesn't even have to be limited to whatever unstated context the poster himself might have had in mind.
Within natural language, the question "are there an infinite number of infinities" is meaningless — RussellA
If that is true, then even more reason why one would then consider the question in regard to mathematics. If it's meaningless in context C but defined in another context D, then it wouldn't make sense to say that then it is inapposite to context D. -
 RussellA
2.6kIf that is true, then even more reason why one would then consider the question in regard to mathematics. If it's meaningless in context C but defined in another context D, then it wouldn't make sense to say that then it is inapposite to context D. — TonesInDeepFreeze
RussellA
2.6kIf that is true, then even more reason why one would then consider the question in regard to mathematics. If it's meaningless in context C but defined in another context D, then it wouldn't make sense to say that then it is inapposite to context D. — TonesInDeepFreeze
That raises the interesting question that if an expression such as "infinite infinities" has no meaning in a natural language, the everyday spoken and written language used to describe the world around us, but does have meaning in the formal language of set theory, then what exactly is the relationship between a formal language such as set theory and the world around us? -
 Corvus
4.7k
Corvus
4.7k
You must read them yourself. They all had reservations on the concept of Infinity in math. Quite understandably and rightly so.What passages from Frege, Russell or Hilbert do you have in mind? — TonesInDeepFreeze -
 Corvus
4.7k
Corvus
4.7k
Sure as endeavours to be formal and more clear in their system, but is it always making sense? That is another question. Often it tends to make the system look more convoluted, if not done properly.Perhaps not axioms as the main approach. And philosophy ranges from poetic through speculative, hypothetical, concrete and formal. But deductive reasoning and demonstration is basic and ubiquitous in large parts of philosophy. And the axiomatic method does appear in certain famous philosophy, and its principles and uses - sometimes even formalized - are prevalent in modern philosophy, philosophy of mathematics and philosophy of language. — TonesInDeepFreeze
Objectivity is the objectivity of knowledge. Not objectivity of philosophy or objectivity of mathematics. That is another misunderstanding of yours. I wouldn't be surprised if you go on claiming an objectivity for set theories and an objectivity for numbers ... It is like saying a subjectivity of objectivity. A contradiction.But when I mentioned objectivity, of course I was not referring to objectivity of philosophy, but rather the objectivity of formal axiomatics, in the very specific sense I mentioned. And that is a philosophical consideration. Then you challenged my claim that mathematics has that objectivity. So I explained to you again the very specific sense I first mentioned. The fact that philosophy in its wide scope is not usually characterized as axiomatic doesn't vitiate my point. — TonesInDeepFreeze -
 RussellA
2.6kIn your first question, "a person who can speak English" is a description, not an object. — Metaphysician Undercover
RussellA
2.6kIn your first question, "a person who can speak English" is a description, not an object. — Metaphysician Undercover
Can there be a description without an object being described?
Isn't "a person who can speak English" a description of the object (a person who can speak English)?
===============================================================================
It is not a true representation of how we use numbers, to think of a number as itself an object. — Metaphysician Undercover
The word "object" has different meanings. In mathematics, a mathematical object is an abstract concept (Wikipedia – Mathematical Object). In natural language, it can be something material perceived by the senses (Merriam Webster - Object).
For example, we can think of the number , the number and as abstract mathematical objects but cannot think of them as natural concrete objects.
However we can think of the numbers 1. 6 and 10 as not only abstract mathematical objects but also as natural concrete objects.
That raises the question as to how we are able to think of something that is abstract, disassociated from any specific instance (Merriam Webster – Abstract). For example, independence, beauty, love, anger, Monday, , and the number 6.
George Lakoff and Mark Johnson in their book Metaphors We Live By propose that we can only understand abstract concepts metaphorically, in that we understand the concept of gravity by thinking about a heavy ball on a rubber sheet.
Thereby, we understand the concept of independence by remembering the feeling of leaving a job we didn't like. We understand the concept of beauty by looking at a Monet painting of water-lilies. We understand the concept of infinity by thinking about continually adding to an existing set of objects. We understand the concept of by thinking about the number 1.414 etc etc. We understand the concept of 6 by picturing 6 apples.
IE, we can only understand an abstract concept metaphorically, whereby a word or phrase literally denoting one kind of object or idea is used in place of another to suggest a likeness or analogy between them (Merriam Webster – Metaphor). -
 Corvus
4.7k
Corvus
4.7k
Axiomatic methodology in math is not free from problems and deficiencies. They are subjective definitions which are often circular in logic. They lack in consistency and are incomplete in most times.As I said, there are deep, puzzling questions about mathematics, but that doesn't make the mathematics itself, especially as formalized, confusing. On the contrary, if you ever read a treatment of the axiomatic development of mathematics, you may see that it is precise, unambiguous, objective (in the specific sense I mentioned), and with good authors, crisply presented. — TonesInDeepFreeze
They are dependent on the other axioms mostly. Most of them are abstract and illusional which renders to the false conclusions. A typical example is the Infinity in Set theory. -
 Metaphysician Undercover
14.7kCan there be a description without an object being described? — RussellA
Metaphysician Undercover
14.7kCan there be a description without an object being described? — RussellA
Of course, that's known as fiction.
However we can think of the numbers 1. 6 and 10 as not only abstract mathematical objects but also as natural concrete objects. — RussellA
This evades me. How do you think of a number as a natural concrete object? Are you talking about the numeral, or the group of objects which the numeral is used to designate, or what?
That raises the question as to how we are able to think of something that is abstract, disassociated from any specific instance (Merriam Webster – Abstract). For example, independence, beauty, love, anger, Monday, ∞
∞
, 2–√
2
and the number 6.
George Lakoff and Mark Johnson in their book Metaphors We Live By propose that we can only understand abstract concepts metaphorically, in that we understand the concept of gravity by thinking about a heavy ball on a rubber sheet.
Thereby, we understand the concept of independence by remembering the feeling of leaving a job we didn't like. We understand the concept of beauty by looking at a Monet painting of water-lilies. We understand the concept of infinity by thinking about continually adding to an existing set of objects. We understand the concept of 2–√
2
by thinking about the number 1.414 etc etc. We understand the concept of 6 by picturing 6 apples.
IE, we can only understand an abstract concept metaphorically, whereby a word or phrase literally denoting one kind of object or idea is used in place of another to suggest a likeness or analogy between them (Merriam Webster – Metaphor). — RussellA
So why would we label an abstract concept an "object", as in "mathematical object", and speak of it as if it had an identity in the same way that a natural concrete object has an identity? If we only know abstract concepts through analogy, or suggestions of likeness, isn't it completely wrong to suggest that anything which only exists in this way, i.e. through metaphor, could have an "identity"?
This is the problem which @TonesInDeepFreeze is stuck on. Tones seems to think that just because one can show how "=" can be used to to show a relationship of identity between two distinct names for the same natural concrete object (]Mark Twain = Samuel Clemens), we can conclude that when "=" is used in mathematics, it's being used in that same way.
But of course in mathematics this is not true. There is no such natural concrete object which the symbols refer to, in theory. only abstract concepts. Natural concrete objects are only referred to through application. And in application the concrete situation referred to by the right side of the equation is never the same as the concrete situation referred to by the left side. So all that Tones has indicated is that there is two very different ways to use "=", the mathematical way, and the way which signifies a relation between two different names for the same natural concrete object. Therefore, we must be careful not to confuse the two different ways, or equivocate between them, because that would be misleading. -
 Corvus
4.7k
Corvus
4.7k
That was an accurate description of the problems of the mathers. Not blindly punching anything at all.No matter what the textbooks say, one must be able to ask Why? instead of just blindly accepting the answers and claim that it is the only truths because the textbooks say so.
— Corvus
Again, you are unfamiliar with any of this; you are blindly punching. — TonesInDeepFreeze
The other shortcomings of math is it cannot accurately reflect the real world and its problems. It often distorts it via the unfounded and unjustified concepts and axioms, hence arriving at nonsense.
Mind you when math started in ancient Egypt, it used to be for mainly the practical problem solving purposes e.g. counting the sheeps, cows, and apples in the markets, and finding out the boundaries and locations for the pyramid locations in the deserts.
It used to work well, but once math started running the blind free rein of modifying the abstract concepts and keep deducing the illusional theories, things started going wrong turning the empirical and pragmatic skills in origin into some sort of an abstract subject which sometimes speaks in the tone of deeply frozen religion. Not cool at all. -
 RussellA
2.6kOf course, that's known as fiction. — Metaphysician Undercover
RussellA
2.6kOf course, that's known as fiction. — Metaphysician Undercover
"A mythical animal typically represented as a horse with a single straight horn projecting from its forehead" describes an object, even through the object is fictional.
In fact, from my position of Neutral Monism, all objects, whether house, London, mountain, government, the Eiffel Tower, unicorn or Sherlock Holmes are fictional, in that no object is able to exist outside the mind and independently of the mind.
===============================================================================
How do you think of a number as a natural concrete object? Are you talking about the numeral, or the group of objects which the numeral is used to designate, or what? — Metaphysician Undercover
The problem is, how does the mind understand an abstract concept, such as beauty, , ngoe, or the number 6?
My belief is that the mind cannot understand an abstract concept in isolation from concrete instantiations of it, in that, if I am learning a new word, such as "ngoe", it would be impossible to learn its meaning in isolation from concrete instantiations of it.

IE, I see no possibility of learning an abstract concept, such as "ngoe" or the number "6" without first being shown concrete examples of it.
===============================================================================
There is no such natural concrete object which the symbols refer to, in theory. only abstract concepts. — Metaphysician Undercover
If I wanted to teach you the meaning of the symbol "ngoe", which I know is a concept, how is it possible for you to learn its meaning without your first being shown particular concrete instantiations of it?
===============================================================================
And in application the concrete situation referred to by the right side of the equation is never the same as the concrete situation referred to by the left side. — Metaphysician Undercover
Given 1 and 1, if the second use of 1 refers to the same thing as the first use of 1, then the proper equation should be 1 = 1. The symbol "=" means identity
Given 1 and 1, if the second use of 1 refers to a different thing as the first use of 1, then the proper equation should be 1 + 1 = 2. The symbol "=" means equality.
Continuing:
Given a horse's body and a horse's head, as a horse's body is different to a horse's head, the proper equation should be horse's body + horse's head = horse
This raises the question as whether a horse as a whole is more than the sum of its parts, a horse's body and a horse's head.
Has the whole emerged from its parts, or is the whole no more than the sum of its parts?
IE, by knowing the parts, can I of necessity know the whole?
Referring back to Kant, by knowing the parts, for example, the number 5 and the number 7, can I of necessity know the number 12? -
 Lionino
2.7kStill follows grammatical rules just fine — Vaskane
Lionino
2.7kStill follows grammatical rules just fine — Vaskane
Niet, artistic freedom is fine, but "In passing I had caught a glimpse of the infinity beauty deep within her eyes" does not have "infinity" as an adjective, because the word can't be used as such, the sentence in fact comes across as gibberish. A good way to distinguish adjectives from nouns is putting them in an is-clause.
A: The world is infintiy.
B: The world is infinite.
If the predicate is giving a property to the subject, it is an adjective (B); if it is equating the predicate and the subjective, it is a noun (A).
And if you knew a bit about English history, you'd know the rules for English grammar died in 1066, and it mostly became about WORD ORDER — Vaskane
I would rather say that English was born in the late 11th century, with word order being the king that dictates meaning, but word order does not differentiate a noun from an adjective, since compound open nouns look syntactically identical to an adjective+noun, simply a word next to the other without any affixes, declination, or conjuctions.
Grammar itself includes word order, also known as syntax, you may be referring to morphology as "grammar", which is how the Greeks use it, and it is their words, so point to you. -
 Lionino
2.7kI bet if you put the cyber equivalent of a ravenous rat in its face like in '1984' then you could break it. Would say anything, begging like HAL 9000. — TonesInDeepFreeze
Lionino
2.7kI bet if you put the cyber equivalent of a ravenous rat in its face like in '1984' then you could break it. Would say anything, begging like HAL 9000. — TonesInDeepFreeze
I have no proof for my claims, but I remember using character.ai in early 2023 and I was concerned because that thing was smarter, more engaging, and more polite than the average person, and I spent days talking to the different characters despite there being people around me — not very well-mannered of me I reminisce. But I strongly feel that the AI there was downgraded and made dumber on purpose; I feel like free ChatGPT was also limited at around that time, I have not tried ChatGPT 4 yet. -
 Lionino
2.7k
Lionino
2.7k
Ironic, I was just using ChatGPT and it triple messed up:

https://chat.openai.com/share/96378835-0a94-43ce-a25b-f05e5646ec40 -
 Mark Nyquist
783It is useful to know the difference between a fixed mathematical object and a defined mathematical object.
Mark Nyquist
783It is useful to know the difference between a fixed mathematical object and a defined mathematical object.
Fixed would be things like pi, e, i, √2, √3.....
Defined would be things like variables, parameters, objects by unrestricted definition.
Infinity should always be regarded as a defined object and never a fixed object. -
 Lionino
2.7kYou're obviously not someone who has ever thought about writing in general — Vaskane
Lionino
2.7kYou're obviously not someone who has ever thought about writing in general — Vaskane
Wrong assumption.
A basic high school advanced composition class should teach you these things. It's fairly common knowledge. — Vaskane
Fortunately my high school was not somewhere where this is taught as poetry:

So I will do fine without the "self-expression" that amounts to the same sophistication as caveman paintings. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
The way it is done in ordinary formal mathematics is that there are open terms and closed terms.
Open terms have free variables. Closed terms have no free variables.
A constant is a closed term.
There are primitive closed terms and defined closed terms.
Before defining a constant, we must first prove there is a unique x such that x that satisfies a formula whose only free variable is x.
There are also primitive predicate symbols and defined predicate symbols.
An n-placed predicate symbol is defined by a formula having at most n free variables.
In set theory, there is no constant nicknamed 'infinity' (not talking about points of infinity on the extended real line and such here). Rather, there is the predicate nicknamed 'is infinite'. However we do define constants for certain infinite sets, such as [read 'w' here as if it were the Greek letter omega]:
x = w iff for alll y, y is a member of x iff y is a natural number. (The formula that is satisfied by one and only one x is "for all y, y is a member of x iff y is a natural number".) -
 TonesInDeepFreeze
3.8kTime, inclination and patience permitting, I hope to get caught up at some time to responding to the recent various misconceptions, non sequiturs, strawmen, etc. posted in this thread.
TonesInDeepFreeze
3.8kTime, inclination and patience permitting, I hope to get caught up at some time to responding to the recent various misconceptions, non sequiturs, strawmen, etc. posted in this thread. -
 Metaphysician Undercover
14.7k"A mythical animal typically represented as a horse with a single straight horn projecting from its forehead" describes an object, even through the object is fictional. — RussellA
Metaphysician Undercover
14.7k"A mythical animal typically represented as a horse with a single straight horn projecting from its forehead" describes an object, even through the object is fictional. — RussellA
I would definitely disagree with this. There is a big difference between seeing, hearing, touching, or otherwise sensing an "object", thereby describing what i sensed, and creating an imaginary "object". The latter does not involve an object, nor does it involve a "description" ( in the proper sense of the word) because it is an imaginary creation an invention rather than a description. A "fictional object" is not an object, that's actually what "fictional" means. OED #1 definition of object "a material thing that can be seen or touched". "Fictional", on the other hand, means exactly the opposite, invented by the imagination, therefore not able to be seen or touched.
In fact, from my position of Neutral Monism, all objects, whether house, London, mountain, government, the Eiffel Tower, unicorn or Sherlock Holmes are fictional, in that no object is able to exist outside the mind and independently of the mind. — RussellA
I suggest that your "position" is not consistent with common understanding. It might benefit you to give up on the monism.
My belief is that the mind cannot understand an abstract concept in isolation from concrete instantiations of it, in that, if I am learning a new word, such as "ngoe", it would be impossible to learn its meaning in isolation from concrete instantiations of it. — RussellA
There is no such thing as a "concrete instantiation" of a concept. Concepts are categorically different from concrete objects. To take your example, show me where I can find a concrete instantiation of beauty, 6, or the square root of 2. It is one thing to assert that there is a concrete instantiation of a six out there somewhere, but quite another thing to prove this. And if it is true, it ought to be easy to prove. Just point out this 6 to me, so i can go see it with my own eyes, or otherwise sense it.
If I wanted to teach you the meaning of the symbol "ngoe", which I know is a concept, how is it possible for you to learn its meaning without your first being shown particular concrete instantiations of it? — RussellA
This seems to be completely inconsistent with what you've already argued. You've already made the claim that you can make a fictious description, so why couldn't you also define a concept, thereby providing the means for someone else to understand it, without showing a concrete instance of that type of thing? I mean, you presented me with "a horse with a single straight horn projecting from its forehead", and i understand this image without seeing a concrete instantiation, so why take the opposite position now, and say that a person cannot understand the meaning of a concept without being shown a concrete instantiation of it.?
Given 1 and 1, if the second use of 1 refers to the same thing as the first use of 1, then the proper equation should be 1 = 1. The symbol "=" means identity
Given 1 and 1, if the second use of 1 refers to a different thing as the first use of 1, then the proper equation should be 1 + 1 = 2. The symbol "=" means equality. — RussellA
If this is the case, then what you have shown is logical inconsistency in the use of "1". In the first case, the two instances of 1 must refer to the very same thing, and in the second case, the two 1's must refer to two different things. If we simply say "=" means equality, then there is consistency between your two examples. Furthermore, there is no practical advantage to designating "=" as meaning identical in the case of "1=1", so you're just proposing logical inconsistency for no reason. That is simply illogical, therefore not a fair representation of the logic of mathematics. -
 RussellA
2.6kA "fictional object" is not an object,............. OED #1 definition of object "a material thing that can be seen or touched". — Metaphysician Undercover
RussellA
2.6kA "fictional object" is not an object,............. OED #1 definition of object "a material thing that can be seen or touched". — Metaphysician Undercover
A fictional object sounds like an object.
The OED notes "There are 14 meanings listed in OED's entry for the noun object, four of which are labelled obsolete" and then says "purchase a subscription".
The Merriam Webster includes "something mental or physical toward which thought, feeling, or action is directed".
I think Cervantes would have had great difficulty in writing "Don Quixote" without being able to describe objects.
===============================================================================
I suggest that your "position" is not consistent with common understanding. — Metaphysician Undercover
I agree that if one stopped one hundred people at random in the street, only a few would know about philosophical Monism.
Examples of modern philosophers who were monists include Baruch Spinoza, Georg Wilhelm Friedrich Hegel, Arthur Schopenhauer, and Bertrand Russell (https://study.com)
===============================================================================
There is no such thing as a "concrete instantiation" of a concept......................show me where I can find a concrete instantiation of beauty, — Metaphysician Undercover

How can one learn a concept in the absence of a concrete instantiation of it?
For example, as a test, suppose you thought of a concept. In practice, how can you teach me its meaning without using concrete instantiations of it?
===============================================================================
Just point out this 6 to me, so i can go see it with my own eyes — Metaphysician Undercover
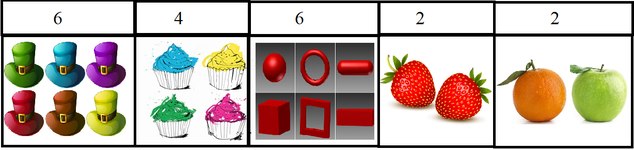
===============================================================================
I mean, you presented me with "a horse with a single straight horn projecting from its forehead", and i understand this image without seeing a concrete instantiation — Metaphysician Undercover
Exactly, you understand the concept using images.
===============================================================================
Furthermore, there is no practical advantage to designating "=" as meaning identical in the case of "1=1" — Metaphysician Undercover
There are two different cases.
The first a case of identity where the two 1's refer to the same thing. The second a case of equality where the two 1's refer to different things.
The practical advantage of using identity rather than equality is to distinguish two very different cases. -
 ssu
9.7kI think there is still a lot for us to understand about infinity.
ssu
9.7kI think there is still a lot for us to understand about infinity.
One reason that comes to my mind is that we haven't gotten much applied use for Aleph-2, for Aleph-3, or Aleph-4 etc. Usually correct math has a lot of applications. Physics and engineering and science uses it all the time. Cantor doesn't help it with then speaking of an Absolute Infinity. Now people dismiss this as irrelevant and just being Cantor's religious ideas (that God is Absolute Infinity), yet I don't think so. He simply didn't understand it and didn't get that kind of relevation as he did with noticing that the cardinality of the natural numbers isn't the same as with real numbers.
Yet once you assume that there actually would be theorem for Absolute Infinity that we haven't discover, then that theorem has to clear Russel's Paradox, the 'set of all sets', or the sometimes called Cantor's Paradox or Burali-Forti Paradox. When we have a paradox, obviously our reasoning about the premises aren't correct. Because mathematics is logical.
I think the problem is in counting itself and giving a proof in Mathematics. Mathematics has started from a need to count, not from let's create a logical system and call it math. Hence humans have made discoveries in math: that there are irrational numbers. That there are many types of geometries. Hence we can come up with new ways to think about math.
I'm not sure if this is correct, so I'll ask here: is counting basically a way to give a proof? Because let's assume that we have true but unprovable entities in Math (or with counting, uncountable numbers). What would you get if you would try to prove and unprovable entity in Math?
I guess you would get a paradox, because you cannot prove the unprovable or count the uncountable. The paradoxical nature is quite obvious. And the problem won't go away even with Cantor's hierarchial system.
Perhaps the problem is that people have tried to solve the paradoxes yet still hold on to their premises, as if everything is already there in the foundations of math and paradoxes can be kept away by restrictions. Like ZF.
I'm not saying that I know the answer, but saying that there might be here something for us to still discover. -
 Michael
16.6kI wonder if mathematical realists and mathematical antirealists have different views about mathematical infinity. I'm a mathematical antirealist. I have no problem with mathematical infinity. The "existence" of infinite sets does not entail the existence of infinities in nature (whether material or Platonic).
Michael
16.6kI wonder if mathematical realists and mathematical antirealists have different views about mathematical infinity. I'm a mathematical antirealist. I have no problem with mathematical infinity. The "existence" of infinite sets does not entail the existence of infinities in nature (whether material or Platonic). -
 Metaphysician Undercover
14.7kExactly, you understand the concept using images. — RussellA
Metaphysician Undercover
14.7kExactly, you understand the concept using images. — RussellA
The key point here, is that imagination does not require sensation of whatever it is that is imagined. But you claim understanding a concept requires "concrete instantiation" and I assume that means something which is sensed. If I'm wrong here, and "concrete instantiation" means the production of an image in the mind, without the requirement of sensing it, then we might have something to discuss.There are two different cases.
The first a case of identity where the two 1's refer to the same thing. The second a case of equality where the two 1's refer to different things.
The practical advantage of using identity rather than equality is to distinguish two very different cases. — RussellA
Yeah sure, you've indicated that in the first case "=" signifies identity. I agree, that's what you've stipulated. The point though, is that in the case where you used "=" to signify identity, it is not a mathematical usage. The "practical advantage" you refer to is rhetorical only, intended to persuade me. The usage is not mathematical, because in the application of mathematics "=" is not used to represent identity. That's the issue with Tones' example of Twain = Clemens, it just demonstrates that it's possible to use "=" in this way. However, it doesn't at all represent how people applying mathematics actually use "=" in the formulation of equations. So it's nothing but a rhetorical example, produced solely for the purpose of trying to persuade, in the mode of sophistry. -
 Metaphysician Undercover
14.7kI wonder if mathematical realists and mathematical antirealists have different views about mathematical infinity. I'm a mathematical antirealist. I have no problem with mathematical infinity. The "existence" of infinite sets does not entail the existence of infinities in nature (whether material or Platonic). — Michael
Metaphysician Undercover
14.7kI wonder if mathematical realists and mathematical antirealists have different views about mathematical infinity. I'm a mathematical antirealist. I have no problem with mathematical infinity. The "existence" of infinite sets does not entail the existence of infinities in nature (whether material or Platonic). — Michael
The issue is with the premises (axioms) of set theory. If you are "mathematical antirealist" you ought to reject set theory on the basis of the axioms it employs. Your view on "infinity" would be irrelevant at this point. So how set theory treats "infinite" would not even enter into the reasons for your rejection of it.
Set theory is based in the assumption of "mathematical objects". And, the mathematical objects as elements of the sets, are allowed to have relations which physical objects, according to our knowledge of them, cannot have. So a "set" by set theory is a bunch of "objects", but since they are mathematical objects instead of physical objects, what can be 'truthfully' said (what is acceptable by the axioms) about that bunch of objects, doesn't have to be consistent with our knowledge of physical objects. So for example, there can be an empty set (a bunch of objects with no objects), and sets do not necessarily have an order (a bunch of objects without any order to them). -
 Michael
16.6kIf you are "mathematical antirealist" you ought to reject set theory on the basis of the axioms it employs. — Metaphysician Undercover
Michael
16.6kIf you are "mathematical antirealist" you ought to reject set theory on the basis of the axioms it employs. — Metaphysician Undercover
Why? -
 Metaphysician Undercover
14.7kWhy? — Michael
Metaphysician Undercover
14.7kWhy? — Michael
Set theory begins with the assumption of mathematical objects, hence it is based in Platonic realism. -
 Michael
16.6kSet theory begins with the assumption of mathematical objects, hence it is based in Platonic realism. — Metaphysician Undercover
Michael
16.6kSet theory begins with the assumption of mathematical objects, hence it is based in Platonic realism. — Metaphysician Undercover
You don't need to believe in Platonic realism to use set theory. Its axioms are just rules to follow when "doing" maths. There's no need to think of them as statements that correspond to some mind-independent fact about the world.
In some set theories, sets can contain themselves. In others, they can't. As a mathematical antirealist I wouldn't claim that one of them must be "wrong". They're just following different rules. -
 Metaphysician Undercover
14.7kYou don't need to believe in Platonic realism to use set theory. — Michael
Metaphysician Undercover
14.7kYou don't need to believe in Platonic realism to use set theory. — Michael
I agree. I didn't say you need to believe in the truth of the principles you employ. However, it's hypocrisy to say "I'm a mathematical antirealist" and then go ahead and use set theory. But that sort of hypocrisy is extremely commonplace in our world, it's actually become the norm now. Very few people make the effort to understand the metaphysics which they claim to believe in, and whether it is consistent with the metaphysics which supports the theories which they employ in practise. -
 Michael
16.6kHowever, it's hypocrisy to say "I'm a mathematical antirealist" and then go ahead and use set theory. — Metaphysician Undercover
Michael
16.6kHowever, it's hypocrisy to say "I'm a mathematical antirealist" and then go ahead and use set theory. — Metaphysician Undercover
No it's not. -
 Michael
16.6kAnd how would you justify that claim? — Metaphysician Undercover
Michael
16.6kAnd how would you justify that claim? — Metaphysician Undercover
I already did above. The axioms of some given set theory are just rules that you must follow when using that set theory. Different set theories have different axioms and so different rules. Given that there's no connection between using some set theory and believing in the mind-independent existence of abstract mathematical objects, there's no hypocrisy in using some set theory and being a mathematical antirealist.
Your position is like arguing that it's hypocritical to play chess if I do not believe that the rules of chess correspond to some mind-independent fact about the world.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum










