-
 flannel jesus
2.9k
flannel jesus
2.9k
I would like to have a discussion with Corvus about if the logic used here is actually logical, or if it is perhaps fallacious.
Much later in that thread, it was acknowledged that it's not Modus Ponens, so we can agree on that. So if it's not Modus Ponens, the remaining question I had was, can you, in general, go from a statement of the form A -> B to ~A -> ~B - the answer to this is still up in the air, so that's the next thing to clarify.
Corvus, can you go from any statement of the form A -> B to ~A -> ~B, OR are there statements of the form A -> B where you can't reasonably go to ~A -> ~B?
Or, more succinctly, does (A -> B) -> (~A -> ~B) all the time, for all statements of implication A -> B?
I believe we can resolve this. -
 flannel jesus
2.9kif you agree with corvus, I wouldn't mind talking to you about why.
flannel jesus
2.9kif you agree with corvus, I wouldn't mind talking to you about why.
If you disagree, it would be appreciated if you expressed briefly why but, ideally, exited the thread after that to avoid too many overlapping debates and confusion.
If corvus has other preferences, I welcome him to express them and hopefully they can be accommodated. -
 Corvus
4.8kLogic is a science of inference. That is one of my old logic book says. To prove a statement for true or false, you must start with a premise to prove, then make the relevant inference. (Don't make irrelevant nonsensical inferences such as hosing a garden into this argument, and you get told, are you having a laugh mate?)
Corvus
4.8kLogic is a science of inference. That is one of my old logic book says. To prove a statement for true or false, you must start with a premise to prove, then make the relevant inference. (Don't make irrelevant nonsensical inferences such as hosing a garden into this argument, and you get told, are you having a laugh mate?)
If it rains, then the ground will be wet. (Premise to prove)
R -> W
If it doesn't rain, then the ground will not be wet. (Inference = WHY NOT??)
Not R -> Not W
At this moment, you check to see if it rains, and if the ground is wet in reality.
It doesn't rain, and the ground is not wet. (TRUE from the inspection and observation)
Not R -> Not W = True
Therefore If it rains, then the ground will be wet. (True)
R -> W
Therefore for proving A->B is true or false, Not A -> Not B premise works fine.
You can use a proof based on the Truth table too.
R | W | R and W | R or W | R-> W | NotR | NotW | NotR -> NotW
T | T | T | T | T | F | F | T
T | F | F | T | F | F | T | T
F | T | F | T | T | T | F | F
F | F | F | F | T | T | T | T -
 flannel jesus
2.9kWould you mind explicitly stating if every (a implies b) also leads to (not a implies not b), or can you only do that for specific (a implies b) statements?
flannel jesus
2.9kWould you mind explicitly stating if every (a implies b) also leads to (not a implies not b), or can you only do that for specific (a implies b) statements?
Are there any exceptions? -
 Corvus
4.8kThe truth table value is from the rule. But you also check with the reality observations here too, because it is an empirical argument, not analytic.
Corvus
4.8kThe truth table value is from the rule. But you also check with the reality observations here too, because it is an empirical argument, not analytic. -
 flannel jesus
2.9kThat sounds like you're confirming that yes, it's always applicable any time you have (a implies b), am I interpreting that correctly?
flannel jesus
2.9kThat sounds like you're confirming that yes, it's always applicable any time you have (a implies b), am I interpreting that correctly? -
 Corvus
4.8kI think you are correct. But you don't have to always apply the contradiction. It depends on the case, and your inference.
Corvus
4.8kI think you are correct. But you don't have to always apply the contradiction. It depends on the case, and your inference. -
 flannel jesus
2.9kDo you also agree with the contrapositive rule, which states that if (a implies b), then (not b implies not a)?
flannel jesus
2.9kDo you also agree with the contrapositive rule, which states that if (a implies b), then (not b implies not a)? -
 flannel jesus
2.9kdo you have examples where it doesn't apply?
flannel jesus
2.9kdo you have examples where it doesn't apply?
Examples of a implies b where is not true that not b implies not a -
 Corvus
4.8kdo you have examples where it doesn't apply? — flannel jesus
Corvus
4.8kdo you have examples where it doesn't apply? — flannel jesus
If not sure, make up an extended truth table for all the possible scenarios, and see all the cases for the TF values. It gets apparent. -
 flannel jesus
2.9kwait you edited this response, we have to go back. We need clarity on this conversation or nothing will work.
flannel jesus
2.9kwait you edited this response, we have to go back. We need clarity on this conversation or nothing will work.
It either always applies, or it doesn't always apply. When you say you think I'm right, that means it always applies. But then you say it depends on the case. It either always applies, or it depends on the case, it can't be both. -
 Corvus
4.8kIt is not "lead to". It is an assumption, which you bring into the argument that you think most relevant and reasonable for the premise that you want to prove. But the truth table contains all the cases and TF values. If it is an empirical case, you must check with the reality for the TF values for the real TF values.
Corvus
4.8kIt is not "lead to". It is an assumption, which you bring into the argument that you think most relevant and reasonable for the premise that you want to prove. But the truth table contains all the cases and TF values. If it is an empirical case, you must check with the reality for the TF values for the real TF values. -
 Corvus
4.8kIn the case of If it rains the the ground will be wet. You think and infer, which will be most relevant and good to test, if it is true? Ah... how about if it doesn't rain, and the will not be wet? NotR -> NotW. And check it with the reality.
Corvus
4.8kIn the case of If it rains the the ground will be wet. You think and infer, which will be most relevant and good to test, if it is true? Ah... how about if it doesn't rain, and the will not be wet? NotR -> NotW. And check it with the reality.
But you can bring other assumptions as counter reasonings and inferences for the proof process. If not sure, make a truth table, insert all the TF values according to the rules. Ok, Later~ -
 flannel jesus
2.9kI think I misread this before. You're saying you "don't have to apply it", but you always can right? You CAN always apply it, because it's always true, you're just saying there's not always a contextual need to apply it, is that right?
flannel jesus
2.9kI think I misread this before. You're saying you "don't have to apply it", but you always can right? You CAN always apply it, because it's always true, you're just saying there's not always a contextual need to apply it, is that right?
So any time you have (a implies b) , it's always true that (not a implies not b), you just don't always need to bring that up. Is that what you're saying?
And is the same thing true about the contrapositive? For every (a implies b) it's always true that (not b implies not a), correct? Even if it's not always useful to bring it up, it's always true? -
 Corvus
4.8kEvery case in the truth value can be applied for your inference. If it helps to contrapositive for your argument, and it matches the reality event, then yes it can be adopted.
Corvus
4.8kEvery case in the truth value can be applied for your inference. If it helps to contrapositive for your argument, and it matches the reality event, then yes it can be adopted.
If you look closely the truth table, it only ever contains P and Q cases with various connectives and extensions. You never see in the table H -> W, once it started with P, Q. It tells you that in an argument, you don't bring in some unrelated cases and argue, the logic is incorrect. That is just sheer nonsense.
If you started with H, G in an argument, then it only have cases with H and G in the truth table. That is the rule No.1.
Ok, we are going out for a meal here. I am not sure if it is under determinism or freewill. Have a good day, and talk to you later for any other points. -
 flannel jesus
2.9kI need clear, unambiguous answers. Preferably Yes or No.
flannel jesus
2.9kI need clear, unambiguous answers. Preferably Yes or No.
One thing at a time
So do you think any time you have (a implies b) , it's always true that (not a implies not b), you just don't always need to bring that up. Is that what you're saying? -
 Corvus
4.8kYes, it is correct. You don't need to always bring in Not A -> Not B for your inference. It is totally under your discretion of your inference for the case. It could be any case in the truth table you can bring in as your inference.
Corvus
4.8kYes, it is correct. You don't need to always bring in Not A -> Not B for your inference. It is totally under your discretion of your inference for the case. It could be any case in the truth table you can bring in as your inference. -
 flannel jesus
2.9kYes, it is correct. — Corvus
flannel jesus
2.9kYes, it is correct. — Corvus
Awesome, and this one?
And is the same thing true about the contrapositive? For every (a implies b) it's always true that (not b implies not a), correct? Even if it's not always useful to bring it up, it's always true? -
 flannel jesus
2.9kif it depends, I would love to see some examples. I would love to see an example from you where the answer is "yes" and an example from you where the answer is "no".
flannel jesus
2.9kif it depends, I would love to see some examples. I would love to see an example from you where the answer is "yes" and an example from you where the answer is "no".
An example where a implies b, and not b implies not a,
and an example where a implies b, but it's not true that not b implies not a.
I'm especially interested in the second example. The first example is very agreeable. The second is much more tricky, I think. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
This is a pretty common example in logic textbooks, but it is not the case that if A -> B then ~A -> ~B. To see why, consider a lawn with a sprinkler system. A person sees it has not rained (~A), but then goes out to find the lawn is wet (B). This is possible because there are many ways for the lawn to get wet (B). If it rains, the lawn will be wet, but the lawn might also be wet for other reasons.
I know you disallowed hoses, sprinklers, etc., but in that case, when the only way for the lawn to get is from the rain (A), you should frame it as an iff/biconditional.
To get ~A -> ~B the starting premise would need to be "if and only if it rains (iff A) then the lawn will be wet (B),or A <->B. In such a case, B also implies A.
This would be "denying the antecedent."
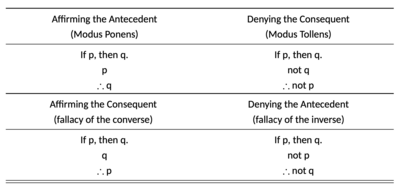
But Corvus seems to be assuming an iff relationship, in which case the inference would be valid. -
 bert1
2.2kFor every (a implies b) it's always true that (not b implies not a), correct? Even if it's not always useful to bring it up, it's always true? — flannel jesus
bert1
2.2kFor every (a implies b) it's always true that (not b implies not a), correct? Even if it's not always useful to bring it up, it's always true? — flannel jesus
It's always valid (if not true), and that's called modus tollens. You're right about that, but wrong about modus ponens.
EDIT: Sorry I seem to have misunderstood flannel jesus! I thought he was agreeing with Corvus, but after a PM exchange it's clear that he isn't. -
 Corvus
4.8kA person sees it has not rained (~A), but then goes out to find the lawn is wet (B). This is possible because there are many ways for the lawn to get wet (B). If it rains, the lawn will be wet, but the lawn might also be wet for other reasons. — Count Timothy von Icarus
Corvus
4.8kA person sees it has not rained (~A), but then goes out to find the lawn is wet (B). This is possible because there are many ways for the lawn to get wet (B). If it rains, the lawn will be wet, but the lawn might also be wet for other reasons. — Count Timothy von Icarus
The argument was meant to prove R -> W, not (R or H) -> W.
If you wanted to prove (R or H) -> W, then yes of course, the premise should have begun with it.
For (P1 ..... Pn)-> W, you would need to go into Higher Order logic, wouldn't you?
We were trying to probe P1 -> W, but if you bringing in P31-> W, then you would be brining in irrelevant inference into the argument.
IFF must be regarded as presumed in the argument looking at the starting premise from the number of variables in the premise i.e. 1. -
 flannel jesus
2.9k
flannel jesus
2.9k
Do you have an example for this?
An example where a implies b, but it's not true that not b implies not a.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum



