-
 Leontiskos
5.6kOk, so your "A without B" is not that "it is possible to have A without B", but that "there is A without B". I guess that can make sense as ¬(A→B) ↔ (A∧¬B). — Lionino
Leontiskos
5.6kOk, so your "A without B" is not that "it is possible to have A without B", but that "there is A without B". I guess that can make sense as ¬(A→B) ↔ (A∧¬B). — Lionino
The oddity is that there is not parity between a conditional and its negation:
it's intuitive that
A→B means not(A without B).
So it's intuitive that
¬(A→B) means A without B. — bongo fury
- A→B
- ¬(A→B)
A conditional, by its very name, signifies that which is not necessary. (1) is therefore conditional in that it neither commits us to A, ¬A, B, or ¬B. It retains something of the hypothetical nature of natural-language conditionals.
(2) is not a conditional in this sense, for it commits us to both A and ¬B.
In natural language when we deny a conditional we at the same time assert an opposed conditional; we do not make non-conditional assertions. In natural language the denial of a conditional is itself a conditional. But in propositional logic the denial of a conditional is a non-conditional.
See:
As noted in my original post, your interpretation will involve Sue in the implausible claims that attend the material logic of ~(A → B), such as the claim that A is true and B is false. Sue is obviously not claiming that (e.g. that lizards are purple). The negation (and contradictory) of Bob's assertion is not ~(A → B), it is, "Supposing A, B would not follow." — Leontiskos
Given material implication there is no way to deny a conditional without affirming the antecedent, just as there is no way to deny the antecedent without affirming the conditional. — Leontiskos
And:
You are thinking of negation in terms of symbolic logic, in which case the contradictory proposition equates to, "Lizards are purple and they are not smarter." Yet in natural language when we contradict or negate such a claim, we are in fact saying, "If lizards were purple, they would not be smarter." We say, "No, they would not (be smarter in that case)." The negation must depend on the sense of the proposition, and in actuality the sense of real life propositions is never the sense given by material implication. — Leontiskos
"If lizards were purple then they would be smarter."
The denial is, "Even if lizards were purple, they would not be smarter." It is not, "Lizards are purple and they are not smarter." The logical negation is the English counterexample.
---
The deeper issue here is that there is no uncontroversial way to translate between English and formal logic, because English has inherent meaning where logic has none. Logical meaning is derived from English meaning, and not vice versa. Because of this the "meaning" of a logical sentence is merely what can be done with it, or what it can be transformed into, and no one transformation is more central to its "meaning" than any other. This is what I was trying to get at on the first page.
Bongo did a good job of using English to capture the range of the logical possibilities, but at least one problem arises in that the English negation and the logical negation are substantially different. As you pointed out in the other thread, a central aspect of an English negation of a conditional is that the consequent and only the consequent is negated (e.g. If <lizards were purple> then NOT<lizards would be smarter>).
(What this then means is that to unequivocally claim that ' scenario does not represent a contradiction is to rely exclusively on a "bug" of material implication, and only those who are able to contextualize material implication within a larger whole will be able to consider the question more fully.) -
 Lionino
2.7k"Even if lizards were purple, they would not be smarter." — Leontiskos
Lionino
2.7k"Even if lizards were purple, they would not be smarter." — Leontiskos
My conclusion thus far is that «A does not imply B» can't be translated to logical language. I attempted several different ways in flannel jesus' thread but none worked.
In natural language when we deny a conditional we at the same time assert an opposed conditional; we do not make non-conditional assertions. In natural language the denial of a conditional is itself a conditional. But in propositional logic the denial of a conditional is a non-conditional. — Leontiskos
The problem is that the associativity of English words does not match the associativity of logical operators.
Like in math X(Y*W)=(X*Y)*W but X(Y+W)≠(X*Y)+W
Saying «A implies B» is A→B, but «A does not imply B» doesn't take the ¬ operator anywhere. An example is ¬(A→B∧¬B) can't be read as "It is not the case that A implies a contradiction", rather it is read as "not-A implies a contradiction", which is why that formula entails A. -
 Leontiskos
5.6kMy conclusion thus far is that «A does not imply B» can't be translated to logical language. — Lionino
Leontiskos
5.6kMy conclusion thus far is that «A does not imply B» can't be translated to logical language. — Lionino
Is there something wrong with: (A→¬B)?
(This is why I added a parenthetical edit to my last post, which is about the OP of the other thread.)
Saying «A implies B» is A→B, but «A does not imply B» doesn't take the ¬ operator anywhere. — Lionino
Yes, for it is not possible to capture the negation of the idiosyncrasies of material implication while simultaneously capturing the negation of the notion of implication or conditionality. One or the other must be lost. English abandons the first and propositional logic the second. -
 Leontiskos
5.6k- How is the logical statement different from the English statement «A does not imply B»?
Leontiskos
5.6k- How is the logical statement different from the English statement «A does not imply B»?
If B is always false whenever A is true, then surely «A does not imply B». The logic covers the English but the English is not captured by the logic. -
 AmadeusD
3.9k
AmadeusD
3.9k -
 Leontiskos
5.6k- Perhaps. I am thinking of the example that Janus gave elsewhere.
Leontiskos
5.6k- Perhaps. I am thinking of the example that Janus gave elsewhere.
P: Lizards are purple
S: Lizards are smarter
- (P→¬S)
- "P does not imply S"
I think the English sense is never falsified by the logical sense, and in that way it would seem to hold. The problem is that the logical sense can be falsified by alternative English senses, given that English has a more robust notion of implication than material implication. So you can't go in the other direction. Ergo, you cannot translate (P→¬S) as, "If lizards are purple, then they are (necessarily) not smarter," even though you can draw the conclusion, "P does not imply S" ("Lizards' purpleness does not imply lizards' smartness").
Edit: So we might say that (1) guarantees (2) but (2) does not guarantee (1). Thus I admit that it doesn't count as a real translation.
Edit2: I think Janus' argument is special insofar as it makes use of a Cambridge property, and in that case (1) and (2) seem to be the same. -
 Lionino
2.7kEdit: So we might say that (1) guarantees (2) but (2) does not guarantee (1). Thus I admit that it doesn't count as a real translation. — Leontiskos
Lionino
2.7kEdit: So we might say that (1) guarantees (2) but (2) does not guarantee (1). Thus I admit that it doesn't count as a real translation. — Leontiskos
:smile: -
 Leontiskos
5.6k
Leontiskos
5.6k
So then why is it that the logic cannot capture the English, "A does not imply B"? Is it because the English represents a denial without any corresponding affirmation?
If so, it seems that I was wrong when I said that to deny a conditional in English is necessarily also to affirm an opposed conditional:
In natural language when we deny a conditional we at the same time assert an opposed conditional — Leontiskos
In English we can deny in a manner that does not affirm the negation of any proposition, and this violates the way that propositional logic conceives of the LEM. In fact, going back to flannel’s thread, this shows that a contradiction in English need not take the form (A ^ ~A). In English one can contradict or deny A without affirming ~A.
...but then again maybe to say “Not A and not ~A” is only open to Buddhist-type logic or Buddhist-type English. Even if that is so, perhaps what is available more broadly is the denial of a consequence without any attendant affirmation, such as, “That does not follow from this, and I make no claim about what does follow,” as I claimed <here>. In this way one undercuts an inference and deprives the conclusion (or consequence) of its validity without falsifying the conclusion. Thus one can say, “A does not imply B,” without making any positive assertion, conditional or otherwise. Apparently the relation between a negation and an affirmation differs in English and in logic.
Edit: This may actually be key to understanding A→(B∧¬B), for the contradiction is nonsensical or unstable when taken in a particular sense, and this is why the standard logical operations cannot be applied to it in the same way. A reductio ad absurdum may be parallel to the English move of denying a conditional without affirming anything in the same move. If a reductio affirmed something in the same move then there would be no and-elimination step, and if that were so then a reductio would be identical to a modus tollens, which it is not. The affirmation involved as the final step of a reductio only takes place "after" the and-elimination step. The contradiction is repugnant regardless of which conjunct is preferred (or of which supposition was originally made), and this makes sense because what is proximately aimed at in a reductio is contradiction per se—a universal concept—rather than the application of any truth value to a variable. The application of the truth value to the variable is what is remotely aimed at, and will only take place after the contradiction and the and-elimination have already occurred. -
 Lionino
2.7kSo then why is it that the logic cannot capture the English, "A does not imply B"? — Leontiskos
Lionino
2.7kSo then why is it that the logic cannot capture the English, "A does not imply B"? — Leontiskos
I am starting to think that it is because the word "implies" has the idea of causality in it, while logic says nothing about causality. I reckon that it is better to think of a truth table as coexistence rather than causation.
For example, the truth table of A→B, it is false when A is true and B is false, it is true when both A and B are true. But does that mean that A implies B? A could true and so could B coincidentally, there could be no (causal) relationship between the two. So I think that when speaking of logic it is better to do away with "implies", which is causational — and by consequence also the "if A, B", which is just the word "imply" as a compound sentence — and use instead "not A without B", which is exactly understood in English as coexistence.
My last post on flannel's thread might be relevant.
In English one can contradict or deny A without affirming ~A. — Leontiskos
You mean that saying "He is not beautiful" is not necessarily the same as saying "He is ¬beautiful"? The difference between the two is often simply in the intonation that one speaks in. I think I brought that up in a comment in flannel's thread at some point. -
 Echarmion
2.7kMy conclusion thus far is that «A does not imply B» can't be translated to logical language. I attempted several different ways in flannel jesus' thread but none worked. — Lionino
Echarmion
2.7kMy conclusion thus far is that «A does not imply B» can't be translated to logical language. I attempted several different ways in flannel jesus' thread but none worked. — Lionino
Couldn't it be said that logical language establishes a number of precise connections between states, but the absence of a connection is not defined. It's the negative space that remains outside the ruleset. -
 bongo fury
1.8kIf
bongo fury
1.8kIf
So it's intuitive that
¬(A→B) means A without B. — bongo fury
doesn't follow from
it's intuitive that
A→B means not(A without B). — bongo fury
then it would seem that we don't intuit negation in this case as a photographic negative of the Venn diagram, which is what logic would deliver. In which, i.e., all previous no-go (shaded) areas are declared open for business, and all previous open regions are shaded out. Rather, the intuition is that a (in this case the) previous no-go area is opened up. But nothing closed off. We wish to withdraw or deny an assertion without thereby committing to its negative. Deny it is the case there won't be a sea battle, without claiming there will.
So, not really negation. Not cancelling out the first. Not restoring not(A without B) to A without B.
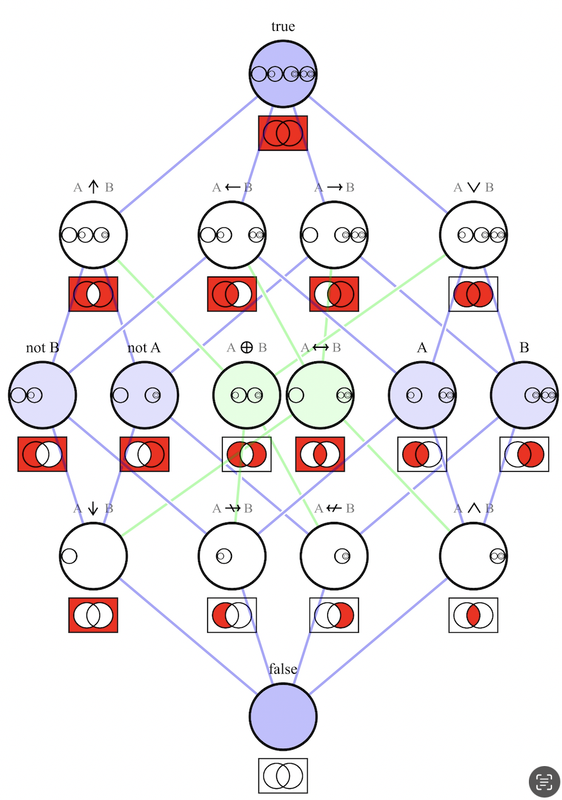
¬(A→B) appears to suggest, intuitively: maybe A without B, maybe not. No commitment. No information. Tautology. No shading in the Venn diagram. (Whose 4 non-overlapping areas correspond to A & B, A & ¬B, ¬A & B, ¬A & ¬B.)
Leaving it open. -
 Leontiskos
5.6kI am starting to think that it is because the word "implies" has the idea of causality in it, while logic says nothing about causality. I reckon that it is better to think of a truth table as coexistence rather than causation. — Lionino
Leontiskos
5.6kI am starting to think that it is because the word "implies" has the idea of causality in it, while logic says nothing about causality. I reckon that it is better to think of a truth table as coexistence rather than causation. — Lionino
Yep, I think this is right, and it's what I was trying to get at on the first page. I think my point about "denying without affirming a propositional negation" is also right, and Bongo developed that point. I wonder if the two can be brought together.
and use instead "not A without B", which is exactly understood in English as coexistence. — Lionino
In general I want to avoid thinking any English represents the logic, but I also I think this is a good point. But to give something of a counterexample, if A is false then we can say A→B, and yet your English does not capture this move. Thus:
Because of this the "meaning" of a logical sentence is merely what can be done with it, or what it can be transformed into, and no one transformation is more central to its "meaning" than any other. This is what I was trying to get at on the first page. — Leontiskos
Keeping to this counterexample, "not A without B" captures a truth-functional conditional, but it does not fully capture a material conditional. English involves "causation," but it additionally prescinds from the idiosyncrasies of the material conditional. I think Bongo's negation may have more to do with the materiality of the conditional than its lack of causation, although the two may well be related.
You mean that saying "He is not beautiful" is not necessarily the same as saying "He is ¬beautiful"? — Lionino
Ha - that's an additional consideration that I was not thinking of (Diotima's point in the Symposium). Prescinding from this question and from the question of Buddhist logic, my point is primarily about conditionals or consequences, and can be set out in response to Bongo:
We wish to withdraw or deny an assertion without thereby committing to its negative. Deny it is the case there won't be a sea battle, without claiming there will. — bongo fury
Basically, but more precisely, I would say that we are denying an inference. In English we don't usually say, "You are wrong that there will be a sea battle tomorrow, and yet there may be a sea battle tomorrow."* Instead we say, "Your reasoning for why there will be a sea battle tomorrow is not sound, and yet there may be a sea battle tomorrow."
N: There is a wind from the north tonight
S: There will be a sea battle tomorrow
N→S
The denial in English would seem to be, "S does not follow from N." This doesn't mean that S will always be false whenever N is true. It only means that S need not be true when N is true. This seems to be evidence for Lionino's view that a causal connection is at play. Or as I said on the first page, "The English has to do with a relation between P and Q that transcends their discrete truth values."
then it would seem that we don't intuit negation in this case as a photographic negative of the Venn diagram, which is what logic would deliver.
...
So, not really negation. Not cancelling out the first. — bongo fury
These are good thoughts, but I think a kind of cancelling-out is taking place. It's just that the denial transcends the limitations of truth-functional logic.
To deny something requires understanding what is first being asserted, that it might be denied. If someone says, "Wet grass follows from rain," they are not asserting everything that is involved in the logical claim <[rain]→[wet grass]>, for they are not asserting the idiosyncrasies of the material conditional, such as the idea that ~[rain] justifies their claim. At the same time, they are asserting something more than the logical claim insofar as they do not believe that the falsity of their claim would mean that rain always produces dry grass. Something more subtle is being said and something more subtle is then in turn being denied, and these subtle affirmations and denials don't straightforwardly translate into the affirmations and denials of classical propositional logic.
Or going back to my earlier post and putting it in simpler terms, we can deny a conditional with a simple denial of the metaphysical relation, or else with a counter-conditional, or else with a counterexample. When classical propositional logic denies a conditional it is limited to doing so with a counterexample (e.g. N ^ ~S). This is something of a bug, for to deny the essence of a conditional is to deny its conditionality (e.g. "N does not ensure S"). English is capable of all three responses; propositional logic is only capable of one.
*I am changing the proposition to avoid confusing double-negatives. -
 bongo fury
1.8k
bongo fury
1.8k
Yes, the red and white system at least. Unfortunate that it shades in where I was shading out. But it shows how logic uses "not" as a reversal of shading, sending anything in row 2 to row 4 (and vice versa, and also reversing shading within row 3). Whereas ordinary language, while it might do that, might equally well signal a retreat to the very top, leaving all options on the table.
Or (@Leontiskos) it might do something else more elaborate which deserves analysis. Rabbit holes galore, of course. :grin: -
 Leontiskos
5.6kI am starting to think that it is because the word "implies" has the idea of causality in it, while logic says nothing about causality. I reckon that it is better to think of a truth table as coexistence rather than causation. — Lionino
Leontiskos
5.6kI am starting to think that it is because the word "implies" has the idea of causality in it, while logic says nothing about causality. I reckon that it is better to think of a truth table as coexistence rather than causation. — Lionino
So I think you are overstating this idea. Conditionals have a directionality that partially mimics causality. Meta-logically, they are intended to support the inferences of modus ponens and modus tollens. These are directional, asymmetric inferences. When you think in terms of coexistence or when @bongo fury speaks about "Not A without B" or Venn diagrams, you both seem to be thinking primarily in symmetric, non-directional terms. For example, "coexistence" is not asymmetrical or directional like (A→B). It is symmetrical like (A^B).
Further, "A implies B" does not necessarily mean that A causes B. As I said on the first page, the relation can be indicative. For example, the antecedent can be a sign of the cause that is the consequent. "Warmth implies fire," does not mean that warmth causes fire. "Implies" can also be correlative, where two correlates are caused by a third thing, but this is a true case of coexistence, in which the relation is biconditional (and therefore symmetric) rather than merely conditional (and therefore asymmetric).
There are lots of legitimate ways to speak about (A→B) in English, and each is incomplete:
- Forms relating to ¬¬(A→B):
- "Not(A without B)"
- "Not A without B"
- "No A without B"
- "¬A and/or B"
- Forms relating to modus ponens:
- "If A then B"
- "A implies B"
- "B follows from A"
- "B from A"
- Forms relating to modus tollens:
- "If ¬B then ¬A"
- "¬B implies ¬A"
- "¬A follows from ¬B"
- "No ¬B without ¬A"
- "Without B, no A"
- (I omit the forms relating to the idiosyncrasies of material implication)
There are also lots of legitimate ways to speak about ¬(A→B) in English, and each is incomplete:
- Forms relating to (A^¬B):
- "A without B"
- "A but not B"
- "A and not B"
- Forms relating to the denial of modus ponens:
- "Not(If A then B)"
- "A does not imply B"
- "B does not follow from A"
- "No B from A"
- Forms relating to the denial of modus tollens:
- "Not(If ¬B then ¬A)"
- "¬B does not imply ¬A"
- "¬A does not follow from ¬B"
- "¬B without ¬A"
- "B requires no A"
- (I omit the forms relating to the idiosyncrasies of material implication)
Of course some of these overlap. For example, the multiple meanings of "without" make "Not A without B" ambiguous between a directional modus ponens and a non-directional ¬A∨B.
Again, "No one transformation is more central to [the logical] 'meaning' than any other" (). Privileged meanings only emerge at the meta-logical level:
On the other hand, in English, or most European languages, nobody ever says "X implies false/true", that comes off as gibberish. The reason must be because the word 'implies' has the sense of (meta)physical causation, while logical implication is not (meta)physical causation; the latter starts with the antecedent being true, the former may have a false antecedent. — Lionino
- If it rains, then the grass will be wet.
- If Hitler was a military genius, then I'm a monkey's uncle.
These are equivalent at the first-order level, but not at the meta-logical level. At the first-order level they are both true and there is no difference between the truth of (1) and the truth of (2). At the meta-logical level, (1) partakes in the true purpose of a conditional whereas (2) does not (link). (2) is a consequence of the idiosyncrasies of the material conditional. This relates to my earlier point that the logical negation of a conditional is no longer a conditional, and in that case the modus ponens and modus tollens are no longer accessible, and because of this the directionality of the conditional dissipates.
If one does not make the meta-logical distinction between (1) and (2) then they will be tempted to claim that conditional logic cannot map asymmetrical or directional relations (including causation). This isn't right. A conditional can map an asymmetrical relation. Can it map something like causality? Yes and no: partially but not fully, because causation is not entirely truth-functional.
The key here is that propositional logic distinguishes (1) from (2) not in themselves, but extrinsically through modus ponens and modus tollens. Even though (2) is 'true', nevertheless it cannot be used to draw any substantial conclusion. Calling the conditional "true" is just a useful fiction which has no practical impact on the system. Or rather, it shouldn't. In the other thread we are seeing the havoc that meta-logical ignorance can wreak, for to permit standing contradictions gives the "dross" of the material conditional a potency it was never intended to have. It turns the useful fiction into non-fiction. - Forms relating to ¬¬(A→B):
-
 Leontiskos
5.6kOf course some of these overlap. For example, the multiple meanings of "without" make "Not A without B" ambiguous between a directional modus ponens and a non-directional ¬A∨B. — Leontiskos
Leontiskos
5.6kOf course some of these overlap. For example, the multiple meanings of "without" make "Not A without B" ambiguous between a directional modus ponens and a non-directional ¬A∨B. — Leontiskos
I suppose it is worth asking whether these are the same two inferences, and whether the first is any more "directional" than the second:
- (A→B)
- A
- ∴ B
- ¬A∨B
- A
- ∴ B
I want to say that they are different mental inferences, which is why we think of them differently (in English). But this is part of the difficulty of the thread. "Rabbit holes." -
 TonesInDeepFreeze
3.8kThey are different.
TonesInDeepFreeze
3.8kThey are different.
One is an inference of B from {A -> B, A}.
The other is an inference of B from {~A v B, A}
However, A -> B and ~A v B are equivalent, so the inferences are different but equivalent.
As to "directional", we'd need a definition of "directional".
What "rabbit hole" there is depends on the silly rabbit looking for real or imagined rabbit holes. -
 Lionino
2.7kif A is false then we can say A→B, and yet your English does not capture this move. — Leontiskos
Lionino
2.7kif A is false then we can say A→B, and yet your English does not capture this move. — Leontiskos
But it does. If we understand A→B as «not A without B», and we have ¬A, it is within the scenarios that «not A without B» precludes, because it only precludes A, ¬B, it doesn't preclude ¬A ever.
While ¬(A→B) tells us exactly «A without B», as it is the same as A&¬B. -
 Leontiskos
5.6kBut it does. If we understand A→B as «not A without B», and we have ¬A, it is within the scenarios that «not A without B» precludes, because it only precludes A, ¬B, it doesn't preclude ¬A ever. — Lionino
Leontiskos
5.6kBut it does. If we understand A→B as «not A without B», and we have ¬A, it is within the scenarios that «not A without B» precludes, because it only precludes A, ¬B, it doesn't preclude ¬A ever. — Lionino
I think you may have mixed up a bit of the verbiage there, but I think you are saying that «not A without B» prescinds from whether or not ¬A justifies the conditional, and that is precisely my point. «not A without B» does not capture the fact that ¬A makes the conditional to be automatically true.
Or in other words, I can say, "¬A, therefore A→B," and clearly «not A without B» does not justify such a move. If all we knew about A→B was «not A without B», then we would not know that such a move is valid. -
 Lionino
2.7kNot A without B means you can't have A without having B. Everything else is allowed. That everything else includes ¬A.
Lionino
2.7kNot A without B means you can't have A without having B. Everything else is allowed. That everything else includes ¬A. -
 Lionino
2.7k¬A ⊢ A→B — Leontiskos
Lionino
2.7k¬A ⊢ A→B — Leontiskos
If we read this as "¬A being true means A→B is true", it looks fine to me. I wouldn't read it as «¬A entails A→B», as 'entail' is a synonym of 'imply', and (English) A being false tells us nothing about whether it implies something.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Logical positivism was right, with respect to an ideal logical language.
- Can unproven or hard to debunk logical chain create or support religion?
- The differences/similarities between analytic, a priori, logical necessity, and absolute certainty
- Possible revival of logical positivism via simulated universe theory.
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum