-
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
You can certainly argue for nihilism from robust deflation, but the position that it is obvious or widely accepted that validity and logical consequence "have nothing to do with truth," is belied by a look at any introductory text on logic.
You could refer to the open source ForAllX (which is very much focused on formalism), but which still defines consequence in its opening pages thus:
"For the conclusion to be a consequence of the Ppremises, the truth of the premises must guarantee the truth of the conclusion. If there is a counterexample, the truth of the premises does not guarantee the truth of the conclusion."
Or you could look at a more advanced text like the Routledge Philosophical Logic, which distinguishes between "truth simpliciter" and a "relativized notion of truth: truth in a model," and how the latter was historically developed from as a means of capturing the former.
Notions of truth outside formalism are called on all the time though. For instance, this highly cited piece by Priest (one of the major figures on dialtheism) on paradoxes of material implication.
The notion of validity that comes out of the orthodox account is a strangely perverse one according to which any rule whose conclusion is a logical truth Is valid and, conversely, any rule whose premises contain a contradiction is valid. By a process that does not fall far short of indoctrination most logicians have now had their sensibilities dulled to these glaring anomalies. However, this is possible only because logicians have also forgotten that logic isa normative subject: it is supposed to provide an account of correct reasoning. When seen in this light the full force of these absurdities can be appreciated. Anyone who actually reasoned from an arbitrary premise to, e.g., the infinity of prime numbers, would not last long in an undergraduate mathematics course.
-
 frank
18.7k
frank
18.7k -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
Read what? Obviously I can't read the sources I just quoted since they disagree with you.
I mean, on your view that "virtually all logicians embrace deflationary theories of truth," don't you think it is a little strange that:
A. They largely responded to a survey rejecting that position and;
B. That the most used introductory text book for logic in the English speaking world begins by discussing validity in terms of true conclusions or relating formalism to states of affairs on its opening pages, with nary a single mention of deflation in the whole text? -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
The opening lines of the SEP article on logical pluralism acknowledge that the idea seems crazy at first glance, but that it becomes more plausible on further examination. I found myself getting more of a handle on it when reading the objections to it. It's all pretty technical, and that's not really something I'm super familiar with, but I did get that logical pluralism isn't taking anything away from the regular logic.
Neither of the two most cited arguments for pluralism, Beale and Restall or Shapiro argue that trivial logics should be considered correct.
Beale and Restall only endorse a few sub-classical logics and Shapiro based his "eclectic pluralism" on use cases in mathematics.
Pluralism is not the position that all logics are correct. It is the position that more than one is.
The position that any logic is correct is more in line with nihilism, although the nihilist will simply reject the idea of a correct logic. -
 Leontiskos
5.6k
Leontiskos
5.6k
Good posts. I would still say that until someone proffers logical pluralism, it will just be a moving target. When we talk about "logical pluralism" we are apparently talking about something that no one on TPF holds. And if someone on TPF wants to say that they hold and defend "logical pluralism," then they are the one who needs to tell us what the hell they mean by it, lol. Until that happens the wheels will continue to spin without any traction. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
I don't think it's that hard to define at all. Some posters in this thread seemed to pick it up intuitively. Aside from B&R's book, they have shorter articles, and this question has been answered succinctly in many places. Their argument is roughly that the intuitive/informal notion of logical consequence is multiply-realizable (granted it is more technical in its details).
I find this version of pluralism quite plausible. The most obvious example of ambiguity in natural language is propositions about the future, which, given some (fairly popular) assumptions, are indeterminate, rather than true or false. And this is one that has a long pedigree, being discussed since antiquity (arguably being endorsed by Aristotle from the very outset on the readings of many commentators).
One could also argue that the intuitive/informal notion of logical consequence is irrelevant. I think that's a tough argument to make, but it's a possible one. What is bizarre to me is claiming that this must be the case and that anyone who disagrees has utterly failed to understand what the topic and logic as a whole.
The best way of summarising the difference between monism, pluralism, and nihilism is as follows:
Monism: there is only one true logic.
Pluralism: there are at least two true logics.
Nihilism: there are no true logics.
Whether one is a monist, pluralist, or nihilist will depend a lot on what one takes a logic to be about and whether logics have to satisfy certain properties, like being universal, normative (capturing "rules of good thought"), and so on. Certain kinds of nihilism have a lot in common with certain kinds of pluralism (Aaron Cotnoir's nihilism is very close to a view of pluralism called logic-as-modelling, for example).
This is a typical response, but based on some takes in this thread typical answers to this question are all way out in left field.
Active academic philosophers and logicians have been surveyed on this BTW:
https://survey2020.philpeople.org/survey/results/4858?aos=37
As Chalmers notes in the paper on this, "pluralism" was the most popular write in option so this overstates the commitment to classical logic, but not entirely. -
 Moliere
6.5kI think thinking in terms of "laws" is probably unhelpful here and I have never seen a monist argument that tries to define itself in this way. If by laws we mean "true for all existing logics," then there are clearly no such laws. The monist doesn't argue that such laws "hold in generality," except insofar as they hold for "correct logic" (as they variously define it; note also that most monists embrace many logics, the question is more about consequence). So, Russell's paper is fine overall, but I think this part has just confused people because it's easy to read it in a way that seems to make the answer trivial. But based on the fact that even pluralists themselves very often claim that they are in the minority, it should give us pause if monism seems very obviously false. — Count Timothy von Icarus
Moliere
6.5kI think thinking in terms of "laws" is probably unhelpful here and I have never seen a monist argument that tries to define itself in this way. If by laws we mean "true for all existing logics," then there are clearly no such laws. The monist doesn't argue that such laws "hold in generality," except insofar as they hold for "correct logic" (as they variously define it; note also that most monists embrace many logics, the question is more about consequence). So, Russell's paper is fine overall, but I think this part has just confused people because it's easy to read it in a way that seems to make the answer trivial. But based on the fact that even pluralists themselves very often claim that they are in the minority, it should give us pause if monism seems very obviously false. — Count Timothy von Icarus
I'm fine with another rendition other than "laws" -- that's just usually the word that comes up. I don't think they are literal laws though, not even in the "laws of nature" sense.
I ought say that I don't think monism is obviously false. I'd say monism is kind of the "default" position when we start logic, if there is a default position at all -- strictly speaking it seems to me that monism/pluralism/nihilism are more philosophies about logic than logic proper. It seems when we're doing strictly logic it wouldn't matter for the purposes of pursing the logic whether there are one or many logics (or consequence relations, as you put it). But the impression that logic gives with its generality seems to indicate there would not be another set of logical rules that lead to different consequences -- that would violate the law of non-contradiction.
I'm thinking this (very consistent!) holding onto the LNC is a part of why these developments have taken so long to be achieved.
I think part of the confusion is that, just as idealism is much more popular on TPF than in metaphysics as a discipline, highly deflationary conceptions of logic's subject matter are also much more common. But one might agree to a deflation of truth for the purposes of doing logic without embracing any robust notion of deflation, e.g. that "on 9/11 the Pentagon was struck by an airliner not a cruise missile," is true or false in a sense transcending any formal construct or social practice. Maybe not, I only know of two surveys on this question, but they do seem to bear this out, as does the way authors actually talk about non-classical logics (i.e. they spend a lot of time making plausibility arguments, which are superfluous of logic is just about formalism). — Count Timothy von Icarus
Oh, certainly*. For my part I think the metaphysics of truth ought to be set to the side for purposes of the question -- I'd say if our metaphysics of truth can't accommodate our logic then it's our metaphysics that are in error. Hence the motivation to develop a logic sans-metaphysics, insofar that it's possible. It seems to me that acknowledging the implications of a logic without commitment is about as close as we can get there. I agree with the part of your quote here:
*EDIT: Certainly, the positions on TPF are a niche that's not representative of the academic community. And though I respect and even rely upon the academy I'm pretty sure my philosophical sympathies are not exactly academic.
Ontologically, the pluralist is going to be the one who thinks that objective/external reality is chaotic or random enough to support all sorts of anomalies and fluxes with respect to the relations between its constituent facts. (Logical nihilism, or rather logical asemanticism, seems more accurate in this context, though, if it is not accurate to think that reality is structured according to any completely specifiable system of logic at all. Or maybe there are a few rules that are universal as such, i.e. exactly those pertaining to universal quantification, if this be doable in an unrestricted way.)
I've mentioned the absurd as my metaphysical stance to kind of hint at why this is interesting to me -- I take the absurd as something of a starting point now-a-days. Reality at least seems chaotic and random enough to support a multiplicity of necessities that disagree.
So, no, my stance is not metaphysically innocent at all. In some ways Priest was appealing because he laid out a more coherent way of talking about these absurdities that seem real but are difficult to put into philosophical words.
I'm very much avoiding basing logic on either science or natural language reasoning even though I think natural language reasoning -- or informal reasoning -- is the origin of formal logic.
It seems to me logic is a bit like math (while not being reducible to math) in the way that it can be developed or "discovered".
My background epistemology of "guess and check", very much inspired by my understanding of science, definitely feeds into my motivation for a pluralistic philosophy of logic -- but I'm trying to avoid claiming either the mantle of science or the common sense of natural language reasoning in making my point. Which is probably why it falls flat. -
 Banno
30.2k@Count Timothy von Icarus
Banno
30.2k@Count Timothy von Icarus
Providing links or references to sources and quotes, and linking mentions, are basic courtesies.
https://www.reddit.com/r/askphilosophy/comments/1ggtpw0/what_is_a_correct_logic_re_monismpluralismnihilism/
https://philosophy.stackexchange.com/questions/118553/what-is-a-correct-logic-re-the-logical-monism-pluralism-nihilism-debate -
 Banno
30.2kWhat should stand out in this discussion is that if there is one true logic, one true consequence relation. or definition of "correct logic", or a logic that can pares all arguments made in a natural language and allow us to determine their validity, or whatever monism is chosen, then it ought be possible to set it out.
Banno
30.2kWhat should stand out in this discussion is that if there is one true logic, one true consequence relation. or definition of "correct logic", or a logic that can pares all arguments made in a natural language and allow us to determine their validity, or whatever monism is chosen, then it ought be possible to set it out.
But that has not been done.
So it remains that logical monism is an act of faith rather than a conclusion.
The discussion of monism, pluralism and even nihilism is ongoing, not settled. -
 Banno
30.2k↪@Leontiskos ↪Banno To what extent does your disagreement on this involve, perhaps, one being a conservative and the other liberal? — Tom Storm
Banno
30.2k↪@Leontiskos ↪Banno To what extent does your disagreement on this involve, perhaps, one being a conservative and the other liberal? — Tom Storm
A curiosity I came across in the Philpapers survey. The analysis examines correlations with other questions, most of which are to do with anti-realism and contradictions and such, where the correlations seem related. But then there was this:

There is a correlation between philosophers who reject abortion and accept only classical logic. What to make of that? -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
Well I should note that the quotations I shared are from some other places as well, I was collating them because I discovered that (almost) the same question had been answered several times before.
But as far as I can tell, they are all generally saying the same thing (feel free to search for "logical pluralism" though), which jives with my understanding of the question.
So it remains that logical monism is an act of faith rather than a conclusion.
But the view that there are multiple correct logics or none wouldn't require act of faith? -
 Banno
30.2kBut the view that there are multiple correct logics or none wouldn't require act of faith? — Count Timothy von Icarus
Banno
30.2kBut the view that there are multiple correct logics or none wouldn't require act of faith? — Count Timothy von Icarus
Not at all.
Despite being accused of engaging in a "polemic" by , I continue to think the issue both interesting and open:
Now it seems to me that Pluralism is the better of these options, but the devil is in the detail, and the discussion is on-going. — Banno
Do you think that the discussion is closed? -
 Tom Storm
10.7kThere is a correlation between philosophers who reject abortion and accept only classical logic. What to make of that? — Banno
Tom Storm
10.7kThere is a correlation between philosophers who reject abortion and accept only classical logic. What to make of that? — Banno
That is interesting.
Is there a correlation (from what you have seen) between those philosophers who privilege the classical tradition (ancient Greeks) and conservative politics? -
 Banno
30.2kGood question. I don't see a question in the survey that addressed this.
Banno
30.2kGood question. I don't see a question in the survey that addressed this.
After a bit more searching, there was also this:

Philosophers who reject god seem more willing to reject classical logic. Not unexpected, perhaps. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
There is a lot of interesting stuff in there, and I really wish they had it on a platform that made it easier to slice and dice the data, because you could also look at the correlations by specialty area and I think that's almost as interesting.
The one trend I find amusing is that as one goes further back in time for historical specialties philosophers get less and less confident that "philosophy makes progress."
It would be interesting to do a similar survey of amateur philosophy spaces and compare. Idealism, epistemic nihilism, and anti-realism for instance are much more popular here it seems.
I would expect some big variance on key philosophers:
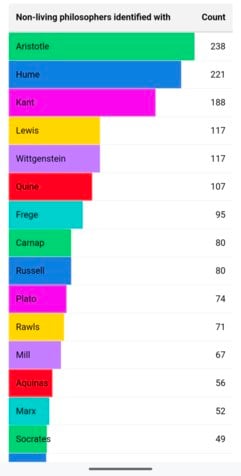
Aristotle and Kant make sense for people who go into academia. I imagine Nietzsche would be vastly more popular writ large. Judging from what bookstores carry he is by far and away the most popular. -
 TonesInDeepFreeze
3.8kMy statements are in context of ordinary symbolic logic. Things may be different depending on alterative logics:
TonesInDeepFreeze
3.8kMy statements are in context of ordinary symbolic logic. Things may be different depending on alterative logics:
Isn't a tautology as much a contradiction as anything? (p or ~p) — Cheshire
No. A tautology is a formula that is satisfied by every interpretation. No contradiction is satisfied by any interpretation. Therefore, no tautology is a contradiction.
And
P v ~P
is not a contradiction.
Godel concluded that no system really has a foundation — Cheshire
What specific remarks by Godel are you referring to?
if we follow the evidence it suggest that self-reference isn't a reliable source of truth, in the sense the system breaks down per Russell and Godel. — Cheshire
From Godel-Rosser we have certain systems that have self-reference and are (if consistent) incomplete. What do you mean by "break down"?
/
I've always wondered if Russell's paradox is coming from the foundations of set theory: the contradiction of fencing in infinity. — frank
The paradox pertains to any 2-place relation, not just the 'member of' relation.
Irrespective of set theory:
For any 2-place relation R, there is no x such that x bears R to y if and only if y does not bear R to y.
/
I don't recall the post, but in this thread (or another?) someone mentioned LEM in relation to the liar paradox. We don't need to refer to LEM for the liar's paradox. The contradiction is obtained even without LEM.
We don't need to argue this way:
L -> ~L
~L -> L
L v ~L
therefore L & ~L ... contradiction
Rather we can argue this way:
L -> ~L
so ~L
~L -> L
so L
therefore L & ~L ... contradiction
Or, intuitionistically:
L -> ~L
so ~L
~L -> L
so ~~L
therefore ~L & ~~L ... contradiction -
 Banno
30.2kReference?
Banno
30.2kReference?
Yes, I'd enjoy being able to interrogate the data, although the sample size is a bit small.
A similar survey could be done here using SurveyMonkey or some other. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
It's way at the bottom of the demographics.
https://survey2020.philpeople.org/survey/results/demographics -
 Moliere
6.5kI don't recall the post, but in this thread (or another?) someone mentioned LEM in relation to the liar paradox. We don't need to refer to LEM for the liar's paradox. The contradiction is obtained even without LEM. — TonesInDeepFreeze
Moliere
6.5kI don't recall the post, but in this thread (or another?) someone mentioned LEM in relation to the liar paradox. We don't need to refer to LEM for the liar's paradox. The contradiction is obtained even without LEM. — TonesInDeepFreeze
While others may have done so, in this thread that's been me aping Priest.
The idea is to point out a difference between LNC and LEM, as well as to prove that thedialeithicdialethic answer to the liar's is still valid in the sense of using some classical logical laws. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Of course LNC and LEM are different.
I can't find the post about the liar paradox; my own point was merely the technical one that the contradiction of the liar does not require LEM. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k -
 Cheshire
1.1k
Cheshire
1.1k
None. I thought that was the result of his numbering system for mathematical proofs. The Godel numbers, lead to a conclusion that you can't in fact provide support for every mathematical assertion. Without reaching some paradox. I don't remember the details.What specific remarks by Godel are you referring to? — TonesInDeepFreeze
Fair point. Trying to see if I could argue it. Boolean logic is pretty solid.No. A tautology is a formula that is satisfied by every interpretation. No contradiction is satisfied by any interpretation. Therefore, no tautology is a contradiction. — TonesInDeepFreeze -
 TonesInDeepFreeze
3.8klead to a conclusion that you can't in fact provide support for every mathematical assertion. Without reaching some paradox. — Cheshire
TonesInDeepFreeze
3.8klead to a conclusion that you can't in fact provide support for every mathematical assertion. Without reaching some paradox. — Cheshire
"provide support for" is vague in supposedly explaining the vague "has no foundation"
The main branches of classical mathematics are formalizable in set theory. However, if set theory is consistent then there are statements in the language of set theory such that neither the statement nor its negation is a theorem of set theory. Moreover, if set theory is consistent then set theory does not prove the consistency of set theory. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
It's interesting that the proof of "if set theory is consistent then set theory does not prove that set theory is consistent" is not so much analogous to the logic of the liar or barber paradox but rather to a different paradox, viz. Curry's paradox aka 'the Santa Claus paradox'. -
 Moliere
6.5kOf course LNC and LEM are different. — TonesInDeepFreeze
Moliere
6.5kOf course LNC and LEM are different. — TonesInDeepFreeze
Heh. Well, I'd expect that from you :D -- I'm not sure that the differences between them are at the level of "of course" for the participants here.
I can't find the post about the liar paradox; my own point was merely the technical one that the contradiction of the liar does not require LEM.
I agree. I don't think the liar's needs anything technical at all. For thems who prefer utterances we can frame it in plain language as "I am telling a falsehood right now" -
 Leontiskos
5.6kI don't think it's that hard to define at all. — Count Timothy von Icarus
Leontiskos
5.6kI don't think it's that hard to define at all. — Count Timothy von Icarus
I haven't seen anyone define any of the positions in a clear and non-vacuous way, much less go on to argue in favor of one or another.
Their argument is roughly that the intuitive/informal notion of logical consequence is multiply-realizable (granted it is more technical in its details). — Count Timothy von Icarus
"There are multiple formal ways of realizing the informal notion of logical consequence." I suppose this gives us something, but I don't think it is very substantial. If, for example, everyone agrees that Aristotelian syllogistic and propositional logic are two ways of formalizing the informal notion of logical consequence, then where does the actual disagreement lie?
Again, what is needed is someone who believes they disagree and is willing to set out a substantial argument. The polemicists disagree without substance, and the rest of us are not sure what we are supposed to be disagreeing about. -
 Moliere
6.5kI haven't seen anyone define any of the positions in a clear and non-vacuous way, much less go on to argue in favor of one or another. — Leontiskos
Moliere
6.5kI haven't seen anyone define any of the positions in a clear and non-vacuous way, much less go on to argue in favor of one or another. — Leontiskos
If dialethism is true then pluralism is true.
Dialethism is true as it resolves the liar's paradox in a clear, non-vacuous way.
Therefore, pluralism is true.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum








