-
 TonesInDeepFreeze
3.8k"An argument is deductively valid if and only if it is not possible for the premises to be true and the conclusion false." (The Logic Book - Bergmann, Moor and Nelson).
TonesInDeepFreeze
3.8k"An argument is deductively valid if and only if it is not possible for the premises to be true and the conclusion false." (The Logic Book - Bergmann, Moor and Nelson). -
 TonesInDeepFreeze
3.8kSo then any argument that has no true premises is valid. That's weird. — frank
TonesInDeepFreeze
3.8kSo then any argument that has no true premises is valid. That's weird. — frank
No, that's not correct.
If there is no assignment in which all the premises are true, then the argument is valid.
That is very different from what you mentioned. -
 Leontiskos
5.6kThere is no question. He does not presuppose it. — TonesInDeepFreeze
Leontiskos
5.6kThere is no question. He does not presuppose it. — TonesInDeepFreeze
There is no question that he would reject your tendentious interpretation, which fully ignores the bolded sentence of Gensler's.
Suppose you are on the jury. @Hanover presents his defense. It is a garbled mess of incoherent and contradictory gibberish. He concludes, "...Therefore, the defendant is innocent." The jury goes into deliberation. You say, "Well, we must first recognize that Hanover's defense was a piece of valid reasoning." The rest of the jury looks at you with blank stares. You continue, "His premises were inconsistent, and any argument with inconsistent premises is necessarily valid." The blank stares only become more protracted.
Now it would not help you in any way if Gensler and Enderton were fellow jurors. Even more than the other jurors, they would think you were confused. Gensler might say, "Did you read past the first sentence of my explanation of validity? Very few people would construe it in the bizarre way you have, but even so, I went on to clarify the concept in the following sentences."
I did not claim that validity requires that there is no interpretation in which the premises are all true. — TonesInDeepFreeze
And I never said you did (you are falling into the fallacy of affirming the consequent). You think that any argument with inconsistent premises is automatically valid, not that every valid argument has inconsistent premises. Here is Gensler:
We’re just saying that the conclusion follows from the premises – that if the premises were all true, then the conclusion also would have to be true. — Gensler, Introduction to Logic, Second Edition, p. 3
Validity has to do with the conclusion following from the premises. Your claim is, "Whenever the premises are inconsistent, the argument is valid." But inconsistent premises do not show that the conclusion follows from them. Hanover's defense is not valid reasoning just because it is confused.
(Now you can hold to your tendentious position if you like, but it is not the position of Gensler, or Enderton, or SEP, or Wikipedia.) -
 Leontiskos
5.6kOh. So then any argument that has no true premises is valid. That's weird. — frank
Leontiskos
5.6kOh. So then any argument that has no true premises is valid. That's weird. — frank
Any argument with inconsistent premises is valid, according to Tones. Weird indeed. It requires a strained reading of the fine print of portions of definitions of validity, taken out of context. Earlier posters usefully leveraged the word "sophistry."
(Note that this is different from the modus ponens reading of the OP and it is different from the explosion reading of the OP. The effect of explosion requires explicit argumentation. The OP, for example, is susceptible to explosion, but it is not wielding explosion. Tones is just doing a weird, tendentious, definitional thing.) -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
I ignored nothing. The bolded part is another way of saying the unbolded part:
"An argument is valid if it would be contradictory (impossible) to have the premises all true and conclusion false. In calling an argument valid, we aren’t saying whether the premises are true. We’re just saying that the conclusion follows from the premises – that if the premises were all true, then the conclusion also would have to be true."
So, flip the bolding:
"An argument is valid if it would be contradictory (impossible) to have the premises all true and conclusion false. In calling an argument valid, we aren’t saying whether the premises are true. We’re just saying that the conclusion follows from the premises – that if the premises were all true, then the conclusion also would have to be true."
They are two ways of saying the same thing. And:
Gensler:
"An argument is valid if it would be contradictory (impossible) to have the premises all true and conclusion false."
It is impossible to have both A -> ~A and A true. Perforce, it is impossible to have the premises all true and the conclusion false. — TonesInDeepFreeze
Which you ignored.
And you ignored these:
"A sentence Phi is a consequence of a set of sentences Gamma if and only if threre are no interpretations in which all the sentences in Gamma are true and Phi is false." (Elementary Logic - Mates)
"An argument is deductively valid if and only if it is not possible for the premises to be true and the conclusion false." (The Logic Book - Bergmann, Moor and Nelson).
With bolding for your bolding pleasure:
"A sentence Phi is a consequence of a set of sentences Gamma if and only if threre are no interpretations in which all the sentences in Gamma are true and Phi is false." (Elementary Logic - Mates)
"An argument is deductively valid if and only if it is not possible for the premises to be true and the conclusion false." (The Logic Book - Bergmann, Moor and Nelson).
/
You've mentioned a hypothetical trial. I don't claim that the formal notion is suitable in all situations.
My point has never been that the formal notion should have dominion over all contexts. Rather, it has been shown that the original argument is valid per ordinary formal logic.
I did not claim that validity requires that there is no interpretation in which the premises are all true.
— TonesInDeepFreeze
And I never said you did (you are falling into the fallacy of affirming the consequent). — Leontiskos
I affirmed no consequent. To be clear, I said I did not say the thing, whether you said that I said it or not.
Meanwhile, I did not say that the inference is "trivial" though you've twice now claimed I did.
Your claim is, "Whenever the premises are inconsistent, the argument is valid." — Leontiskos
That is the second time you put quotes around words I didn't say. The fifth time in this thread you've put words in my mouth.
"If the premises are inconsistent, then the argument is valid" is equivalent with my wording of the definition, but for the purpose of the definition, I don't mix consistency (syntactical) with satisfiabilty (semantical). So you are incorrect when you put those words in quotes and ascribe them to me. -
 Leontiskos
5.6kThat is the second time you put quotes around words I didn't say. — TonesInDeepFreeze
Leontiskos
5.6kThat is the second time you put quotes around words I didn't say. — TonesInDeepFreeze
It's called paraphrase, and we both know you hold to the paraphrased proposition. You should be a lawyer given the way you constantly complain, nitpick, and manage bizarre readings interpreted via a form of legalese.
"A sentence Phi is a consequence of a set of sentences Gamma if and only if threre are no interpretations in which all the sentences in Gamma are true and Phi is false." (Elementary Logic - Mates)
"An argument is deductively valid if and only if it is not possible for the premises to be true and the conclusion false." (The Logic Book - Bergmann, Moor and Nelson). — TonesInDeepFreeze
These are not conclusive in favor of your reading, and you would need to quote the context around these sentences given the way you have shown yourself willing to ignore context.
"It is not possible for the premises to be true and the conclusion false" is not uncontroversially fulfilled by a set of inconsistent premises. You are literally interpreting English conditionality via the idiosyncrasies of the material conditional, which is ironic given the way you protest labels which reduce your thinking to truth-functional categories. It is curious to me that you do not recognize the way your argument rests on a mere technicality.
I'm really not convinced this is going anywhere given how many times you have now repeated yourself, but the issue here has to do with consequence or inference vs. the material conditional. I gave examples of sources which agree that a valid argument requires that the conclusion follows from the premises, and everyone knows that the idiosyncratic/trivial case of the material conditional, where a false antecedent automatically makes the conditional true, is not a case of "follows from." This is why logicians refused to admit the material conditional for many decades after Frege had attempted to introduce it.
"Hanover's defense was logically inconsistent, therefore his conclusion follows from his defense," is not correct. B does not automatically follow from A whenever A is incoherent. -
 TonesInDeepFreeze
3.8kAnother one:
TonesInDeepFreeze
3.8kAnother one:
"a major topic in the study of deductive logic is validity. This is a
relationship between a set of sentences and another sentence; this relationship holds whenever it
is logically impossible for there to be a situation in which all the sentences in the first set are true
and the other sentence false." [bold added]
https://logiclx.humnet.ucla.edu/Logic/Documents/CORE/LogicText%20Chap%200%20Aug%202013.pdf
From that same source:
"An "argument", in its technical sense, consists of two parts: a set of sentences, called the premises, and a sentence called the conclusion. The term "argument" may suggest a dispute, but in logic something is called an argument whether or not any people ever have or ever will disagree about it. Likewise, the "premises" of such an argument may or may not have been believed or asserted by somebody, and it is sometimes useful to examine arguments whose "premises" would never be believed by any rational person. Likewise, by calling something a "conclusion" we do not suggest that anyone ever has or even should "conclude" this thing on the basis of the premises given." -
 Leontiskos
5.6k"a major topic in the study of deductive logic is validity. This is a relationship..." — TonesInDeepFreeze
Leontiskos
5.6k"a major topic in the study of deductive logic is validity. This is a relationship..." — TonesInDeepFreeze
The idea that it is a relationship already excludes your reading. If a relationship between A and B must be established, then one must know something about both A and B. Yet you think that merely knowing something about A—that it is inconsistent—proves validity. If an isolated fact about A proved validity then validity would not be a relationship between A (premises) and B (conclusion). This is another source that excludes your view. The other (single-sentence) sources you presented favor my view but do not exclude your tendentious view. -
 TonesInDeepFreeze
3.8kIt's called paraphrase — Leontiskos
TonesInDeepFreeze
3.8kIt's called paraphrase — Leontiskos
In this instance, the use of quote marks made it look like a quote, and not just a paraphrase.
And even as a paraphrase, it would be incorrect.
These are not conclusive in favor of your reading, and you would need to quote the context around these sentences given the way you have shown yourself willing to ignore context. — Leontiskos
Oh, please. (1) I do not ignore context. (2) They are simple definitions. (3) How much context would I have to type for you? (4) The cites you gave are equivalent with my wording and the wording of the two recent cites I gave.
A reasonable person would see those quotes and say, "Okay, I do see that your definition is used too and that yours and the others are equivalent." Instead, you can't stand to concede even the simplest point.
"it is not possible for the premises to be true and the conclusion false" is not uncontroversially fulfilled by a set of inconsistent premises. — Leontiskos
It's not at all controversial in ordinary formal logic. It is easy to see that if a set of sentences is inconsistent then there is no interpretation in which all the members are true.
And look at your own cites:
"An argument is valid if it would be contradictory (impossible) to have the premises all true and conclusion false. In calling an argument valid, we aren’t saying whether the premises are true. We’re just saying that the conclusion follows from the premises – that if the premises were all true, then the conclusion also would have to be true." [bold added]
"In logic, specifically in deductive reasoning, an argument is valid if and only if it takes a form that makes it impossible for the premises to be true and the conclusion nevertheless to be false. It is not required for a valid argument to have premises that are actually true, but to have premises that, if they were true, would guarantee the truth of the argument's conclusion." [bold added]
It's remarkable that you can't stand to be wrong - to the degree that you don't heed even your own cites!
/
"it is impossible that all the premises are true and the conclusion is false"
"it would be contradictory (impossible) to have the premises all true and conclusion false"
"there are no interpretations in which all the sentences in Gamma are true and Phi is false"
"impossible for there to be a situation in which all the sentences in the first set are true
and the other sentence false."
"not possible for the premises to be true and the conclusion false"
"there is no interpretation in which the premises are all true and the conclusion is false"
Those are all ways of saying the same thing.
But you can't recognize that which is blazingly clear. -
 Banno
30.2kIt's remarkable that you can't stand to be wrong to the degree that you don't heed even your own cites! — TonesInDeepFreeze
Banno
30.2kIt's remarkable that you can't stand to be wrong to the degree that you don't heed even your own cites! — TonesInDeepFreeze
The level of dishonesty here is extraordinary. -
 TonesInDeepFreeze
3.8kThe idea that it is a relationship already excludes your reading. If a relationship between A and B must be established, then one must know something about both A and B. — Leontiskos
TonesInDeepFreeze
3.8kThe idea that it is a relationship already excludes your reading. If a relationship between A and B must be established, then one must know something about both A and B. — Leontiskos
The validity relation is:
{<X Y> | X is a set of sentences & Y is a sentence & there is no interpretation in which all the members of X are true and Y is false}
So, easily we have that an argument is valid if and only if it is a member of that relation.
The validity relation is a relation in the ordinary formal sense of a set of ordered pairs. That is distinct from any of the ordered pairs themself. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Thanks for that post. It is helpful and I need to look more into the subject. -
 Benkei
8.1kNo I think you did understand me and we are disagreeing. I find the discussion interesting and I see where people are coming from concluding the argument is valid. If I approach it formalistic I would say: normal modus ponens, fine, valid, because I don't care what it says.
Benkei
8.1kNo I think you did understand me and we are disagreeing. I find the discussion interesting and I see where people are coming from concluding the argument is valid. If I approach it formalistic I would say: normal modus ponens, fine, valid, because I don't care what it says.
However, the reductio shows that the first premise is unsound but why is it unsound? It's unsound because it's logically contradictory. If A then not-A necessarily implies A and not-A, which tells me the argument must be invalid. -
 frank
18.7kIf there is no assignment in which all the premises are true, then the argument is valid.
frank
18.7kIf there is no assignment in which all the premises are true, then the argument is valid.
That is very different from what you mentioned. — TonesInDeepFreeze
Yes, I understand. -
 frank
18.7kAny argument with inconsistent premises is valid, according to Tones — Leontiskos
frank
18.7kAny argument with inconsistent premises is valid, according to Tones — Leontiskos
Inconsistent? If you look at the argument in the OP, there can never be a case where both premises are true. According to the definition of validity in the SEP article on propositional logic, the argument in the OP is valid. It's odd at first glance. -
 Banno
30.2k
Banno
30.2k
Yep.If you look at the argument in the OP, there can never be a case where both premises are true. — frank
Any argument with inconsistent premises is valid, according to Tones — Leontiskos
Compare (A & ~A) → B. Of course Tones is right, because anything follows from such a contradiction.
Leon has no idea. -
 Michael
16.6kHowever, the reductio shows that the first premise is unsound but why is it unsound? It's unsound because it's logically contradictory. If A then not-A necessarily implies A and not-A, which tells me the argument must be invalid. — Benkei
Michael
16.6kHowever, the reductio shows that the first premise is unsound but why is it unsound? It's unsound because it's logically contradictory. If A then not-A necessarily implies A and not-A, which tells me the argument must be invalid. — Benkei
1. "Sound" in this context means "the premises are true and the conclusion follows". It doesn't make sense to say that premises are sound or unsound; it is arguments that are sound or unsound.
2. "Valid" in this context means "if the premises are true then the conclusion follows". An argument can be valid even if one or more of its premises are false (and even if one or more of its premises are necessarily false).
3. A → ¬A does not mean A ∧ ¬A. It means ¬A ∨ ¬A. The argument in the OP is equivalent to:
¬A ∨ ¬A
A
∴ ¬A
To offer a more meaningful example:
I am not 36 years old or I am not 36 years old
I am 36 years old
Therefore, I am not 36 years old
It's possible for the first premise to be true (it's true if I am not 36 years old) and it's possible for the second premise to be true (it's true if I am 36 years old), but it's not possible for both premises to be true.
The argument is an example of the principle of explosion; from a contradiction anything follows. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
Just to note: tautology is semantic and contradiction is syntactic.
Sure, tautologies might be semantic, e.g. "bachelor's are unmarried men," or "triangles are three-sided." Yet aren't these really just expressing that the two terms are actually the same term, i.e. A = A, something taken to be true by virtue of its form?
Anyhow, it seems like we also have cases the formula itself is always true, regardless of which valuation is used for the propositional variables. Wouldn't these be tautologies?
For example:
(p→q) ⇔ (~q→~p) (contraposition)
Or:
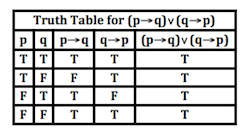
Or, in the context of this thread A→~A and ~A or ~A
At least in propositional logic, my understanding is that tautologies are defined in terms of form, hence Wittgenstein's claim that the propositions provable in logic are all in some sense tautological. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
See: "implications are disjunctions."
https://discrete.openmathbooks.org/dmoi3/sec_propositional.html#:~:text=Implications%20are%20Disjunctions.&text=P%20%E2%86%92%20Q%20is%20logically%20equivalent%20to%20%C2%AC%20P%20%E2%88%A8%20Q%20.&text=Example%3A%20%E2%80%9CIf%20a%20number%20is,else)%20it%20is%20even.%E2%80%9D
This plus De Morgan's Laws end up being important because we can do transformations into disjunctive normal form, which is easy for computers to check. -
 Moliere
6.5kWhen I say A sarcastically, I mean ~A, of course. And that is equivalent with A -> ~A. But I don't present it like that at all. I just say A and there is an implicit premise that when I say it, I mean its negation. I don't know how even modal logic could capture that. Or maybe, I am saying that A is true in an alternative world and false in the actual world, but even that seems far-flung.
Moliere
6.5kWhen I say A sarcastically, I mean ~A, of course. And that is equivalent with A -> ~A. But I don't present it like that at all. I just say A and there is an implicit premise that when I say it, I mean its negation. I don't know how even modal logic could capture that. Or maybe, I am saying that A is true in an alternative world and false in the actual world, but even that seems far-flung.
Getting back to Srap Tasmaner, he's looking for a use of A -> ~A in everyday discourse. I don't think your proposal works, since people don't acutually say things of the form A -> ~A to convey sarcasm. It seems to me that you followed an interesting idea, but it doesn't do the job here. — TonesInDeepFreeze
Fair enough. I agree it doesn't fit the form -- people don't actually say the implication, it's only equivalent to the implication (but so are so many other formulas...). -
 Michael
16.6kThese mean the same thing:
Michael
16.6kThese mean the same thing:
1. P → Q
2. ¬Q → ¬P
These do not mean the same thing:
1. P → Q
3. P → (P ∧ Q)
The misunderstanding is that many here are misinterpreting (1) as (3). "if ... then ..." in propositional logic does not mean what it means in ordinary English. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
I haven't given it much thought but I am pretty sure this holds for strict implication as well.
If: "if p is true then q is necessarily true (true in all possible worlds)" then if follows that we cannot have both not-q and p. So, I guess the xor.
And my guess is that this would be true in other attempts to capture relevance vis-á-vis entailment too, since it intuitively makes sense.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum








