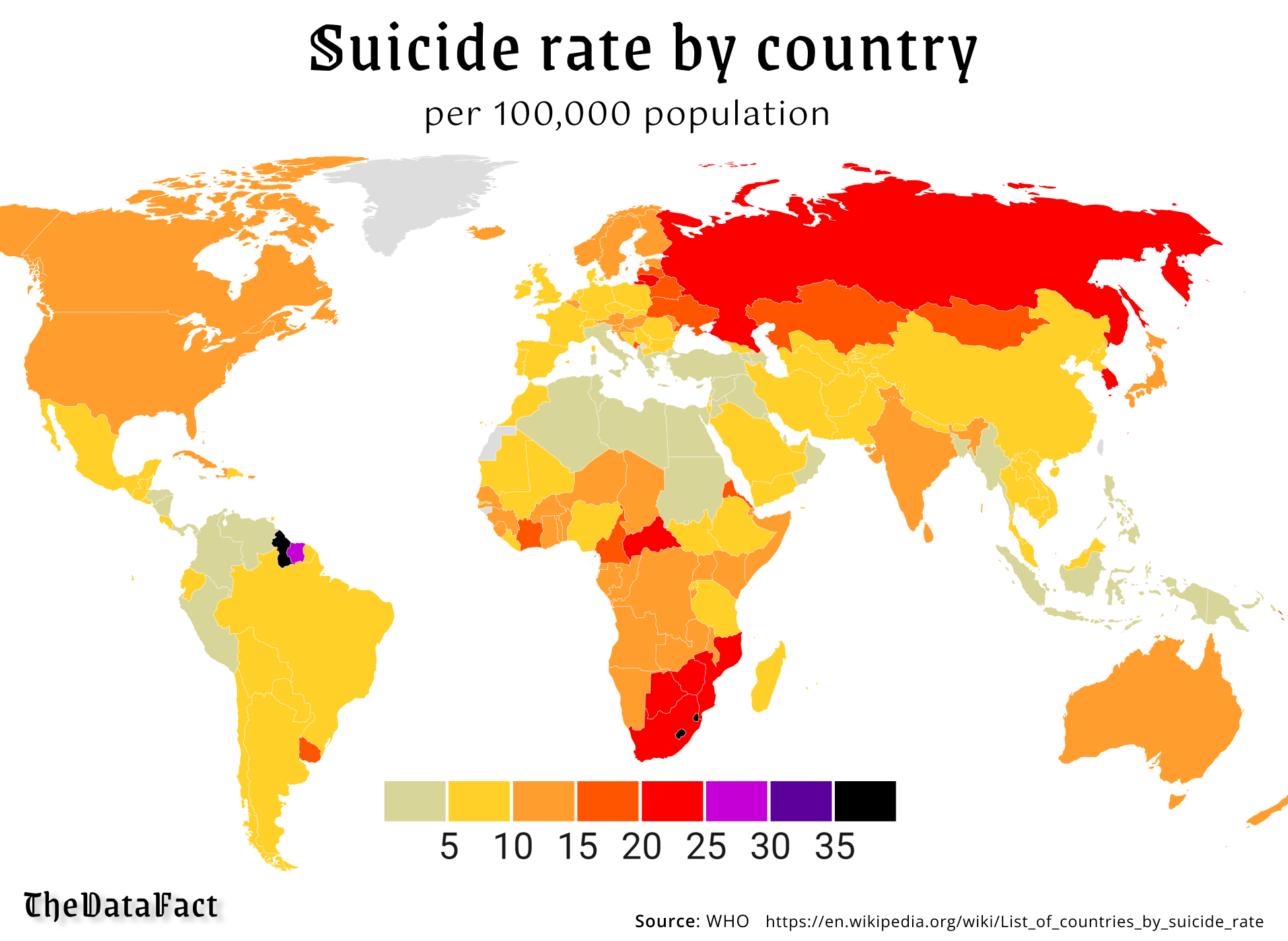
As a fun fact, we could determine the coffee mug is hotter than its environment by cutting the mug diametrically and taking the average speed of the particles of each infinitesimal dx vertical line from one end of the diameter to the other end, which is exactly the temperature gradient.



If there is a gradient peaking at the center and bottoming on the corners, the mug is sending heat to its environment. If the gradient peaks on the corner, the mug was taken from the fridge.

The temperature of an ideal gas and the speed of its particles i=1, 2, …, N with mass m is had in:

$U = \sum_{i=1}^{N}\frac{mv_{i}^{2}}{2}=\frac{3nRT}{2}$

But the evidence says probably only with Homo sapiens about 100,000 years ago. — apokrisis

Not necessarily. Neanderthals had language, and they split from us 500k years ago.

The problem in the ethical theories created by many self-regarded saints is that they end up in the logical conclusion that we should kill a person (or ourselves) to harvest organs to save many others. That however does not align with our moral intuition, so it is safe to discard the theory.

My opinion is that even coming up with a normative ethical theory is already missing the point of what ethics is supposed to be.

Am I wrong for prioritizing my kid? — RogueAI

No. Out-group preference is quite literally an evolutionary «death end».

What kind of odds would you give to the climate being that way? — RogueAI

100%. As soon as I say a few factories make no difference here and there you will just move goalpost and say that doesn't qualify as "enough small changes". Your weasel word there is "enough", it can mean anything from cow farming all the way to nuclear warfare.

I am still not gonna eat the bugs, I will use AC, I will drive a car.

It would be funny if it weren't sadly hypocritical how the moderators are willing to let their chihuahua bark and attack others but will censor anyone who gives the 36 year old bachelor a taste of his own sour medicine.

Is there a manlet alliance behind the curtains on this website? If you want to say there isn't, start moderating both ways, not just one way. There is no third option here.

He got his mod powers removed for a reason, and this is not about politics.

If "red" is just in your mind, when you ask for a red pen, how is it that the person you are asking hands you what you want? — Banno

A regularity between a cause and the perception it creates between two different people. It is at least the case with colour-blind people, who will often still give you the right pen, even though we know they don't see the same as we do, as the shade of brown of red is a bit different than the shade of brown of green.

Without Y, what can be said of X? How do you know it exists and what are its properties? — Hanover

Mary's room?

We don't say: If Gu{P} |- Q and Gu{P} |- ~Q, then ~P |- G. — TonesInDeepFreeze

I made a mistake. I meant to say:

"The bulk of the debate here between Banno and Leontiskos (and me interjecting sometimes) is why say G |- ~P instead of P |- ~G."

That is something that Banno expresses here:

Indeed, the "problem" is not with reduction, but with and-elimination. And-elimination has this form
ρ^μ ⊢ρ, or ρ^μ ⊢μ. We can choose which inference to use, but both are quite valid.

We can write RAA as inferring an and-sentence, a conjunct:

ρ,μ ⊢φ^~φ⊢ (ρ→~μ) ^ (μ→~ρ)

(ρ^μ) →φ^~φ⊢ (ρ→~μ) ^ (μ→~ρ)
(fixed error)

...and see that the choice is not in the reductio but in choosing between the conjuncts. — Banno

It has happened before in the history of science where we had to reject G when finding out that Gu{P} is contradictory, because P was so evidently true.

Ugh. — TonesInDeepFreeze

You got it wrong. I know what I meant with my posts. "We" there refers to me, I was not talking about anyone else. The specific post you quoted did not help sort out the issue, specifically the nitpick on "translation", which is why I had to make a whole new thread for that topic specifically. In fact in my thread you corrected yourself about something midway through the discussion:

I'm dumping this: — TonesInDeepFreeze

But feel free to take credit for whatever you want in your mind, it doesn't bother me.

Sobre ciertas palabras, y también la semántica, he escrito este breve parágrafo:

La palabra "slur" originalmente significaba difuminar u ofender. Ahora, como sustantivo, significa “una palabra ofensiva que se usa para insultar a alguien por su raza, sexualidad, vel cetera”. En español no existe traducción de este concepto, porque en la hispanosfera una división de los insultos en función de lo que se ataca se considera arbitraria (con una excepción), y no es merecida. El “slur” existe de manera religiosa, que la raza o la sexualidad son estados moralmente protegidos. Asimismo, en español existe la blasfemia, una especie de insulto contra Dios, que es precisamente de carácter religioso. Inventaron así una nueva categoría de insultos, basada en algo que no se debe hablar ni pronunciar porque resulta ofensivo; pero esta categoría no existe para la mayoría, ya que no se prohíben las palabras basadas en sentimientos. Está prohibido por razones religiosas, de ahí la blasfemia — el "slur" es un concepto religioso.

I see now. — Lionino

@Count Timothy von Icarus
I still would like some final thoughts on this post specifically.

You're welcome for that. (Not too very bumptious of me.) — TonesInDeepFreeze

The post you quoted there was before you joined these threads. So there is no connection to you. "We" there simply means "I" — not bumptious of me, the greatly humble person I am.

1. (S & ~P) -> (B & ~B) {1}
2. S {2}
3. ~P {3}
4. B & ~B {1,2,3}
5. ~~P {1,2} — TonesInDeepFreeze

Ok, that is the derivation. The source I quoted at least is correct when abriding it. The RAA however is not how it was being presented in this thread by others before, which is what I was trying to confirm.

With the non-intuitionistic form we can have the sentence on the last line be P. — TonesInDeepFreeze

We are all speaking non-intuitionistically here, which is standard at least in amateur circles.

(1) If Gu{P} |- Q and Gu{P} |- ~Q, then G |- ~P — TonesInDeepFreeze

The bulk of the debate here between Banno and Leontiskos (and me interjecting sometimes) is why say G |- ~P instead ~P |- G.
The debate gets to the point on this post https://thephilosophyforum.com/discussion/comment/918628 by me
then to this https://thephilosophyforum.com/discussion/comment/918657 by Leontiskos
then this https://thephilosophyforum.com/discussion/comment/918724 by me
then he replied with this https://thephilosophyforum.com/discussion/comment/919282 and this post right under https://thephilosophyforum.com/discussion/comment/919292
I did not further reply

I ask that you check those before replying on this specific point, as I don't want to go in circles or pointlessly extend the thread.

the husband is a simp if he doesn't go to the football match without her; in the long run, the wife will respect him more for ignoring her ultimatums rather than giving in — 180 Proof

God bless. The "game theory" of anything-relationship must keep in mind that male and female psychology are wildly different. Women don't like, respect, or feel attraction towards push-overs. It is just another instantiation of the "nice guys finish last" universal.

This makes zero sense to you. — Treatid

No, I am informing you that your string of words makes zero sense. It perhaps "makes sense" to you in the same way that 12+12=22 made to me in my early childhood.

And that Logical language has a set of axioms that need a set of axioms that need a set of axioms. — Treatid

That is not how it works. A language is not a theory. The axioms of language, in this case n-order logic, are not the same as the axioms of a mathematical theory. And the axiom tree/chain does not keep going forever.

If I wanted to release the kraken, I would tag Tones and he would inundate this thread with corrections on your posts. I am using my posts to inform you that you don't really understand what it is that you are saying. It is up to you to insist in mistakes or not.

I don't care what you believe in, you are a completely confused person too deep in your own dogmatic fantasies. As someone else said "You write slop".

You said "The main threat to good healthcare is the lack of religion.". That is false. Depression and suicide attempts have no strong global correlation with religiosity.

Technically: it is impossible to define axiomatic mathematics and first order logic. We haven't actually proved they don't exist - just that we cannot say anything meaningful about them. — Treatid

This makes zero sense.

As such, for any given set of axioms we need a set of axioms that uniquely defines how to interpret that set of axioms. — Treatid

Those "sets of axioms" are the logical language chosen.

For all practical purposes, we can treat them as if they don't exist. The distinction between "can't be described" and "don't exist" is moot. — Treatid

Also makes zero sense.

This would be impossible if the contradictory theory was erected on a logical foundation containing the Boolean principle Ex Contradictione Quodlibet ECQ, from a contradiction everything follows. So ECQ has to be abandoned, but fortunetely that proves possible, indeed mathematically straightforward. What remains is a rich field, of novel mathematical applications interesting in their own right, which sidestep the vexing questions of which foundational principles to adopt, by developing contradictions in areas of mathematics such as number theory or analysis which are far from foundations. — SEP's Inconsistent Mathematics

In a parallel with the above remarks on rehabilitating logicism, Meyer argued that these arithmetical theories provide the basis for a revived Hilbert Program. Hilbert’s program was the project of rigorously formalising mathematics and proving its consistency by simple finitary/inductive procedures. It was widely held to have been seriously damaged by Gödel’s Second Incompleteness Theorem, according to which the consistency of arithmetic was unprovable within arithmetic itself. But a consequence of Meyer’s construction was that within his arithmetic R# it was demonstrable by finitary means that whatever contradictions there might happen to be, they could not adversely affect any numerical calculations. Hence Hilbert’s goal of conclusively demonstrating that mathematics is trouble-free proves largely achievable as long as inconsistency-tolerant logics are used.

The arithmetical models used by Meyer and Mortensen later proved to allow inconsistent representation of the truth predicate. They also permit representation of structures beyond natural number arithmetic, such as rings and fields, including their order properties. Axiomatisations were also provided. — SEP's Inconsistent Mathematics

It should be emphasised again that these structures do not in any way challenge or repudiate existing mathematics, but rather extend our conception of what is mathematically possible. This, in turn, sharpens the issue of Mathematical Pluralism; — SEP's Inconsistent Mathematics

Various authors have different versions of mathematical pluralism, but it is something along the lines that incompatible mathematical theories can be equally true. The case for mathematical pluralism rests on the observation that there are different mathematical “universes” in which different, indeed incompatible, mathematical theorems or laws hold. Well-known examples are the incompatibility between classical mathematics and intuitionist mathematics, and the incompatibility between ZF-like universes of sets respectively with, and without, the Axiom of Choice. It seems absurd to say that ZF with Choice is true mathematics and ZF without Choice is false mathematics, if they are both legitimate examples of mathematically well-behaved theories. — SEP's Inconsistent Mathematics

Shapiro’s distinctive position has other ingredients: mathematics as the science of structure, and mathematical pluralism implying logical pluralism (on logical pluralism see also Beall and Restall 2006); but we do not take these up here. — SEP's Inconsistent Mathematics

The primacy of theories fits, too, with the natural observation that the epistemology of mathematics is deductive proof. It is only if one takes as a starting point the primacy of the mathematical object as the truth-maker of theories, that one has to worry about how their objects manage to co-exist. — SEP's Inconsistent Mathematics

Saying nonsense again, aren't we?

We have made a full lap on this conversation, going over to something that has been discussed already. I ask that anyone, if forgetting, go back to the beginning of this page to remember what arguments were given. I am not going to reply anymore to anyone who is simply repeating what has already been said.

I think we've gotten beyond this talk of "objects". We've moved on to "rules", because rules are what formalism takes for granted. — Metaphysician Undercover

It has already been discussed that rules may be considered objects.

formalism takes rules for granted — Metaphysician Undercover

"Taking something for granted" means nothing in this context.

These seem very similar to me, though you seem to have a desire to drive a wedge between platonism and formalism. — Metaphysician Undercover

That is just projection from you. I am correctly stating these two are distinct views, one may be a formalist without being a platonist and vice-versa.

If rules are supposed to exist in the same way that platonic objects are supposed to exist, then there is no real difference between the two. — Metaphysician Undercover

That is just going back to square one but talking about rules instead of numbers, see my first line in this post.

inclines me to think — Metaphysician Undercover

Idc.

Then the rules simply "are", just like platonic objects simply "are", and formalism is a form of platonism. — Metaphysician Undercover

If you had a single reference to support this nonsensical claim, you would have given it already. You talk about "rules" without specifying what kind of rule you are talking about. If it is a mathematical rule, see the first line in this post and then this post.

Trying encoding the cases where the statements are false:
A→(B∧¬C), ¬A→((¬B∧C)∨(¬A∧C)), B→((A∧¬C)∨(¬A∧C)), ¬B→((A∧¬B)∨(C∧¬B)), C→(¬B), ¬C→((A∧¬C)∨(¬A)∨(¬C)) (not informative), (A∧¬B)∨(¬A∧B)∨(A∧¬C)∨(¬A∧C)∨(B∧¬C)∨(¬B∧C) does not entail C
Tried it with if and only if instead
A↔(B∧¬C), ¬A↔((¬B∧C)∨(¬A∧C)), B↔((A∧¬C)∨(¬A∧C)), ¬B↔((A∧¬B)∨(C∧¬B)), C↔(¬B), ¬C↔((A∧¬C)∨(¬A)∨(¬C)), (A∧¬B)∨(¬A∧B)∨(A∧¬C)∨(¬A∧C)∨(B∧¬C)∨(¬B∧C) does not entail C

Replacing my post above with if and only if does not work either.

I tried Claudius 3.5, nothing useful came out.

ChatGPT 3.5 after some back and forth gave me:
T(A)→T(B), T(B)→Z(B), T(B)→¬T(B), T(C)→L(B), ∀x(T(x)→¬L(x)∧¬Z(x)), ∀x(L(x)→¬T(x)∧¬Z(x)), ∀x(Z(x)→¬T(x)∧¬L(x)), ∃x(T(x)∧∀y(T(y)→y=x)), ∃x(L(x)∧∀y(L(y)→y=x)), ∃x(Z(x)∧∀y(Z(y)→y=x)), but it does not entail T(C).

Is it possible to formulate it using first-order logic? — javi2541997

I gave another try, without using a third-value (ie classical first-order logic).

I used A→(B∧¬C), B→((A∧¬C)∨(¬A∧C)), C→(¬B), (A∧¬B)∨(¬A∧B)∨(A∧¬C)∨(¬A∧C)∨(B∧¬C)∨(¬B∧C)
Where :

• A→(B∧¬C) is if A, B tells the truth and C lies
• (B→((A∧¬C)∨(¬A∧C))) is if B, {A tells the truth and C lies} or {A lies and C tells the truth}
• C→(¬B) is if C, B lies
• (A∧¬B)∨(¬A∧B)∨(A∧¬C)∨(¬A∧C)∨(B∧¬C)∨(¬B∧C) are the conditions that one of the three has to lie and another tell the truth

Unfortunately, all that does not entail C, which is the right answer. I wonder why.

So I have no idea how Macedonia was more civilized. — Athena

They were not more civilised, the OP is categorically baloney — it shouldn't even need to be argued. Alexander himself was a huge lover of Persian culture, perhaps putting it higher even than his own Greek culture. He himself engaged in Persian customs at times.

You mean Aufklärung?

It is no mystery that we may build whatever system possible by tweaking the axioms and logical language we use for it. So why is it a surprise that there is some perceived "arbitrariness" to mathematics and logic when put under this light? Mod-60 arithmetic has been useless for us for most of history, and yet now our society relies fully on clocks. Putting mathematics in a heavenly pedestal is something I used to do.

If the so-called mathematical objects are fictions then they are not really objects, but fictions. — Metaphysician Undercover

And to call them objects would be false by the principles of that ontology. — Metaphysician Undercover

The fictionalist position is that mathematical truths are fictional (that was already explained further by me above), and, since they are nominalists, that there is no such thing as abstract objects. That is the position, engaging in a debate about "object this object that" is pointless as you will choose to tailor the meaning of "object" to suit your ends.

then we need some other ontology to support the reality of rules — Metaphysician Undercover

Ok. Psychologism, I choose you!

Then the reality of agreement, convention, needs to be accounted for, and pragmaticism is designed for this purpose. — Metaphysician Undercover

Ok, am I supposed to disagree? Formalism is still not disguised platonism, much less nominalism.

I don't require your courtesy. — TonesInDeepFreeze

So the conversation is over. I cannot take seriously someone who pretends to be a bully while simultaneously coming off as senile.

Or we read different news.

You don't have to feel they are needed nor do you have to request them for me to state them. — TonesInDeepFreeze

But you should observe those requests or needs before people's courtesy runs out.

Or maybe just say:

Laws of thought are the necessary mental conditions for the operation of the mind. — TonesInDeepFreeze

That is how I gave them some pages ago.

From that definition, it follows that they can't be broken. — TonesInDeepFreeze

Correct. We had this same conversation before.

So, when a person is utterly irrational, they are still obeying the laws of thought on account of the fact that there are mental conditions necessary for the operation of their mind? — TonesInDeepFreeze

Correct. Especially if by irrational you mean things of the sort of believing the colour green is sweet and that the moon is made of cheese.

If a mystic experiences contradictions as being true, then he's not breaking the laws of thought? — TonesInDeepFreeze

I don't think any such experiences are possible.

If one dreams that one's great-grandfather is both alive and dead at the same time, one is not breaking the laws of thought? — TonesInDeepFreeze

I don't think that is possible either.

But, if it is the case that it is possible, definitionally there are no laws of thought that preclude from that happening, because it happened, therefore oen is not breaking laws of thought.

He doesn't. — TonesInDeepFreeze

The public assessment of my skills in logic wasn't needed or requested.

And a fact about minds is that they are often irrational. — TonesInDeepFreeze

>completely ignores the actual definition right under that mere opening

"People operate mentally in all kinds of ways: Fictionally, absurdly, poetically, ironically, day dreaming, dreaming, mystically and insanely." is not a rebuttal anymore than it misses the point of the word 'operation'.

A law of thought is necessary for the mind no matter what it is doing, ironising, dreaming, thinking, or whatever. All of these have subjacent operations that are necessary to them.

I would wish you did.

Laws of thought are facts of the matter about your mind — Lionino

Let's understand instead 'laws of thought' as the necessary conditions/operations for my/human/any mind. Since they are necessary, they cannot be broken. — Lionino

In any case, the discussion around grammar is finished for me. If anyone wants to carry on, the following prerequesites are in place:

• knowledge of morphology at least at secondary-school level;
• knowledge of syntax at least at secondary-school level;
• knowledge of phonetics/phonology;
• knowledge of three or more languages at least at B2 level;
• at least surface knowledge of one classical language.

And by secondary I mean actual secondary, not Anglo-American high school. Scots does not qualify as a separate language from English, neither does Jamaican. Thanks.

You're replies don't even come close to a refutation. — TonesInDeepFreeze

Naturally the refuted wouldn't want to admit it.

In such mental states, people often break the laws of thought. — TonesInDeepFreeze

What laws of thought? You are not working under the definition that has been restated several times now.
In fact, how can someone violate a law of thought? Then it is not a law anymore but a suggestion or preference, innit?

Definition of what? — TonesInDeepFreeze

The definition that precludes people "breaking laws of thought all the time".

And before another circle comes about, the fact of tautology has already been recognised in another post.

It's plain as day — TonesInDeepFreeze

I am not gonna repeat the same thing until we circle all the way back to what was being talked about in the fifth page. I am not amnesiac.

That is not even remotely constant (2) In this instance, I've been in exactly the right place about what was posts was quoted. — TonesInDeepFreeze

It doesn't happen in this thread only. By the way, you forgot to add that "[emphasis added]" is an addition of yours to my post. Typically one would leave from making such an addition to the body of text and simply state before the quotation "bold is mine".

So that is saying that laws of logic may only allude to or be based on laws of thought. — TonesInDeepFreeze

Correct interpretation.

the laws of thought require — TonesInDeepFreeze

I didn't say anything like that. Laws of thought are facts of the matter about your mind, they don't require anything, they establish in what ways we are allowed to think in and not allowed to think in. If we are able to reject this or that principle, that principle is definitionally not a law of thought. If we are not able to reject a principle, perhaps that principle represents a law of thought.

Your objection to "If ___, then ___" is a doozy! — TonesInDeepFreeze

It was never an "objection" because it was never a reply to anything. It is indeed syntactically incorrect, and I pointed it out in a standalone post without referring to anyone. You butted in because you wanted to.

For disclosure, I didn't read that whole French article. I quoted it for the definition only.