Comments
-
Quality of education between universities?Depends on whether you are talking about undergraduate or graduate education. A question about the "quality of education" in general would make more sense for undergraduate education. For graduate education you would be more interested in specific departments that have a high standing in their field, and even specific professors with whom you would like to study.
As for undergraduate education, you'll hear a lot of platitudes, but don't underestimate such down-to-earth factors as the wealth of the institution. A well-off college will have more and better teachers, more teaching assistants, more and better facilities, including science labs. All this factors into the quality of education. -
Is time travel possible if the A theory of time is correct?You need presentism of course. Travel isn't possible at all in eternalism, given the usual A-definition of 'travel'. — noAxioms
What do you mean?
Thinking a bit more about this, if now is an objective fact on presentism, and the Time Traveler is transported some ways into the past or the future, what happens with the now? The situation is different from the normal "time travel" when everyone moves forward into the future in lockstep at 1 second per second, because the Traveler has left everyone else in the future (or the past). The only way this makes sense to me in the presentist framework is if now splits into two nows: one travels with the Traveler (where it entangles everyone else in his present) and one stays with his former contemporaries and continues on at its usual pace.
Note that these considerations are quite apart from the question of existence of the past and the future (which, frankly, make little sense to me). -
Is time travel possible if the A theory of time is correct?According to you, time doesn't pass at all, according to presentism. That can't be right. And I don't mean that in the sense that presentism can't be right, but in the sense that your construal of presentism can't be right.
-
Is time travel possible if the A theory of time is correct?The A theory holds that only the present time (and everything at that time) exists. Therefore any time other than the present time is not an available travel destination. This appears to rule out the possibility of time travel according to the A theory
However, there is one caveat, which is that the present time is always moving into the future.. — Luke
Exactly. So, presentism doesn't exclude all time travel. I don't see why presentism as such should be inimical to other kinds of time travel, proceeding at different rates than the normal forward rate. -
How does probability theory affect our ideas of determinism?Consider the following circular definition, which nevertheless has intuitive meaning. — sime
Determinism is the thesis that the state of the universe at any given time, together with the laws of nature, fixes (determines) the states of the universe at all other times. — SophistiCat
It's not circular, just because the word 'determines' occurs in the definition. You can easily rewrite the definition without that word.
But this definition is also fulfilled by taking determinism to refer only to the fixing of an arbitrary finite number of states. — sime
No, some is not the same as all, so your definition does not fit the above. I've never seen determinism used in this sense, so I don't see why this should be taken seriously. -
How does probability theory affect our ideas of determinism?It may fix an event with 50% probability from the perspective of a conscious observer, but still be determined by the universe itself. — Karl
No, I specifically said that it is fixed by "the state of the universe, together with the laws of nature" and contrasted that with what you are saying. The former would contradict determinism, the latter would not. -
How does probability theory affect our ideas of determinism?Say there is a 50/50 chance of some event occurring. How does that probability factor affect whether or not the universe is deterministic? — Josh Alfred
Determinism is the thesis that the state of the universe at any given time, together with the laws of nature, fixes (determines) the states of the universe at all other times.
Where does the 50/50 probability come from? If you are saying that the state of the universe, together with the laws of nature, fix some event with only 50% probability, then that directly contradicts the deterministic thesis. If you are saying anything other than that, e.g. that it is your subjective assessment of some outcome based on limited information, then it is irrelevant to determinism. -
Is logic undoubtable? What can we know for certain?The switch being on and off is an example of an inconsistent state of affairs. The SEP entry for States of Affairs gives the example of Paul's having squared the circle.
Also paraconsistent logicians accept or at least consider the existence of inconsistent physical objects. — Andrew M
See, we can say what it means for a sentence (for example) to be inconsistent. I don't think it is possible to say what it means for an object or a state of affairs to be inconsistent - without looping back to the language that we use to describe that object/state of affairs. So yes, you can sort of attribute inconsistency to things, but that attribution will be parasitic upon language, thought, reason. Of course, things and talk of things are hard to separate anyway, except that if we are realist to any extent, we accept that there is a one-to-many relationship between them. That is, there is one thing, but our relationship to it is through thinking/talking about it, and there can be more than one way to do the latter - including dialetheic ways.
Take the superposition state in quantum mechanics, for example. One way to talk about it is through the use of the quantum mechanical formalism, and there is nothing inconsistent about that - it's just straightforward linear algebra. But sometimes people feel that the mathematical formalism doesn't give us the feel, the intuitive understanding of what the thing is, and they try to accommodate it in more familiar, human-scale classical terms. Or they are actually committed to the view that, at least for macroscopic things like cats, such terms should always apply, quantum formalism be damned. One way or another, they can end up talking about the superposition state using a deliberately inconsistent model. Does it make the subject of their description itself inconsistent? Yes, as long as they are talking about it in that particular way, and with the understanding that the inconsistency awes itself to that particular conceptualization. -
Is logic undoubtable? What can we know for certain?What separates logic from opinion? (Hint validity) — Carmaris19
As @MindForged already told you, you are misusing the term "validity." A valid conclusion is a conclusion that is reached by following (some) rules of logic. Logic itself cannot be valid or invalid. -
What does 'scientifically impossible' mean?Scientific impossibility is logical impossibility in the following sense: If it is the case that I am sitting at a table, then it is logically impossible for it to be the case that I am not sitting at a table (within the same context where the first proposition is true). A scientific theory constrains the world to behave in certain ways, and not others. The logical corollary of that is that if you accept the theory (within some domain of application), then you cannot at the same time accept any proposition that (within the same domain of application) violates the constraints imposed by the theory, on pain of being logically inconsistent.
Now, that answers the narrow question. The closely related wider question is: What is the nature of scientific theories, or the laws of nature, as they traditionally have been called? How are we to make sense of the rules and constraints that they posit? That is a huge topic with a wide variety of views. -
Is logic undoubtable? What can we know for certain?Is it right that the idea is that the contradiction lies in what the person who drew the maps believes? That is, he believes both A and Not A. If so, I don't think the example really works. The content of my beliefs is contradictory, but there is still no actual state of affairs that is incoherent, is there? — PossibleAaran
Mental maps (and beliefs) are abstract representations of the world. We know that representations can be mistaken or inconsistent. But the maps are not the territory. — Andrew M
States if affairs or physical objects cannot be either coherent or incoherent. It is beliefs, mental maps, or what have you, that can have such a quality as coherency. -
Karl Popper and The Spherical EarthDoes the spherical Earth cast doubt upon Popper’s claims about scientific theories never been confirmed? — Craig
Confirmation is what happens when your confidence in a proposition or a theory increases in response to evidence. To deny that our confidence in the proposition that the Earth is round has ever changed, despite everything we have learned, is to deny reality.
Popper goes through ridiculous contortions to deny "confirmation," but in the end he is not actually saying anything different - he just says it more obscurely. -
At The Present TimeDo people say "time nowadays"? I googled the phrase, and although there are many hits, the sentence context is usually something like "...waste of time nowadays..." or "...time. Nowadays..."
-
What if spirituality is the natural philosophy?That’s a very aggressive stance you have there. I’m not an authority on his mental health, what’s the diagnosis? — AngryBear
Crackpottery is not a diagnosis - well, not necessarily - it is loopy pseudoscience in this case. Whether the guy really is off his rocker or whether he is just peddling this crap in a bid to make some money is really none of my concern. And I wasn't being aggressive - on the contrary, just wanted to give you some well-intentioned advice. When someone sees you citing a crackpot, they might think: "This person is not to be taken seriously. I better not waste my time listening to what he has to say." -
Kuhn, Feyerabend and Popper; Super Showdownconsidering the surge of popularity attributed to both Kuhn and Feyerabend (who where fierce anti-Popperians). I wouldn't say it's a banality. — Pelle
I didn't say all of Popper's ideas about science were banal - some of them were just wrong (kidding!) No, I was referring to ideas like "people trying to falsify eachother's theories" and other pop-Popperianisms that some people, including scientists, swear by. Popper's actual lasting impact on the philosophy of science is far more dubious than his rock-star fame would suggest. -
What if spirituality is the natural philosophy?Laird Scranton — AngryBear
He is a crackpot. You really don't want to bring this kind of crap into a philosophical discussion - it destroys all credibility. -
Nietzche and his influence on HitlerYes I understand Nietzsche is one of the hardest Philosphers to read and understand and congrats to all of you for you impeccable knowledge but some of you do come across as quite brash to someone who is just starting out. I am a mature student who has only recently been granted full use of her eyes over these last two years and I have a thirst for knowledge on the subject of Philosophy. I have chosen Nietzsche because I feel for what I have read so far that he is very misunderstood. — Helen G
Well, one thing Nietzsche is not is clear and consistent, which is why just about every scholar of Nietzsche thinks that he is misunderstood by someone (or even everyone) else. So, you are in a good company. -
Kuhn, Feyerabend and Popper; Super Showdownmodern science does follow Popper's ideas to some extent. The critical discussion around science today is exactly as Popper described: people trying to falsify eachother's theories. — Pelle
This is a banality.
The ideas that are popularly credited to Popper have been around since Bacon. What is right about Popper's prescriptions isn't new or radical at all. -
Is logic undoubtable? What can we know for certain?I would maintain that at least the law of non-contradiction is indubitable in just this sense: it cannot intelligibly be doubted. — PossibleAaran
Yes, even the law of non-contradiction can be intelligibly doubted: see Dialetheism
The a priori status of logic has been under attack for quite some time (as you can see above, even the sacrosanct non-contradiction is not safe). This is true even of the so-called "laws of thought," which is what you must really mean when you talk about logic, because formal or mathematical logic is as diverse and open-ended as mathematics. -
Another question about a syllogismWell, in this set up, we don't know anything about the relationship of odd and even, and we don't know anything about prime factorisations or that even means 'is divisible by 2 with no remainder'... The only premise here which is even related to even numbers and squares of even numbers is (1). — fdrake
Either you understand what is written, or you don't. If you don't, then nothing more can be said. If you do, then you know what "odd" and "even" mean. (But then if you do, you don't really need to go through this logical exercise in order to prove the conclusion - you could prove it by other means.)
I thought it was invalid because it seemed a lot like affirming the consequence to me. If you focus on the 2nd premise, — Ulrik
So the question becomes, can we conclude the statement: 'If the square of a number is even, then that number must be even' from the statement 'if a number is even, then its square must be even'? — fdrake
Why are you focusing on the second premise alone when two premises are given? -
Thought experiments and empiricismI don't know. It seems to me that only a defeasible statement can be meaningfully tested. How do you test a tautology (or a contradiction)?
I am familiar with this thought experiment, but not well-versed in its detailed treatment in the literature. I wonder how much of a point of contention this particular issue is. — Arkady
There seem to be quite a lot of references to the thought experiment in the literature - mostly it is (quite extensive) literature on thought experiments in general, but there are some specific examinations of Galileo's thought experiments, including some critical ones.
I found this paper interesting: D Atkinson, J Peijnenburg, Galileo and prior philosophy (2004)
They argue against the idea that Galileo succeeded in giving, in J. Brown's words, a "destructive" (against Aristotle's law of motion) and a "constructive" (in favor of Galileo's alternative) logical argument. Interestingly, they point to case where Aristotle happens to be right! It is the case of terminal velocity, which, under some conditions and idealizations, is directly proportional to the mass of the falling body. And yet Galileo would have it that this is logically impossible. How could that be?... -
Atheism is far older than ChristianitySomehow I feel I have been deprived of the epiphany I expected, reading the title. — Pair o'Ducks
Yeah, the title is odd: it's supposed to sound provocative, but how is what it ostensibly asserts even controversial?
The author's thesis is stronger than that: he argues that atheism was a "thing" in the ancient world, not just a few individual exemplars. -
Atheism is far older than ChristianityThe "study" is actually a book:
Tim Whitmarsh, Battling the Gods: Atheism in the Ancient World. New York: Alfred A. Knopf, 2015.
Here is the author's presentation: Battling the gods
And a (favorable) review from a classicist: Bryn Mawr Classical Review 2016.06.20 -
Question about a basic syllogismWhat I fail to understand however is that you can conclude 'Some Americans curse' from the premise 'All Americans curse'. You see, I thought if one says 'Some people are nice', one means that 'some people are nice, and some are not', rendering the deduction from 'All people are nice' impossible. — Ulrik
You are not wrong. Indeed, in natural speech, when we say "some A's are B," more often than not we mean that some are and some aren't. If we want to convey the other meaning, we might say something like "at least some A's are B." However, in the context of logic, in semi-formal syllogisms like the above, "some" is conventionally taken to express the latter meaning, that is
In set terminology: A ∩ B ≠ Ø (the intersection between all A's and all B's is not empty)
In predicate terminology: ∃x: Ax ∨ Bx (there exist subjects to which both predicates apply) -
Thought experiments and empiricismHere is a better (IMHO) refutation of Aristotle through thought experiment. Consider a dumbbell:
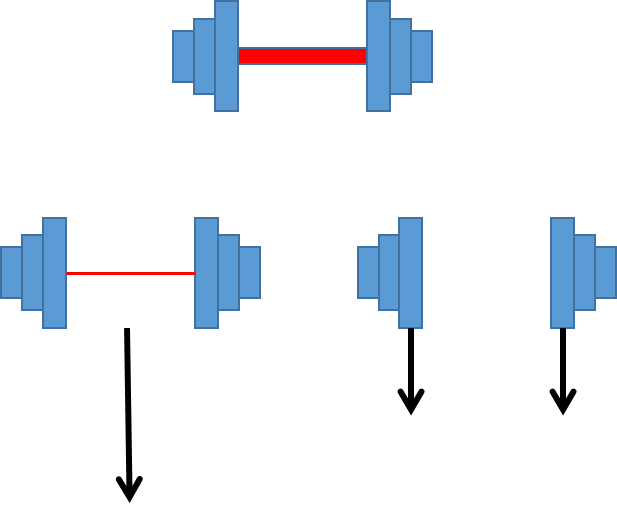
Let's take two such dumbbells. On one of them we will replace the connecting rod with a hair-thin wire, and on the other we will remove the rod altogether. Now let's drop these two "dumbbells" side by side. According to Aristotle, the two unconnected weights should drop with the same speed - so far so good. But the still connected dumbbell, simply by virtue of being individuated as one body with twice as much weight as either of the free weights, should drop much faster - twice as fast, if we take Aristotle's strongest formulation of his law*.
Unlike in Galileo's thought experiment, there is no logical reductio here. But the situation is physically implausible, because as long as the connecting wire is not stressed (and it need not be in this experiment), there is practically no difference between a "dumbbell" connected with a wire and a pair of identical unconnected weights.
* This is somewhat unfair to Aristotle, because in one of his more careful formulations, he says basically that ceteris paribus, the heavier body falls faster than the lighter. Here ceteris is most definitely not paribus. -
Thought experiments and empiricismI largely agree with your treatment of this question, Sophisticat. However, the above assumption (i.e. that the falling bodies behave as if they're separate bodies until the string is taut) seems debatable to me: as the weights were connected by the tether prior to their being dropped, they've always been "one body," and thus it could be argued that the composite body comprising the two weights plus tether would always fall faster than either body alone, given that they've always been one object for the purposes of this experiment. — Arkady
Aristotle, even as Galileo presents him in his dialogue, talks about "natural motion," which apparently is a free fall through some medium, such as air or water (neither Aristotle nor Galileo would contemplate vacuum). But in Galileo's setup, whenever the two bodies interact (the lighter body retards the motion of the heavier body), each body, when considered individually, is being acted upon by the other, and therefore is not in "natural motion." The entire system of two tethered bodies can (in Newtonian hindsight) be seen as one body in free fall, but neither one of the two bodies is in free fall when they interact.
So we can quibble over whether tethered bodies constitute one body, but the important thing is whether they constitute two independently falling bodies. If they don't, as Galileo's thought experiment requires, then Aristotle's law does not apply.
An interesting side note to all of this is that, if Aristotelian physics (or, at least the part of the theory which posits that heavier objects fall faster than light ones) really does imply a contradiction, one must reach the modal conclusion that there are no possible worlds in which heavier objects accelerate faster than light ones under the force of gravity alone! Intuitively speaking (for my intuition, anyway), it seems odd to put such a seemingly contingent physical fact on par with blatant contradictions such as square circles, or objects which are both red all over and green all over, etc. — Arkady
We don't even have to consider alternative physics, because Galileo gets the actual physics wrong. Bodies falling in a medium do not fall with the same speed. Now, Galileo surely realized this (as did Aristotle - he has a number of formulations of his law, some of which account for and even appeal to this fact), so he inserts a proviso that the bodies should be of the same material or the same specific weight. But this doesn't quite salvage his argument: a wood chip will fall slower than a log. And besides, this proviso does no work in the logic of his thought experiment, so it is irrelevant.
Galileo obtains the right result in a vacuum, in uniform gravity - thanks to the fact that gravitational mass is the same as inertial mass. But I don't see how this result can be obtained from a priori considerations. It was considered contingent enough for scientists in the 20th century to conduct sensitive experiments in order to test it. It is a generic consequence of Einstein's General Relativity, but that theory is not a priori either. -
Question about a basic syllogismNo decent people curse
Americans curse
Therefore
Some Americans are not decent — Ulrik
First, it is not entirely clear whether "Americans curse" means "Some Americans curse" or "All Americans curse." (Applying real-world knowledge, it seems more likely that they meant "Some Americans curse" - surely, there are Americans who don't curse?)
Fortunately, the conclusion "Some Americans are not decent" follows either way.
based on the premises it says 'all Americans are not-decent', not just 'Some Americans are not decent'. — Ulrik
But "all Americans are not-decent" implies "Some Americans are not decent," so the conclusion is still true. A valid argument does not have to have the most comprehensive conclusion possible. -
Thought experiments and empiricismIt seems you have missed the point entirely. According to Aristotle: — Inis
Right back at you. As I said right before the paragraph that you quoted, Aristotle (as per Galileo) does not treat of bound systems - his law concerns separate bodies. Galileo wants to stretch Aristotle's premises in a way that is, admittedly, physically intuitive, but strictly speaking, he cannot trap Aristotle in a contradiction by changing his premises. -
Thought experiments and empiricismSo, turning back to the OP for a change :)
If one had to choose a thought experiment to defend Norton's view, would Galileo's thought experiment that two falling bodies fall with the same acceleration be a suitable thought experiment since it can be empirically tested and it also can be written in a premise and conclusion argument form. I am not sure whether this would be a deductive argument though.
Also, wouldn't the assumption that connecting the heavier (H) and lighter ( L ) body makes one body of weight (H + L) mean that one of the premises of the argument would be false. — ADG
This refers to Galileo's famous argument against the then prevailing Aristotle's theory of falling bodies, according to which "bodies of different weight... move in one and the same medium with different speeds which stand to one another in the same ratio as the weights." While the apocryphal story says that Galileo conducted an actual experiment by dropping weights from the tower of Pisa, there is no evidence that he actually did this. All we have is a fictional dialogue between three characters. While one of the characters in the dialogue claims to have conducted an experiment of some sort, Galileo's stand-in declares that "without experiment, I am sure that the effect will happen as I tell you, because it must happen that way."
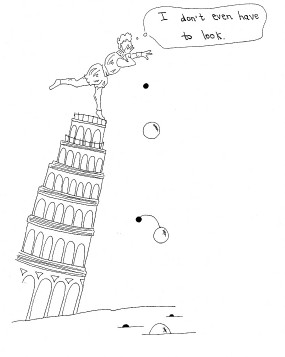
Galileo's argument is brilliant in its simplicity: Take two bodies of different weight connected by a string and drop them together. According to Aristotle, the lighter body will tend to fall slower than the heavier body, retarding its motion. Therefore, the two bodies together will fall slower than the heavier of the two would have fallen alone. But the combined weight of the tied bodies is greater than the weight of either of them, so again, according to Aristotle, the two should be falling faster. A contradiction.
However, as is often the case with thought experiments, this proof can be challenged. Galileo's reductio works by treating the two bound bodies as separate bodies in one part of the proof and as one combined body in another. But is it a legitimate move? Aristotle doesn't say anything about how parts of a bound system should move - he only considers separate bodies. Moreover, while he says that "each falling body acquires a definite speed fixed by nature," it would be implausible to suppose that that definite speed is acquired instantaneously - presumably, some acceleration is taken for granted. So a charitable reading would say that when two separate bodies are dropped side by side, at some later time their speeds will "stand to one another in the same ratio as the weights."

Consider Galileo's setup: two bodies of unequal weight tied by a light string and dropped from a height. If at first the string is loose, the two bodies behave as separate bodies (notice how we are already importing our physical intuitions into the thought experiment!) If that's the case, then according to Aristotle, the heavier body will be falling faster than the lighter one, but that cannot go on forever: at some point the string will go taught. At that point we can treat the two bodies as one (again, a physical intuition). This combined body, if it stays whole (which it won't, but let's disregard that) will, according to Aristotle, eventually acquire a higher speed than either of the two separate bodies had before they combined. But as long as it behaves as one body, we cannot compare its motion to the motion of its parts, since the parts are not separate and independent, nor have they been falling side by side with the combined body: there was a discontinuous transition from two falling bodies to one.
So my conclusion is that Galileo's thought experiment, while suggestive (it seems implausible that the two bodies will lurch forward as soon as they come in contact with each other), doesn't constitute a reductio against Aristotle. -
Thought experiments and empiricismThought experiments are nothing but a form of empirical simulation. For any thought experiment can be substituted for a publicly demonstrable virtual reality simulation. — sime
Thought experiments can be more than that. Some thought experiments explicitly assume counterfactual conditions, unphysical idealizations, etc. The interpretation, the lessons and the value of such gedanken are often controversial. -
Question about a basic syllogismYes, you are right, I interpreted 'are' as 'being equal to', not as class membership. Is thinking in class memberships the right way to approach syllogisms in general? I find it hard to determine what context I can, and cannot use, since, as I understand it now, in logic, we ignore anything that's not in the premises. — Ulrik
You would have to use a formal language to avoid ambiguities (e.g. ⊂ vs. =), but for relatively simple reasoning this isn't necessary. You just need to apply common sense or knowledge of the context to come up with the right interpretation.
But how about this famous argument from Aristotle, where he says:
If A is equal to B, and B is equal to C, then A is equal to C.
In this case we have to interpret 'equal to' as identical to, not as class membership?
If A = B and C = B, then A = C would be correct in that case. — Ulrik
IIRC this is true in Aristotelian logic, where certain types of predicates are simply assumed to be transitive. So this result wouldn't require proof. -
Thought experiments and empiricismSo, the doctrine that "knowledge is derived from the senses" is well and truly a dead doctrine, and I am thoroughly surprised if anyone is wasting their time on it. — Inis
Is this literally the doctrine with which Norton, Brown, et al. are concerned? Have you actually looked at any of the literature? Do you think it reasonable to believe that these and a sizable proportion of other contemporary philosophers would be "wasting their time" on something that is "objectively false" and "well and truly a dead"?
GRW is not quantum mechanics, Bohm has been refuted so many times it's getting boring, Copenhagen is psychology. These are all standard views in foundations of QM.
And, you call me "stupid"? — Inis
I have to say, you leave me little choice. -
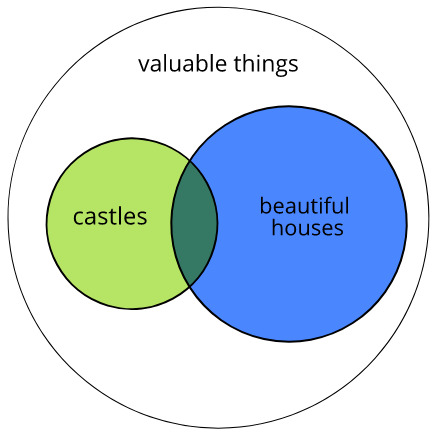
Question about a basic syllogismYour mistake is that you interpret "are" as identity (=), whereas from the context it should be clear that "are" here indicates membership of a class (of valuable things).
Such things are easier to understand if you draw a Venn diagram:
-
Is Determinism self-refuting?If pain has never been causal throughout evolution, then I can see no reason (i) why it should have evolved at all, or (ii) why it should be so unpleasant (if the subjective sensation is not what causes us to withdraw the finger and never has been, the sensation could just as well have been extremely pleasant, since pleasant or unpleasant, it would have made no difference). — Herg
At best, pain signals us about some adverse environmental circumstances or a bodily disorder, so that we attend to this situation and deal with it. But of such situations those in which unconscious reflexes (like yanking a finger out of a fire) are adequate and sufficient are relatively few.
Why is it so damn unpleasant? And why do we feel it, even when there is nothing we can reasonably do about its cause (without the amenities provided by our modern civilization, which evolution could not have anticipated)? Well, evolution is primarily a satisficing process, rather than an optimizing one: it often settles on a good-enough solution. It must be that occasional bouts of misery did not impose as high a cost on reproductive success as the alternatives that were available at the time.
Besides, though I am no more an expert in this area than you are, surely unconscious reactions would have evolved much earlier than anything like pain? Even organisms without any central nervous system have those.
How does that challenge work? — TheMadFool
Well, different people have posed it somewhat differently, and you'll have to read their arguments to understand. Though sometimes simply, even flippantly stated (like Sir Eccles' quote in the OP), it's not so simple really. In my opinion, James Jordan's statement that I quoted in this post is one of the most cogent. -
Evolution is harder with currently evolved organismsWhen I look at current organisms, I see them as very complex and rigid, especially to the extent that their malleability solidifies towards their surrounding environment. At the onset of evolution, simple organisms were more malleable to the variables surrounding them, so changes occur at a fast pace, but as these organisms progressed with due millions of years, their malleability became rigid which is why you don't see evolution occuring today. — Susu
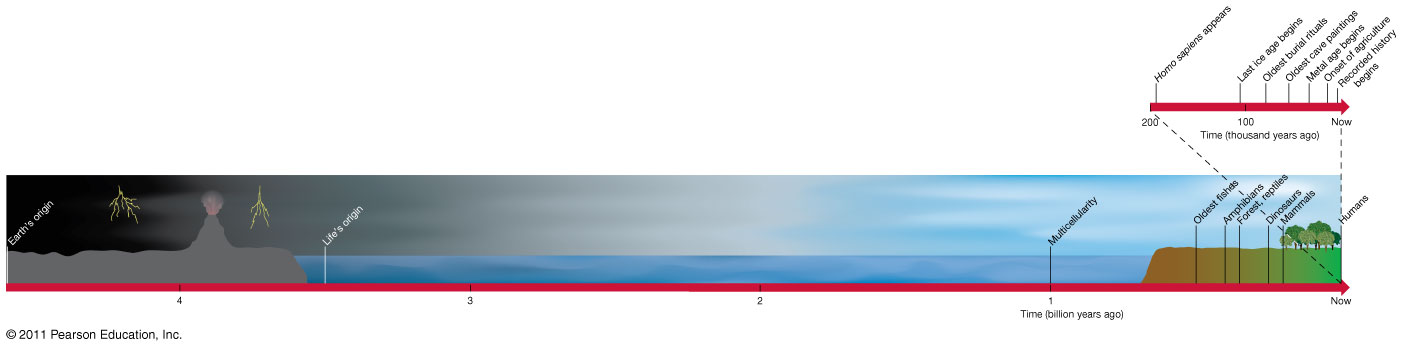
I think you got this idea because you don't have a good feel for the timescales involved (that's OK, most of us don't). Life has been on Earth for about 3.8 billion years - that is, practically since the surface of the planet cooled and stabilized enough for life to be at all possible. But for the first two billion years there were only bacteria-like organisms. Only then did the first organisms of a different kind appeared, from which plants and animals would eventually emerge. From there multicellular organisms took up to a billion years to evolve. Animals in their more-or-less recognizable form (things like molluscs and sea cucumbers) appeared only about half a billion years ago. And evolutionary biologists have been observing evolution in our time for some decades. Decades. Think about it.
Here is a rough timeline in scale:
-
Thought experiments and empiricismThis post would benefit from some background reading suggestions for those who do not know what you are talking about.
John Norton, Why thought experiments do not transcend empiricism (2002)
James Brown, Why thought experiments transcend empiricism (2004)
John Norton's other publications on the topic.
SEP Thought Experiments -
Is Determinism self-refuting?My suspicion is that these properties are now epiphenomenal, but were not always so. Consider the pain you feel when you burn your finger. Scientists tell us that you snatch your finger away before you feel the pain, suggesting that the pain is epiphenomenal; but why have we evolved to feel the pain, if it serves no causal function? I think perhaps pain was causal millions of years ago, but then animals evolved a faster response system that by-passes the pain, leaving it as an epiphenomenon. — Herg
So suppose, as you say, that in our evolutionary past pain (qua mental state) served a causal function. Does that mean then that the neurophysiological states that realized this mental state were epiphenomenal? How would that work? -
Pew Survey: How do European countries differ in religious commitment?Here is Levada-Center, a reputable Russian research center:Religion and superstition survey conducted in Russia over a number of years.
Self-identified as Orthodox Christian: 75% in 2017
"I know without a doubt that God exists": 25% (2015) - 31% (2017) (cf. 25% between 2015-2017 in the Pew survey - a good match)
So, three quarters self-identify as Orthodox, but only between one quarter and one third are sure that God exists. Indeed, among "Orthodox" the percentage is only slightly higher: in 2017 34% are sure that God exists, and "one out of every eight... doesn’t believe in God or isn’t sure whether God exists."
There is self-identification (which is what authorities care about) and there is belief - not the same thing. And only a small percentage of self-identified Orthodox are actually observant to any significant extent. But that's not unique to Russia. In the US, for example, people will say that they are "Catholic," but oftentimes they mean nothing more than that they come from a Catholic family (which may not have been particularly religious either). "Jewish" self-identification is even less correlated with religion.
SophistiCat

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum