I'm not saying that (in this example) it's completely independent of empirical evidence, just that both sides of the debate accept the same empirical facts, so the debate is not about which set of facts obtain. Those who think there "really are" species and those who think there aren't don't argue about what organisms exist and how similar their genes are to each other. They've all got that same empirical data, and are arguing about what is the best way of organizing our thoughts about that data.

Neither side could demonstrate the difference between a world where "species exist" and "species don't exist" through Snakes' "novel test", for example. Both sides would describe the current world as a world where their personal position is true, and... probably be stumped to describe what is different about their opponents' world, or else put forward a description that their opponents would say misrepresents their view.

It's like interpretations of quantum mechanics. Copenhagen fans and MWI fans and Pilot Wave fans and so on all agree about what equations accurately describe the observable world. They disagree about what is the most useful way of understanding or interpreting those equations. That is the essence of a philosophical disagreement.

This article you linked is a great example of metaphysics (or philosophy in general) done right. What that author is arguing is essentially that “species” is not a useful or coherent concept, it is a concept that gives rise to unnecessary confusion and unanswerable questions, so that concept and the framework that surrounds it are best abandoned and replaced with alternative ways of thinking about things that serve the same purpose without leading into those same problems.

Whether species exist or not isn’t an empirical question. People arguing that species do exist will do so on the basis of the same empirical facts as people arguing that they don’t exist. The argument isn’t about those facts, but about how to think about those facts. Likewise for arguments about whether universals are real, etc. It boils down to “is this a clear and useful way of thinking about the world”?, not “is this how the world is?”

The mods, obviously, but I think your actual question is "what are the criteria for philosophy?", and I think the answer to that is "is it just expressing an opinion or is it giving some kind of thoughtful reason why one viewpoint is more correct than another?"

As I recall, the cub scout oath contains language by which the scout promises "to be square and obey the law of the Pack." Perhaps that's what it is to be honorable. — Ciceronianus the White

It literally has “honor” in it:

On my honor I will do my best to do my duty to God and my country and to obey the Scout Law; to help other people at all times; to keep myself physically strong, mentally awake, and morally straight.

I can't remember what being square is — Ciceronianus the White

Being square or straight, in many languages across history, means to think or behave rightly or correctly; all these words have literal etymology connections.

I then realized that theism is, at its core, a belief that there is a being whose commands one has to obey without question — TheMadFool

That’s not so much theism as it is divine command theory. Not all theists subscribe to that.

...and their arrangements?

A 200lb pile of graphite and a 200lb solid diamond grandfather clock are both just 200lbs of carbon atoms, but the arrangement of those atoms makes all the difference. Saying that does not go against the reducibility of them both.

Yeah, reductivism has to be monistic, so it rules out substance dualist accounts of mind, vitalist accounts of life, etc. But in saying that chemistry reduces to physics, we don’t say chemicals don’t exist. Likewise in saying biological reduces to chemistry, we don’t say life doesn’t exist. And in saying psychology reduces to biology—the mind is just what the brain does—we don’t say that minds don’t exist, or aren’t important, or anything like that. Just that the complex upper levels are analyzable in terms of simpler lower levels, all the way down to the simplest of things.

Reductionism is not eliminativism. Saying that mind is reducible to matter isn't saying that mind doesn't exist, any more than saying that you can construct rational numbers out of equivalence classes of integers means that rational numbers don't exist. Reductionism just says that one thing is made entirely out of another thing, not that the former doesn't exist at all and only the latter does.

No, in a nondeterministic world free will has the possibility of existing, which it doesn't have in a deterministic world. — Lida Rose

But you said earlier that "Whether an event is wholly determined, wholly random, or a combination of the two, it robs the will of all freedom to create it." A non-deterministic world is just a world with randomness; randomness is the lack of determination, determination is the lack of randomness. You said as much in the OP, when you wrote "There are only two ways actions take place; completely randomly, or caused." For every event, either there is sufficient cause to explain it happening, in which case it is determined by those causes, or whatever causal influences there may have been on it are insufficient, to some degree it happens "for no reason", not because of anything, just at random.

If determinism (everything happening from exact causes) and nondeterminism (some things happening just at random) both undermine the possibility of something you're calling "free will", then you the thing you're calling "free will" is a useless concept that doesn't signify anything. You can't tell any difference between "free will exists" and "free will doesn't exist", if "free will" means what you take it to mean.

But there are other, more useful concepts that also answer to our folk concept of "free will", and have nothing at all to do with determinism or randomness. Like I already gave before.

I don't know if it makes any difference, — Lida Rose

Nope, my response would have been the same.

what I meant to say, but was unable to correct — Lida Rose

Did you see my tip for how to edit earlier?

Click the little pencil icon below and to the left of your post. You may need to click a "..." icon there first, to reveal the pencil icon.

And, just what are these relevant possibilities? — Lida Rose

The way you construe free will, the relevant possibilities are a determining world and a nondeterministic world. Free will as you construe it stand the same (impossible) in either scenarios, and so doesn’t really mean anything. What would “having free will” look like, in an imaginary world where you had it? That imaginary world can’t be deterministic, and it can’t be nondeterministic, so what would you actually imagine “free will” to be?

The way I construe free will, the relevant possibilities are things like an alcoholic resisting the urge to drink (if she is able to do that, she has free will in that moment) versus an alcoholic trying but failed to resist the urge to drink (in which case her will was not free in that moment).

A gave a more useful concept that actually distinguishes between things we care above early in the thread.
— Pfhorrest

This isn't making sense. Please rephrase. — Lida Rose

I mean the bit I said earlier:

Will is desire. Free will is when you are free to desire what you desire to desire. When wanting to for a certain want to be the want you act on causes that want to be the want you act on. — Pfhorrest

Whether an act is wholly determined, wholly random, or a combination of the two, it robs the will of all freedom. — Lida Rose

That conclusion suggests you’re employing an incoherent notion of “freedom” that doesn’t actually distinguish some possibilities from others, since in every possible scenario it renders itself impossible.

A gave a more useful concept that actually distinguishes between things we care above early in the thread.

Every action has an equal and opposite reaction. When you push the ship the ship pushes back on you. The force applied to it and to you are the same. Since your mass is much smaller, the force accelerates you more. But the ship still accelerates too, just less so in proportion to its greater mass.

Imagine a spectrum of examples to illustrate. You push a person the same mass as you: you both accelerate away equally. You push someone slightly more massive than you: you accelerate more and he accelerates less, but you both still accelerate some. You push something much more massive than you: you accelerate a lot more and it accelerates only a little, but still you both accelerate some.

I never ever heard of the Tulsa and Rosewood massacres until last week. — Benkei

The first I heard of them was in the opening of the first episode of the Watchmen TV show. At first I assumed it was a historical difference in the alternate timeline of that franchise, but then I looked up what “really” happened in Tulsa as I figured there must have been something significant if that was a point of historical divergence they chose to highlight... but nope, that’s what actually happened, holy shit, why didn’t we learn about this in school.

How could it not be determined? — Lida Rose

I just mean that it doesn’t matter how well determined the process is, how much randomness features in it; it doesn’t matter for the purpose of freedom.

Just do the math in your own equation. F = ma, correct. If F and m are nonzero, then a is nonzero. Plug in whatever force you can apply with your finger and whatever you look up the mass of a cruise liner to be and find the nonzero acceleration you could apply to it. It will be very small, but not zero.

Yes, absolutely, but because the force would be small and the mass large, the acceleration would be very small. But it would still be something: in the absence of any friction, the cruise liner would slowly begin moving, faster and faster the longer you kept pushing.

But why is one desire ultimately more persuasive than another desire? And how did that "more persuasiveness" arise? — Lida Rose

A variety of complicated psychological and neurological reasons, that aren't especially relevant at this stage of discussion. (They become relevant in discussions about how in practice to increase one's freedom of will, but that's a study for psychologists, not philosophers, as it's about the contingent ways that human brains actually work, not about necessary a priori concepts.)

The processes that lead to that outcome could be determined or not, but if we want hope of being able to direct those processes, they better be at least adequately determined, because there's no controlling a figurative roll of the dice.

First you said that will is desire, "Will basically is just desire," but now you're saying that will that's free controls desire. Free will controls itself? Fine, but then something has to work as a causal (deterministic) agent. — Lida Rose

Will is desire. Free will is when you are free to desire what you desire to desire. When wanting to for a certain want to be the want you act on causes that want to be the want you act on. Yes, that's completely deterministic; indeterminism has nothing to do with this, other than possibly as an impediment; indeterminism is just noise in the process that at most could screw things up.

This is best illustrated with examples. Sometimes we want things that we want to not want. A reluctant drug addict wants to take drugs, and wishes that they didn't want to take drugs. It's a second-order want: a want about wants. They want to get over their addiction, and to stop wanting to take drugs; or at the very least, they want to not act on their desire to take drugs. Their will is free to the extent that they are able to control at least the relationship between their desires and their behavior, if not the desires themselves.

Free will is the ability that lets someone resist from taking a drug even though they really really want to, and possibly even lets them stop wanting to in the first place. It's not some magical intervention in the causal processes, it's just a functional state of the mind and brain: a state where thinking something is or isn't the best course of action, reflexively judging one's own desires as the right or wrong things to desire, is causally effective in making one have or not have, or at least act on or not act on, those desires.

Thanks. But no ability to edit? Boy, that's almost a membership breaker. — Lida Rose

Click the little pencil icon below and to the left of your post. You may need to click a "..." icon there first, to reveal the pencil icon.

Will is the capacity to act decisively on one's desires.

Free will is to do so undirected by controlling influences. — Lida Rose

Will basically is just desire, specifically whichever desire it is that ultimately moves you to act.

Free will is the ability to control what you desire, or at least which desire it is that ultimate moves you to act.

To be free of will, in the useful functional sense above, is for your desires about {which of your desires are causally effective on your behavior} to be causally effective on your behavior.

That requires that the function of your brain be at least adequately deterministic.

To be free of will in the sense of being free from determination is not only useless, but counterproductive, leaving your actions random, uncontrollable by you, and so you unaccountable for them.

Interesting! Roe v Wade and unleaded gas started the same year.

Data across counties for a single year doesn’t help, we need data over time, for anywhere besides the US, or for the world globally.

The point of all of this is that there is already a well-known explanation for violent crime dropping (in principle anywhere, but definitely in the US) since 1990, one independent of anything to do with police or guns. That is a counterpoint to your claim that it went down in that time period because of increased police in that period.

You claimed that is hasn’t gone down elsewhere. (Which it should, if it is all about atmosphere lead). I can’t find any data on trends over time elsewhere. You presumably have some, if you’re making a claim about it. I’d just like to see it.

So no actual data on whether international crime rates correlate with atmospheric lead like US crime rates do?

So where is your claim that crime rates have not gone down elsewhere coming from?

A general graph of international rates would be fine, that’s what I was trying and failing to find.

Yes, but crime rate has not fallen in OTHER PLACES. — ernestm

Share some graphs of crime rates in other places please, I can only find US data.

Maybe if you actually read the linked article you would see plenty of people far more talented than me have already pretty rigorously established causation there, and that was precisely the reason why leaded gasoline’s was banned.

I’m curious your thoughts on my phone buying habits. I’ve discovered that when a model of iPhone gets discontinued, I can get one of those just-discontinued models for a dollar from my carrier. I presume because they were otherwise going to dispose of them. So when I find myself in need of a new phone, which is usually only when my existing one stops working for some reason that can’t be repaired, I get whatever just-discontinued thing that was probably about to be trash.

Responsible enough?

I was originally going to be end my post with exactly that joke and a comment about correlation and causation, but then I thought it would undermine my main point: that there actually is a plausible causal correlation between atmospheric lead and crime which explains the exact time frame of crime decrease @ernestm was talking about.

Violent crime worldwide has been dropping since about 1990 because childhood blood lead concentration has been dropping because atmospheric lead has been dropping because leaded gasoline has been phased out since the early 70s. There’s a 20-year delay because those lead-poisoned kids have to grow up first before they can be counted in crime statistics.

Crime rate also correlates with atmospheric lead, which has been decreasing steadily since the 1970s.

https://en.m.wikipedia.org/wiki/Lead–crime_hypothesis



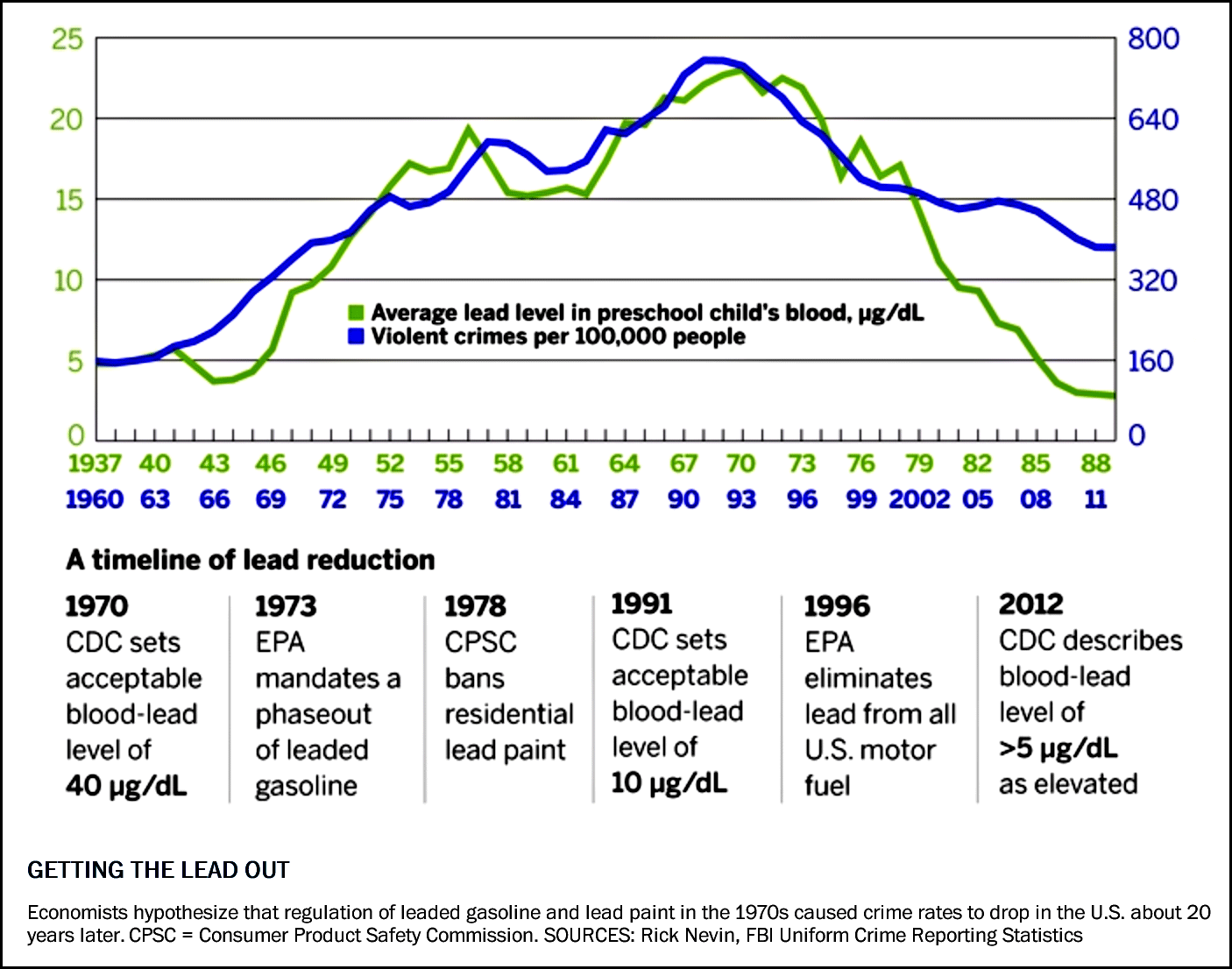
Oh look the peak of the delayed reaction was in 1990...

But before you can conceive of a phase space, you have to conceive of a theory that gives rise to that phase space. The phase space is just a slice of the theory; you need to lay out the theory first. — SophistiCat

This is exactly what I was refuting in the quoted bit. I suspect maybe the word “phase” is leading you to this conclusion, because a phase implies a temporal process, which is why I also named the synonymous term “configuration space” which has no such connotations. You don’t need any notion of time or any specific theory incorporating time to have a notion of there being multiple possible ways a thing could be. A configuration space is just a map of those possibilities. That has use in theories of dynamics to plot phases of cyclical processes, but you don’t have to think of such a theory before you think of the more general tool of a configuration space.

State agents can subvert and undermine or even be traitors to state policy, but, as you clearly agree, we can't expect this to be the norm; so, what we expect from state agents will follow from our evaluation of the state as a whole. — boethius

My point though is that being a participant in an institution the state tries to coopt does not make you a state agent. The state tries to coopt every institution, but clearly not every participant in every institution a state agent.

psychologists or other state agents (they have been selected, either way, because they believe the state is legitimate). — boethius

Tony Gibson was an English psychologist and anarchist. (First google result for anarchist psychologists.) As an anarchist he obviously didn’t believe the state was legitimate, but he was still a psychologist nevertheless. Which disproves your quoted statement as an absolute truth.

I’m not questioning your general thesis that (of course) the state tries to coopt the institution of psychology to it own ends, like it does every institution. Just saying that you can’t dismiss every participant in every such institution as an agent of the state. It’s not like politics where the very function of the institute is statist. There are people in every institution the state tries to coopt who don’t go along willingly if at all, and though the state tries to get rid of them when it can (of course), it’s usually not completely successful, and sometimes not very at all.

Did you know a disproportionate number of engineers get drawn into terrorist organizations? Does that make all engineers agents of terror?

Short version is I am also anti-foundationalist like Sellars, and not trying to push foundationalism in the part you quoted. Experiences are not opinions: they (and logical consistency) are what we criticize our opinions with.

The part I wrote immediately after the part you quoted is the critical/falsificationist/anti-foundationalist part:

Then we should devise models, or theories, that purport to satisfy all those experiences, and test them against further experiences, rejecting those that fail to satisfy any of them, and selecting the simplest, most efficient of those that remain as what we tentatively hold to be true. — Pfhorrest

The experiences are the things we’re trying to explain with our theories, but they don’t uniquely determine any particular theory. Every theory (and piece thereof, including more simplistic concepts) is initially equally tenable, not because it’s grounded in some foundational beliefs but because the default initial state of everything is “tenable”: then we check each of the options for success against our objective (explaining our experiences) and eliminate those that fail.

Also, that bit about interpretation you quoted is meant mostly to spell out how science differs from just polling people on what they think they saw, and compare that to how I say to conduct a moral investigation vs just polling people on their desires.

I think you're missing the point of where I'm going with this.

A phase space, or configuration space, doesn't have to imply anything about time being presumed simply to conceive of that space. It's just a spatial representation of all the different possible states that a system could be in.

A span across such a phase space is thus a pattern of change: the system moving from one state to another through a succession of intermediate states. This is still before we have constructed any notion of time, just a span of possibilities, without any particular directionality to them; we could, so far as we've conceived thus far, scrub back and forth across that pattern of changes willy-nilly.

Time is most generally a measure of changes in the universe, so a span of time is a span of some sort like that, through the phase space of the universe, with every possible point in that phase space representing some possible state of the universe.

But time as we normally conceive of it is directional, so not just any span of the phase space counts as a span of time as we normally conceive of it. A universe at maximal entropy, for instance, may find itself wandering around through a bunch of possible states in no particular pattern, sometimes even repeating the same state, but we wouldn't normally describe that as time running forward and backward in time in such a universe. Rather, time has effectively stopped in such a universe: all those different maximally-entropic states are "the same time", because they're all the same distance along the direction through the phase space in which we reckon time to point: the direction from less entropic states to more entropic states.

The phase space of the universe being more entropic in one direction and less entropic in another is an anisometry: it's not the same in both directions. But the phase space is not globally more entropic in one direction and less entropic in another, so that anisometry is only local. You could look along the less-entropic ("past") direction until you hit a local entropic minimum, and then if you keep looking further in that same direction, you'll see entropy going up again, so locally (in the phase space) that direction is now "the future", even though it's the same direction that elsewhere (in the phase space) it's "the past". That local entropic minimum is "the beginning of time" from the perspective of states on either side of it.

We reckon less-entropic states as "past" and more-entropic states as "future" because memory-formation, like all processes, necessitates an increase in entropy, so the states of the universe that we remember are necessarily less entropic than the current state of the universe, and as we project patterns in those memories beyond the present, we construct an idea of the future.

There are necessarily more high-entropy states than low-entropy states though, so for every point in the phase space, more adjacent points are "immediate possible futures" than are "immediate possible pasts". Because of this asymmetry, possible pasts converge, while possible futures diverge. The further into the past you look, the more determined the universe at that time is. I.e. there are fewer possible states of the universe connected to the present state of the universe through incremental steps through the phase space toward less-entropic states, the more steps you take in that direction. In the limit, there is only one local entropic minimum, one beginning of time. But the further into the future you look, the less determined the universe at that time is. I.e. there are more possible states of the universe connected to the present state of the universe through incremental steps through the phase space toward more-entropic states, the more steps you take in that direction. In the limit that direction, you get the heat death of the universe, the "end of time" even though it's not the end of change, because all change is now inconsequential and directionless, no state of the universe is a possible future, they're all either equally present or else past.


(Oh and as for the "possible worlds" bit, that's because I consider this a form of modal realism, but with possible worlds more like Kripke's than like Lewis'. Lewis' "possible worlds" are more like time-lines in this model, while Kripke's possible worlds are more like possible configurations of the universe, points in the phase space, in this model. "Accessible possible worlds", in Kripke's terminology, are basically synonymous with "futures" in this model; other non-accessible possible worlds are either pasts relative to the actual present, or else counterfactual, "alternate timelines".)


FWIW, this isn't at all contradictory with "time is what a clock measures". A clock is just a system that undergoes routine, patterned changes, which is excellent for measuring distances across a configuration space, just like a ruler with its routine, patterned markings is excellent for measuring distances in ordinary space.

Well it's either that or sort of like a ball of timey-wimey, wibbly-wobbly... stuff.

The dimension across which that gradient occurs is a dimension of the phase-space. The gradient gives directionality to a span across that phase-space. Without that directionality, a span of the phase-space wouldn't be recognizable as time, so the existence of that gradient in the phase-space is what constitutes the existence of time as we mean it.

Time is a local entropic anisometry in the phase space of possible worlds.

I thought you were replying to Judaka's post about "economic redistribution based on race", the point of which was, I thought, that economic redistribution to make up for past injustices shouldn't be limited to any particular race (or anything else), just helping whoever needs help for whatever reasons.

Maybe I was mistaken.

Weren’t you just agreeing the other day that class-focused amelioration of poverty regardless of race is fine, since race correlates with class and so helping poor people in general automatically helps black people disproportionately more than whites, since blacks are disproportionately poor?

You’ve got it right.

:up: