Comments

  • Logical Nihilism
    When I gave some arguments against square circles, I suggested that one could quibble with the arguments, but not oppose them in any way that goes beyond a quibble. I think that has turned out to be right. — Leontiskos

    As you like.

    It seems to me you think this is a question that can only ever be asked in one way and in one context, and therefore it only ever has one answer.

    You can do that, and you can be right. Your response to a counterexample is "Well I didn't mean that, I meant this" and your honor is preserved. In the context you had in mind, you're still right. The counterexample isn't one.

    Pick up a length of pipe. Look at it from the side and it's rectangular. Look at it straight on, it's circular. Done. "But I didn't mean that."

    But you also seem to think the context you have in mind for any question that arises is the only context it can possibly arise in. I tend to have less confidence in my own omniscience, but you do you.
  • Logical Nihilism
    I would need to sit down with some algebra to understand it properly though. — fdrake

    If I'm doing something dumb, it's okay to just say that.

    Regarding the projection - there will be a lot of degrees of freedom if you get to choose an arbitrary projection onto the plane — fdrake

    Yes exactly.

    Here again is how I got here.

    In school, we learn to think of circles this way:
    1. You've got a plane.
    2. Pick a point in the plane.
    3. Find all the points in the plane equidistant from that point.
    4. That set of points is your circle.
    5. The point you picked in (2) is the center of your circle.

    But it needn't be that way.

    Your great circle example, or the conic sections we learn in Algebra II, are different.

    1'. Pick a point in 3-space.
    2'. Find all the points equidistant from that point.
    3'. That set is a sphere, or a 2-sphere.
    4'. Any coplanar subset of the points in (2') is a circle, or a 1-sphere.

    If you now look at the plane of the the circle in (4'), there is a subtle difference from the plane in (4): the center is not marked. No point in the plane was used to generate the circle ― although, of course, the circle has a center you can find. But in the schoolboy's circle, you never have to go find the center ― you pick that point to start with.

    (There's a direction-of-fit thing here: in one case, the center determines the circle; in the other, the circle determines the center.)

    When you find the center, you might ask, is it related in any special way to the point in 3-space we picked (1')? And of course it is. There is exactly one line orthogonal to the plane that passes through that original generating point, and it passes through the plane at the center of the circle as well.

    And you might then think of the center of the circle as a projection of the center of the sphere. And it is, but it's entirely optional. That projection comes after we already have the circle. It's the canonical projection alright, but you could also project that point to any point on the plane, because this projection is just a thing you're doing ― the circle doesn't need it, isn't waiting for this projection, you see?
  • Logical Nihilism
    ↪fdrake


    There's nothing much to the geometry, but here's a picture to start with.

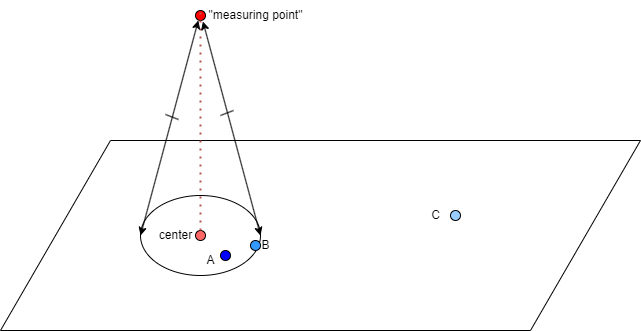
    diagram1.png

    (There's other ways to look at this. You could of course go ahead and treat the "determining point" as a center and make a circle on a plane right there, then project that circle onto a parallel plane. Blah blah blah.)

    Having separated the point that determines the circle from the center of the circle, it just occurred to me that you could treat it separately, do a lot of stuff with it. To start with, you don't have to project to the center of the circle in the plane, you don't have to use that orthogonal projection, but could send it (translate it) to any point A, B, or C, anywhere in the plane.

    Then I thought there might be something interesting if you grouped these projections into buckets, those that send it into the circle, those that send it far away, and so on. And I thought there might be some interesting stuff there ― maybe allowing the axis to wobble a little, and see how stable your buckets were, and lots of other stuff.

    But then it occurred to me what probably caught my eye about this.

    If instead of thinking of the points A, B, and C as being projections of the "determining point", what if you went the other way, and thought of any point in the plane translating to the point off the plane that determines this circle.

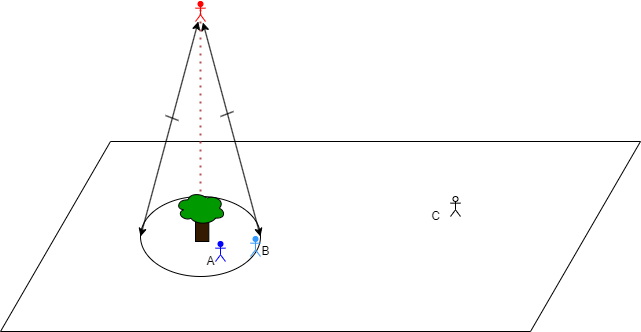
    diagram2.png

    Suddenly that cone looks like a field of vision, and the other points are other actors who are triangulating their view of ― in this case ― a tree (or whatever) with the red guy at the "determining point". (We'd probably want to move the red guy onto the plane with the A, B, and C, and create a new notional plane orthogonal to this one to represent Red's f.o.v., but whatever. At this point the whole setup is merely suggestive.)

    And then it should be obvious there is a meaningful difference between being in the circle and outside it, because that determines whether you are also in Red's cone of vision.

    It happens I've been reading about triangulation and joint and shared intentionality in apes and humans (Michael Tomasello), so it was probably on my mind, and that's why the whole arrangement, splitting one point into two (center/determiner), then splitting that second point into two as well (determiner/projected) ― it all suggested something to me, and this was probably it.

    I wonder if there is something else interesting just to the geometry, but that's no doubt above my paygrade.
  • Logical Nihilism
    I would quite like you to draw this — fdrake

    I'm glad you came back to this, and I'm going to draw some pictures. I had decided last night there was nothing here and I don't know why I was going on about it, but I have an idea now!
  • Logical Nihilism
    ↪fdrake


    I guess once you have the "axel" in mind, you could say that choosing the point where that line intersects the plane of the circle as the point that "determines" the circle is natural and convenient, but just a convention. The radius and center and plane of a circle determine it, but so would an infinite number of pairs of points and distances.

    *** If you think of the determining point as the vertex of a cone, there are an infinite number of cones, all sharing an axis, the circle is a section of.
  • Logical Nihilism
    ↪fdrake


    I'll draw if I have to, but I think I can clarify it verbally.

    1. Pick a point and a length.

    These together determine a bunch of circles in 3-space.

    2. Pick one.

    If you picked one that isn't coplanar, there's a projection of the "measuring point" onto the plane the circle is in that preserves the property of being equidistant from points on the circle, in fact preserves it as you move the point toward the plane, shrinking your originally chosen length until it's the radius of the circle.

    But there are other projections where that original point will land off-center, or on the circle, or outside it.

    If you want to go backwards, you need an additional constraint**, because there's a whole line of possible "measuring points" through the center of a circle, perpendicular to its plane, like an axel. Your measuring point could be projected to anywhere in the plane, and any point in the plane could be projected to anywhere on that axel line.

    You could also play with projecting the circle and the point onto yet another plane.

    It's just curious that you can separate the point that generates the circle from its center, that those are two different properties, and there are projections that will separate them in a plane.

    ** The original length gives you two, I think
  • Logical Nihilism
    ↪fdrake


    Yeah I was only thinking about the point being away from the plane, no other fiddling. If I've ever considered that, it was so long ago I've forgotten.

    It's just a curiosity that talking about the center of a circle is a little over-committal. It's the center, coplanar, only under a particular projection onto the plane of the circle. But under other projections, the "center" lands elsewhere, which for some reason seems really cool and even useful to me.
  • Logical Nihilism
    A set of coplanar points equidistant from a point in the plane of coplanarity. — fdrake

    Does that point need also to be coplanar? Is there a counterexample I'm missing?

    The cross-section of a hollow sphere will be a circle regardless of whether I imagine a point at the center or not. — Leontiskos

    You realize that on the sphere it's just a straight line, I hope.

    ―― I don't know why I'm participating in this.
  • Logical Nihilism
    Planes and points cannot be stipulated to exist or not exist. — Leontiskos

    I did no such stipulating. Look again.

    Your word "imagine" is on point given my earlier claim — Leontiskos

    And you are ignoring the fact that I used it twice.
  • Logical Nihilism
    but it does not satisfy Euclid's definition of one verbatim — fdrake

    I think it does. You've only asserted otherwise, you haven't shown it.     — Leontiskos

    He doesn't need to. The sphere is a 2-manifold, and his great circle is a set of points on that manifold. There are no planes here, nothing else, only the points on the surface of the ball.

    You are imagining the sphere embedded in the usual 3d Euclidean space. Now, imagine it isn't. There is no point the points on this great circle are equidistant from.

    As for me, I mean a set of points equidistant from a point. — fdrake

    But don't you need to specify coplanar? If we're in 3d space, you've defined a sphere, in 4th I guess some sort of hypersphere, I don't know, blah blah blah.
  • Logical Nihilism
    Not for nothing, but a square is an approximation of a circle. A better approximation than an equilateral triangle, but not as good as a regular pentagon.

    But then, who would ever consider approximating curves with straight lines? Ridiculous idea.
  • Logical Nihilism
    your made up "taxicab geometry" — Leontiskos

    He didn't make it up.
  • A challenge to Frege on assertion
    ↪fdrake


    Huh. Whaddya know.

    tonal language — Leontiskos

    Yeah that's nice, I forgot about tone. (I really should learn something about how it's used in such languages.)
  • A challenge to Frege on assertion
    ↪fdrake


    Thought it might have been him.

    On the one hand, it's a ridiculous point because you can't *say* one word on top of another -- gotta say them in order. But on the other hand, spoken language is pretty much always accompanied by gestures, so you can imagine an accompanying gesture to convey the "on". On the third hand (the gripping hand), this won't work over a telephone. But on the fourth hand, language is spoken in person long long long before telephones, and pretty damn long before writing. And even writing has its own story, a little different from the story of speech.
  • A challenge to Frege on assertion
    I don't even think you can get "sitting on" to be isomorphic, since the words don't do anything like that; one merely precedes the other. — J

    1. They could. I forget who this was -- LW? Sellars? I don't know -- but someone pointed out that you could write

      cat
      mat

    for "The cat is on the mat".

    2. Anyway, the whole point of the "logical form" thing is that there is something we happen to represent in particular ways in particular languages using sentence structure, but that structure is not the logical structure, just how we represent it.

    It's one reason people are sometimes inclined to posit a "language of thought".

    3. I think the isomorphism thing is not crazy. In order to say that a couple things are related in a particular way, appropriate to those things, you combine names for those things in a particular way, appropriate to names of things.

    Not crazy, but the trouble is it sounds easy to put this into a theory and it turns out to be hard.

    4. Probably because it's a fundamental mistake to think that language has the same kind of structure you think the world has. Not crazy, but wrong, and understandable, though why we think this is itself an interesting puzzle.

    The very idea that in language we represent the world, is probably a sort of illusion, or a myth.
  • A challenge to Frege on assertion
    ↪J


    He seems to think there's a sort of isomorphism here, that atomic propositions are structured as atomic facts are structured. It's why you can use a sentence or a picture or a model or the actual things to say something.
  • A challenge to Frege on assertion
    So if not in appearance, where are to we to find the similar form? — J

    In the Tractatus.
  • Plato's Republic Book 10
    ↪Metaphysician Undercover


    Found the reference to Homer's muse, a little later, but alas it's the "pleasure-giving Muse" (607a-c), not the "true Muse -- that of discussion and philosophy" (548b).

    Not question-begging at all.

    Carry on.
  • Plato's Republic Book 10
    The whole point is that this, "the divine taking hold of the poet", is the false representation which Plato wants to rid us of. — Metaphysician Undercover

    The human being is a medium, an agent with free will, and is really speaking one's own opinions about the divine. — Metaphysician Undercover

    But this is just denying that divine inspiration is a thing. It was already clear what your view on the matter is.

    And maybe it's Plato's too.

    So Plato grasped a very difficult problem, which was the question of how forms, or ideas, could be causally active in the creative process. — Metaphysician Undercover

    But it's not the Forms that would matter here, but the Muses. And he doesn't seem to mention them. Maybe I overlooked it.

    But as near as I can tell no one is bothering to present an actual argument against the efficacy of the Muses in the production of Homer's poetry.

    Your incredulity is not an argument.
  • Plato's Republic Book 10
    We are inclined to believe that the poetry is a representation of the divine. But this leaves out the very important medium, which is the poet's own ideas of the divine. So the poetry really only represents the divine through the medium, which is the poet's ideas. — Metaphysician Undercover

    And if the poet is inspired?

    Are these two claims the same:

    (1) The poet expresses his ideas about the divine.
    (2) The divine expresses itself through the medium of the poet's ideas.

    The principal issue is the deficiency of the human mind, in its attempts to grasp "the ideal", as the best, most perfect, divine ideas. — Metaphysician Undercover

    But what if it is not the poet reaching out toward the divine ("Ah, but a man's reach must exceed his grasp, or what's a heaven for?"), but the divine taking hold of the poet?

    The argument would have to be that a poet's ideas (or his words, really) make too poor a material for the divine to use to express itself. But what is that argument?
  • A challenge to Frege on assertion
    ↪Leontiskos


    You know it's funny, but in what you might consider the early days of cognitive psychology, before there was much neuroscience, there was an enormous amount of research specifically on how children learn geometry. It was a core topic.
  • A challenge to Frege on assertion
    ↪Leontiskos


    Sure, sure. I, ahem, recollect the Meno and I know it weirds modern readers out. We'll do better than that. Unless I have nothing to say, then it's on you.
  • A challenge to Frege on assertion
    Again, for me it begins with the puzzle of the Meno. I want to say that if logic is artifice then knowledge is artificial. And of course some of what we involve ourselves in when we do logic is artifice, but that doesn't mean that there is nothing more than that involved. — Leontiskos

    This is good. I'll go look at the Meno (I think there's at least one thread on it here somewhere), and if I have anything to say, we can make a fresh start with that.
  • A challenge to Frege on assertion
    kimchi — Leontiskos

    Heh. I taught my phone "Kimhi" but it ignored me this time.
  • A challenge to Frege on assertion
    But the classical logician says that it's not a schematization at all — Leontiskos

    Well then that word is not neutral enough.

    We have on the one side,

    (A) "Dogs are nice"

    and on the other

    (B) "For all x, if x is a dog, then it is nice."

    We just need a neutral word for the relation between (A) and (B), and, if you start with (A) and recast it as (B), we need a neutral word to describe what you're doing there. Maybe you believe you are "revealing (A)'s logical form," and maybe you don't.

    And then of course there's

    (C) (x)(Fx -> Gx)

    and you have to deal with (B)'s relation to (C) and probably (A)'s relation to (C). And that's the whole set.
  • A challenge to Frege on assertion
    Each time you state the problem in terms of artifice or invention you fail to capture a neutral (2). Do you see this? — Leontiskos

    I do, absolutely. As I said, I'm largely a partisan against (3) so I'll keep making that case along the way.

    I'm not sure (2) can be presented neutrally, but I hope it can. And if it can't, I'll keep saying "invented" rather than "discovered".

    This looks like that same conflation between speech act theory and logic. — Leontiskos

    Not "conflation" but derivation. Here again, this may not contribute to a neutral presentation of (2), but I have to treat language as being first for communication and other uses come after.

    I don't think that quite forecloses (3). If you look again at musical notation, you can say there are patterns (the theory of harmony for example) that only really become apparent in this simplified form. And you can cheerfully claim that the move to notation *reveals* something that underlies the practice of making music. And so with Frege and his concept-script.

    All I'm arguing for is slowing down the moment of schematization so that we can see frame-by-frame what's happening, regardless what we say about how before and after are related. --- They are at least related, in a different sense, by this act, so understanding this act may, or may not, tell us something about how they are related in a more abstract sense (whether one or the other is foundational and so on).
  • A challenge to Frege on assertion
    (We are now knee-deep in the topic I was hoping would become a new thread. Is it worth breaking off? The general membership would find this topic more interesting than Kimhi's.) — Leontiskos

    But they haven't paid their dues! We've earned this, by banging our heads against Kimchi. Oh sure, they'll join in *now*, for the fun part, but where were they when we were slogging through the mud, I ask you.
  • A challenge to Frege on assertion
    ↪Banno


    I think I basically agree.

    I would make two additional points: there's also no reason to think there's only one way to make our thoughts or our expressions clear (contra Frege, who might agree with you, but think his logically perfect language is the solution); second, clarity is obviously negotiated between speaker and audience, and thus our practices of making better, clearer arguments arise from the efforts of ordinary speakers -- addressing such issues is part of speaking a language, and of thinking as a member of a group.

    It's why I keep harping on the usefulness of logic even while expressing doubt that our linguistic practice has a logical foundation. And logical analysis isn't appropriate for all things at all times.

    And very last point, or set of points. Consider again musical notation. It's a simplification and representation of the practice of playing music, as, in my view, logic is a simplification of how we think. It's a fantastic invention, crucial for cultural transmission, and so on. And when children learn music, their first steps require simplification, and this one is ready to hand. But there's much, much more to performing music than what's on the page, and no one would think of disallowing the introduction of elements not captured there. No one makes the mistake of thinking the notation is an *ideal* that performance should strive to reach. It's not even the foundation of music, but a minimal record of what has come before, and in that sense can be used as a kind of starting point. (And I suppose the same could be said for a record of the words someone has spoken.)
  • A challenge to Frege on assertion
    this discrepancy — Leontiskos

    How very peculiar.

    So we have (1) the primary phenomena, everyday language use and reasoning.

    Then there's (2) the way logic schematizes these.

    And there's the further claim that in carrying out (2), we see (3) the deep structure of everyday language and reasoning, the underlying logical form.

    My claim was that we can talk about (2), whether (3) is true or not, and even without considering whether (3) is true or not.

    It's the same thing I've been saying all along, that (2) doesn't entail (3).

    If it turned out (3) is true, then all our talk about (2) would count as saying something fundamental about (1). I'm openly skeptical about (3), but I don't believe I have to commit to (3) being true or false to talk about (2).

    All of this agnosticism about (3) depends on being able to formulate (2) neutrally. If you're a partisan for or against (3), you might not bother. I'm mostly a partisan against (3), but I hold out hope for a neutral (2) so that I can talk to partisans for (3) about (2), and maybe even (1), rather than just (3). And because I find (2) interesting and useful even though I doubt (3).

    (I didn't follow your reasoning that turned my "not necessarily" into an even bigger "necessarily not". I do hope this was clearer.)
  • A challenge to Frege on assertion
    I will be out for the rest of the day — Leontiskos

    And I'll get back to work.

    More response to your earlier post tonight, and then we'll go from there.
  • A challenge to Frege on assertion
    You seem committed to the position which says that we cannot say anything fundamental about language or reasoning itself. — Leontiskos

    Not at all. I'm contesting whether we should take Frege as having done so.
  • A challenge to Frege on assertion
    is said to express a complete thought, that can be true or false, by fiat, by stipulation
    — Srap Tasmaner

    I don't think Frege holds that such things can be true or false by fiat.     — Leontiskos

    Sorry. That was ambiguous. The assignment of the truth-value is done by judgment, not by stipulation, but that "Fa" is truth-apt, that it expresses a complete thought, is stipulated.
  • A challenge to Frege on assertion
    the logician and the speech act theorist use the word 'assertion' differently. Maybe the most obvious difference is that the logician need not speak or engage in interpersonal communication in order to assert. More generally, what this means is that the forces involved in logical acts are different from the forces involved in speech acts. Martin is an example of someone who is explicitly interested in the former and not the latter, at least in the paper cited in this thread. — Leontiskos

    (I've started the Martin paper, so I expect we can talk more about that soon.)

    I don't want to just rush to deny that this is so, but all we have so far is the typical philosopher's gambit: "And by 'assertion' I don't mean assertion in the usual sense, by 'force' I don't mean force in the usual sense, ..."

    Consider that we are discussing a man who thought it necessary to invent a language, separate from natural languages, that would be suitable for use in logical analysis. In Frege's language, a formula like "Fa" or "(x)Fx" is said to express a complete thought, that can be true or false, by fiat, by stipulation. Is it any wonder that his logic looks more like a branch of mathematics than anything else?

    Which, again, is not to say that it is useless, anymore than mathematics is useless. But what are we to say about its relation to human reasoning conducted in natural languages? Is it, for instance, reasonable to imagine that something like Frege's system *underlies* human language use? I'm skeptical. Even while allowing its usefulness.

    And that means what we say about logic is what we say about a certain approach to reasoning and language, a certain way of taking it, but we need not think we are saying anything fundamental about language or reasoning itself.
  • A challenge to Frege on assertion
    we now seem to be doing speech act theory rather than logic — Leontiskos

    Oh -- there are dots I didn't connect there.

    Part of my concern is, what are these statements, the Ps and Qs, we deal with when doing logical analysis?

    In a sense, I'm trying to flesh out @frank's point about context. There's obviously something to that, we all know there is. Is it just dealing with indexicals? Maybe making explicit common knowledge that's relied on? You might be able to convince yourself that turning a non-truth-apt sentence into a truth-apt proposition is only a little more complicated than substituting names for pronouns, only there's more of that sort of thing to do.

    But what if that's wrong? What if language never comes anywhere close to expressing a complete thought because that's not what it's for? What if language is all hints and clues and suggestions because the audience shares the burden of communication with the speaker?

    Logical analysis, when it deals with "bits of language," seems to set aside the communicative nature of language and pretend that by presenting what one side of a conversation says, or what they might say if they were more prolix, it can present an argument in its entirety.

    If that's false, what are we doing when we engage in logical analysis?

    ...

    Lots more in your post to respond to, but I wanted to get to this first.
  • A challenge to Frege on assertion
    I am not sure that in everyday language the content really stands apart from the force, at least in the sort of examples you have given. Something like, "The next town is like 70 miles," is rather different from what logicians do. Such a thing is implying via content, not truly separating force from content. — Leontiskos

    I just watched a bird land on a broken tree limb. It glided in to a spot less than foot from the tip, immediately trotted up to that furthest point, and then remained there for several moments looking around. The uttermost point on the branch was clearly its destination, but it got there not by aiming at it, which it was surely capable of doing, but by landing first at an easier spot and then making the short, easy trek there.

    There's reason to think conversational language use is always like this, that we always say less than we mean and count on the audience to fill in "the rest," though whether that results in complete, self-contained propositions we both affirm or just another satisficing shortcut, that's hard to say. (Was this bird at the *exact* tip?) How often do we even try to understand each other "completely," whatever that might mean, and if such a thing is even possible, rather than enough to get along in a given situation? (Does a broken tree limb even have a well-defined tip? Did the bird care?)

    One thing implicature suggests is that what the audience fills in can be pretty complicated, involving not just disambiguation and shared background knowledge but inference. It also goes with my other recent posts, in trying to suggest that force may not always fall into a neat taxonomy, and that even when some force is employed or conveyed it might still vary in its intensity. (A sentence can be a simple assertion about geography, but not intended to convey that information.) For example, the effect of an attempted cancellation of force by following something you've said with "Just kidding" is widely considered uncertain or partial. (When Moss is chickening out of the robbery he proposed to Aaronow, a whole spectrum of assertive force suddenly blossoms, from committing to considering to talking about it to speaking of it, "as an idea.")

    Now, there was a lot of talk earlier in the thread about whether a sentence could display assertoric force without being asserted, and it occurred to me something a bit like this is going on in teaching language, something that looks a little like use, a little like mention, but doesn't make sense as either. You have to use a word and show your use, but your use of it in the first place is not a normal use -- to inform, say -- but a use chosen just so that it can be shown. Some features of assertion have to be in place, but not in order to make an assertion.

    So I don't think it's helpful to think of utterances as having a content that can be "extracted," nor is it helpful to think they have or lack some stereotypical force.

    Instead, most utterances only contain part of a point, at best, so whatever you count as the content of a statement is an interpretation that depends on how you fill out "what was said," and the force of an utterance is often mixed or uncertain, so what you count as its force is primarily an indication of how you intend to take it.

    My point, again, being that logic makes choices about what to count as the content, what to say was the force, and these choices can be interesting, helpful, and defensible, but they are also underdetermined. Even if you have no expectation that logic can tell you "what's really going on" in language use, you can still get logic wrong by assuming it has to come out as one specific thing.
  • Poets and tyrants in the Republic, Book I
    ↪Jamal


    Maybe part of my good impression of Cephalus is that we know what the wealthy and powerful will do to Socrates, but here's Cephalus who says, "Socrates! So glad you're here. I wish you'd come see me more often." And when he has to go see to the sacrifice (meant to mention that, as @Amity did), he encourages Socrates to carry on the conversation with the young folks, so not evidently concerned they'll be corrupted.
  • Poets and tyrants in the Republic, Book I
    philosophy is only good when you're old and have nothing better to do — Jamal

    I wasn't talking about TPF, exactly.

    Still, as I recall, Socrates says he's interested in talking to him precisely because of his advanced age, and seems to hope it will be a more reflective time of life, when matters of the soul might loom larger than worldly affairs. And he crosses that interest with a question about his wealth, whether he can only spare his attention because of his financial security. (Maybe he doesn't specifically ask that, I don't remember, but he's interested in how much interest he has in money and why.)

    To me, the idea of old age being naturally a philosophical period strikes me as quite reasonable and very Greek, if I may say so. At the other end, Socrates tries to get at the (noble) young before they're too caught up in responsibilities and cares. Also natural and reasonable, in the same way.

    By "Greek" I mean that obsession with stages of growth and development, progression toward embodying your deepest nature, that stuff.
  • Poets and tyrants in the Republic, Book I
    Cephalus believes his money is power. It is used in his old age to protect himself. His only interest in being just is self-serving. He is persuaded by the fear engendered by the poet’s stories of what will happen to him when he dies. — Fooloso4

    Maybe it's just the phrasing, but that seems a little harsh. I had rather a good impression of the old man, and I thought Socrates did too. His age and circumstances allow him to be more interested in less worldly matters, like talking with Socrates, which won't make him or his family any richer.
  • A challenge to Frege on assertion
    Aaronow: Yes. I mean are you actually talking about this, or are we just.
    Moss: No, we're just.
    Aaronow: We're just "talking" about it.
    Moss: We're just speaking about it. (Pause.) As an idea.
    Aaronow: As an idea.
    Moss: Yes.
    Aaronow: We're not actually talking about it.
    Moss: No.
    Aaronow: Talking about it as a.
    Moss: No.
    Aaronow: As a robbery.
    Moss: As a "robbery"?! No.
  • Site Rules Amendment Regarding ChatGPT and Sourcing
    ↪fdrake


    I've been thinking of beginning all my replies with "That's a very interesting point! I would enjoy the opportunity to explore these ideas further with you."

    Is that likely to be a problem?
Home » Srap Tasmaner