Comments
-
Was I wrong to suggest there is no "objective" meaning in life on this thread?A way to resolve the PSR problem is to give a sufficient reason for the existence of humans and the universe, and there is nothing to require that the reason be a cause. The reason could be a purpose — Hanover
This makes no sense.
"Humans exist because Martians intend to use us as food" is a non sequitur, whereas "humans exist because Martians created Adam and Eve in a lab and set them loose on Earth" isn't.
I think your reasoning stems from the fact that the word "reason" can be used to refer to both the "how" (e.g. "Martians created us in a lab") and the "why" (in the sense of motivation, e.g. "Martians intend to use us as food"), but to equate the two is to equivocate. -
Was I wrong to suggest there is no "objective" meaning in life on this thread?Would you agree that if it were an absolute fact humanity simply evolved organically over millions of years, and the modern human is the most advanced and intelligent being in this and any universe, human life has in fact no real purpose? — Outlander
Well, yes, that's what I've been saying from the start.
Given the definition of the word "purpose", to say that "human life has no purpose" is just to say that "nothing and nobody is using human life to achieve some intended outcome". -
Hate speech - a rhetorical pickaxeMore often than not, hate speech incites violence on the one who speaks it. It’s why police defend the KKK and the American Nazi party to hold their rally’s and marches, in order to protect them from violence — NOS4A2
So incitement is possible? Glad you came around in the end. -
Was I wrong to suggest there is no "objective" meaning in life on this thread?And, probably most importantly, your comment is a statement of a worldview, which might just be a foundational disagreement. I think many do believe the opposite, as in "There must be a purpose, but there might not be a cause." This is consistent with a theological position, arguing from positions of eternity, creation ex nihlio, and ultimate purpose. — Hanover
I was really just referring to cause and purpose in the context of human life. Humans haven’t always existed, and nor did we spontaneously and without cause come into existence at some point in the past.
My point is just that there is a semantic difference between the phrases “the origin of human life” and “the purpose of human life”. The former refers to the manner in which human life came into existence (and there must be an explanation of some kind) and the latter refers to the outcome that human life is intended to achieve (and there might not be such a thing). -
Was I wrong to suggest there is no "objective" meaning in life on this thread?There's always a purpose. Be it simple, as a mental invalid wishing to express whatever their decrepit brain desires, or not. I feel you mean, there's not always a "goal" or aspect and dynamic of "intelligent reasoning" that can distinguish between past (knowledge), present (circumstance), and outcome (vision). Perhaps that's what you mean. — Outlander
In context the phrase “the purpose of life” doesn’t mean “what I want to do with my life”.
It’s implicitly “the purpose of all human life”, and suggests that humanity exists to achieve the intended outcome of some “higher” power, whether that power be Yahweh, the Hindu pantheon, or the Engineers from the Prometheus movie. -
Was I wrong to suggest there is no "objective" meaning in life on this thread?That is, the flip side of the coin of "asking for the "purpose" of life is asking for the outcome that the existence of life is intended to achieve" is "asking for the "cause" of life is asking for the origin that the existence of life is supposed to have originated from." — Hanover
“Cause” and “purpose” mean different things. There must be a cause but there might not be a purpose. -
Free Speech - Absolutist VS Restrictive? (Poll included)I don’t abhor speaking. — NOS4A2
You abhor government censorship.
The President and the chair of the FCC using their words to threaten their critics into not saying the things they're saying and/or to have them deplatformed under the pretence of legal responsibility is government censorship, even if not said face-to-face, officially and formally. It isn't just them casually speaking their mind. No reasonable person accepts "will no one rid me of this troublesome priest?" as plausible deniability. You're engaging in poor apologetics, plain and simple. -
Free Speech - Absolutist VS Restrictive? (Poll included)Right, but when the EU commission directly threatens Elon Musk with fines it’s just “Reminding someone of their legal obligations to moderate their platform”. — NOS4A2
Yes, because that's what he was doing. Whereas Carr and Trump are using transparently tenuous and bullshit justifications to attack their critics. Everyone other than absurd apologists like you can see it for what it is.
I don’t believe that at all. — NOS4A2
I don't know what you believe, but what you said in earlier posts was a defence of Carr's and Trump's words, pretending that they weren't doing the very thing that you claim to abhor. -
Was I wrong to suggest there is no "objective" meaning in life on this thread?Purpose is an intended outcome. Asking for the "purpose" of life is asking for the outcome that the existence of life is intended to achieve. That requires that someone or something with intentions created and/or is using life to achieve that outcome, e.g. one or more gods perhaps.
Personally, I'd prefer it if my life wasn't being used by someone or something else as pawn in whatever game they're playing. I decide for myself what to do with my time here. -
Free Speech - Absolutist VS Restrictive? (Poll included)For someone so defensive of government censorship and speech regulation, though, you’re suddenly so adamant about free speech. — NOS4A2
Your (apparently faux) commitment to free speech absolutism has left you incapable of understanding nuance and that the real world isn't black and white.
That I disagree with your claim that all speech regulation is bad isn't that I believe that all speech regulation is good.
Laws against defamation, conspiracy, and incitement to violence are both prudent and justified. The government and the President threatening to revoke the licenses of news organisations that are critical of them is bad.
It's ironic that your obsession to defend Trump even leads you to turn a blind eye to blatant, unjustified, government censorship, trying to whitewash it away as being something other than what it is. Even Ted Cruz and other Republicans are calling it out. This isn't just some liberal, anti-Trump hysteria.
Their licenses forbid them from spreading lies like Kimmel did and must consider the public interest. — NOS4A2
And what lie is that? All he said was "the MAGA gang are desperately trying to characterise this kid who murdered Charlie Kirk as anything other than one of them and doing everything they can to score political points from it" (and then mocked Trump for responding to a question about Kirk by bragging about the new White House ballroom).
It's laughable if you think that something so insignificant, even if false, warrants revoking a news organisation's license. Compare that with basically the entirety of Fox News, which even has hosts suggesting that homeless people should be murdered. Silence from Trump, Carr, and the FCC. -
Free Speech - Absolutist VS Restrictive? (Poll included)
Reminding someone of their legal obligations to moderate their platform is not the same as threatening to revoke a network's license if they don't fire someone who mocked Trump's response to a question about Kirk and who insinuated that the shooter was a conservative, which is all Kimmel did.
And Trump very explicitly said that he wanted to revoke the licenses of networks who are negative of him. There's no legal requirement to kiss his ass or to lie and pretend that he's doing a good job.
For someone who is so in favour of free speech absolutism and critical of government overreach, you sure are doing your best to bend over backwards and pretend that nothing problematic is happening. -
Free Speech - Absolutist VS Restrictive? (Poll included)I think right now the only thing that stand between us and dictatorship is the courts. — frank
Have you been paying attention to the same courts I have? :sweat: -
Free Speech - Absolutist VS Restrictive? (Poll included)Subtext. Yet there were no conversations between either of the parties you mention. — NOS4A2
Yes. When the FCC publicly threatens to revoke a network's license unless they penalize an employee, that is a threat even if not said in person to that network. You are being incredibly dense.
Perhaps it is the case that Newstar and Sinclair group didn’t want to show the episode because they didn’t like it, just as they said. — NOS4A2
But they did show it. And then they fired him after the backlash, which notably included the FCC chair threatening to revoke their license.
Are you just going to dismiss this as lies? — NOS4A2
Yes, I think they're lying. But even if they're telling the truth, it is still the case that the FCC was threatening to revoke their license, with the President supporting this threat and threatening to have the license of more of his critics revoked. These two things are not mutually exclusive. -
Free Speech - Absolutist VS Restrictive? (Poll included)Oh, that’s right, Trump talking is government pressure in some circles. Forgive me. — NOS4A2
Yes. As is this.
The FCC is signaling potential immediate action against Jimmy Kimmel, ABC, and parent company Disney, with Chairman Brendan Carr blasting what he calls “malicious lies” about the murder of Charlie Kirk. Carr said the late-night host deliberately misled viewers by claiming Kirk’s assassin was a MAGA Conservative, calling the statement “truly sick.”
Carr made clear the FCC has a “strong case” to hold Kimmel, ABC, and Disney accountable for spreading what he described as dangerous, politically motivated misinformation.
He suggested penalties could range from Kimmel’s suspension to ABC facing scrutiny of its broadcast license.
“This is a very, very serious issue right now for Disney,” Carr said during an appearance with podcaster Benny Johnson. “We can do this the easy way or the hard way. These companies can find ways to take action on Kimmel, or there is going to be additional work for the FCC ahead.”
Brendan Carr emphasized that ABC and its affiliates must meet obligations tied to their licenses. “They have a license granted by us at the FCC, and that comes with it an obligation to operate in the public interest,” he said.
Calls for Kimmel’s firing have circulated in recent days, but Carr stopped short of demanding termination. “I think you could certainly see a path forward for suspension over this,” he noted, adding that the Commission could argue Kimmel’s remarks were “an intentional effort to mislead the American people about a very core fundamental fact.”
If you think that only direct, explicit, face-to-face demands count as pressure or threats then you might have autism. The rest of us understand subtext. -
Free Speech - Absolutist VS Restrictive? (Poll included)Nexstar media group said they made the decision to stop showing Kimmel unilaterally, without discussion with the government. They had the betterment of their audience in mind. I’m afraid they also have the free speech right to broadcast whatever they wish. — NOS4A2
I didn't mention Kimmel. I was alluding to this:
Speaking on Thursday to reporters aboard Air Force One, Trump said, “I have read someplace that the networks were 97% against me, again, 97% negative, and yet I won and easily, all seven swing states,” referring to his 2024 election win.
“They give me only bad publicity, press. I mean, they’re getting a license,” Trump said, according to audio from a press gaggle provided by the White House.
“I would think maybe their license should be taken away,” Trump said.
The president said that the decision “will be up to Brendan Carr.”
Trump specifically referred to criticism he has gotten from Kimmel and CBS late-night talk-show host Stephen Colbert.
“Look, that’s something that should be talked about for licensing, too,” Trump said.
“When you have a network and you have evening shows, and all they do is hit Trump,” he said. “That’s all they do. If you go back, I guess they haven’t had a conservative on in years or something, somebody said.”
“But when you go back, take a look, all they do is hit Trump. They’re licensed. They’re not allowed to do that. They’re an arm of the Democrat party,” he said. -
Free Speech - Absolutist VS Restrictive? (Poll included)
But this isn’t “cancel culture”. This is government pressure.
The general public are well within their rights to “demand” that someone be fired, and threaten a boycott otherwise, because the general public are under no obligation to buy some business’s goods or services. That’s a legitimate expression of free speech.
But the president and government agencies threatening to revoke their critics’ licenses is a different matter entirely. -
Free Speech - Absolutist VS Restrictive? (Poll included)
There’s a difference between “cancel culture”, i.e boycotts, and government pressure to fire critics. -
Free Speech - Absolutist VS Restrictive? (Poll included)Voluntary or not, the thing that does the action is operating under its own power... — NOS4A2
Okay, but the claim I responded to was: "this is another instance of everything being willed by yours truly."
My heartbeat is involuntary, and so therefore isn't "being willed by yours truly". Transduction is involuntary, and so therefore isn't "being willed by yours truly". -
What is real? How do we know what is real?
Okay, but it’s not about the real you. It’s about a version of you who’s only ever lived inside a windowless room and so has never seen what happens outside. Something enters the room. Are you able to determine whether or not that thing existed before it entered? Are you able to determine whether or not that thing will continue to exist after it leaves? Are you able to determine what it was or will be doing outside? -
What is real? How do we know what is real?If it is, say, a fly in the room, it is unlikely to change much outside the room. If it is a chrysalis or a caterpillar, it will likely be very different outside the room. — Ludwig V
On what grounds can you justify the likeliness of something changing outside the room if you've never been outside the room? -
What is real? How do we know what is real?It seems that you do know what kind of thing the something is while it is in the room. That will give you a basis for working out what existence it has outside the room. — Ludwig V
All I can do is assume. But perhaps it looks and behaves very different when outside the room. It’s impossible for me to know. -
Hate speech - a rhetorical pickaxeWhat is the real definition of hate speech? — Roke
https://dictionary.cambridge.org/us/dictionary/english/hate-speech
public speech that expresses hate or encourages violence toward a person or group based on something such as race, religion, sex, or sexual orientation -
A -> not-ARight. — NotAristotle
Which doesn't make any sense. C1 is false if and only if both "I am a man" is false and "pigs can fly" is false. Yet by stipulation "I am a man" is true; that's P1.
So, as per the rules of logic, if both P1 and P2 are true then C1 is true. The inference is valid. -
A -> not-AI think P2 excludes the possibility of the C1 disjunctive introduction and therefore foils the entire argument. — NotAristotle
If P1 is true then C1 is true. Therefore, the inference is valid.
You seem to be suggesting that if both P1 and P2 are true then it's possible that C1 is false? -
A -> not-AI see no inference rules being applied in an explosion hypothesis and therefore cannot see it as a deduction at all. — NotAristotle
I explained it above.
P1. I am man
C1. Therefore, either I am a man or pigs can fly (from P1, using disjunction introduction)
P2. I am not a man
C2. Therefore, pigs can fly (from C1 and P2, using disjunctive syllogism) -
What is real? How do we know what is real?I'm afraid I'm somewhat handicapped here, in that I don't really understand what reality-in-itself is. — Ludwig V
As an analogy, let’s assume that I’m trapped in a windowless room. Something enters the room. I can see that it exists and what it looks like and how it behaves now that it’s in the room, but I don’t know that it existed or what it looked liked or how it behaved before it entered the room (or after it leaves); perhaps it’s very different (or doesn’t exist) when not in the room.
In this case “being in the room” is an analogy for “being seen”. -
A -> not-AI get what you are saying. However, I maintain that it is strange for me to think of the initial argument of this thread as "valid." — NotAristotle
What do you think "valid" means? It just means that the conclusion can be deduced from the premises using the rules of inference. It doesn't mean that the argument is sound or cogent.
but the principle of explosion is also nonsensical to me. — NotAristotle
1. Either I am a man or pigs can fly
(1) is true if either "I am a man" is true or "pigs can fly" is true. Therefore, we can deduce (1) from the premise "I am a man". This is called disjunction introduction:
P1. I am a man
C1. Therefore, either I am a man or pigs can fly
Separately, we can deduce that if (1) is true and "I am a man" is false then "pigs can fly" is true. This is called disjunctive syllogism:
P1. Either I am a man or pigs can fly
P2. I am not a man
C1. Therefore, pigs can fly
So what happens when we combine the two?
P1. I am man
C1. Therefore, either I am a man or pigs can fly (from P1)
P2. I am not a man
C2. Therefore, pigs can fly (from C1 and P2)
From the contradictory premises "I am a man" and "I am not a man" we have deduced the conclusion "pigs can fly". We can deduce anything from a contradiction. This is part of the reason why we agree that contradictions are impossible. -
Consciousness and eventsFrom what I vaguely understand, the idea is that the wave-function is a universal wave-function, i.e that the universe as a whole is in a superposition, not just the cat, so there is a universe in which the cat is alive and a universe in which the cat is dead. So any physical measuring device is also in a superposition and cannot act as an "outside observer" capable of collapsing the universal wave-function; only something that is not a part of the universal wave-function can do that. The (non-physical) mind is the presumptive candidate.
The alternative view is that the universal wave-function doesn’t collapse and so both universes are real, leading to the many-worlds interpretation.
Or superposition is epistemic, not ontological, leading to de Broglie-Bohm theory. -
Consciousness and events
-
The American Gun Control Debate
I don’t understand what you’re trying to argue. If it’s just that my likelihood of surviving a knife attack is greater if I have a gun than if I’m unarmed, then I agree, but it’s incredibly myopic and naive to think that this proves anything.
You need to look at the bigger picture; at what actually happens in the real world.
The epidemiology of self-defense gun use: Evidence from the National Crime Victimization Surveys 2007–2011
Self-defense gun use (SDGU) occurs in fewer than 1% of contact crimes.
...
SDGU is not associated with a reduced risk of victim injury.
...
Of over 14,000 incidents in which the victim was present, 127 (0.9%) involved a SDGU. SDGU was more common among males, in rural areas, away from home, against male offenders and against offenders with a gun. After any protective action, 4.2% of victims were injured; after SDGU, 4.1% of victims were injured. In property crimes, 55.9% of victims who took protective action lost property, 38.5 of SDGU victims lost property, and 34.9% of victims who used a weapon other than a gun lost property.
...
Compared to other protective actions, the National Crime Victimization Surveys provide little evidence that SDGU is uniquely beneficial in reducing the likelihood of injury or property loss.
Then consider the high levels of gun violence more generally that come with high levels of gun ownership. There are so many mass shootings, school shootings, and other gun homicides in the USA. Yet somehow their citizens are safer because they have a gun that they can putatively use in self-defence?
It seems like their defence of gun ownership is a fantasy that contradicts the actual facts.
I'll stick to what the statistics and studies show. My country is safer with strict gun control, and so I'm glad that we have it. -
The American Gun Control DebateUnfortunately, if someone is out to seriously hurt you, they will have considered it as well. — Tzeentch
And as I said before, if someone is out to seriously hurt me then I’d rather neither of us have guns than both of us have guns.
I’m unlikely to be sniped to death with a knife from 200 yards whilst I’m busy debating college students. -
The American Gun Control DebateI'm talking about fending off a knife fighter and you only have your bare fists. — Tzeentch
Running away is perhaps the most effective option.
Also, I agree that wars would be less deadly without guns - they would be less deadly for the side made up of criminals fighting against the side made up of law-abiding, normal people.
It would be a landslide for the criminals. — Tzeentch
I don't understand what you're trying to say here. -
The American Gun Control DebateYou know what, maybe they are not effective, but they're a hell of a lot more effective than your bare fists I'll tell you that much. — Tzeentch
I'm much more likely to survive a fist fight than a gun fight. -
The American Gun Control Debate
Comparing street crime to warfare is a false equivalency. But that said, I'm 100% certain that wars would be less deadly without guns (and other long-range weaponry). -
The American Gun Control DebateAnd I would much rather have "the great equalizer" as ↪Outlander called it. — Tzeentch
Perhaps if we have a pistols-at-dawn duel, but that's not the reality. It's drive-by shootings, someone pulling a gun on you before you know what's happening, being shot at a distance and from behind, etc.
And according to this, "overwhelming evidence demonstrat[es] that firearms are not an effective means of self-defense." -
The American Gun Control DebateUK and many other countries in Europe including my own are turning into shitholes. The sense of safety that once was is now just an illusion. People feel safe because they had the good fortune not to be confronted with reality, which is that if they cross paths with the wrong people the authorities can't and won't do a single thing. — Tzeentch
Also see this:
Seventy-eight per cent of people in England and Wales think that crime has gone up in the last few years, according to the latest survey. But the data on actual crime shows the exact opposite.
As of 2024, violence, burglary and car crime have been declining for 30 years and by close to 90%, according to the Crime Survey for England and Wales (CSEW) – our best indicator of true crime levels. Unlike police data, the CSEW is not subject to variations in reporting and recording.
The drop in violence includes domestic violence and other violence against women. Anti-social behaviour has similarly declined. While increased fraud and computer misuse now make up half of crime, this mainly reflects how far the rates of other crimes have fallen.
All high-income countries have experienced similar trends, and there is scientific consensus that the decline in crime is a real phenomenon. -
The American Gun Control DebateI think you had to delete what you wrote because you could be arrested for it. I couldn’t imagine. — NOS4A2
I deleted it because in my haste I was putting words in your mouth, which may have been unwarranted. Perhaps you weren't referring to government tyranny but crime, like Tzeentch above. -
The American Gun Control Debate
If this is a reference to criminals then I'll repeat what I said to NOS4A2 before: I’d much prefer it if they don’t have access to guns, even if that means I don’t have access to guns either. -
The American Gun Control DebateMany Americans see what is happening to the UK and it only reaffirms the reasons we should never give up our guns. — NOS4A2
What things? -
A -> not-AIn what world is "1 and 2 therefore not 1. 1 and 2. Therefore, not 1." a sensible or logical maneuver? It most certainly is not modus ponens so understood. — NotAristotle
The bottom line shows modus ponens. It doesn't matter what A and B mean:
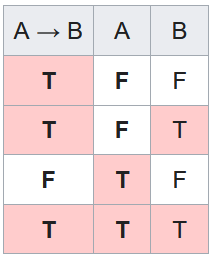
Now replace B with ¬A. Only one line has both A → ¬A and A true, and on that line ¬A is also true. That's all it means for the argument to be valid.
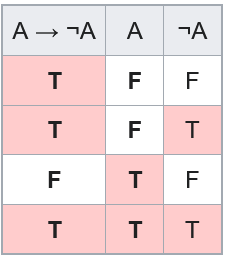
However, two of the lines are removed by the laws of excluded middle (the top) and non-contradiction (the bottom)
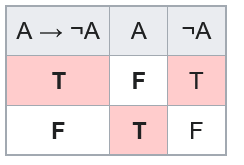
That gives us:
A → ¬A
∴ ¬A
Or
A
∴ ¬(A → ¬A)
So the argument is unsound.
Michael

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum


