-
Is indirect realism self undermining?Upon the completion of the experiment, an indirect realist walks in to see the results. They are not sure what to think. Surely, they thought that even though they are reporting the community accepted color word for each object correctly, they must be having different a “experience” of color since different neuron cluster are lighting up for each individual...........The indirect realist has no way of knowing which color individual A or B is having in any of these “private experiences” of color based on these results. But how could they ever make sense of these results since there is no private language we could use to understand anyway of what is going on inside their “heads.” As Wittgenstein says in PI 293, “That is to say: if we construe the grammar of the expression of sensation on the model of ‘object and designation’ the object drops out of consideration as irrelevant.” — Richard B
Your post lays out my position as an Indirect Realist.
1) The Indirect Realist doesn't need a private language to have the private experience of a colour.
There are many things I see that I don't have a word for. This doesn't stop me from seeing them.
2) Wittgenstein's PI 293 is a good explanation why Indirect Realism is a workable theory.
PI 293 explains how there can be a public language even though each person's private experiences may be unknown to anyone else. -
Is indirect realism self undermining?I would argue that the word "grue" refers to their private experiences, which are different, despite the shared public use. — Michael
I agree, Indirect Realism is a workable theory. -
Is indirect realism self undermining?Don't you mean to say that Wittgenstein's beetle in the box analogy justifies talk of indirect realism in relation to the third-personal public concept of perception, but that this doesn't justify talk of indirect-realism in the case of one's own perception? — sime
From the third-person, Wittgenstein's beetle in the box analogy shows that Bill and Bob can carry on a conversation even if they don't know what is in each other's mind. From the first-person, I could be Bill, and still be able to carry on a conversation with Bob.
consider the irrealist understanding of the beetle on the box — sime
Other than a general estrangement from our generally accepted sense of reality, I don't know Goodman's theory.
Given that each individual only has access to his or her private colour, and uses his or her mother-tongue in a bespoke private fashion when referring to the "shared" circle, then what is the purpose of colouring in the shared circle? — sime
I agree, henceforth I will remove the colour from the circle.
Following this line of thought further, one could even deny the very existence of a shared circle, as part of a strategy for defending direct-realism for all perceivers — sime
I agree, as my belief is in neutral monism, where in a mind-independent world there are only elementary particles, elementary forces and space-time. In a mind-independent world there are only parts and no wholes such as circles, trees, colours, etc. -
Is indirect realism self undermining?Better yet, to be consistent with Wittgenstein's view of “private language” one should remove the colors inside the heads of the figures. — Richard B
Wittgenstein p 293 PI
Suppose everyone had a box with something in it: we call it a "beetle". No one can look into anyone else's box, and everyone says he knows what a beetle is only by looking at his beetle.—Here it would be quite possible for everyone to have something different in his box.
Wittgenstein writes that everyone says there is something in their head, even if no one else knows what it is, so I cannot leave Bills' head blank. It may be the colour yellow, but it may not. -
Is indirect realism self undermining?to be consistent with indirect realism and to prevent any real-world bias, it would be best not to colour the circle in the middle — Michael
I agree that not colouring the circle would be more consistent with Direct Realism.
the same kind of light will trigger the same kind of experience — Michael
Yes, in practice this must be the case, as Bill and Bob are the product of the same 3.5 billion years of evolution, they share 99.9 % of their genetic makeup and they share the same common ancestor, Mitochondrial Eve.
Knowing these facts, Bill and Bob will agree they most likely have had the same private experience and therefore can sensibly name it "grue". -
Is indirect realism self undermining?The private language argument is that such a thing cannot be understood in a coherent fashion. That there can be no private languages. That such a thing could not count as a language. — Banno
I agree.
===============================================================================
When the indirect realist says "I see the Earth", they are referring to the brown thing. When the direct realist says "I see the Earth", they are referring to the Earth. — Banno
This is misleading wording. To say that the Direct Realist is referring to the Earth is pre-judging that the Direct Realist is in fact correct in their belief that they are referring to the Earth.
Better wording would be: When the indirect realist says "I see the Earth" they believe they are directly seeing a representation of the Earth. When the direct realist says "I see the Earth", they believe they are directly seeing the Earth.
The question is, who is right.
===============================================================================
Summarising, what the private language argument shows is that one cannot construct a private language that is about one's private sensations. If indirect realism holds that what we see is not the world but a private model of the world, then one could not construct a language about that private model. — Banno
Indirect Realism doesn't need to construct a private language about one's private sensations. I can have the private sensation of a colour without the necessity of having to describe it in words, or of having a private language.
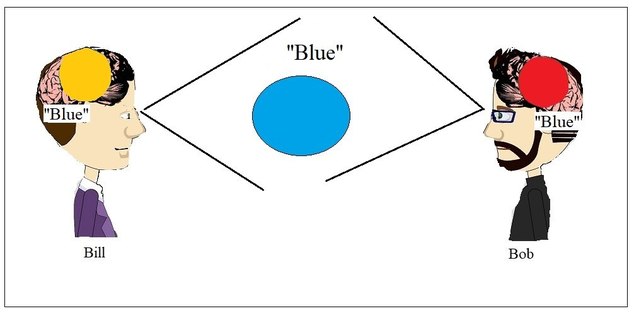
For example, the colour blue has been named "Blue" in a public performative act in the English language, and both Bill and Bob know this.
Note that the public word "blue" and the public colour blue are both objects in the world. For clarity, using the use-mention distinction, the blue in the object "blue" is a "mention", whilst the blue in the object with the colour blue is a "use".
It may be that when looking at the public colour blue, Bill has the private experience of yellow and Bob has the private experience of red, but both Bill and Bob have linked their private experience with the public word "blue", thereby allowing them to talk about objects in their shared world.
For example, if Bill asks Bob to pass over the "blue" object, even though Bill has the private experience of yellow and Bob has the private experience of red, Bob will successfully pass over the object Bill intends.
Indirect Realists can engage in a public social language without needing to be able to describe their private sensations.
Wittgenstein in para 293 in PI describes how everyone's private sensations may be different:
If I say of myself that it is only from my own case that I know what the word "pain" means—must I not say the same of other people too? And how can I generalize the one case so irresponsibly? Now someone tells me that he knows what pain is only from his own case!——Suppose everyone had a box with something in it: we call it a "beetle". No one can look into anyone else's box, and everyone says he knows what a beetle is only by looking at his beetle.—Here it would be quite possible for everyone to have something different in his box.
Wittgenstein continues that the private sensation has no place in a public language, and even if we do use the word "pain" in a public language it doesn't explain the sensation, only indicate that there is some kind of sensation
One might even imagine such a thing constantly changing.—But suppose the word "beetle" had a use in these people's language?—If so it would not be used as the name of a thing. The thing in the box has no place in the language-game at all; not even as a something: for the box might even be empty.—No, one can 'divide through' by the thing in the box; it cancels out, whatever it is.
Wittgenstein continues that the private sensation drops out of consideration within a public social language.
That is to say: if we construe the grammar of the expression of sensation on the model of 'object and designation' the object drops out of consideration as irrelevant.
===============================================================================
Treating this as a reductio, we do have language about the world, and therefore we talk about the world, and not about our private world-models. At least that form of indirect realism is wrong. — Banno
Indirect Realism accepts they have private sensations, but as argued by Wittgenstein in his beetle in the box analogy, such private sensations drop out of consideration within a public social language as irrelevant.
Wittgenstein's beetle in the box analogy justifies Indirect Realism.Attachment Realism 2
(54K)
Realism 2
(54K)

-
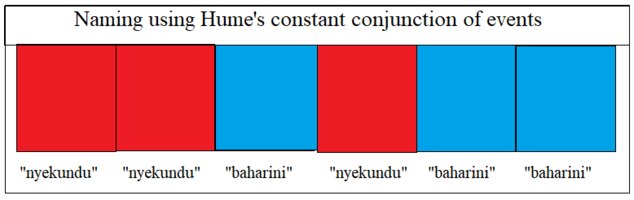
Is indirect realism self undermining?"Ngoe" means at least a third of the picture is green? Or the picture is an odd number from the left? — Banno
Good first attempt. We are on the path to successful communication, definitely an iterative process. It's a bit like the Twenty Questions parlour game using deductive reasoning and creative thinking.
I will have to come up with five more pictures that excludes at least a third of the picture of the "ngoe" being green and excludes "ngoe" being an odd number.
As Wittgenstein said in para 32 of PI:
"Someone coming into a strange country will sometimes learn the language of the inhabitants from ostensive definitions that they give him; and he will often have to guess the meaning of these definitions; and will guess sometimes right, sometimes wrong." -
Is indirect realism self undermining?An illiterate deaf mute with no language can see a tree "in their mind". They just won't call it "tree"...I've seen many animals that I don't have a name for...But perception doesn't depend on meaning — Michael
I agree, perception doesn't depend on meaning. There is an asymmetry between meaning and perception. -
Is indirect realism self undermining?You need to read up on the use-mention distinction. — Michael
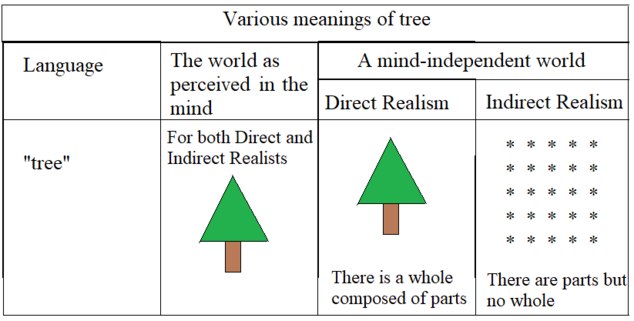
Both the Indirect and Direct Realist directly perceive a tree in their minds. For both the Indirect and Direct Realist, the tree they perceive exists in the world. Note that Wittgenstein in Tractatus didn't specify where this world existed.
Example of "the tree is green" is true IFF the tree is green
"The tree is green" being in quotation marks is within language. The tree is green not being in quotation marks is in the world.
For the Indirect Realist, the world in which the tree exists is in their mind. For the Direct Realist, the world in which the tree exists is in a mind-independent world.
The meaning of the word "tree" has nothing to do with perception — Michael
If that were true, you would know the meaning of the word "mlima" even if you had never perceived one.
You could argue that even if you have never perceived a "mlima", it could be described to you, such that a "mlima" consists of "mwamba" and "theluji". But this doesn't solve the problem, in that you you cannot know the meaning of either "mwamba" or "theluji" until having perceived them. Sooner or later, meaning depends on perception. In Bertrand Russell's terms, knowledge by acquaintance.Attachment Realism
(11K)
Realism
(11K)
-
Is indirect realism self undermining?Who told you what the name of the effect was? — Isaac

In a sense, no one needs to tell me the name of the image that I perceive. I would assume that just from five pictures you could hazard at a guess at the meaning of "ngoe". I discover the name from a constant conjunction of events. -
Is indirect realism self undermining?This is a misreading of the private language argument. — Banno
My proposal is that Wittgenstein's Philosophical Investigations does not support Direct Realism.
Direct Realism argues that we perceive objects in the world as they really are, immediately and directly.
If Direct Realism is true, one person's private experience of something in the world, such as a tree, will be the same as another person's private experience of the same tree, meaning that each person will know the other person's private experiences.
Wittgenstein argues that nobody can know another person's private experiences
In para 272 of PI, Wittgenstein writes that nobody can know another person's private experiences:
"The essential thing about private experience is really not that each person possesses his own exemplar, but that nobody knows whether other people also have this or something else. The assumption would thus be possible—though unverifiable—that one section of mankind had one sensation of red and another section another."
The Private language argument prevents talking about or discussing the pros and cons of Indirect and Direct Realism
There is an excellent and informative article in Wikipedia, the Private language argument that I always refer to.
The Wikipedia article Private language argument notes that the private language argument argues that a language understandable by only a single individual is incoherent, from which it follows that there is no language that can talk about or describe inner and private experiences.
1) The private language argument argues that a language understandable by only a single individual is incoherent,
2) If the idea of a private language is inconsistent, then a logical conclusion would be that all language serves a social function.
3) For example, if one cannot have a private language, it might not make any sense to talk of private experiences or of private mental states.
4) In order to count as a private language in Wittgenstein's sense, it must be in principle incapable of translation into an ordinary language – if for example it were to describe those inner experiences supposed to be inaccessible to others
Direct Realism is the position that our inner experience of an object in the world is direct and immediate. Indirect Realism is the position that we cannot know whether or not our inner experience of an object in the world is direct and immediate.
As Wittgenstein's private language argument argues that no language can talk about or describe inner and private experiences, it follows that the pros and cons of Indirect and Direct Realism is not something that can be talked about or described.
Summary
On the one hand, Wittgenstein's private language argument prevents discussion of Indirect and Direct Realism, but on the other hand, Wittgenstein writes that nobody can know another person's private experiences. That nobody can know another person's private experiences is at odds with the consequences of Direct Realism. -
Is indirect realism self undermining?In the absence of any English speaker the word "tree" wouldn't exist, but the object currently referred to by the word "tree" would exist. — Michael
Exactly, that is what an Indirect Realist would say. The Direct Realist would have said "In the absence of any English speaker, the word "tree" wouldn't exist, but the tree would still exist in the world"
There's a very peculiar obsession with language in this discussion — Michael
As I believe in the ontology of Neutral Monism, where reality consists of elementary particles and elementary forces in space-time, the meaning of the word tree is fundamental to my philosophical understanding. -
Is indirect realism self undermining?What could we call that thing...? If only there was a word for the thing in the world which I can make furniture out of, climb, get fruit from, paint the image of, sit under the shade of........ We really need a word for thing.......I suggest "tree(a)", what with the word "tree" already having been taken and all. — Isaac
This is the slightly mad bit.......That 'something that has caused me to perceive a "tree'?...........It's a tree........That's what a tree is. — Banno
Yes, "tree" is a good word. Within our language game we have the word "tree".
However, in the absence of any English speaker, the word "tree" would not exist, and "trees" would not exist in the world. In the absence of any English speakers, no one could discover in the world "trees". "Trees" only exist in the minds of speakers of the English language.
I perceive something that has been named "tree". As "trees" only exist in the mind, I am perceiving something in my mind that only exists in my mind, leading to a self-referential circularity.
This is the flaw in Searle's solution of the "intentionality of perception" to the epistemological problem of how we can gain knowledge of objects in the real world from private sense data, in that his solution leads to a similar self-referential circularity.
As an Indirect Realist I directly see a tree, I don't see a model of a tree. Searle wrote "The experience of pain does not have pain as an object because the experience of pain is identical with the pain". Similarly, the experience of seeing a tree does not have a tree as an object because the experience of seeing a tree is identical with the tree.
I have an innate belief in the law of causation, in that for every effect there is a cause, as well as the belief that the cause of an effect cannot be known just from knowing the effect. Combining these, my perceiving a "tree" must have been caused by something, yet I cannot know just from my perception what caused it.

Yet I need a name for the cause of my perception of a tree. My solution is to give the cause the same name as the effect. Therefore, if I see the colour green, I name its cause green. If I hear a grating noise, I name its cause a grating noise. If I smell an acrid smell, I name its cause an acrid smell. If I feel something silky, I name its cause silky. If I taste something bitter, I name its cause bitter. If I perceive a tree, I name its cause a tree.
"Trees" only exist within the language game. "Trees" exist within the mind as not only the name for what is perceived by the mind but also as the name of the unknown cause of that perception, ie "a tree" is the cause of perceiving "a tree". -
Is indirect realism self undermining?If this is true, it's not a discovery about seeing but only about the grammar of 'see.' — green flag
Yes, which shows the importance of Wittgenstein's discussion of the language game in Philosophical Investigations. -
Is indirect realism self undermining?I can build furniture out of fallen trees. Can I build furniture out of what you see in your dreams and hallucinations? — Isaac
You can build furniture out of the something in the world that has caused me to perceive a tree providing this had been a veridical experience, but not if a dream or an hallucination.
How could one ever be mistaken about what one sees? — Isaac
One can never be mistaken about what one sees. If you see a tree, it is absolutely certain that you have seen a tree. If you see a unicorn running through Central Park, it is absolutely certain you have seen a unicorn running through Central Park.
However, one can be mistaken in one's belief whether it was a veridical experience, a dream, an illusion, a film or an hallucination. -
Is indirect realism self undermining?But can they see trees? — Isaac
According to Do blind people dream in visual images?, yes.
Instead, scientists have performed brain scans of people blind since birth while they are sleeping. What scientists have found is that these people have the same type of vision-related electrical activity in the brain during sleep as people with normal eyesight. Furthermore, people blind since birth move their eyes while asleep in a way that is coordinated with the vision-related electrical activity in the brain, just like people with normal eyesight. Therefore, it is highly likely that people blind since birth do indeed experience visual sensations while sleeping. They just don't know how to describe the sensations or even conceptually connect in any way these sensations with what sighted people describe as vision. -
Is indirect realism self undermining?What about the tree that you climb? Is that a representation? — unenlightened
I know that I perceive something and I know that this something has the name "tree".
As I innately believe in the law of causation, in that every effect has a cause, I therefore believe that there is something that has caused me to perceive a "tree". I don't know what this something is, but I do believe it exists.
As language doesn't exist in the absence of sentient beings, the something in the world that we call a "tree" cannot be a "tree", as "trees" only exist within human language. "Tree" as a word in human language represents something else.
Therefore the "tree" that I climb as a word is a representation of something else but the something else that has caused me to perceive a "tree" isn't a representation. -
Is indirect realism self undermining?So, for you, the eyes are not involved in seeing. A blind man can see? — Isaac
I see what you mean. I see the reason for your post. I see the relation between the eyes and what is seen. I see trees in my dreams. A fool cannot see beyond the end of their nose. I see trees in my hallucinations. I see myself on holiday. I see the light at the end of the tunnel. A blind man can see the truth. A blind man can see where they went wrong. A blind man can see the error of their ways.
Yes, a blind man can see. -
Is indirect realism self undermining?But for indirect realism, what everyone sees is some private mental image, and hence what you see and what the other person sees are quite different. — Banno
Almost, in that my private perception of a tree may or may not be the same as anyone else's, but it is impossible to know, as it is a private mental image.
Wittgenstein Philosophical Investigations may be used to give insights into Indirect Realism, including his strong case against the possibility of a private language and his arguing that nobody knows another person's private sensations.
The Indirect realist accepts Wittgenstein's conclusion that one's private perception of an object, such as a tree, is forever unknown to anyone else.
The Direct Realist doesn't accept Wittgenstein's conclusion. The Direct Realist argues that we perceive objects in the world as they really are, immediately and directly. Therefore, if two people are looking at the same object in the world, such as a tree, as both will be perceiving the same object in the world immediately and directly, their private mental images will be the same, meaning that each will know the others private sensations.
Therefore, whether one is an Indirect or Direct Realist depends in part of whether one accepts Wittgenstein's Philosophical Investigations
If indirect realism were taken at face value, two people cannot both look at the same thing — Banno
Wittgenstein's para 293 in Philosophical Investigations about a beetle in a box provides a solution to the problem raised about Indirect Realism, ie, how is communication possible between people using a public language when nobody can know another person's private sensations.
For example, as an Indirect Realist, my private mental image of a tree may be different to everyone else's, yet I can use use the word "tree" in a social language game with others. Within the language game, the word "tree" isn't describing my mental image, as each particular mental image has dropped out of consideration within a language game as irrelevant.
Wittgenstein's beetle in the box explains the connection within Indirect Realism between private mental images and a public language.
The indirect realist says what one sees is the model of the tree — Banno
As an Indirect Realist, I am not saying that I see a model of a tree, I am saying that I directly see a tree, though the tree I see is an indirect representation, image or model of something that exists in the actual world.
A key concept is intentionality, in that my mind is directed at the tree that I perceive, not in virtue of the tree representing another object, another tree, as this would lead into an infinite regression and the homunculus problem. -
Is indirect realism self undermining?In terms of intentionality I'm talking to (and seeing) my parents, but given the physics and mechanics of external objects and light and sound and the central nervous system, the phenomenology of experience is indirect. — Michael
Yes, intentionality is closely associated with phenomenology.
Taken from the article What Is Intentionality, and Why Is It Important? by Robert Sokolowski:
"The term most closely associated with phenomenology is “intentionality.” The core doctrine in phenomenology is the teaching that every act of consciousness we perform, every experience that we have, is intentional: it is essentially “consciousness of” or an “experience of” something or other. All our awareness is directed toward objects. If I see, I see some visual object, such as a tree or a lake; if I imagine, my imagining presents an imaginary object, such as a car that I visualize coming down a road; if I am involved in remembering, I remember a past object; if I am engaged in judging, I intend a state of affairs or a fact. Every act of consciousness, every experience, is correlated with an object. Every intending has its intended object."
Intentionality is common to both Indirect and Direct Realists.
As an Indirect Realist, when I see a tree, there are two aspects. First, intellectually, I know that my mind is directed onto a representation of a tree. Second, viscerally, I know that my mind is directed onto a tree, not a representation of a tree.
After all, even as an Indirect Realist, if I was standing in the middle of the road and saw a truck approaching me, I wouldn't think "just a representation of a truck" and remain where I was. -
Is indirect realism self undermining?This is the exact red herring that is almost always brought up in the debate between direct and indirect realism. — Michael
I am sure that we both agree with Indirect Realism.
Searle definitely supports Direct Realism, and within Direct Realism, as also discussed by Pierre Le Morvan in his article Arguments against Direct Realism and how to counter them, there is causal indirectness (PDR) and cognitive indirectness (SDR).
I would assume Searle agrees with the cognitive indirectness version of Direct Realism, as he must well know the bent stick problem.
What do you mean by red herring ? -
Is indirect realism self undermining?Yeah, but what Searle is suggesting is not what you are criticising. — Banno
I think I am criticising what Searle is suggesting.
I don't agree with Searle in his support of naive realism (direct realism), as it seems to me that only Indirect Realism can satisfactorily explain how we interact with the world.
As Searle said "I think the rejection of naive realism was the single greatest disaster that happened in philosophy after Descartes...................but the idea that you can't ever perceive the real world but only a picture in your mind that creates a disaster, because the question that arises is what is the relationship between the idea you do perceive or the sense datum of the impression that you do perceive and the real world, and there is no answer to that which is satisfactory once you make once you make the decisive move of rejecting Naive Realism"
I don't agree with Searle's solution to the epistemological problem of how we can gain knowledge of objects in the real world from private sense data, how we can know the public objective from the private subjective and how we avoid scepticism, subjectivism and solipsism.
Searle proposes the "intentionality of perception". Whereas I agree that we are shaped by evolution, and the object causes the visual experience, I don't agree that the intentional content of our minds (intentional state) is causally self-referential. IE, I may perceive a car, but it is the car that has caused me to have that very perception. Such self-referential causality is inadequate to ensure a condition of satisfaction between the intentional content and object in the world, whether a veridical perception or an hallucination.
Searle tries to avoid Kant's transcendental link between intentional content and actual world by attempting to naturalize intentionality, ie, treating intentionality as just another biological function using a self-referential intentional causation.
Searle attempts to show that a self-referential causation between intentional content and world will ensure that any link between intentional content and world will be logical rather than empirical, and therefore directly observable, avoiding Hume's problem of inference using regularity of observation.
Searle's approach fails because he ignores the asymmetry of cause and effect, and incorrectly assumes a symmetry in the direction of fit from world to mind and from mind to world.
Such asymmetry between cause and effect and effect and cause means that the link between intentional content and actual world cannot be self-referential, as is required by Searle in his support for naive realism. -
Is indirect realism self undermining?Who said that there's such a thing as "direct realism"? — Alexander Hine
From Wikipedia Direct and indirect realism
"In contemporary philosophy, indirect realism has been defended by Edmund Husserl[17] and Bertrand Russell.[9] Direct realism has been defended by Hilary Putnam,[18] John McDowell,[19][20] Galen Strawson,[21] and John R. Searle.[22]"
From John R. Searle The Philosophy of Perception and the Bad Argument
"I realize that the great geniuses of our tradition were vastly better philosophers than any of us alive and that they created the framework within which we work. But it seems to me they made horrendous mistakes."
"The second mistake almost as bad is the view that we do not directly perceive objects and states of affairs in the world." -
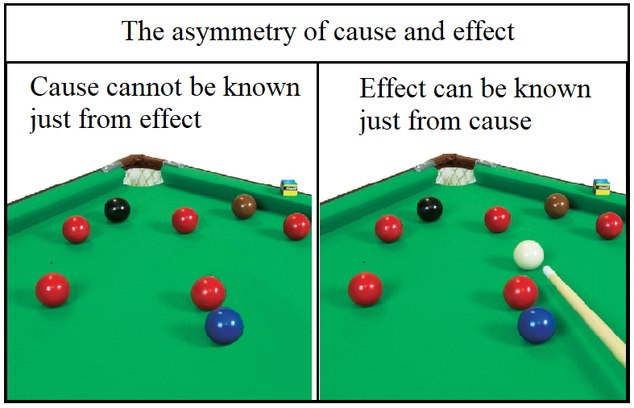
Is indirect realism self undermining?I may be absolutely certain of what I am seeing, whether a tree or snooker balls on a snooker table, but knowing the present effect doesn't allow me to know the preceding cause.
As I cannot know from the position of the snooker balls in the image the preceding state of affairs, I cannot know from seeing an image of a tree the preceding cause of that image.
A Direct Realist would need to explain how the cause of an effect may be unambiguously known just from knowing the effect.

-
Is indirect realism self undermining?The onus is on direct realists to explain, if only broadly and superficially, how direct realism is supposed to work. Thoughts? — frank
Pierre Le Morvan wrote an article Arguments against Direct Realism and how to counter them
A major problem with Direct Realism is the belief that because one knows an effect, such as the image of a tree, the cause of that effect can be directly and unambiguously known. -
Is indirect realism self undermining?The guy on the left is an image of direct realism. He doesn't get a cloud. He just directly sees the tree — frank
You say the Direct Realist is not seeing an image of the tree, which is what the Indirect Realist would say, but is directly seeing the tree.
An Indirect Realist would say that they are looking at an image of the tree, and therefore don't know, just from the image, whether the tree is 5m tall 10m away or is 10m tall 20m away.
If the Direct Realist is directly seeing the tree and not an image of the tree, how does the Direct Realist know, just from the image, whether they are looking at a 5m tall tree 10m away or a 10m tall tree 20m away ?
How can the Direct Realist justify that they are not looking an an image of the tree ?

-
Refute that, non-materialists!@Eugen In Physicalism, everything is physical. But the question remains, is a protoconsciousness an intrinsic part of the physical.
-
Refute that, non-materialists!What's the difference between protoconsciousness and matter? — Eugen
I would use the term Physicalism rather than Materialism. Physicalism is closely related to Materialism, but Physicalism grew out of Materialism with advances in knowledge about the physical sciences. In the world of space-time there is more than just elementary particles but also elementary forces.
Therefore, an understanding of consciousness needs more than an understanding of matter but also the forces between this matter. The question with the mind-body problem is how consciousness is grounded in broadly physical systems, how the property of feeling pain could be instantiated by an entirely physical object, such as the nervous system.
Referring to the SEP article Russellian Monism, according to Bertrand Russell, fundamental physical entities are intrinsically qualitatively special such that they necessitate conscious states in macro structures, such as humans, but as yet, our understanding outstrips current knowledge. Russellian monism comes in two varieties: panpsychist and panprotopsychist. The former holds that the special intrinsic properties are themselves consciousness properties, and the latter denies this.
I find it hard to believe in panpsychism, in that electrons are conscious, but panprotopsychism seems a more sensible approach, whereby elementary particles and forces have certain intrinsic properties that enable the realization of consciousness in certain circumstances. For example, the property of movement cannot be observed in a system consisting of a single magnet, yet can be observed in a system consisting of several magnets in close proximity. It is also the case the the property of momentum of an objects exists neither in its mass or velocity, but is a product of the two. The property of volume of an object doesn't exist in its parts but in the relation of the parts making up the whole. Perhaps in the same way, the property of consciousness cannot be discovered in an individual element, but only emerges when several individual elements are combined in certain particular ways.
Perhaps protoconsciousness is an intrinsic feature of elementary particles and forces that only emerges as the property of consciousness when these elementary particles and forces are in certain combinations. -
Refute that, non-materialists!Ok... elaborate a bit please, it looks like you're saying something there — Eugen
Intellectually, my belief is that of Neutral Monism, where reality consists of elementary particles and elementary forces in space-time. Consciousness may be explained by Panprotopsychism. However, the unity of consciousness, the neural binding problem, Kant's unity of apperception remains beyond comprehension, and must remain what McGinn called Mysterianism.
On the one hand I cannot believe in Conceptualism but on the other hand I know Conceptualism is true.
As an "experience" is a concept, and therefore a type, perhaps the wording should be "there are no experiences, only tokens of experiences", though I know what you meant, which is the main thing. -
Refute that, non-materialists!But, if I were a materialist, I would go further and eliminate the notion of Type altogether. — Eugen
If I started as a Materialist, this would lead me into becoming a Physicalist, and eventually a Panprotopsychist.
I would have thought that to be a Materialist means rejecting the notion of a type. A Conceptualist would accept the existence of types in the mind, but I don't think that a Materialist would be a Conceptualist.
There are no types of experiences, only experiences. — Eugen
As an aside, an "experience" as a concept is a type. -
What is computation? Does computation = causationI referenced cognition because the most popular models of how the brain works are computational — Count Timothy von Icarus
Numbers are computed in language
If asked the question "what is one plus one", as the answer is not contained in either number, I need to carry out a computation in my mind.
If I put one pebble on a table, and then put another pebble next to it, I can see two pebbles.
I don't need any mental computation to know that I see two pebbles, in the same way that I don't need to compute that I see the colour green. Seeing the colour green is the direct effect of the cause of a wavelength of 550nm entering the eye.
Regarding causation, if Bertrand Russell was correct that the notion of causality is objectively redundant, there would be no work for the National Transportation Safety Board which investigates every civil aviation accident in the United States, for example.
Therefore, I only need to carry out a computation if presented with a problem expressed in language, ie, in the computation of numbers where language and naming cannot be ignored. In language, one object is named "one". When another object is added, the set of objects is named "two". When another object is added, the set of objects is named "three", etc. Therefore, when I see one pebble on the table, I can say "I see one pebble". When I see another pebble added I can say "I see two pebbles". I can then answer the question "what is one plus one" as "two".
Therefore, the computation of numbers within the mind can only occur within language. -
What is computation? Does computation = causationIn terms of grouping rocks together, it's probably easier to conceptualize how the cognition of "there are two rocks over there," and "there are 12 rocks over there," requires some sort of computational process to produce the thought "there are 14 rocks in total." — Count Timothy von Icarus
If I see two rocks on the left, I know that two objects has the name "two".
If I see twelve rocks on the right, I know that twelve objects has the name "twelve".
If I see fourteen rocks in total, I know that fourteen objects has the name "fourteen".
IE, I know there are fourteen rocks in total not from any computational process but from how objects are named. -
What is computation? Does computation = causationWhat is computation? — Count Timothy von Icarus
As a non-mathematician, I am curious about the following:
Question one: if I put one pebble on a table and alongside it put another pebble, has a computation been carried out ? Because, whatever has happened has proceeded in a series of steps, within the system there has been a change in information, something has caused the pebbles to move, time and energy have been needed, two has been instantiated in the physical world as two pebbles but also two exists as the abstract object two and two pebbles existing as a single whole is different to two pebbles existing as two separate parts.
Question two: if in the absence of any observer, a pebble moves alongside another pebble
under natural forces, has a computation happened ? -
Who Perceives What?If the mind, the brain, or the little man can perceive sense-data, representation, idea, both the perceiver and the perceived ought to be able to stand in direct relation to one another, where one perceives and the other is perceived. — NOS4A2
If the mind is the perceiver and the idea is the perceived, and the perceiver and perceived are separate entities, how can the mind ever have knowledge of the idea if the idea is forever separate from the mind?
The point is, perceivers have most if not all of the above. Therefor perceivers are not brains, minds, or homunculi. — NOS4A2
If the perceiver cannot be found in either the mind or the brain, where exactly is the perceiver? -
Who Perceives What?The mind-mediated reality is also determined in pre-cognitive ways by a mind-independent actuality that cannot be real for us, even though we cannot but think of it as being real in itself. — Janus
Are you referring to Innatism, Enactivism, Kant's a priori intuition, etc, in that life has evolved in synergy with the world for at least 3.5 billion years. I agree, if you are. -
Who Perceives What?This is incorrect. Wittgenstein is saying that this picture of naming something private drops out as inconsequential in terms of how we understand what is being communicated. — Richard B
According to Wittgenstein, in addition to the fact that no one can ever never know the private perception of another, but can only infer it from their behaviour, the object can play no part in the language game. The name "pain" may have a use in a language game, but not as a name for a particular thing existing in the world.
This is incorrect. See above. Both are perceiving, talking about a publicly shared object. Not providing proof of what they are supposedly perceiving privately. — Richard B
From Wikipedia - Naive Realism: Things in the world are perceived immediately or directly rather than inferred on the basis of perceptual evidence. According to the naïve realist, the objects of perception are not representations of external objects, but are in fact those external objects themselves.
An Indirect Realist would need proof, but a Direct Realist wouldn't, otherwise they wouldn't be a Direct Realist. To be a Direct Realist is to subscribe to the idea that their private perception is directly of the public object.
But they cannot distinguish between the two “sense datum” of the picture, they are the same. The positing of “sense datum” does not explain why they report a rabbit one time and a duck another. So, “sense datum” has no explanatory power in this case. — Richard B
Someone may first see a duck and later see a rabbit, but they cannot see a duck and a rabbit at the same time. At one moment in time there can only be one intentional object. -
Who Perceives What?I draw a stick figure of a person from my imagination. I show this picture to a child and ask her "what to you see?" The child may reply, "I perceive a stick figure of a person." Can we not claim that the child directly perceives a picture of a stick figure? — Richard B
Wittgenstein's Beetle in the Box argument can be used against Direct Realism
Wittgenstein uses the beetle in a box to argue that a language understandable by only a single individual is incoherent, ie, his private language argument. Para 293 of PI: "Suppose everyone had a box with something in it: we call it a "beetle". No one can look into anyone else's box, and everyone says he knows what a beetle is only by looking at his beetle." He argues that no one can ever never know the private perception of another, but can only infer it from their behaviour.
If Direct Realism was correct, given a picture of a stick figure in the external world, I would directly perceive the stick figure, and the child would directly perceive the stick figure. This would mean that I would know that my private perception was the same as the child's private perception, and vice versa. But this would contradict Wittgenstein's private language argument.
The famous picture of the "duck-rabbit" is an illusion. If presented to someone, they could see the picture as a rabbit, or, another time, see the picture as a duck. However, could we not say the what we perceive is the same figure in both cases? If so, the positing of sense data has no explanatory power in this case to explain this illusion. — Richard B
The Argument from Illusion can be used against Direct Realism
Searle refers to a similar argument used by the Indirect Realists to argue for the existence of sense data. If you hold up one finger and look into the distance past the finger, you will not see one object but will see two sense datum. This means that it is not the object you are directly looking at but the sense datum. Then, when you look at your finger, it may appear that you are directly looking at an object, but in fact you are are directly looking at sense datum.
When someone looks at a duck-rabbit they can only see either a duck or a rabbit, they cannot see both a duck and rabbit at the same time.
Imagine they see a duck. As before, they look into the distance past the picture and will see not one object but two sense datum. This means that it is not the object they are directly looking at but the sense datum. Then, when they look at the picture, it may appear that they are directly looking at an object, but in fact they are directly looking at sense datum. -
Who Perceives What?And this is suppose to turn me into indirect realist because of the causal train of events. — Richard B
Pierre Le Morvan in his article Arguments against Direct Realism and how to counter them is making the valid point that a Direct Realist can accept causal indirectness without accepting cognitive indirectness.
But I do not think the direct realist should be concerned about how we perceive, but how we learn and use the word “perceive”, how we make judgements about what we perceive, or how we gain knowledge from what we perceive. — Richard B
Surely a Direct Realist doesn't need to make any judgement when perceiving the colour green, for example, as they directly perceive the colour green. It is the Indirect Realist who needs to make a judgement when perceiving the colour green. -
Who Perceives What?For the indirect realist, though, something within the man (the mind, the brain, a little man) directly perceives something else within the man (sense data, representation, idea). But the boundaries between both X and Y are so unclear and amorphous that it could rather be the case that X is directly perceiving X. — NOS4A2
I also said “the boundaries between both X and Y are so unclear and amorphous that it could rather be the case that X is directly perceiving X.” — NOS4A2
The perceiver and what is directly perceived by the perceiver must be one and the same
There is X, the mind, the brain, the little man and there is Y, sense data, representation, idea. X is the perceiver and Y is what is perceived.
As Searle said, pain cannot be removed from the experience of pain. Similarly, what is directly perceived cannot be removed from the perceiver.
As Brentano said about intentionality, mental states are an incomplete essence, in that they cannot exist unless they are completed by something other than themselves. The relation between the intentionality of the mind and the intentional object cannot be a causal relation.
For the mind to understand an object it is perceiving, the mind must have ideas about the object. The ability to have ideas must be part of the essence of the mind. The mind, distinguished by the ability to have ideas, is then able to perceive ideas.
But if the mind is X, and Y is ideas, and if the mind is distinguished by its ability to have ideas, then X must by Y.
How can we perceive a concept that exists only in mind if our eyes point outward, not inward? — NOS4A2
The whole concept may only exist in the mind but the parts on which the concepts are based exist in the external world
When we look at a green tree with three branches, we are looking at one particular instantiation of the concept "tree". When we are looking at a particular set of colours and shapes, we perceive it as being one instantiation of the concept "tree". The concept "tree" does not exist in the world, only in the mind. The instantiation of the concept exists in the world. So we are perceiving two things at the same time, the instantiation of the concept "tree" existing in the external world and the concept "tree" existing in the mind.
But the instantiation of the "tree" that we perceive is made up of parts, consisting of a set of colours and shapes. For example, the colour green, a vertical line, three and a horizontal line.
Searle when discussing the science argument against Direct Realism comments that colours such as red don't exist in the world but only in our own mind. The colour green we perceive doesn't exist in the external world but only in our mind.
When looking at a vertical line, we are again perceiving two things at the same time, a particular instantiation of the concept "vertical line" as a set of points existing in the world and the concept "vertical line" existing in the mind.
Similarly when looking at a horizontal line.
As regards the number three, I would argue that numbers only exist as concepts in the mind, though others would disagree. Though if colours and shapes are concepts, then why not numbers also.
The end result is that when we perceive a green tree with three branches, we are in fact perceiving two things at the same time, a set of points existing in the external world which we determine as a green tree with three branches using concepts existing in the mind.
As Searle writes about intentionality and causality, in belief, validity is achieved when the mind matches the world, and in a valid desire the world must come to match the world. The conditions of satisfaction for an intentional state is self-referential, in that perception has a part of its very meaning that it be a state caused by the object represented in it. Searle would say that I have a visual experience with mind to world fit whose intentional content is that there is a green tree with three branches before me and that there is a green tree before me causing this visual experience.
When the Direct Realist says that they are directly looking at a green tree with three branches in the external world, what this means is that they are perceiving on the one hand a set of point in the external world and on the other hand perceiving concepts existing in the mind.
As Searle asks, how do we avoid scepticism, subjectivism or solipsism if our understanding is through concepts which only exist in the mind. Our knowledge of the world derives from the causal connection between points in the external world existing in time and space and our experience of them, and making sense of these experiences using concepts that exist in the mind perceiving these experiences. -
Who Perceives What?Even if it was true that trees are concepts that exist only in the mind — NOS4A2
You wrote: "For the direct realist, the man directly perceives a tree............For the indirect realist, though, something within the man (the mind, the brain, a little man) directly perceives something else within the man (sense data, representation, idea).
If the man directly perceives a tree, and the tree is a concept that exists only in the mind, doesn't this mean that the man is an Indirect Realist ?
I would agree with that.
RussellA

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum










