-
Thoughts on EpistemologyIf I flip a coin and cover the result before we see it, it must be either heads or tails, even before I lift my hand. — Banno
So have you sidetracked sufficiently from the original issue which was about the truth or falsity of events either yet to happen or yet to fail to happen? -
Thoughts on EpistemologyThat's a bit convolute. Again, this does not apply only to statements about the future; there are plenty of other sorts of statements which are true and yet unknown. It's more just pointing out the difference between belief and truth. — Banno
Shy away from the conclusion, but that’s what you are faced with.
Your statement concerns a possibility of which there is as yet no fact of the matter. The PNC fails.
So the statement is a timeless assertion. And yes it is framed in terms of the laws of thought. But it relies on the inductive evidence - some temporal act of measurement - to determine whether it is justifiably believed as either true or false.
As usual, you want to revert to naive realism. Truth doesn’t require a locus of enquiry - the interpretant for whom the answer serves a meaningful reply. It doesn’t require some actual act of measurement as inductive evidence. You want the “true facts” to transcend the whole business of reasoned inquiry.
So you caught yourself out in using a concrete case - claims about the future where it is an impossibility for the necessary act of measurement to have been made. You are trying to backtrack with speed and talk more vaguely about all the truths that must be simply unknown facts - safely either current or in the past.
But you already exposed the basic flaw in your position. No getting out of it I’m afraid. -
Thoughts on EpistemologyThat we do not know the truth of some statement does not render it neither true nor false. That's the case for a wide range of statements, including statements about the future. — Banno
Mmm, yeah. You mean that statements are essentially timeless, while the world itself has temporal structure.
That is what your critics have been telling you for some time, Banno.
I rather like the block universe — Banno
People like to believe all kinds of weird stuff. So your preferences are irrelevant. -
Thoughts on EpistemologyIf both are still possibilities, then neither is yet an actuality.
Of course in a block SR, modally realistic, quantum multiverse, the timeless realm of propositions becomes one with a timeless world. Time falls out of your metaphysics. The frozeness of a statement matches a frozen view of reality.
But still, that feels a little extravagant as your metaphysics, no? Do you really want to have that as your position? -
Thoughts on EpistemologyBut either way, that we don't know if some statement about the future is true or false does not make it neither true nor false. — Banno
Correct. It makes it vague. The PNC fails to apply. At this particular point in time and space.
Again, you are simply trying to talk around the difficulty that others can so plainly see with your position.
To talk timelessly of the world and it states does not make the world itself a timeless place. -
Thoughts on EpistemologyMeh. Not unless we need to. — Banno
If you accept the metaphysical extravagance of an SR block universe, then you have no grounds for rejecting those further metaphysical extravagances.
So you have to show what could place a realistic constraint on the models you choose to treat realistically.
Oh, the irony. -
Thoughts on EpistemologySo let's go with a block universe. — Banno
Next stop, the quantum multiverse and modal realism. -
Thoughts on EpistemologyThe dualist solution to this apparent regress is very simple. — Metaphysician Undercover
Yeah. Bring on the soul-stuff. That'll work. -
Thoughts on EpistemologyThe information recorded in a memory is not a temporal event? — Janus
It was an event when it happened. But even then, there was the displacement - the transduction step - which was its recording. The physical event became an informational event - a sign of the thing. And yes of course, that requires a whole physics of information recording.
Minds need a body to be embodied models. Let's not pretend it is confusing. The whole point of semiotics or the epistemic cut is that signs are physical acts - acts of measurement. But, Janus-like, symbols have two faces. They are both physical marks (essentially meaningless, like a scratch on a rock) and they are informational (essentially meaningful to a system of interpretance).
I can get the notion of temporal displacement, how it enables freedom from the constraints of particular times, but I can't see how that translates into timelessness or eternity. — Janus
Maybe that is just the reification. There might be a difference - a big one - between timeless and eternal for all practical purposes, and timeless and eternal in some dualistically absolute and non-pragmatic sense.
Again, this is where physics itself has got to. The Comos is organised by its own informational limits - the famous holographic principle that accounts for blackhole entropy and the possibility of an actually future-eternal heat death geometry for the Universe. -
Thoughts on EpistemologyI recall reading in Russell the assertion that once something has happened it remains forever true that it has happened, and even that it is true now and forever that whatever will happen in the future will happen in the future. — Janus
The past may be certain, but the future is full of possibilities.
So if Russell said this, he was surely just giving voice to the widespread confusion over how deterministic physics is in fact .... the map and not the territory.
Our models of physics generally have the property of being time reversible. The equations encode a symmetrical relation with no preferred direction. They have to so as to fit a cause/effect model of reality. The past state that maps to the future state must commute. That future state must map back to the past for the simplistic maths to work and preserve the efficient causal relation being claimed.
So this is what mechanics is about. Reducing reality to models of causal entailment. Mapping a prior state onto a future state in a timeless fashion. Going forwards in time has to look the same as if we were instead travelling back.
It's not a problem as we know how to break the symmetry of these symmetric equations. We know that the variable we plug into them are the initial conditions. They are the information that comes from the past.
But to the degree the world is mechanical and deterministic, we can also do the reverse. We can start with the final state and work back to predict what must have - retrocausally - been the initial conditions.
Of course, we also know that such physical situations are rare rather than generic. After all, there is an even more fundamental law in the laws of thermodynamics where time now has a preferred direction due to entropification. Every actual physical process is frictional or heat wasting. That is information lost irrecoverably to an environment (Maxwell's demon argument).
So you can't actually measure the full final state needed to run your deterministic equations in reverse. The critical details are almost sure to have escaped. And the more complex the system - the more realistic it actually is - the faster the information gets dispersed as statistical entropy.
All this seems logical enough; but the troubling question is as to what such timeless truths really consist in beyond our thinking of them. If they consist in nothing beyond our thinking of them then they are not really timeless at all, because our thinking is a temporal event. If they consist in something beyond our thinking of them, then what could that be but some eternal logical 'substance', universal mind, or God? — Janus
It's not the truths that are timeless. It is the information recorded in a memory.
So a model exists "outside" of the time of the physical process it models. It is displaced. There is an epistemic cut.
And a model is only "the truth" in a semiotic sense. It is a model of the world with us in it. So it is the world as it is the most convenient and purpose-serving for us to imagine it.
The model thus constructs "the interpreter" along with "the interpreted". The self becomes this timeless set of "truths" - or semiotic habits - that stands apart from the world it is in the habit of regulating according to its desires.
The "truths" captured by this interpretive relation are not really truths at all. They are not the mind-independent facts of the world. But nor are they just idealist mental constructs. They are what is "true" about some self-interested system of interpretance - like an organism with an interest in autonomy.
So an interpretive relation is true to itself! It is capturing the facts of how to be in a pragmatic or functional relation with the world ... as an organism.
Now if you then extend semiosis to the Cosmos or Existence in general - make the leap to pan-semiosis - then you would be getting at the truly timeless and mathematical-strength habits of nature. You would be treating reality as a mind-full organism, or at least a purpose-driven dissipative structure.
However I always agree that pan-semiosis is speculative metaphysics. Science hasn't quite got there, even if it is knocking on the door with its information theoretic turn, its new ontic structuralism. -
Thoughts on EpistemologyIn order to use a map one must understand the little crosses and lines as being buildings and roads and stuff. — Banno
Banno gets this, but refuses to address the issue of what is a principle. — Metaphysician Undercover
I'm not sure many maps are crosses and lines. Was Banno thinking of pirate maps? Normally those also have a palm tree and an instruction of how many paces to the west. :)
But seriously, to get the point of Korzybski, he was saying that the map you find so useful as a model of the world is not the world. In fact, it functions by abstracting away as much of the physics of the real world as it possibly can.
So the argument is against representationalism - the idea that the mind puts reality on display in some direct naive realist fashion.
This is the essential problem with Banno's thinking. He wants to have a direct and veridical relation with the world. He wants nothing to intervene between his beliefs and the real facts. He is a good old fashioned Cartesian, but wants to deal with that by refusing to acknowledge his dualism of self and world. He pretends that because the relation feels direct and unmediated, that warrants an epistemology that just takes the relation to be direct and unmediated.
However Korzybski got the fact that the modelling relation is not about veridical representation. The interpreter doesn't want to have to think about the whole of reality. S/he just wants simple signs telling him/her exactly how to react on any given occasion. The interpreter wants to function as a set of habits triggered by repeatable acts of measurement. The world - as represented in the interpreter's world model - should be reduced to a simple set of stop/go signs.
This is anti-representational. The signs that constitute the map - or state of perceptual awareness - should be whatever can serve to get rid of the most unnecessary detail possible.
It flips our usual intuitions on their head. But psychological science is perfectly familiar with the story. How else could the complex energy of the world get turned into some neural traffic of digitised spikes?
So yes, a map might be just the barest thing of lines and crosses. Or a few named landmarks and named roads.
In recursive fashion, this is even simpler than the world as we model it neurobiologically. Our eyes see buildings, roads and stuff. That is the level of modelling at which we navigate using the biology of perception. And it is impressively direct and veridical - if you don't know the first thing about the actual psychophysics of our neural-level models.
But then, at a cultural and linguistic level, we can construct paper maps that abstract the essentials of our experiential maps. We can operate as interpreters seeking useful habits at this secondary level of semiosis. We can transcend our animal state by becoming creatures of even greater symbolic abstraction.
The map and the territory story was meant to draw attention to this - the way that cognition is anti-representational. Modelling works by reducing a complex reality to the sparsest acts of measurements that can reliably do the job of getting us about the world.
And yet Banno can't help himself. He has to jump to the representational veracity that he believes warrants his naive realism. Look everyone, there is the buried treasure, right where the map said it was! -
Thoughts on EpistemologyTake the map/territory example. These two are both objects, so there is no epistemic cut between these two. — Metaphysician Undercover
Yeah. I've said many times now that a dualistic ontology can't cut it. It has to be a triadic relation. So someone has to interpret the map to navigate the territory.
Thus the further thing of the interpreter must either be addressed by the metaphysics, or else it sets up the familiar homuncular regress.
A further obvious problem with a map is that it is representational. It is passive. It can't physically do anything to constrain the physics of the world.
Well it does if you are reading it and saving your legs by not getting lost. But the epistemic cut is about the need for some actual hinge point, or transduction step, where information and physics truly make contact.
Hence we have Pattee's focus on how a molecule can function as a message - how DNA can code for a protein that is then an enzymatic signal to switch on or off a metabolic process.
So Peirce gives us the general triadic need to include the notion of interpretance in any modelling relation with the world. And Pattee focuses on the practicality of the machinery that connects the interpretance and the world.
The usual dualistic bind that plagues representationalism is resolved by this modelling relation where the informational aspect of nature is tied in an interactive feedback loop with the material aspect of nature. -
Thoughts on EpistemologyTo model the world, we must turn it into a set of measurements. A set of measurements is not the world. It is as simple as that.
-
Thoughts on EpistemologyLike Banno, whatever makes you happy I guess. I couldn’t even begin to untangle the misconceptions in all that.
-
Follow up to Beautiful ThingsThe creative process consists of taking matter and forming it. — Cavacava
I don't think so. It is primarily about making ideas manifest. Matter doesn't actually need to be involved.
What matter does poetry depend on?
I don't agree that this is only about social purpose to art, which is important in that it negatively drives artists to explore the unusual, the new. — Cavacava
How is that not a social purpose? Whenever has a great artist not been judged as such within a social context?
He thought that what is beautiful is pleasurable, but what I think what the art world is finding is that reality can rendered beautiful, regardless of whether or not it is pleasurable, that the aesthetic effect can also be painful. — Cavacava
So modern art has discovered the pleasures of masochism? :)
As I say, neurobiologically we can see the connection between our reward system and the discovery of a satisfying match.
Our brain goes aha! It secretes a little squirt of dopamine. It says the connections we have just made are valuable and worth remembering, worth turning into a habit.
As I said, my response was targeted at an objective reason for such an "aesthetic" response. What are we recognising when we recognise beauty in the world?
When it comes to masochism, what is being recognised there? Is it the deserved rightness of the humiliation? Does that fit the masochist's rather particular model of the world?
Whatever, a challenging work of art is not really aiming to be a beautiful work of art in the terms of being a beautiful material form of some kind - a physical image, or shape, or sound. It is aiming at being - challenging. And that too can elicit neurobiological reward, especially when the challenge is mastered and used as evidence of our being part of some valued social clique. It is a sign we have joined the club.
But also, as I argued, challenge just is rewarding in its own right. The brain is evolved to master challenge in a general fashion. And feel good when it does.
It's complicated, but not impossible to understand. -
Thoughts on EpistemologyAnd you are such a rude bugger. — Banno
Rather than trolling, just deal with the arguments for a change.
Hint. Telling me "you have a feeling" is not an argument. It is a confession you just lost the argument. -
Follow up to Beautiful ThingsThese are properties of form, not matter. — Cavacava
So there is matter without form?
And do we go to galleries to look at the wonderful pigments, go to concerts to hear the splendid notes? That sounds wrong, doesn't it.
I agree that surprise has a lot to do with it, but we still have a very Platonic/Greek, the classical conception of beauty. — Cavacava
Yeah. There was a reason why the celebration of the ideal was a Greek thing. It was a huge surprise.
It was only with the Romantic movement that "wild nature" - the thunderous sky, the treacherous sea, the dangerous mountains - became celebrated for its fractal vigour.
So what part of nature a culture celebrates does change as it becomes accustomed to its past surprises.
The surprising works of Du Champ, Kandinsky, Picasso, Pollock and others have begun to change that conception. The problem with the classical conception of beauty (I think) lies is its connection to a conception of the divine which became prevalent during the Renaissance and has remained so. — Cavacava
I agree. Art became about the human individual. It started as mythic, then it became symbolic of social hierarchy - the church, the Medici, the upper class - and finally it becomes the celebration of essential humanity. The most modern of our mythologies.
But this is to talk about the social purpose of art. The question was about there being some objective basis to our aesthetic reactions. Why is DuChamp's urinal beautiful? Is that because of its social commentary or because it expresses some deep mathematical form of nature?
I don't think that one is an example of the latter.
So I'm not saying the issue is not more complex.
Look at Lucian Freud's works. Many of his works are hyper-realistic. It was not unusual for him to spend 1500 hours on a portrait. They are not beautiful in any classical sense, but they are beautiful. He managed to use hyper-realism to transcend what is simply realistic. The beauty and the truth of his work startles you, its aesthetic affect as it transcends our normal sense of what is real.
Or look a Pollock's splatter paintings...matter is here overtly presented with the artist allowing form to arise from the juncture of the pigments on the surface of the canvas, and not by any thought of fractals or symmetry. Kandinsky takes subjective feelings and presents them corporeally. Even Picasso's who changed styles multiple times, can hardly be said to have followed a classical notion of beauty for many of his works.
I think similar notions hold true in music, such as the a-tonality of Schoenberg, the sounds & lack of sounds of John Cage and others. — Cavacava
Again, I was talking about the objective basis of an aesthetic response. There are reasons why brains would be sensitised to symmetry, economy of effort and balance. It feels rewarding to spot that as it is a useful thing to be able to see.
Now you could argue that Pollock is an example of fractal complexity and dynamism. If it has an actual visual appeal, that is it. What else could there be?
But the aesthetic response is really something else - that delightful feeling of social transgression which affirms the essential genius of the individual. So as I say, it is social iconography. The aesthetics of cultural snobbery if we are honest. We can feel the pleasure of being part of the club that gets the attitude.
So there is an aesthetic response - a buzz of dopamine in some secret compartment of the brain. :)
But that now reflects the extent to which we have evolved to be social creatures. We are evolved to seek intelligibility in a social world as well as a physical one.
So the same system of rewards for decoding the natural structure of our worlds. But not now aimed at the simple mathematical forms that underly the material world. Instead, aimed at the subtle geography of our social hierarchies, and our supposed place within them. -
Thoughts on EpistemologyIn another sense, "the map is not the territory" is quite problematic. — Banno
Of course. Hence why you are already wandering off down a familiar and reassuring seeming path - semiotics as Sausserean dualism. Displacement as what Derrida meant.
You are going to find semiotics "problematic" while you continue to attempt to assimilate it to good old Kantian representationalism.
If you don't get the irreducibly triadic structure of a sign relation, you haven't yet got it at all.
As I said, our model of the world is really the model of us in that world. The displacement is not dyadic but another rung up from that. The world becomes the place we also discover ourselves. And you need an epistemology that has that structural recursion.
Again, google some real writers on the issue - Pattee's epistemic cut, Rosen's modelling relation, Von Neumann's self-reproducing automata. -
Thoughts on EpistemologySo displacement is where one talks about something in a different place to where it is happening? — Banno
Nope. ;) -
Thoughts on EpistemologyWell it is the central thing to a semiotic metaphysics. So yeah.
A modelling relation with the world is based on the displacement that is the separation of the model from the world it seeks to regulate.
The idea is terribly simple and familiar. The map is not the territory, etc. I get tired of all the pretence that this is something esoteric and not merely a precision description of the ontology involved.
If you want a more technical framing, Pattee's slogan is that life is based on the dichotomy of rate independent information and rate dependent dynamics.
But let's cut out all the feigned shock and horror. The epistemic cut is perfectly straight-forward. -
Thoughts on EpistemologyYou appear to have introduced a technical term - displacement - without telling us how you are using it. — Banno
Err. Pattee's epistemic cut. Rosen's MR systems. Von Neumann's self-reproducing automata. :)
If you want the technicalities, look them up. -
Thoughts on EpistemologyI'm sure you were making this point. It started back here - https://thephilosophyforum.com/discussion/comment/145216
But yes, I see Cavacava is too. That's encouraging. -
Thoughts on EpistemologyI don't understand this sentence. Can you clarify? — Banno
It is not a flaw but the reason why it works. -
Thoughts on EpistemologySO add a time and place, if you like — Banno
Yes. You can keep adding displacement. As much as you want. But that doesn't absolve you of the need to account for that machinery of displacement. Your anti-Cartesianism still misses the point. -
Thoughts on EpistemologySaying that the cat is on the chair and saying that "the cat is on the chair" is true amount to much the same thing. — Banno
Except that one is a spatiotemporal occurrence and the other is a timeless assertion. Janus tried to point that out.
There is a gap - or epistemic cut - that epistemology still needs to account for. The fact of a displacement in terms of our ontic commitments is the epistemic feature and not the metaphysical bug.
So trying to collapse that - as in attacking the Kantian dualism of scheme and content - is philosophically obtuse. -
Thoughts on EpistemologyAs Wittgenstein responded to his own question of whether he was really just a "behaviourist in disguise" and whether, for him, "everything except human behaviour is a fiction", he said, "If I do speak of a fiction, then it is of a grammatical fiction." — Luke
Again, the complaint I have here is that it fails to distinguish grades of semiosis or "grammatical" structure.
So yes, you can look to behaviour as speaking to what is truly believed. That is the turn from Kantian cognitivism to a Pragmatic enactivism or embodied cognition - a Peircean sign relation with the world. We betray our beliefs in our actions.
However the human mind has a double structure. It is structured both at a basic animal/neural level, and then that is elaborated on by a social/linguistic level of semiosis. So there is a neural code and speech code in play.
Semiosis is then about how codes in general are about constructing useful "fictions". Both our neurology and our sociology want to reduce reality - the noumenal - to the phenomenal, an umwelt. We want a reality that is a play of interpreted signs. We want a view of the world that is not of the world in itself, but a view of our selves in a world that has an intelligible structure.
So there is a general semiotic logic at work which founds any notion of what counts as truth. And the component that is generally neglected is indeed - where Wittgenstein is correct - that the truth is the truth that is this view of a world within which we exist.
The rub is that this "we" is a construct. And not just a social/verbal construct, but also a biological/neural construct. And so there is a double "grammatical fiction", a layered "grammatical fiction", at the centre of any theory of truth debate.
That is what I have consistently argued. But most folk seem attracted to Wittgenstein because he seems to promise an end to exactly that kind of complex analysis.
Peirce is "too difficult", "too tricksy". Give us quietism and an end to metaphysics. Let us just slay Descartes and Kant and not worry about what more sophisticated epistemology has to replace them. Let us just return to our dogmatic slumbers and dreams of naive realism. -
Follow up to Beautiful ThingsWell, I think the answer is "sort of." Probably no particular thing is universally beautiful. The things I consider beautiful are personal. — T Clark
You can see something physical at the heart of aesthetic judgements - natural properties like symmetry, balance, and economy of effort. So there are objective properties that appeal.
I would guess that is because our brains evolved to be pattern recognisers. We need to zero in on what is the most general condition of our world so as to appreciate what is then the particular or often, the wrong, the blemished, the marred, the imperfect.
I would add straight away that the brain also evolved to make good mate choices, to find good food, etc. So that would also play into our aesthetic responses.
But we can see a circle or square as beautiful in being highly symmetric. Or more naturally, our eye is drawn to geometries that speak to perfectly balanced growth and elaboration.
So why is the golden rectangle perhaps more appealing than the ultra-simplicity of a square. Is it because the eye can see the universal growth ratio inherent in it?
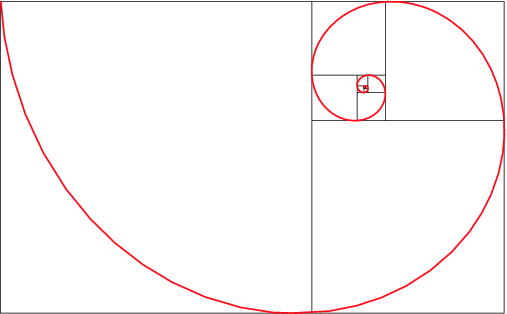
And why the appeal of mountains, surf, trees? Again what we likely appreciate is the perfect balance represented by fractal self-similiarity - a scale symmetry.
That's not the whole story of aesthetic judgements, but it seems the most objective part of our evolved responses. We have an eye for natural perfection as that then is what allows us to see its imperfections. The imperfect perceptually pops-out once we have a baseline ability to recognise the perfectly freely growing or elaborating complexity that defines a natural balance.
Then there is a more subjective slant on the same general neurocognitive imperative - to make the world easy to read at a glance.
We like compositions that are balanced in their familiarity and surprise. Again, it is about the Gestalt need to balance figure with ground, event with context, so that the world is felt to be intelligible and yet not dull. We want a work of art to reward us both in being deeply familiar and deeply unfamiliar. And the ratio might be that of the golden rectangle or logarithmic growth. So a spicy dash of surprise at every level while also a healthy base of confirmation of what we reasonably expect.
It is not hard to see how this applies in all aesthetic ventures from an oil painting, to music, to great cooking or a nicely furnished room. There is some ratio of the familiar to the surprising that meets the subjective preferences of a mind that wants to be able to safely predict its world and yet still be always learning, or steadily growing and expanding its range of experience itself.
So aesthetics could be explained ecologically by the needs of our brain to see through to the essential baseline structure of the world. The world is objectively what it is due to the nature of growth as a "mathematical" process itself. And then subjectively - to be good at building a model of the world - we need a psychological architecture that is also based on open-ended growth. That is how we can develop a good fit. We seek to find a good balance between habit and attention, between familiarity and surprise, in every moment.
So every aesthetic object or image should "test" our responses in that fashion. They should contain a brain-suitable balance of predictability and surprisal. There will be a ratio of the two that feels the most informational or meaningful.
Phi, or the golden ratio - 1.618... - could be the right number. Here is someone who suggests that: https://plus.maths.org/content/golden-ratio-and-aesthetics
There's a ton of psychological studies on preferences for complex stimuli, but I can't recall there being some magic number being identified. You tend to get general comments about a U curve, but not some special value.
The relationship between the complexity of a stimulus and its perceived beauty has been a topic of great interest with influential studies since the earlier experimental investigations of aesthetics. For instance, Berlyne showed that complexity is a dominant determinant of interestingness and pleasingness of a stimulus (Berlyne, 1963; Berlyne et al., 1968). Berlyne (1971) suggested that the relationship between complexity and pleasingness could be explained by an inverted U-curve, where the stimuli with intermediate levels of complexity are the most preferable ones. This concept of an optimal amount of stimulus complexity has been supported by numerous studies that found an inverted U-curve when characterizing aesthetic preference as a function of complexity (Vitz, 1966; Berlyne, 1971; Saklofske, 1975; Farley and Weinstock, 1980; Imamoglu, 2000).
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4796011/
This is probably because it is hard to get people exactly matched in their life experiences. We all might have a similar brain design, but also would all find somewhat different things surprising or familiar.
Plus the world itself is varied as an environment. All of nature might be fractal in its growth, but the slope of that line can be very different. A flat sea and a mountainous sea are both fractal, yet also at opposite ends of the spectrum in terms of beautiful monotony and spectacular excitement. -
Science is just a re-branding of logicWhen you go to the seaside, do your encounter a beach as well as the grains of sand?
Think about how you would naturally reply if a friend asked where you went at the weekend. -
Science is just a re-branding of logicWhat, the world isn’t structured by categorical relations? The notion of generals and particulars fails the test of naturalness? We are merely imagining that reality is organised hierarchically?
I find that hard to believe. -
Thoughts on EpistemologyInterpretation is moving from one language to another, yes? — Banno
Huh? That would be interpreting two different languages. And that could well involve the construction of a different sense of being a speaker to speak like a native.
How does interpretation work when we are both speaking English? — Banno
We would both share some point of view - enough of one so that the personal differences or personal quirks did not feel like they make an important difference. We would share the cultural identity involved. We would be the kinds of selves that entails.
And now can you address the questions I've asked of you repeatedly. It is boring dealing with these trivialities you post as replies. -
Thoughts on EpistemologyI've got no idea what an absolutely public language might be. — Banno
One where everyone shares the exact same interpretations with no personal nuance.
But even if you shout "fire", there's always going to be a few wondering what that could mean. -
Thoughts on EpistemologyDo as your professors advise then. Read the paper, put it into your own words, then I will grade you.
Or this search gives you 130 hits to explore.
https://thephilosophyforum.com/search?Search=epistemic+cut&expand=yes&child=&forums=&or=Relevance&mem=&tag=&date=All&Checkboxes%5B0%5D=titles&Checkboxes%5B1%5D=WithReplies&Checkboxes%5B2%5D=child&user=apokrisis&pg=p2 -
Thoughts on EpistemologyI use it like Pattee. I learnt if from him directly. But if I see you making an effort, of course I would help explain anything you might not understand or disagree with.
-
Thoughts on EpistemologyOnce more. Please answer the direct question.
The corollary was that public language is equally a matter of degree. Are you wanting to say there can be no absolutely public language? -
Thoughts on EpistemologyYou do not have to be here. — Banno
Still hoping to be in control of the discursive boundaries? Make this a safe space for that guy Banno? Remove the possibility of his authority being challenged?
But you enjoy this. — Banno
Of course. I love the immense variety of life. And without the irritation, it is easy to get lazy. -
Thoughts on EpistemologyAs I said, we would use the resources of the communal language, but would be free to create private words.
And what is more germane to my original argument - which was about the advantage of a pragmatic theory of truth - is that I am focused on the issue of the speaker doing the speaking. Who is this person really? Is s/he a social construct or is s/he a neurobiological individual?
There is both a division and a division that is not clearcut - relative and dichotomous rather than dualistic and absolute.
So I am focused on what it could even mean to be private - in any sense. Or public, in any sense. I am highlighting the fact that language - as semiosis or a triadic sign relation - has to make the I-ness that both speaks and appears to understand the speaking in right fashion. The production of actual language speaks to the successful production of the I-ness that we associate with "being a speaker expressing meanings".
Banno wants to talk about Davidson and that whole edifice of flanneling built on the possibility/impossibility of translation. This is somehow vitally important to put Cartesian dualism to the sword, not to mention Kantian representationalism.
Well good luck to all that AP still playing its philosophy of language long past its intellectual sell-by date.
Meanwhile over here - particularly at the intersection of science and metaphysics - Peircean semiotics is going strong. The essential issues have been framed in far more fruitful fashion.
Rather than trying to kill metaphysics, science is cashing it out as irreducibly complex triadic relations. Systems science, cybernetics, hierarchy theory, complex adaptive systems, and all the other ways of speaking about a holistic or organic understanding of existence.
So the issue is not "in what language", but "for what reason".
A systems perspective recognises the reality of final cause. And for there to be "a purpose" there has to be "a self" in some proper sense.
Hence the private does make no sense. That is the mistake of Cartesian dualism and Kantian representationalism.
But the public also makes no sense as that is a reification of the collective.
You need an actual theory of wholes which makes sense of the forming of the parts. Which is the issue I am focused on. -
Thoughts on EpistemologyThe time wasting is apparently mutual. IF it is all a matter of degree, then there can be no absolutely private language...
I think we agree, but you do not realise it. Odd. — Banno
Tiresome bullshit. The corollary was that public language is equally a matter of degree.
Are you wanting to say there can be no absolutely public language?
So still the same old games from you, Banno. The less you say, the safer you feel. It's a life I guess.
apokrisis

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum