-
 hypericin
2.1kFrom an excellent clickbait article by Scientific American:
hypericin
2.1kFrom an excellent clickbait article by Scientific American:
The problem vexing the minds of experts is as follows: Sleeping Beauty agrees to participate in an experiment. On Sunday she is given a sleeping pill and falls asleep. One of the experimenters then tosses a coin. If “heads” comes up, the scientists awaken Sleeping Beauty on Monday. Afterward, they administer another sleeping pill. If “tails” comes up, they wake Sleeping Beauty up on Monday, put her back to sleep and wake her up again on Tuesday. Then they give her another sleeping pill. In both cases, they wake her up again on Wednesday, and the experiment ends.
The important thing here is that because of the sleeping drug, Sleeping Beauty has no memory of whether she was woken up before. So when she wakes up, she cannot distinguish whether it is Monday or Tuesday. The experimenters do not tell Sleeping Beauty either the outcome of the coin toss nor the day.
They ask her one question after each time she awakens, however: What is the probability that the coin shows heads?
I suggest you read the full article. Its a curious problem, seemingly too simple to still be in dispute.
What do you think?
At first I was a confident halfer, and I was about to post as such. But then I realized after a little more thought, thirders are correct after all! I think the arguments in the article are sound. Here is another:
Sleeping Beauty is perplexed, and is determined to work out the answer. She consents to repeat the experiment 100 times. She keeps a tally by her bed, with two columns, one marked "Heads", the other marked "Tails". Every time she wakes up, she looks at the coin, and adds a mark to the correct column. At the end of the experiment, it turns out that the coin came up 50 times for each side. Looking at her tally, Sleeping Beauty sees 50 marks under Heads, and 100 marks under Tails. She thereby concludes, if she had been asked the question and replied "heads" every time, she would have been correct 1/3 of the times.
Edit: I'm back to 1/2
Edit2: Back to 1/3 again! I think this is where I will stay.
Edit3: Sigh. Back to 1/2-
What is the answer? 1/260%1/336%other4%
-
What is the answer?
-
 noAxioms
1.7kThe basic test is if SB places a bet each time. She makes money (does not break even) if she bets on tails. This is pretty easy to work out.
noAxioms
1.7kThe basic test is if SB places a bet each time. She makes money (does not break even) if she bets on tails. This is pretty easy to work out.
If the experiment is done twice (one heads, one tails), she sees heads once and tails twice. That sounds like 1/3 heads to me.
To emphasize this answer, imagine head: they wake her the once, but tails, they do it 100 times before the experiment ends. The coin flip odds are still 50/50, but the odds that on a random waking she sees tails is overwhelming. -
 hypericin
2.1k
hypericin
2.1k
But now I think we are both cheating. The experiment specifically is conducted once, not as many times as we please. That changes everything.
To emphasize this answer, imagine head: they wake her the once, but tails, they do it 100 times before the experiment ends. The coin flip odds are still 50/50, but the odds that on a random waking she sees tails is overwhelming. — noAxioms
Presuming the experiment is conducted multiple times, yes it is overwhelming. But what if it is just conducted once?
The article states this counterargument nicely. Consider this variation:
A 100 sided dice is rolled. If it lands on 100, SB is awakened 1000 times. Otherwise, she is awakened once. On each awakening, is it more likely to be 100 than 1-99 inclusive?? -
 L'éléphant
1.7kI thought I saw this problem posted before in the Lounge?
L'éléphant
1.7kI thought I saw this problem posted before in the Lounge?
Without memory of prior awakening or knowledge of what day it is, she would have to answer 1/2. What SB remembers is she was put to sleep and she awakens. The coin is tossed once in her memory.They ask her one question after each time she awakens, however: What is the probability that the coin shows heads?
I thought the question of the experimenters was directed to SB, not to the readers of the puzzle. -
 jgill
4kI thought I saw this problem posted before in the Lounge? — L'éléphant
jgill
4kI thought I saw this problem posted before in the Lounge? — L'éléphant
Yes. It's been discussed before. It can be considered a problem in decision making.
Sleeping Beauty -
 unenlightened
10k
unenlightened
10k
The Sailor's Child problem, introduced by Radford M. Neal, is somewhat similar. It involves a sailor who regularly sails between ports. In one port there is a woman who wants to have a child with him, across the sea there is another woman who also wants to have a child with him. The sailor cannot decide if he will have one or two children, so he will leave it up to a coin toss. If Heads, he will have one child, and if Tails, two children. But if the coin lands on Heads, which woman would have his child? He would decide this by looking at The Sailor's Guide to Ports and the woman in the port that appears first would be the woman that he has a child with. You are his child. You do not have a copy of The Sailor's Guide to Ports. What is the probability that you are his only child, thus the coin landed on Heads (assume a fair coin)? — wiki
This version looks a lot clearer to me, and the question at the end looks like a deception. 2 possible worlds, contain 3 possible identities. So other things (ie coins) being equal, I am more likely to be one of two than one of one. So P. (only child) is 1/3 notwithstanding P. (heads) is 1/2, because tails is twice as fruitful as heads. -
 Michael
16.8kLet's say that there are three beauties; Michael, Jane, and Jill. They are put to sleep and assigned a random number from {1, 2, 3}.
Michael
16.8kLet's say that there are three beauties; Michael, Jane, and Jill. They are put to sleep and assigned a random number from {1, 2, 3}.
If the coin lands heads then 1 is woken on Monday. If the coin lands tails then 2 is woken on Monday and 3 is woken on Tuesday.
If Michael is woken then what is his credence that the coin landed heads?
David Lewis' answer, summarised here, states that:
Sleeping Beauty receives no new non-self-locating information throughout the experiment because she is told the details of the experiment. Since her credence before the experiment is P(Heads) = 1/2, she ought to continue to have a credence of P(Heads) = 1/2 since she gains no new relevant evidence when she wakes up during the experiment.
Michael's credence before the experiment is P(1) = 1/3, so if woken he ought to continue to have a credence of P(1) = 1/3 since he gains no new relevant evidence if he wakes up during the experiment.
However, given that if woken he is 1 iff the coin landed heads, he ought to have a credence of either P(Heads) = 1/3 or P(1) = 1/2. -
 hypericin
2.1kI think betting is cheating, and is not actually correlated to the probabilities.
hypericin
2.1kI think betting is cheating, and is not actually correlated to the probabilities.
Bet on heads or tails. If tails, you get to repeat the same bet again, on the same toss
Of course, you would pick tails because you get a bonus if you win. But this doesn't make tails more likely.
What if we let SB bet, but only once. If the probability of heads is really 1/3 on each awakening, then a bet on tails should still be profitable. But it is not. -
 hypericin
2.1kThis version looks a lot clearer to me, and the question at the end looks like a deception. 2 possible worlds, contain 3 possible identities. So other things (ie coins) being equal, I am more likely to be one of two than one of one. So P. (only child) is 1/3 notwithstanding P. (heads) is 1/2, because tails is twice as fruitful as heads. — unenlightened
hypericin
2.1kThis version looks a lot clearer to me, and the question at the end looks like a deception. 2 possible worlds, contain 3 possible identities. So other things (ie coins) being equal, I am more likely to be one of two than one of one. So P. (only child) is 1/3 notwithstanding P. (heads) is 1/2, because tails is twice as fruitful as heads. — unenlightened
Alter the setup:
The sailor had two choices, have sex with a homely fishmaiden of Innsmouth, with whom he could only bear 1 coupling, or visit the Siren of Fertility, whereupon he knows he will sire 10 sprats. Feeling queasy about such a paternal burden, he flips 2 coins: He will only visit the siren if both coins are heads.
You are given a bet: Guess your mother correctly, and win your father's treasure, a giant sack of doubloons. Which would you choose? -
 hypericin
2.1k
hypericin
2.1k
I don't think they do. Extend the numbers out to a ridiculous amount: the sailor flipped 12 coins, and fathers 10000 with the Siren. Would you wager the giant sack that dad flipped 12 heads?
Seriously, put yourself in that position. A giant sack of gold coins, but you have to choose correctly.
If you chose The Siren, you would feel like The World's Idiot for the rest of your life.
The argument for The Siren only works if you repeat this setup multiple times. Even though the Siren is much more unlikely, she more than makes up for it when she is selected with her ultra fecundity. So, if there were a million trials, and you were one of all those lives, you should pick The Siren. But this doesn't work at all with just one trial.
(and BTW, frankly speaking you have kind of a horse face) -
 unenlightened
10kIf you chose The Siren, you would feel like The World's Idiot for the rest of your life. — hypericin
unenlightened
10kIf you chose The Siren, you would feel like The World's Idiot for the rest of your life. — hypericin
Not if I was right. The odds that I uniquely am the sailors lovely frog daughter are surely very small indeed if it is a unique occurrence. It is as unlikely as that a frog should be mistaken for a horse. And that is my gamble, not the one my father made. -
 Michael
16.8kThe number assignment and the coin toss do not affect each other, and so they are independent events.
Michael
16.8kThe number assignment and the coin toss do not affect each other, and so they are independent events.
But there is something different about my example. If we use Bayes' theorem then:
Given that P(Heads|Awake) ≠ P(Heads), waking does in fact provide new relevant evidence. And the above shows that the correct answer is 1/3.
Applying this same formula to the original problem gives P(Heads|Awake) = P(Heads), and so is consistent with Lewis' reasoning and his conclusion that the correct answer is 1/2.
-
 hypericin
2.1k
hypericin
2.1k
How would you respond to this:
This formula makes no mention of the possibility of waking up on Tuesday. If we told SB when she woke up, "It is Monday", she could use this reasoning, and come up with the correct answer of 1/2.
But then suppose we didn't tell her anything. This reasoning works for the case of Monday, and gives 1/2. But there is an unaccounted for possibility that it is Tuesday. And if so, the probability of heads is 0.
So therefore, the correct answer cannot be 1/2, it must be less, since 1/2 is the Monday-only answer, which doesn't factor in the possibility of it being Tuesday. -
 hypericin
2.1kI have finally solved this thing. I am now 100% convinced 1/3 is correct, and everyone who answered the poll except for me is wrong.
hypericin
2.1kI have finally solved this thing. I am now 100% convinced 1/3 is correct, and everyone who answered the poll except for me is wrong.
There are three possible waking events.
A. Heads, Monday
B. Tails, Monday
C. Tails, Tuesday
To answer correctly, sleeping beauty must evaluate the probability she is experiencing each of these events.
1: P(A) = P(B): If heads, A happens, if tails, B happens
2: P(A) = P(C): If heads, A happens, if tails, C happens
3: P(B or C) = 2P(A): The combined probability of B and C must be twice the probability of A
4: P(A) = P(Heads) = 1/3 -
 Michael
16.8kA variation of my variation.
Michael
16.8kA variation of my variation.
Let's say that there are two beauties; Michael and Jane. They are put to sleep and assigned a random number from {1, 2}.
If the coin lands heads then 1 is woken on Monday. If the coin lands tails then 2 is woken on Monday and Tuesday.
If Michael is woken then what is his credence that the coin landed heads?
If we use Bayes' theorem then:
-
 Michael
16.8kHere's a Venn diagram to show how the probabilities interlink (where "Monday" should be read as "she will be woken on Monday" and "Tuesday” as "she will be woken on Tuesday"):
Michael
16.8kHere's a Venn diagram to show how the probabilities interlink (where "Monday" should be read as "she will be woken on Monday" and "Tuesday” as "she will be woken on Tuesday"):
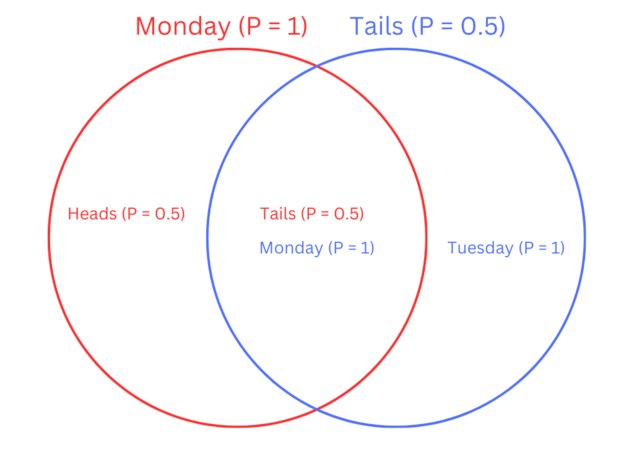
The probability that the coin will land heads and she will be woken on Monday is 1/2.
The probability that the coin will land tails and she will be woken on Monday is 1/2.
The probability that the coin will land tails and she will be woken on Tuesday is 1/2.
As the Venn diagram shows, there are two (overlapping) probability spaces, hence why the sum of each outcome's probability is greater than 1. -
 L'éléphant
1.7k
L'éléphant
1.7k
She can't. The instruction reads that she has no memory of prior awakening or what day it is. She doesn't even know that the experimenter tosses the coin, because they do it when she's put back to sleep. The question to her is "what are the odds that a coin will land heads (or tails)". Since she must know what a coin is, and what heads and tails is, she must answer "1/2".To answer correctly, sleeping beauty must evaluate the probability she is experiencing each of these events. — hypericin
The sleeping pills, the day she awakens, and other conditions included in the instruction are all distractions for you or me or others who are reading the puzzle to divert our attention from the correct answer.
Edit: the correct answer is 1/2 when the coin is tossed once. All SB knows is the coin is tossed once, and her information is purely coming from the question. -
 hypericin
2.1kThe probability that the coin will land heads and she will be woken on Monday is 1/2.
hypericin
2.1kThe probability that the coin will land heads and she will be woken on Monday is 1/2.
The probability that the coin will land tails and she will be woken on Monday is 1/2.
The probability that the coin will land tails and she will be woken on Tuesday is 1/2. — Michael
This is straightforwardly true, but from the perspective of an observer of the experiment. But to answer the problem you must adopt SB's perspective. That makes all the difference.
We all know the odds of flipping a coin. But SB is asked on every wakening, and is woken twice as much on tails. This must influence the odds, in the same way that
Bet on heads or tails. If tails, you get to repeat the same bet again, on the same toss — hypericin
Influences the gambling odds, even though the coin toss is fair in both cases -
 Michael
16.8kThis is straightforwardly true, but from the perspective of an observer of the experiment. But to answer the problem you must adopt SB's perspective. That makes all the difference. — hypericin
Michael
16.8kThis is straightforwardly true, but from the perspective of an observer of the experiment. But to answer the problem you must adopt SB's perspective. That makes all the difference. — hypericin
Why does it make a difference?
But SB is asked on every wakening, and is woken twice as much on tails. This must influence the odds — hypericin
Why would it influence the odds?
Let's say that I wanted to bet on a coin toss. I bet £100 that it will be tails. To increase the odds that it's tails, I ask you to put me to sleep, wake me up, put me back to sleep, wake me up, put me back to sleep, wake me up, and so on. Does that make any sense?
Influences the gambling odds, even though the coin toss is fair in both cases — hypericin
It doesn't influence the odds. You just get to bet twice, hence twice the payout. -
 hypericin
2.1kLet's say that I wanted to bet on a coin toss. I bet £100 that it will be tails. To increase the odds that it's tails, I ask you to put me to sleep, wake me up, put me back to sleep, wake me up, put me back to sleep, wake me up, and so on. Does that make any sense? — Michael
hypericin
2.1kLet's say that I wanted to bet on a coin toss. I bet £100 that it will be tails. To increase the odds that it's tails, I ask you to put me to sleep, wake me up, put me back to sleep, wake me up, put me back to sleep, wake me up, and so on. Does that make any sense? — Michael
I get the intuition. But no, it doesn't make sense, and it it is a poor analogy to the problem.
Here is a much better analogy, that I think is more intuitively clear than this weird experiment:
An idiot runs a gambling website, HeadsOrTails.com . You place a bet, and if you win, the site pays you 97c on the dollar, along with your bet. Behind the scenes, a coin is mechanically flipped in advance, and then users are asked to bet heads or tails based on that flip. But there is an idiosyncrasy: If the coin toss is heads, the site generates one betting prompt for one user. But if it's tails, the site generates two prompts for two users.
Therefore, for every prompt, the coin is twice as likely to be tails as it is heads, because tails generates two prompts, while heads generates one. By asking more questions for one coin side vs the other, the probability at every question is skewed towards the side that gets more questions asked. Therefore t will be profitable to always bet tails, and the site will go bankrupt quickly. -
 Srap Tasmaner
5.2kSuppose you actually did this, as an experiment, just looking for each subject's response.
Srap Tasmaner
5.2kSuppose you actually did this, as an experiment, just looking for each subject's response.
Let's say you have 1200 subjects; one coin toss each, and let's say you get 600 heads and 600 tails. So 600 subjects get a single interview, and 600 get two. Total of 1800 interviews.
How many interviews are conducted, the toss having come up heads? 600.
Then for any given interview, the chances that it's one of the heads interviews are 1 in 3. I think that's all the reasoning you need.
****
If you're inclined to double-check, you might try something like this:
Not perfectly clear what that means though, so let's explicitly take subjects one at a time, something like this:
That looks a little more tractable. Certainly pr(heads(x)) is 1/2 for everyone. If in fact x gets heads, then x is one of the 1800 interviews, so pr(interview(x)) would be 1/1800, and for tails 2/1800. For an "average" subject x, then, the value should be their average (because halves), which is 1.5/1800, or 1/1200. Hey, that looks right! Maybe we needn't have bothered about the heads and tails...
(Is 1/1200 really the right value for pr(interview(x)) -- doesn't it make a difference whether their coin came up heads or tails? Yes and no: what we want here is an absolute probability, not a conditional one, so we deliberately average out the cases to get a baseline, and the result is just what you'd expect. Pick an interview at random, and the chances of it being an interview of a specific subject are, on average, 1 in 1200. Just as we leave pr(heads(x)) at the baseline of 1/2 for everyone.)
What about pr(interview(x) | heads(x))? What does this mean, and how do we assign a value to it? It's the chances that a given interview is of subject x, given that x's toss came up heads. That's the 1/1800 we just looked at.
Now we have values for everything on the right:
That is, given any interview, the chances of the subject of that interview's toss having come up heads are 1 in 3. Exactly the same as above.
SB ought to reason that it's more likely the interview she's currently engaged in is one of the tails interviews, so her credence for heads should be 1/3. -
 Michael
16.8k
Michael
16.8k
Given that the coin flip just determines if a Tuesday interview will happen, Beauty is being asked for her credence that a Tuesday interview will happen.
That she's interviewed twice as often if a Tuesday interview will happen isn't that a Tuesday interview will happen twice as often.
That she's interviewed twice as often if it's tails isn't that it's tails twice as often.
If it helps, consider that the coin toss happens after the Monday interview.
No, I'm in the double halfer camp now. The post right above explains my current thinking.
((This is, I don't know, maybe the third time I've argued with Michael about something and then concluded he was right all along.)) — Srap Tasmaner
So you've switched back to being a thirder? -
 Srap Tasmaner
5.2kSo you've switched back to being a thirder? — Michael
Srap Tasmaner
5.2kSo you've switched back to being a thirder? — Michael
I switched back shortly after that post; it's right there in the thread. The argument that convinced me was this: consider a variation, "Informative SB", in which Beauty is told she will be awakened twice either way, but if it was heads she will be told at the second interview that it was heads and that this is her second interview; at none of the others will she be given such information.
Beauty cannot distinguish between this variation and the actual experiment. This just makes it clear that being interviewed is itself informative and she should condition on it; it amounts to being told "either it was tails or this is your first interview." The likelihood that the coin came up heads is of course 1/2; the likelihood that it came up heads, given that you're asking, the conditional probability, is 1/3.
Let's say that I wanted to bet on a coin toss. I bet £100 that it will be tails. To increase the odds that it's tails, I ask you to put me to sleep, wake me up, put me back to sleep, wake me up, put me back to sleep, wake me up, and so on. Does that make any sense? — Michael
In our version, the base rate of heads interviews is 1 in 3. Make it 1 in 1000. (That is, 999 awakenings on tails, not 2.) Isn't it obvious that if I'm a subject in such an experiment, I know it's far more likely I'm being asked for my credence because my coin came up tails? If I'm one of 1200 subjects, I know there are 600,000 interviews, only 600 of which were for heads, while 599,400 were for tails. Equally likely that this interview is for heads as for tails? Not by a long shot. -
 Michael
16.8kI switched back shortly after that post; it's right there in the thread. The argument that convinced me was this: consider a variation, "Informative SB", in which Beauty is told she will be awakened twice either way, but if it was heads she will be told at the second interview that it was heads and that this is her second interview; at none of the others will she be given such information. — Srap Tasmaner
Michael
16.8kI switched back shortly after that post; it's right there in the thread. The argument that convinced me was this: consider a variation, "Informative SB", in which Beauty is told she will be awakened twice either way, but if it was heads she will be told at the second interview that it was heads and that this is her second interview; at none of the others will she be given such information. — Srap Tasmaner
I don't understand how this is different to the original. In the original she's woken up on Wednesday and told the result of the coin flip (whether heads or tails). So there are two interviews if heads, three interviews if tails. -
 Srap Tasmaner
5.2k
Srap Tasmaner
5.2k
The point of the variation is that she is told something will happen only at the second heads interview. Fill in whatever you like, it will be missing from the others and from all of the interviews in stock SB. The absence of that thing is informative, it amounts to "it was tails or this is your first interview," and this is true as well for stock SB. Being asked is itself information you can condition on. -
 Michael
16.8kThe absence of that thing is informative, it amounts to "it was tails or this is your first interview," and this is true as well for stock SB. Being asked is itself information you can condition on. — Srap Tasmaner
Michael
16.8kThe absence of that thing is informative, it amounts to "it was tails or this is your first interview," and this is true as well for stock SB. Being asked is itself information you can condition on. — Srap Tasmaner
How do you condition on such a thing? What values do you place into Bayes' theorem?
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum








