-
 JeffJo
175
JeffJo
175
No.As I understand it, your proposal is essentially the principle of indifference applied to a sample space that isn't the same as the stated assumptions of the SB problem, namely your sample space is based on the triple
{Coin,Day,Wakefulness}
upon which you assign the distribution Pr(Heads,Monday,Awake) = Pr(Tails,Monday,Awake) = Pr(Heads,Tuesday,Asleep) = Pr(Tails,Tuesday,Awake) = 1/4. — sime
The reason I keep asking for specific answers to specific questions, is that I find that nobody addresses "my sample space." Even though I keep repeating it. They change it, as you did here, to include the parts I am very intentionally trying to eliminate.
There are two, not three, random elements. They are COIN and DAY. WAKE and SLEEP are not random elements, they are the consequences of certain combinations, the consequences that SB can observe.
There are two sampling opportunities during the experiment, not two paths. The random experiment, as it is seen by SB's "inside" the experiment, is just one sample. It is not one day on a fixed path as seen by someone not going through the experiment, but one day only. Due to amnesia, each sample is not related, in any way SB can use, to any other.
Each of the four combinations of COIN+DAY is equally likely (this is the only application of the PoI), in the prior (this means "before observation") probability distribution. Since there are four combinations, each has a prior ("before observation") probability of 1/4.
In the popular problem, SB's observation, when she is awake, is that this sample could be H+Mon, T+Mon, or T+Tue; but not H+Tue. She knows this because she is awake. One specific question I ask, is what happens if we replace SLEEP with DISNEYWORLD. Because the point that I feel derails halfers is the sleep.
Halfers seem to think SLEEP means H+Tue cannot be sampled. So, I change the problem so it can be sampled. SB's observation is now that she is in an interview. So this sample could be H+Mon, T+Mon, or T+Tue; but not H+Tue. She knows this because she is in an interview, not at DisneyWorld. There is no difference it her utilization of the mechanics of the experiment, nor of what her observation means.
This probability space includes a distribution says that a single sampling is happening on two days at the same time. Halfers convince themselves that there is no contradiction; after TAILS the "other" awakening is identical, and after HEADS it is not observed. But that doesn't work if we change to DISNEYWORLD.By contrast, the probability space for the classical SB problem is that of a single coinflip C = {H,T}, namely (C,{0,H,T,{H,T}},P) where P (C = H) = 0.5 .
What is non-permitted? It is a functionally equivalent one. Consequence #1 occurs with three of the four combinations, and Consequence #2 occurs with the fourth. The question is only asked with Consequence #2. I'm sorry, but this is a rationalization.But what makes your argument incorrect [is] the use of a non-permitted sample space.
But its use is why I asked the specific question about my Camp Sleeping Beauty version. There is a 6x6 calendar for the six days of camp, and a six-sided die is used to pick one row (the columns are days of the week). If campers partake of, say, activity C then how do we deduce the conditional probability that the die roll was, say, 5?
I claim that the 36 cells each have a prior probability of 1/36 (PoI again). And that the conditional probability of a 5, given activity C, is the number of times C appears in row 5, divided by the number of times C appears in the calendar.
AND, this does not, and cannot, change if one of the "activities" is "sleep through the entire day." This is what addresses you concern here, and I'd love to hear why D="DARTS" produces a different result than D="DOZE."
There is nothing "non-permitted" about including either D in the sample space. In fact, since either D is part of the camp counselors' planning, they must be functionally equivalent. And it applies to any NxN isomoprhic experiment, even if N=2.
We could discuss this conclusion, but that discussion will need to include answers. -
 sime
1.2kThe reason I keep asking for specific answers to specific questions, is that I find that nobody addresses "my sample space." Even though I keep repeating it. They change it, as you did here, to include the parts I am very intentionally trying to eliminate. — JeffJo
sime
1.2kThe reason I keep asking for specific answers to specific questions, is that I find that nobody addresses "my sample space." Even though I keep repeating it. They change it, as you did here, to include the parts I am very intentionally trying to eliminate. — JeffJo
I think you misunderstand me. I am simply interpreting the thrux of your position in terms of an extended sample space. This isn't miscontruing your position but articulating it in terms of Bayesian probabilities. This step is methodological and not about smuggling in new premises, except those that you need to state your intuitive arguments, which do constitute additional but reasonable premises. [/quote]
There are two, not three, random elements. They are COIN and DAY. WAKE and SLEEP are not random elements, they are the consequences of certain combinations, the consequences that SB can observe. — JeffJo
Look at this way: It is certainly is the case that according to the Bayesian interpretation of probabilities, one can speak of a joint probability distribution over (Coin State, Day State, Sleep State), regardless of one's position on the topic. But in the case of the frequentist halfer, the sleep-state can be marginalised out and in effect ignored, due to their insistence upon only using the coin information and rejecting counterfactual outcomes that go over and above the stated information.
There are two sampling opportunities during the experiment, not two paths. The random experiment, as it is seen by SB's "inside" the experiment, is just one sample. It is not one day on a fixed path as seen by someone not going through the experiment, but one day only. Due to amnesia, each sample is not related, in any way SB can use, to any other. — JeffJo
You have to be careful here, because you are in danger of arguing for the halfers position on their behalf. Counterfactual intuitions, which you are appealing to below, are in effect a form of path analysis, even if you don't see it that way.
Each of the four combinations of COIN+DAY is equally likely (this is the only application of the PoI), in the prior (this means "before observation") probability distribution. Since there are four combinations, each has a prior ("before observation") probability of 1/4.
In the popular problem, SB's observation, when she is awake, is that this sample could be H+Mon, T+Mon, or T+Tue; but not H+Tue. She knows this because she is awake. One specific question I ask, is what happens if we replace SLEEP with DISNEYWORLD. Because the point that I feel derails halfers is the sleep. — JeffJo
But the Sleeping Beauty Problem per-se does not assume that the Sleeping Beauty exists on tuesday if the coin lands heads, because it does not include an outcome that measures that possibility. Hence you need an additional variable if you wish to make your counterfactual argument that SB would continue to exist on tueday in the event the coin lands heads. Otherwise you cannot formalise your argument.
Just to clarify, I'm not confusing you for a naive thirder, as I mistook you for initially, where i just assumed that you were blindly assigning a naive prior over three possible outcomes. I think your counterfactual arguments are reasonable, and I verified that they numerally check out; but they do require the introduction of a third variable to the sample space in order to express your counterfactual intuition that I called "sleep state" (which you could equally call "the time independent state of SB"). -
 JeffJo
175
JeffJo
175
You are inserting details into the description of the outcomes, that provide no additional information. It has nothing to do with the [crux? thrust?] of my position. You are obfuscating the sample space in order to suggest an omission.I am simply interpreting the thrux of your position in terms of an extended sample space. — sime
Look at it this way: a sample space is a set of distinct outcomes that include all possibilities. An event is a set of outcomes. These concepts often get confused. You are confusing them, by including the name of an event (awake, asleep), as your "new variable" that you claim helps to define the outcome.
There is a simple model for how SB views each waking in an NxN sleeping-beauty calendar. There are N^2 cells in the calendar. Each has an N^(-2) prior probability at the start of an amnesia'ed day, before SB is awakened. When an awake SB observes activity X, her credence in any row or column of the calendar is the number of times activity X occurs in that row or column, divided by the number of times it occurs in the entire calendar.
The only complication in this model, is what happens when one of the activities does not permit an observation. But since the crux of SB's observation is recognizing the activities that did not happen, that cannot be an issue. For there to be an effect, that calendar cell has to cease to exist, not be unobservable. So I'm trying to get that difference addressed.
That's just rationalization. I have proposed a model, that I claim represents the SB problem. Whether or not it is "smuggling in new premises" (it isn't, it is extending a premise that already exists), the issues here are only (A) Is the SB problem an example of my model, (B) does my solution apply to the model in general, and (C) how does an unobservable activity affect the solution.This step is methodological and not about smuggling in new premises, except those that you need to state your intuitive arguments, which do constitute additional but reasonable premises.
In other words, when you claim that I am "smuggling in a new premise" you are looking at the changes I suggest add details. What I am trying to get you to address is how the SB problem is an example of my model with fewer details.
Look at this way: It is certainly is the case that according to the Bayesian interpretation of probabilities, one can speak of a joint probability distribution over (Coin State, Day State, Sleep State), regardless of one's position on the topic.
What you are doing is creating an event, a subset of the sample space, and applying it as a "new variable" in every outcome member of that event. If you were adding new descriptors, you should add all to each outcome. Yes, some will end up with zero probability, like H+Tue+Awake.
And you confuse "measuring the possibility" with "the possibility exists as an outcome." But I devised specific questions to address this exact issue, which have gone completely ignored.But the Sleeping Beauty Problem per-se does not assume that the Sleeping Beauty exists on tuesday if the coin lands heads, because it does not include an outcome that measures that possibility.
- If were to wake SB on H+Tue, and take her to DisneyWorld (see how I don't need to add DISNEYWORLD asa descriptor in the sample space?), what is her credence in the event (H+Mon or H+Tue) if she observes the event (H+Mon or T+Mon or T+Tue)? It is:
- Pr(((H+Mon or H+Tue) and (H+Mon or T+Mon or T+Tue)) / Pr(H+Mon or T+Mon or T+Tue)
- = Pr(H+Mon) / Pr(H+Mon or T+Mon or T+Tue) = (1/4)(/(3/4) = 1/3.
Except, you didn't add one. You applied a name that always applies to combination of the other variables. And pardon me for suggesting this, but it seems you are using it to not address my very specific questions, that your "new variable" adds nothing to. If you think it does, then use it as part of your answer to those questions.[You] do require the introduction of a third variable to the sample space in order to express your counterfactual intuition that I called "sleep state" (which you could equally call "the time independent state of SB").
And it is not "counterfactual." The outcome H+Tue can occur. The prior sample space is comprises every possibility before the random elements are determined, and before an observation is made. And I'm tired of all this repetition, but all this can be explored by addressing the questions I have asked. -
 sime
1.2k
sime
1.2k
All I can say is that we aren't agreeing as to the semantics of the problem. Your sample space includes the counterfactual possibility (H, Tuesday), which isn't in the sample space of the experiment as explicitly defined. You appeal to "if we awoke SB on tuesday on the event of heads" might be a perfectly rational hypothetical in line with common-sense realism, but that hypothetical event isn't explicit in the problem description. Furthermore, the problem is worded as a philosophical thought experiment from the point of view of SB as a subject who cannot observe that tuesday occurred on a heads result, nor even know of her previous awakenings, in sharp contrast to an external point of view relative to which her awakenings are distinguishable and for which the existence of tuesday isn't conditional on the outcome of the event of tails.
As straw-clutching as this might sound, there are radically minded empiricists who would argue that the existence of "tuesday" for the sleeping beauty is contingent upon her being awake. For such radical empiricists the event (H,Tuesday) doesn't merely have zero probability, but is a logical contradiction from SB's perspective.
Epistemically for SB,
(h,mon) -> observable, but undiscernable.
(h,tue) - > unobservable.
(t,mon) -> observable but undiscernible.
(t,tue) -> observable but undiscernible.
So we are back to the question as to whether (h,tue) should be allowed in the sample space. This is ultimately what our dispute boils down to. -
 JeffJo
175
JeffJo
175
So, are you saying that the week skips from Monday to Wednesday if the coin lands on Heads? What it they wait to flip the coin until Tuesday Morning?All I can say is that we aren't agreeing as to the semantics of the problem. Your sample space includes the counterfactual possibility (H, Tuesday), which isn't in the sample space of the experiment as explicitly defined. — sime
As I have described in several ways, and constructed questions to test, the experiment consists of two days, with two COIN+DAY potential-observation methods. But the amnesia means only one is "seen" at a time, and prevents them from being connected (for Pierre: this means no path information). But H+Tue, with no indication of waking or sleeping, is still a possibility, and a sample space must describe all possibilities.
Please, what is inconsistent about it, when we ignore whether she is awake? Do you think she does not know it can happen?You appeal to "if we awoke SB on tuesday on the event of heads" might be a perfectly rational hypothetical...
Why does the problem description have to explicitly say that something which obviously can happen, can actually happen? The description only says that SB will sleep through it, not that it is excluded from the realm of possibility.But that hypothetical event isn't explicit in the problem description.
But again, look at the version where, on H+Tue, SB is left asleep with probability Q and otherwise taken to DisneyWorld. The original problem is a sub-case of this with Q=0. the one you think is a different problem, but is not, has Q=1. Instead of thinking of me adding something, address this one as Q approaches, and then equals, 0.
But who still knows it can happen. All I'm saying is that your "philosophical thought experiment" does not "philosophically eliminate Tuesday from the week" if the coin lands Heads.Furthermore, the problem is worded as a philosophical thought experiment from the point of view of SB as a subject who cannot observe that tuesday occurred on a heads result,
OR. we could just go back to the problem that spawned the SB problem, which was more of that "philosophical thought experiment."
- SB is put to sleep on day 0.
- A fair coin is flipped, and an N-sided die is rolled.
- Over the next N days, SB is woken, or not, based on what is currently showing on the coin and die.
- If she is woken, she is amnesia-ed before going back to sleep that night.
- Regardless of whether she is woken, the die is rotated down by 1 (resetting to N if it was a 1).
The conditions for waking her are if the coin is currently showing Heads, or the die is currently showing 1.
In this version, an exact implementation of the problem proposed by Arnold Zuboff, SB knows FOR A FACT that the experimenters look at the coin and die this morning. She knows, ALSO FOR A FACT, the there were 2*N equally-likely combinations they could have seen on this particular day. She knows, AGAIN FOR A FACT that she would not be awake for N-1 of them, she would be awake for N+1, and in only one of those is the coin showing HEADS. Her credence in Heads is 1/(N+1).
If you think I changed something by adding (if N>2) more days, or that changing the order makes it different, please explain how instead of avoiding the issue by simply saying it is. If you think SB knowing that some combinations could not be observed means that they must be excluded from the sample space, consider that she could be awoken on all days, observe the coin and die herself, and then a sleep+amnesia gas it released if she sees HEADS and DIE>1. -
 JeffJo
175An N-day experiment:
JeffJo
175An N-day experiment:
- The days of the experiment are named D(1) through D(N).
- D(0) is the night before the experiment begins, when SB is informed of all these details before going to sleep.
- After she goes to sleep on D(0), an M-sided die will be rolled and preserved throughout out the experiment.
- What occurs on each day of the experiment is predetermined using an M-row by N-column calendar. One of M distinct activities (that can all be differentiated from each other), A(1) through A(M), is assigned to each cell in the calendar, such that each appears at least once. The calendar is shown to SB on D(0).
- With one variation about A(M) that will be explained below, SB will be awakened each day, and will participate in the activity assigned to that day's column and the row determined by the die roll.
- After participating in a day's activity, except A(M), SB will be shown the calendar and asked for her credence in each possible die roll. After any waking activity, she will be put back to sleep with amnesia.
There are three possibilities for the variation:
- For A(M), SB will be left asleep all day.
- For A(M), SB will be taken to DisneyWorld.
- For A(M), SB will be left asleep with probability 0<Q<1 or else taken to DisneyWorld.
After participating activity A(m), for 1<=m<M, what should SB's credence for any die roll d be? I say that it is the number of times A(m) appears in row d, divided by the number of times it appears in the calendar. I say that it does not depend, in any way, on which variation is used.
The popular SB problem is a version of this with M=N=2 and using variation #1. A(1) is simply "interview" and appears in every cell except the HEADS row and the Tuesday column. So the answer, when she is interviewed, is that Pr(HEADS|INTERVIEW)=1/3.
The extra details DO NOT make this problem's solution inapplicable to the popular SB problem. In fact, any solution to the popular one has to be consistent with this problem's solution. All the added details do is illustrate why various rationalizations made by halfers, to avoid using simple conditional probability methods,are invalid. In particular, the three variations for A(M) are meant to show how A(M) cannot affect the solution.
I've been trying to get many questions answered for about a month now, and non have been addressed, except with unsupported assertions that I must be wrong. If that is true, there must be a solution to this problem I present today that differs from what I said.
If you disagree, please provide a solution to this problem, with specific detail about how the three variations affect the answer, not just an assertion that they must. -
 Michael
16.6kIn summary, rational credence doesn’t float free of betting; it aligns with whatever gets checked. If we check one answer per run, rational calibration yields 1/2. If we check one answer per awakening, rational calibration yields 2/3 (or 6/11 in the die case). The same coin is being talked about, but the Halfer and Thirder interpretations of SB’s credence refer to different scorecards. Given one scorecard and one payout structure, everyone agrees on the rational betting strategy in normal cases. — Pierre-Normand
Michael
16.6kIn summary, rational credence doesn’t float free of betting; it aligns with whatever gets checked. If we check one answer per run, rational calibration yields 1/2. If we check one answer per awakening, rational calibration yields 2/3 (or 6/11 in the die case). The same coin is being talked about, but the Halfer and Thirder interpretations of SB’s credence refer to different scorecards. Given one scorecard and one payout structure, everyone agrees on the rational betting strategy in normal cases. — Pierre-Normand
In both cases one's credence in the outcome of the coin toss is . We use this credence, in conjunction with the payout structure, to determine which betting strategy has the greater expected return, which is one's credence in the outcome multiplied by the reward multiplied by the number of bets one can make given that outcome.
Single bet before being put to sleep with option to change after being woken up
Independent bets after being woken up
We even perform these calculations before being put to sleep, and so have already determined our betting strategy. Being put to sleep and woken up changes nothing.
You certainly shouldn't perform these calculations after being woken up:
Although the ratio is correct, the actual values are very wrong.
The mistake I think you continue to make is to conflate "the expected return if I always bet on Tails is twice the expected return if I always bet on Heads" and "my credence that the coin landed on Tails/that this is a Tails awakening is twice my credence that the coin landed on Heads/that this is a Heads awakening".
I’ll address your extreme case separately, since it appeals to different (nonlinear) subjective utility considerations. — Pierre-Normand
The logic of the extreme case is the same as the simple case. It doesn't matter if the die has two sides and we're woken twice if it lands on a 1 (and once otherwise) or if it has 2100 sides and we're woken 2101 times if it lands on a 1 (and once otherwise). Given that the experiment is only performed once, no rational person's credence in the outcome of the die roll (or the "type" of awakening one is in) should be determined by the ratio of awakenings in the long run. I think this is self-evident in the extreme case, and this reasoning must also hold in the simple case, else you'd have to argue that the logic changes when the number of sides is >= some which is prima facie absurd. -
 JeffJo
175An N-day experiment:
JeffJo
175An N-day experiment:
The days of the experiment are named D(1) through D(N).
D(0) is the night before the experiment begins, when SB is informed of all these details before going to sleep.
After she goes to sleep on D(0), an M-sided die will be rolled and preserved throughout out the experiment.
What occurs on each day of the experiment is predetermined using an M-row by N-column calendar. One of M distinct activities (that can all be differentiated from each other), A(1) through A(M), is assigned to each cell in the calendar, such that each appears at least once. The calendar is shown to SB on D(0).
With one variation about A(M) that will be explained below, SB will be awakened each day, and will participate in the activity assigned to that day's column and the row determined by the die roll.
After participating in a day's activity, except A(M), SB will be shown the calendar and asked for her credence in each possible die roll. After any waking activity, she will be put back to sleep with amnesia.
There are three possibilities for the variation:
For A(M), SB will be left asleep all day.
For A(M), SB will be taken to DisneyWorld.
For A(M), SB will be left asleep with probability 0<Q<1 or else taken to DisneyWorld. — JeffJo
I'm assuming that nobody can answer this is a way that is consistent with the canonical halfer answer.
Within the subject's knowledge, her waking experience is a random sampling of a certain number of possible combinations of a random integer within a range, and the day within the schedule. The combinations are all equally likely in the prior, but the rules of the experiment limit her waking to a subset of these combinations. Her "new information" is the subset that is consistent with what happens in this waking. The probability of each random number is the size of this intersection of this subset with that number, divided by the size of the subset. -
 Michael
16.6k
Michael
16.6k
If Monday is tennis and Tuesday is football then waking up and playing either tennis or football is new information that allows you to rule out one possibility: if you play tennis then you can rule out that today is Tuesday and if you play football then you can rule out that today is Monday.
You can't rule out that today is Monday or that today is Tuesday before playing either tennis or football, which is why your example is a false analogy. -
 JeffJo
175You can't rule out that today is Monday or that today is Tuesday before playing either tennis or football, which is why your example is a false analogy. — Michael
JeffJo
175You can't rule out that today is Monday or that today is Tuesday before playing either tennis or football, which is why your example is a false analogy. — Michael
So you are saying that if everything is the same as in the popular version but SB plays tennis before the interviews, that her credence is 1/3? But if the activity is "free day," it should be 1/2?
I'm sorry, but you seem to be confused about the problem. There is nothing false about the analogy. -
 Michael
16.6k
Michael
16.6k
If she is interviewed before playing football her credence that the coin landed on tails is not 1, but if she is interviewed after playing football her credence that the coin landed on tails is 1.
Playing football is additional information, but nothing like that is available in the traditional problem, and so your example is a false analogy. -
 JeffJo
175If she is interviewed before playing football her credence that the coin landed on tails is not 1, but if she is interviewed after playing football her credence that the coin landed on tails is 1.
JeffJo
175If she is interviewed before playing football her credence that the coin landed on tails is not 1, but if she is interviewed after playing football her credence that the coin landed on tails is 1.
Playing football is additional information, but nothing like that is available in the traditional problem, and so your example is a false analogy. — Michael
You can't call it a "false analogy" if you don't actually address the analogy. Which you didn't. The point of asking a question is to get an answer to that question, not to have you re-arrange it to get an answer that avoids the question as asked.
So please, address the one with a random number selected from [1,M], M activities, and N days. The activities are distributed over an MxN calendar, with the one limitation that each activity appear at least once. And please note that an "activity" can be "just wake her up" or "don't wake her up." Finally, asking for a credence before the activity was not in my question, so it is irrelevant. But it doesn't break the analogy if you try it - there are just two activities on each waking day. One is "just wake her up" and one might be "tennis" or "football." Just not in your very, very specific distribution, in any distribution.
And yes, it is a proper analogy. The popular problem has M=N=2, A(1)="just wake her up," and A(2)="don't wake her up." A(1) is assigned to three cells in the 2x2 array, and A(2) is assigned to the fourth, Heads+Tuesday.
"New information" is an informal expression in probability theory. It does not mean "something not known before." That's a misrepresentation halfers use as an attempt to justify their answer. It means information about potential outcomes that eliminates some. The sample space is represented by the calendar in my question. Activity A(1) eliminates Heads+Tuesday, and so it is "new information." -
 Michael
16.6k
Michael
16.6k
It's a false analogy because "not being woken up" is nothing like "playing football". It's a mistake to consider "Heads + Tuesday" at all. We can simplify the experiment as such:
1. On Sunday, Sleeping Beauty is put to sleep
2. A coin is flipped
3. On Monday, Sleeping Beauty is woken up and asked her credence that the coin landed on heads
4. If the coin landed on heads then Sleeping Beauty is told the outcome and the experiment ends
5. If the coin landed on tails then Sleeping Beauty is put back to sleep
6. On Tuesday, Sleeping Beauty is woken up and asked her credence that the coin landed on heads
7. Sleeping Beauty is told the outcome and the experiment ends
Her credence when asked is .
This is even more obvious when we replace the coin with a 2100-sided die. If it lands on a 1 then she is woken 2101 times, otherwise she is woken once. After being woken up she is asked her credence that the die landed on a 1. The experiment is not repeated.
Halfers say that her credence is and Thirders say that her credence is . I think any reasonable person would agree with the Halfer. -
 JeffJo
175It's a false analogy because "not being woken up" is nothing like "playing football". It's a mistake to consider "Heads + Tuesday" at all. We can simplify the experiment as such: — Michael
JeffJo
175It's a false analogy because "not being woken up" is nothing like "playing football". It's a mistake to consider "Heads + Tuesday" at all. We can simplify the experiment as such: — Michael
It is true, because the information is what can happen on this day and days like it, vs. what can happen on other days that is different. It is true, because the model can be used to represent the experiment as you described it (and we all understand).
Her credence when asked is 1/3, because of the four possible cells in the 2x2 array, one is eliminated and only one of the remaining three is Heads. -
 Michael
16.6k
Michael
16.6k
As above, replace the coin with a 2100-sided die. If it lands on a 1 then you are woken up on 2101 days otherwise you are only woken up on one day. After being woken up you are asked your credence that the die landed on a 1. The experiment is not repeated.
If you follow your reasoning then you have to claim that your credence is . You believe that the die most likely landed on a 1. I take this as a reductio ad absurdum against your reasoning. It's a fallacy to think of the problem as being represented by a matrix. Not being woken up isn't an "activity" comparable to playing football, hence why it's a false analogy.
If this were to happen to me my credence would be . The die almost certainly didn't land on a 1. -
 Michael
16.6k
Michael
16.6k
It wasn't a typo.
Given a 2100-sided die there are 2100 rows, and given that there are 2101 days there are 2101 columns. That gives us a 2100 × 2101 matrix, i.e. 2201 cells.
The "die rolled a 1" row has 2101 cells where I'm awake. Each other row has 1 cell where I'm awake.
So in total there are 2101 + 2100 - 1 cells where I'm awake. of these cells appear on the "die rolled a 1" row. Therefore, according to your reasoning, after waking up your credence that the die rolled a 1 is . -
 Pierre-Normand
2.9kAlthough the ratio is correct, the actual values are very wrong. — Michael
Pierre-Normand
2.9kAlthough the ratio is correct, the actual values are very wrong. — Michael
Why are you saying the values are wrong? Since there are one and a half awakenings on average per run, it's to be expected that the EV of a single bet placed on any given awakening be exactly two thirds of the EV of a bets placed on any given run.
The mistake I think you continue to make is to conflate "the expected return if I always bet on Tails is twice the expected return if I always bet on Heads" and "my credence that the coin landed on Tails/that this is a Tails awakening is twice my credence that the coin landed on Heads/that this is a Heads awakening".
I am not conflating the two. I am rather calculating the EV in the standard way by calculating the weighed sum of the payouts, where the payout of each potential occurrence is weighted by its respective probability (i.e. my credence in that occurrence being actual). I am pointing out that both the Halfer interpretation of SB's credence (that tracks payouts/awakenings) and the Thirder interpretation (that tracks payouts/runs) of SB's credence yield the exact same EV/run (and they also yield the same EV/awakening) and hence Halfer and Thirders must agree on rational betting strategies despite favoring different definitions of what constitutes SB's "credence". -
 JeffJo
175
JeffJo
175
Then it was a misunderstanding that, if I may be bold, has all the appearance of being a misrepresentation of what you don't want to see if it would support my argument. So I will have to explain it, again, in excessive detail.It wasn't a typo. — Michael
2^101? Where did that come from?Given a 2^100-sided die there are 2^100 rows, and given that there are 2^101 days there are 2^101 columns. That gives us a 2^100 × 2^101 matrix, i.e. 2^201 cells.
As I have stated several times, with an M-sided die, and an N-day[1] experiment, you set up an M-row by N-column calendar of activities. These activities can include any number of different things to do[2], with activities SB1="don't do anything except the interview" and SB2= "don't wake up at all"[3] as special cases. Each waking activity includes an interview after whatever other things SB gets to do, which is another thing you misrepresented.
So the day+die combinations - ALL M*N OF THEM - each correspond to one cell in this calendar. And one activity which may, or may not, include either of SB1 or SB2. Each combination has the same probability of occurring during the experiment.
And the calendar represents the prior sample space of an experiment where, in SB's "world" during the experiment, one day has been selected from this calendar. This isolation is brought about by not being able to associate today's cell, or the row that contains it, with any other cell. The isolation affects her credence regardless of whether it is due to amnesia or sleep.[4]
So the day+die combination SB is experiencing corresponds to one, and only one, outcome in this calendar/sample space. There are M*N possible selections. Each cell had the same prior probability of having been selected for today's activity, but SB has well-defined "new information" about which it is. That is, her observation of this activity[5] corresponds to how that term is used in probability theory. It does not mean "something happened that was not guaranteed." It divides the prior sample space - the calendar - into those outcomes that are consistent with an observation, and those that are not. The updated probability for row m is the number of times the activity appears in row m, divided by the number of times it occurs in the calendar/sample space. This is what I have said repeatedly, said quite clearly, and what you seem to be avoiding through misrepresentation.
And here is the important part: This calculation cannot be different if an activity that was ruled out by the new information is a waking activity, or what I called SB2. Both represent cells in the calendar that could have been selected for today, but observation says they were not. Cells do not get eliminated from the calendar due to activity SB2, they are simply inconsistent with observation.
This is where you lose me, and diverge from a proper analogy. Why 2^101? Why multiple times after the die roll that corresponds to Heads? Or did you change the question to mean Tails?This is even more obvious when we replace the coin with a 2^100-sided die. If it lands on a 1 then she is woken 2^101 times, otherwise she is woken once. After being woken up she is asked her credence that the die landed on a 1. The experiment is not repeated. — Michael
And this is where you don't seem to understand the classic answers. Halfers will say the answer is 1/2 as long as she is guaranteed to wake at least once. So I don't need to understand your version. Thirders would say either a very large number, or a very small number, depending what I didn't understand; but I see no reason for a "3" to be here.Halfers say that her credence is (1/2)^100 and Thirders say that her credence is 2/3. I think any reasonable person would agree with the Halfer.
+++++
[1] Days and/or columns are independent of the die, or the activities scheduled.
[2] I've chosen to have M activities in the past, just to use fewer different numbers. All that is necessary is at least two.
[3] This still counts as one of my activities, and occupies a cell int he calendar.
[4] That last part is what you keep misrepresenting. Michael too.
[5] Yes, this includes being interviewed without other things happening. -
 Michael
16.6kWhy are you saying the values are wrong? Since there are one and a half awakenings on average per run, it's to be expected that the EV of a single bet placed on any given awakening be exactly two thirds of the EV of a bets placed on any given run. — Pierre-Normand
Michael
16.6kWhy are you saying the values are wrong? Since there are one and a half awakenings on average per run, it's to be expected that the EV of a single bet placed on any given awakening be exactly two thirds of the EV of a bets placed on any given run. — Pierre-Normand
It's wrong because the expected returns aren't £33.333... if betting on heads or £66.666... if betting on tails.
I am not conflating the two. I am rather calculating the EV in the standard way by calculating the weighed sum of the payouts, where the payout of each potential occurrence is weighted by its respective probability (i.e. my credence in that occurrence being actual). I am pointing out that both the Halfer interpretation of SB's credence (that tracks payouts/awakenings) and the Thirder interpretation (that tracks payouts/runs) of SB's credence yield the exact same EV/run (and they also yield the same EV/awakening) and hence Halfer and Thirders must agree on rational betting strategies despite favoring different definitions of what constitutes SB's "credence". — Pierre-Normand
So then can you set out your calculations? These are mine:
I assume yours will take this form?
It just seems to me that you're putting the cart before the horse and arguing that because E(T) = 2 × E(H) then C(T) = which is a nonsensical inference.
And, once again, I think that this inference is shown most evidently to be nonsensical when we consider the case with the 2100-sided die. It just doesn't matter what the payout structure is or whether I'm asked my credence that the die rolled a 1, my credence that this is a die-rolled-a-1 run, or my credence that this is a die-rolled-a-1 awakening: my answer is always going to be , and I think any rational person would answer the same. -
 Michael
16.6k
Michael
16.6k
These were your exact words:
Her credence when asked is 1/3, because of the four possible cells in the 2x2 array, one is eliminated and only one of the remaining three is Heads. — JeffJo
This can be generalised as:
Her credence when asked is , because of the possible cells in the array, are eliminated and only of the remaining has Outcome X.
In the traditional problem the rules are:
- A coin is tossed
- If the coin lands on tails then Sleeping Beauty is woken on Day 1 and Day 2
- If the coin lands on heads then Sleeping Beauty is woken on Day 1
Given this, and where Outcome X is the coin landing on tails, the values are:
Your reasoning entails that Sleeping Beauty's credence that the coin landed on tails is .
In a slightly different version of the problem the rules are:
- A 6-sided die is rolled
- If the die rolls a 1 then Sleeping Beauty is woken on Day 1, Day 2, ... and Day 10
- If the die rolls a 2 then Sleeping Beauty is woken on Day 1
- If the die rolls a 3 then Sleeping Beauty is woken on Day 1
- If the die rolls a 4 then Sleeping Beauty is woken on Day 1
- If the die rolls a 5 then Sleeping Beauty is woken on Day 1
- If the die rolls a 6 then Sleeping Beauty is woken on Day 1
Given this, and where Outcome X is the die rolling a 1, the values are:
Given that , your reasoning entails that Sleeping Beauty's credence that the die rolled a 1 is .
In my extreme version of the problem the rules are:
- A 2100-sided die is rolled
- If the die rolls a 1 then Sleeping Beauty is woken on Day 1, Day 2, ... and Day 2101
- If the die rolls a 2 then Sleeping Beauty is woken on Day 1
- If the die rolls a 3 then Sleeping Beauty is woken on Day 1
...
- If the die rolls a 2100 then Sleeping Beauty is woken on Day 1
Given this, and where Outcome X is the die rolling a 1, the values are:
Given that , your reasoning entails that Sleeping Beauty's credence that the die rolled a 1 is approximately .
Whereas Halfers will say the only thing that Sleeping Beauty needs to consider is the coin toss/die roll, and so her credence in each of these situations is:
- The coin landed on tails:
- The 6-sided die rolled a 1:
- The 2100-sided die rolled a 1: -
 JeffJo
175Given that 10/15=2/3, your reasoning entails that Sleeping Beauty's credence that the die rolled a 1 is 2/3. — Michael
JeffJo
175Given that 10/15=2/3, your reasoning entails that Sleeping Beauty's credence that the die rolled a 1 is 2/3. — Michael
And if it had been a 6-day experiment, it would be 6/10=3/5. The point being that you are constructing a specific case, unclearly (your original didn't say the number of days increased), in order to get that answer. And then presenting the 2/3 answer as a general case, when it is not. And btw, I try to use upper-case letters as the size of the set, and lower case as member of the set. And avoid adding extra symbols when a simple expression or description will suffice.
But to re-center: IN GENERAL, with an MxN calendar - that is, using an M-sided die for an N-day experiment - and some number K of possible activities populating these N*M, which of these is a true statement when activity k is observed:
- The probability of die roll m - that is, row m - is the number of times that activity k appears in row m, divided by the number of times activity k appears in the calendar, regardless of what those activities are.
- The probability of die roll m depends on whether one of the un-observed activities included in the MxN calendar is what I called "SB2," or "don't wake SB up."
This is simple question, that does not require numbers specifically-selected to get specific answers. But I would like to see what you think the dependence on the number of times SB2 appears is, if you think there is one. This is part of what I originally asked for, and it has been quite obviously avoided.
If you want the response to any of your hyperbolic scenarios, you can get it from statement #1 with fewer numbers than you used. -
 Michael
16.6kAnd then presenting the 2/3 answer as a general case — JeffJo
Michael
16.6kAnd then presenting the 2/3 answer as a general case — JeffJo
I'm not.
I'm saying that if this is our experiment:
1. We roll a 2100-sided die
2. Sleeping Beauty is woken up over 2101 days if it rolls a 1
3. Sleeping Beauty is woken up just once if it doesn't roll a 1
Then your reasoning entails that Sleeping Beauty's credence that the die rolled a 1 is , because that's how the waking-day ratio works out.
And I think this is a reductio ad absurdum against your reasoning. A rational person's credence should just be . Therefore, it is wrong to consider the waking-day ratio. -
 JeffJo
175
JeffJo
175
It sure looks like you are. You are selecting numbers to get 2/3 as an answer, when it is not the answer in general. What I keep trying to get across, is that the general case has to work as well.I'm not. — Michael
I'll edit it to make it clearer, and general. Tell me if I got it wrong. (And btw, you can use the list function with "list=1" to get more quotable lists.)I'm saying that if this is our experiment:
- We roll a M-sided die
- Sleeping Beauty is woken on each of N days if it rolls a 1.
- Sleeping Beauty is woken on one randomly-selected day if it doesn't roll a 1
So Activity SB1 appears N times in row 1, and only one time in any other row, for a total of N+M-1.
Her credence in "1" as the die-roll result is N/(N+M-1).
Her credence in any other specific result is 1/(N+M-1).
Her credence in the set of all other results is 1/(N+M-1).
In the classic problem, N=M=2 but you are asking about the probability of tails. N/(N+M-1) = 2/(2+2-1) = 2/3. If we go to 6x6, as in my first post along these lines, it is 6/(6+6-1)=6/11.
If we ask about a specific die roll that isn't 1, as in the classic problem, we get 1/3 and 1/11. That is the typo I thought existed.
Not the ratios I described. Or near the answer if we ask a question as in the classic problem. It is what seems to be a deliberate (otherwise, why change the question, or keep insisting on such specific numbers?) misinterpretation to get this result.Then your reasoning entails that Sleeping Beauty's credence that the die rolled a 1 is 2/3, because that's how the waking-day ratio works out.
You want M=2^100 and N=2^101.
(2^101) / (2^100 + 2^101 - 1) = 2/(3 - 2^(-100))
And I think it is just that against yours. WHICH IS WHY I KEEP ASKING SPECIFIC QUESTIONS, AND GET FRUSTRATED WHEN YOU IGNORE THEM IN FAVOR OF MISREPRESENTATION.And I think this is a reductio ad absurdum against your reasoning.
Play football, tennis, or any other waking activity on the days Sleeping Beauty stays asleep in your problem. Do you think the answer is the same 1/2? Or nearly 2/3? What is the probability of a 2 when she has a different waking activity? Does it depend on how many different ones there are? -
 Michael
16.6k
Michael
16.6k
It is a fact that if this is our experiment
1. We roll a 2100-sided die
2. Sleeping Beauty is woken up over 2101 days if it rolls a 1
3. Sleeping Beauty is woken up just once if it doesn't roll a 1
Then your reasoning entails that Sleeping Beauty's credence that the die rolled a 1 is .
Therefore, your options are:
1. Commit to the conclusion that her credence is
2. Accept that her credence isn't and so that your reasoning is fallacious
3. Arbitrarily decide that your reasoning only works for an grid of a sufficiently small size
So which is it?
I think that any rational person will go with (2). -
 Pierre-Normand
2.9kIt just seems to me that you're putting the cart before the horse and arguing that because E(T) = 2 × E(H) then C(T) = 2/3 — Michael
Pierre-Normand
2.9kIt just seems to me that you're putting the cart before the horse and arguing that because E(T) = 2 × E(H) then C(T) = 2/3 — Michael
I don't do this since, just like you, I take SB's expected value to be a function of both her credence and of the payout structure. I, however, don't take her credence to be a well defined value in the original Sleeping Beauty problem due to an inherent ambiguity in resolving what kind of "event" is implicitly being made reference to in defining her "current epistemic situation" whenever she awakens. In more usual credence calculation problems, there always is a one-to-one mapping between the distinguishable epistemic situations agents finds themselves in in relation to a target outcome and the information available to them in those situations, and so no ambiguity arises. (For instance, when deciding to place a bet while playing poker, there never is an issue of, unbeknownst to me, my having other opportunities to place the same bet before the dealer deals the next card.) In the SB problem, on the other hand, it is unclear whether the two awakening events that take place on the occasion when the coin land Tails merely are two opportunities for the agent to experience and assess a single event (the experimental run) that was actualized, as the Halfer insists, or if instead such an experimental run just is an arbitrary grouping of two separate occasions to experience and assess the coin outcome, as the Thirder insists.
For some reason, both the Thirders and Halfers seem to implicitly assume that there is a fundamental objective truth about the universe that either makes awakening episodes arbitrary ways to carve up objectively defined awakening runs (Halfers) or make experimental runs arbitrary groupings of objectively defined awakening episodes (Thirders). Halfers and Thirders are both right to believe that the the other choice is arbitrary, but they fail to see that, just like their own definitional choice, it constitutes a reasonable interpretation of SB's credence in light of specific pragmatic considerations: What is the point of individually tracking awakening episodes, or runs? Specific payout structures furnish such pragmatic considerations. They don't define "the truth" regarding what it is that objectively defines SB's "credence". Once a determinate way to carve events in SB's "experience" and thereby fully define the topometry of the relevant sample space, the expected values of all the possible betting strategies become well defined and both Halfers and Thirders agree on them in spite of their varying definitions of SB's credence. -
 JeffJo
175
JeffJo
175
It is a lie that that is my argument. I'm sorry to be so blunt, but I have repeated my argument for you, and this is not it. If you do not understand why I say this, you can ask for clarification as to why the denominator is wrong. But I did show you.It is a fact that if this is our experiment
1. We roll a 2^100-sided die
2. Sleeping Beauty is woken up over 2^101 days if it rolls a 1
3. Sleeping Beauty is woken up just once if it doesn't roll a 1
Then your reasoning entails that Sleeping Beauty's credence that the die rolled a 1 is 2/3. — Michael
My options seem to be to keep repeating what I've said, or somehow get you to explain what you think is "my reasoning" that leads to this result. But since I described it many times, and get a different result, I'm not hopeful.Therefore, your options are: -
 Michael
16.6k
Michael
16.6k
These are your exact words:
Her credence in "1" as the die-roll result is N/(N+M-1). — JeffJo
If this is our experiment:
1. We roll a 2100-sided die
2. Sleeping Beauty is woken up over 2101 days if it rolls a 1
3. Sleeping Beauty is woken up just once if it doesn't roll a 1
Then and .
Therefore, according to your reasoning, her credence is which . You can see here if you don't believe me.
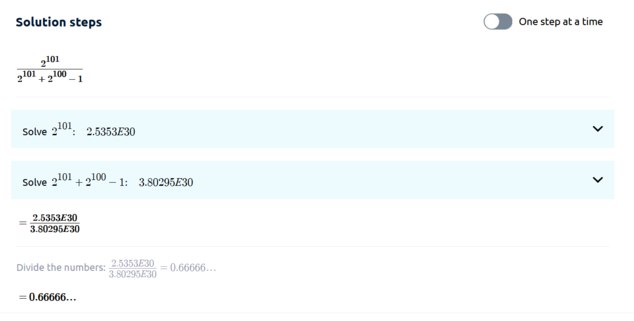
-
 JeffJo
175Therefore, according to your reasoning, her credence is 21012101+2100−1 which ≈23. You can see here if you don't believe me. — Michael
JeffJo
175Therefore, according to your reasoning, her credence is 21012101+2100−1 which ≈23. You can see here if you don't believe me. — Michael
Yes, it sure is close. But not exact. Maybe you could explain why we can approximate, and why only this one example chosen to produce that result is important?
Or, you could address the general case, which gets lots of different answers. Or address what happens if she is woken all of the days but sometimes does something else. -
 Michael
16.6kYes, it sure is close. But not exact. — JeffJo
Michael
16.6kYes, it sure is close. But not exact. — JeffJo
So you're willing to commit to the conclusion that Sleeping Beauty's credence that the 2100-sided die rolled a 1 is , i.e. she should be fairly confident that the die rolled a 1?
Because I take that as a reductio ad absurdum. If Sleeping Beauty is rational then her credence should be , i.e. she should be almost certain that the die didn't roll a 1.
The waking-day ratio is a red herring.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum




