-
 Michael
16.8kIf you are not willing to justify your model empirically, well then that says it all. You should be willing to empirically justify your theory. — Jeremiah
Michael
16.8kIf you are not willing to justify your model empirically, well then that says it all. You should be willing to empirically justify your theory. — Jeremiah
I am. I already ran the simulation.
I've also built the game for us to play here.
First select your chosen envelope. Then select either "switch" or "stick". Then press "next" to play the next game.
Using my strategy for 50 games gave this result:
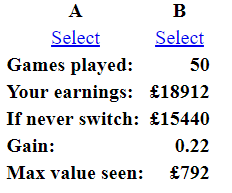
-
 Jeremiah
1.5k
Jeremiah
1.5k
You still need to notate your code. Especially on forums like these. I don't know why you don't do that. It almost makes it seem like you are trying to hide your assumptions in the code.
You are still using your incorrect sample space.
I am not going to look at any more code that is not notated. I mean that should just be common sense if you are going to post it here. -
 Michael
16.8kHere you ran your own simulation with X selected at random (multiples of 10).
Michael
16.8kHere you ran your own simulation with X selected at random (multiples of 10).
You then ran the simulation with other methods of selecting X and said "the distribution in which X was selected from is not significant when assessing the possible outcome of envelope A and B concerning X or 2X".
I'll try running my simulation using the three other methods you described and see if I get the same .25 gain (or a gain of any amount). -
 Michael
16.8kIf you are doing it based on the your X, X/2 sample space, you'll get your expected gain. — Jeremiah
Michael
16.8kIf you are doing it based on the your X, X/2 sample space, you'll get your expected gain. — Jeremiah
There's nothing like that. I just open my envelope, which contains either X or 2X, and I switch if it's less than or equal to the highest X I've seen.
Perhaps you could point out which line(s) of my code you disagree with. Is it just how I select X?
x <- sample(1:100, 1) * 4
-
 Jeremiah
1.5k
Jeremiah
1.5k
No, I used the same scale in my code.
It is this:
if ( 0 == max_2x || choice <= max_2x / 2 ) { switch <- switch + other } # Otherwise increase the switching strategy amount by the amount in the chosen # envelope else { switch <- switch + choice } # Record the highest value seen max_2x <- max(c(choice, other, max_2x))
You code is based off your assumptions. -
 Michael
16.8kYou code is based off your assumptions. — Jeremiah
Michael
16.8kYou code is based off your assumptions. — Jeremiah
Huh? That's not an assumption. That's my strategy. I switch envelopes if the value in my envelope is less than or equal to the highest X I've seen in previous games.
So if in the first game we have £10 and £20 then in the second game I switch if I have £10 but not if I have £20. -
 Michael
16.8k
Michael
16.8k
So first you say "If you are not willing to justify your model empirically, well then that says it all. You should be willing to empirically justify your theory." and then you don't like when I test my theory by playing 100 games? That makes no sense.
Even if you don't like that I get to remember previous games, there can still be a gain if we choose some arbitrary amount to be the limit for when I decide to switch. So, if I were to always switch if my envelope contains £400 or less and stick otherwise then using my simulation I would gain .25. If my limit was £200 then I would gain 0.0625. If my limit was £600 then I would gain ~0.145.
The formula for the expected gain, as explained here, is where is the highest that can be selected by the host and is our chosen limit for switching (although as I also say there, this formula only works when our limit is less than or equal to ; I haven't worked out the formula for when it's greater).
So re-run my simulation but replace the lines you don't like with:
# If the amount in the chosen envelope is less than or equal to # 300 then switch and increase the switching strategy amount # by the amount in the new envelope if (choice <= 300) { switch <- switch + other } # Otherwise increase the switching strategy amount by the amount in the chosen # envelope else { switch <- switch + choice }
The gain is ~0.14. -
 Jeremiah
1.5k
Jeremiah
1.5k
I already ran my own simulations, Michael, and the idea that if this was a game you'd get many turns to learn the range is very unrealistic. This is what I am not interested in. I didn't get into statistics to map people subjective assumptions. I can do that without math. -
 Michael
16.8kAs I said above, you don't need to learn the range. You can choose any arbitrary amount before you start and switch only if the amount in your envelope is less than or equal to that amount. You will have an expected gain if your chosen amount is less than the highest 2X envelope, with a best case scenario of .25 if your chosen amount happens to be the highest X envelope.
Michael
16.8kAs I said above, you don't need to learn the range. You can choose any arbitrary amount before you start and switch only if the amount in your envelope is less than or equal to that amount. You will have an expected gain if your chosen amount is less than the highest 2X envelope, with a best case scenario of .25 if your chosen amount happens to be the highest X envelope. -
 Srap Tasmaner
5.2k
Srap Tasmaner
5.2k
There are Sometimes Switch strategies that work, so far as I can tell.
Do you believe that shows that your original argument, which concludes that the value of whatever envelope you don't have is 1/4 more than the one you do have, is valid? -
 Michael
16.8kDo you believe that shows that your original argument, which concludes that the value of whatever envelope you don't have is 1/4 more than the one you do have, is valid? — Srap Tasmaner
Michael
16.8kDo you believe that shows that your original argument, which concludes that the value of whatever envelope you don't have is 1/4 more than the one you do have, is valid? — Srap Tasmaner
The expected value (given the information available to us), yes. -
 Srap Tasmaner
5.2k
Srap Tasmaner
5.2k
But that argument, that "calculation", is not based on using any particular strategy. It's just this:
E(U)=.5(2Y) + .5(Y/2)
Do you believe that the success of the various switching strategies available shows that this expectation is correct? -
 Michael
16.8kYes, which is why my switching strategy (and the second switching strategy in the paper you referred to) provides a gain of .25. It's not a coincidence that the values coincide.
Michael
16.8kYes, which is why my switching strategy (and the second switching strategy in the paper you referred to) provides a gain of .25. It's not a coincidence that the values coincide. -
 Srap Tasmaner
5.2k
Srap Tasmaner
5.2k
If that expected value calculation is correct, then Always Switch should produce the expected gain, shouldn't it?
What, in that formula, suggests that a Sometimes Switch strategy is correct? -
 Michael
16.8kIf that expected value calculation is correct, then Always Switch should produce the expected gain, shouldn't it? — Srap Tasmaner
Michael
16.8kIf that expected value calculation is correct, then Always Switch should produce the expected gain, shouldn't it? — Srap Tasmaner
No, because if the amount in your envelope (say £160) is more than the highest X that the host can choose (say £100) then you're always going to lose, even though the expected value of the other envelope, given the information available to you, is £200.
This is the fact that my strategy accounts for.
What, in that formula, suggests that a Sometimes Switch strategy is correct? — Srap Tasmaner
I don't know what you mean by this. The simulation of the strategy shows that the strategy is correct. The formula just explains why the gain from the strategy is 0.25; the expected value of the other envelope is .
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum



