-
 Banno
30.3k
Banno
30.3k -
 bongo fury
1.8kWorth a look. — Banno
bongo fury
1.8kWorth a look. — Banno
No doubt. At all.
"Discover" seemed weird though...
One can discover a truth without being the first to discover it (in this context); it is enough that one comes to believe it in an independent, reliable and rational way.
In that case, why not "understand"? Perhaps because he associates that with "prove"?
The difference between merely discovering a truth and proving it is a matter of transparency: for proving or following a proof the subject must be aware of the way in which the conclusion is reached and the soundness of that way; this is not required for discovery.
Ok, but then what has happened to "in an independent, reliable and rational way"?
Also, somewhat of a wtf at this,
While there is no reason to think that mental arithmetic (mental calculation in the integers and rational numbers) typically involves much visual thinking,
... said reaction not much assuaged even by a chapter in here entitled Mental Number Lines, which (dashing my hopes) rather suggests that the (same) author is among those who, incomprehensibly to the rest of us,
form a number line representation [only] once we have acquired a written numeral system.
Perhaps it is largely in this group of people that we find those benighted politicians and educators who would (unlike probably the author, to be fair) invite children to approach mental arithmetic as an abacus or column digit system? Instead of (what seems more natural and profitable to the rest of us) as a matter of travelling between locations on a line?
I wonder in what kind of ratio the two kinds of people size up... 50 50? -
 jgill
4kThat article does go on and on. I burned out after a short spell. Fifty years ago I was formulating my dissertation and was stuck at a difficult point involving a kind of infinite iteration. As I was lying in bed one night, beginning to drift off, I suddenly envisioned a geometrical image that provided a key to completing both the structure and proof of a difficult theorem. I still do a bit of research and imagery is important, although it's rare that a proof itself relies on geometrical figures.
jgill
4kThat article does go on and on. I burned out after a short spell. Fifty years ago I was formulating my dissertation and was stuck at a difficult point involving a kind of infinite iteration. As I was lying in bed one night, beginning to drift off, I suddenly envisioned a geometrical image that provided a key to completing both the structure and proof of a difficult theorem. I still do a bit of research and imagery is important, although it's rare that a proof itself relies on geometrical figures.
At one time it was required that a student take a course in analytic geometry prior to an introduction to calculus. All the imagery in that course provided a bridge of understanding for calculus. Nowadays, that material is squeezed into calculus, and there are even calculus curricula that attempt to minimize imagery by going into n-dimensional vector spaces immediately. -
 alcontali
1.3kThe Epistemology of Visual Thinking in Mathematics — Banno
alcontali
1.3kThe Epistemology of Visual Thinking in Mathematics — Banno
It's a really long article ...
Visual thinking is undoubtedly a staple in those areas in mathematics, such as geometry, that end up downstream in construction engineering, mechanical engineering, select areas in science, and so on.
There are entire areas in mathematics, however, where visual thinking would probably only add to the confusion, certainly in computer-science related areas of pure mathematics, where symbol manipulation alone is much more common.
When recently looking into the bi-interpretability of ZF-∞ and PA, I ran into the concept of arithmetic sets.
For example: { 1, 3, 7 } can be written arithmetically { x | x=1 or x=3 or x=7 }, and can therefore be represented by the predicate φ(x) := x=1 or x=3 or x=7.
I do not see how visual thinking with diagrams or images would be helpful in clarifying this concept?
As far as I am concerned, the only thing that really helps, are good examples, which are almost always lacking. Just look at the Wikipedia page itself: no examples at all. That is why I am still struggling a bit with for example:
{ 1, 8, { 45, 6 }, 9 } could arithmetically be: { x | x=1 or x=8 or x= { y | y=45 or y=6 } or x=9 }
It may be the correct arithmetic translation of this example of an embedded set expression, but I am not sure, because it could also be wrong. I would only be able to confirm when seeing a similar example elsewhere, but that example is not forthcoming; certainly not by Google searching for it. Instead of showing good examples, they will probably rather come up with a useless diagram or image or so ... ha ah aha! ;-) -
 jgill
4kAs far as I am concerned, the only thing that really helps, are good examples, which are almost always lacking — alcontali
jgill
4kAs far as I am concerned, the only thing that really helps, are good examples, which are almost always lacking — alcontali
Good point. The only trait I share with R. Feynman is the process of learning a difficult concept by looking at examples. There are many mathematicians who can understand abstract notions very quickly simply by the words and symbols describing them. I envy them this ability. By studying examples it all clicks into place for me.
Many years ago I knew of a graduate student who spent a couple of years working up his PhD research project on a class of functions. Then one day he was asked for an example. A fruitless endeavor, for he soon learned the set of such functions was the empty set. :worry: -
 A Seagull
615The Epistemology of Visual Thinking in Mathematics
A Seagull
615The Epistemology of Visual Thinking in Mathematics
. — Banno
An interesting article. Not sure why it refers to itself as an epistemology.
It highlights the conflation of pure and applied mathematics. (a priori and a posteriori). Children learn maths counting sheep (well I did anyway) which is applied maths, yet maths itself is pure.
It also highlights how possible proofs of theorems are first visualised by mathematicians before they try to construct a rigorous proof.
It also suggests how the possible axioms and rules of inference of maths may be visualised first before they implemented. I am thinking here of when calculus and complex numbers were added to the canon of mathematical axioms and rules of inference. -
 Qwex
366Visual thinking is cruical when understanding words.
Qwex
366Visual thinking is cruical when understanding words.
If the word 'orange' did not prompt the color orange, we would find it much harder to communicate ideas.
If I say 'sandwitch' you visualize it.
If you listen to a song, you visualize an image to help comfort and expand your thoughts. I guess, there's a visual layer to thought.
Hold a visualization for a few seconds and scan the degrade effect - the sandwitch is scaled - we use our mental agility to scale it.
I'd say during the degrade, partial rotation is simulated. There's some element of an id scan.
Try now that comfort image you visualize as per the music example. A non-specific image with a identity. This is scaled in the same manner, as a specific image. -
 Gregory
5kIf I pick of an orange blanket and show it to the learning child and say "orange" and then say orange when picking up an orange toy, the child could think the word "orange" means means "picking something up". There are many mazes to go through without intuition and maybe that that autism is. Imagination with intuition is the best. When people make distinctions between classes, sets, and collections, I wonder which of those two they rely on more. Can there be a a hermaphrodite entity that.is half number and half set?
Gregory
5kIf I pick of an orange blanket and show it to the learning child and say "orange" and then say orange when picking up an orange toy, the child could think the word "orange" means means "picking something up". There are many mazes to go through without intuition and maybe that that autism is. Imagination with intuition is the best. When people make distinctions between classes, sets, and collections, I wonder which of those two they rely on more. Can there be a a hermaphrodite entity that.is half number and half set? -
 bongo fury
1.8kAnd if someone does not see it thus, but sees it so...
bongo fury
1.8kAnd if someone does not see it thus, but sees it so...
...then it's not a justification at all. — Banno
And this couldn't as easily happen with words? That the person doesn't hear/think them thus but hears/thinks them so?
for proving or following a proof the subject must be aware of the way in which the conclusion is reached and the soundness of that way; — Giaquinto
(The quote is from a contrast of proof with discovery, but if I wasn't mistaken this was meant to correlate roughly with that of words with pictures.)
Again, I'm not seeing any important difference between words and pictures. I'm just as likely to follow a textual proof uncomprehendingly or inappropriately as a visual one, am I not?
And an automatic prover would (in principle) be indifferent as regards type of symbols, would it not? -
 Banno
30.3kYou're perhaps looking for an argument whee there isn't one.
Banno
30.3kYou're perhaps looking for an argument whee there isn't one.
I'm more interested here in the distinction between showing and stating. -
 bongo fury
1.8k
bongo fury
1.8k -
 Banno
30.3k:nerd:
Banno
30.3k:nerd:
But I can't quite set out the issue...

Does this say or show? I'm not so sure of the distinction any more.
Isn't understanding a proof a kind of discovery? -
 bongo fury
1.8k
bongo fury
1.8k -
 bongo fury
1.8kDoes this say or show? — Banno
bongo fury
1.8kDoes this say or show? — Banno
It exemplifies the pattern, yes? So, shows an instance. -
 bongo fury
1.8kIt states a sentence, as a conclusion, and it exemplifies ("shows") a pattern of inference. Which is justifying ("showing") the conclusion, but not justifying ("showing") the pattern of inference. (?)
bongo fury
1.8kIt states a sentence, as a conclusion, and it exemplifies ("shows") a pattern of inference. Which is justifying ("showing") the conclusion, but not justifying ("showing") the pattern of inference. (?) -
 Banno
30.3k
Banno
30.3k -
 bongo fury
1.8kDoes it differ significantly from fig 1?
bongo fury
1.8kDoes it differ significantly from fig 1?
I can't see how. — Banno
Me neither, in respect of whether it counts as a 'real' proof. Isn't this a live area? I thought that article was going to update me, but it wasn't quite that area. But I wouldn't be about to try persuading you otherwise.
saying is a complicated way of showing. — Banno
In what way complicated? Is the justifying/demonstrating/showing perhaps more complicated than the exemplifying/showing? -
Templisonanum
2All forms of communication are a visualization. This proof shows symmetry, equivalency, and negation, to lead to a trivial result.
I believe saying something is strictly associated with verbalization, and that written words are as much as showing as diagrams would be. -
 fdrake
7.2kI really enjoyed the discussion about reasoning being schematic or not. Roughly, reasoning to demonstrate a claim schematic when it applies to every instance of a kind, even though it uses an instance to demonstrate it.
fdrake
7.2kI really enjoyed the discussion about reasoning being schematic or not. Roughly, reasoning to demonstrate a claim schematic when it applies to every instance of a kind, even though it uses an instance to demonstrate it.
Schematically put, in reasoning about things of kind K, once we have shown that from certain premisses it follows that such-and-such a condition is true of arbitrary instance c, we can validly infer from those same premisses that that condition is true of all Ks, with the proviso that neither the condition nor any premiss mentions c
Like this proof that 3 is prime. A number is prime if it has no divisors other than itself and 1 (and is not itself 1). The divisors of 3 must be less than it. 1 is not a divisor of 3. 2 is not a divisor of 3. Therefore 3 has no divisors other than itself and 1. The same procedure could be used for any number - exhaustively try to eliminate numbers less than it from the possible list of divisors of it, if you do all the numbers less than it and eliminate every one, the number is prime.
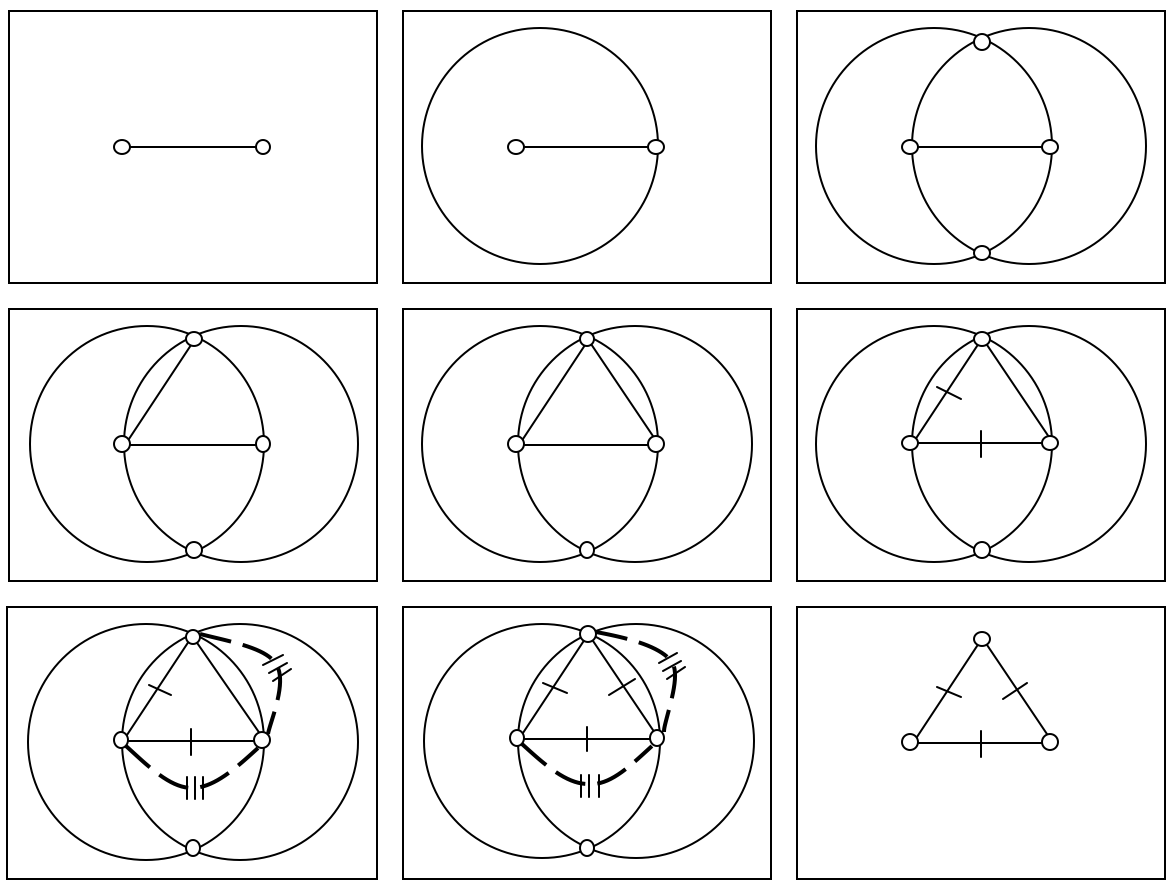
Failure of a proof attempt being schematic is also interesting; like these demonstrations of De Morgan's laws:
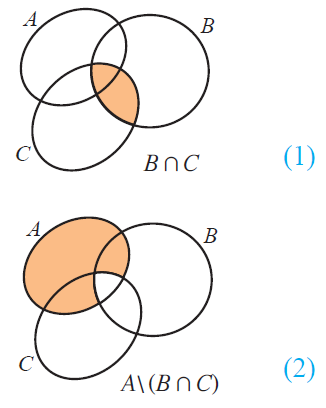
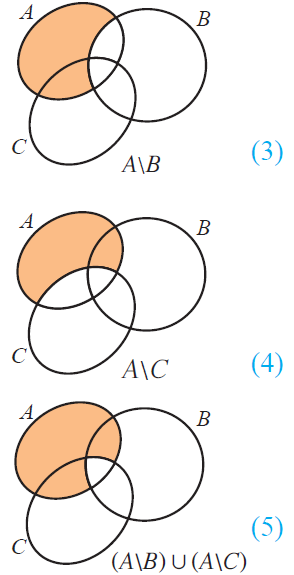
It makes what the theorems mean exceptionally clear, but not all sets can be represented as connected subsets of the plane! So it fails as a proof. (@Banno someone perverse might see the proof as about the bits which are not shaded...)
Something that I'm a bit conflicted about is whether the bolded characterisation is spot on.
The distinction between schematic and non-schematic proof attempts should apply generically; we could make it line up and stipulate that schematic reasoning is necessarily correct, insofar as it is stipulated to apply only to a successful proof that a property holds of a kind through clever use of an example. But it seems to me there are relevant hows and whys; why is a proof attempt schematic or not, what blocks it from being so? Conversely, what distinguishes schematic proofs from non-schematic ones?
What blocks a proof from being schematic might be something incidental in each case; like the sets being connected subsets of the plane. That failure of schematic reasoning would only apply to set logic laws being illustrated in the plane (or other things being demonstrated geometrically). There will be restrictions of scope for the ambit of these incidental failures. But really what these incidental features will do is block an inference in the proof, or restrict its result to a subcase. IE: "you can't make this inference in step 2 to step 3 because blah" or "the proof works but you made an assumption in step 154 that makes it only apply to blah". Those are generic reasons for proof failure, rather than a specific failure related to a proof attempt being schematic.
If we focus in on the second case; when the original proof is made to apply to some kind but actually applies to some subkind, it would fail to be schematic for the original kind, but if it was tweaked to state the assumption explicitly, it would become an example of schematic reasoning for the restricted kind. Even though only one or two steps in the reasoning have changed.
It is just counterintuitive to me that whether some proof is schematic or not can depend upon such a small change; the intended target, when the rest of the characterisation of being schematic also applies to the steps in the proof.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum