Comments
-
Determinism vs. PredictabilityTerms I could use help with - "structures are internalized;" "functionally bounded system;" and "demarcated modes of operation." — T Clark
Thank you for your patience. These are still things I'm wrestling with, and it is very good to have someone who is actually interested in my wrestling with them.
"Structures are internalised" isn't something really statisticsy, I guess I just used it as a placeholder. We might say that electrical flow is an 'internalised structure' of a circuit, so are the wires and conductivity, voltages, currents, their relationships. They don't have much to do with nuclear bombs or sledgehammers or wire cutters even though they can all destroy circuits.
"Functionally bounded system" is another placeholder. Whenever you find some system behaving in some way, it behaves in the ways it does rather than in all ways it could behave. Realising any counterfactual of a system seems to require either further evolution along one of its trajectories; like time increasing in heat dissipation of an object as a function of time making the object go to about the environmental temperature. Or the introduction of a new regime of behaviour relevant to the previously established one; like when enzymes lock with their substrates and go from floating proteins (orientations of proteins and position and their time changes) to part of the molecular factory of digestion (enzymes working to produce nutrients). That "Or" is not an exclusive or.
When you have an infinite intellect, nothing really realises in the first sense (within the same regime) and nothing really novel happens (no new regimes), so we're left with a completely timeless completely described blob.
"demarcated modes of operation" was another placeholder. Imagine you disperse some amylase in solution with some starch molecules. Both the starch and the amylase are jiggling about independently for the most part. If you were to model their positions and velocities and orientations, they'd keep on wiggling along indifferent to each other until... they got close, and one breaks the other apart. The starch and the amylase have demarcated modes of operation; moving about independently; until they get sufficiently close to interact (yielding a new regime of behaviour). Their movements may as well be different dynamical systems until they interact, and these two independent subsystems are demarcated modes of operation within the starch-amylase system. -
Determinism vs. PredictabilityIt's a theoretical projection based on the principle of what an all-knowing mind would know. As Hawkings famously said, 'If we discover a complete theory, it would be the ultimate triumph of human reason – for then we should know the mind of God.' — Wayfarer
Going out on a limb here.
I guess what I'm gesturing towards is why should we care about the perspective of God on a system when God's external to it? It's a question of how structures are internalised to systems, rather than abstracting away from the details of all of them. So in my question to @frank, "who's doing the knowing?", who does the knowing that vouchsafes this kind of determinism? It can't be located within a functionally bounded system - one which has demarcated modes of operation, it can only be the totality of all things viewed from the perspective of that infinite intellect.
Thanks for your explanation. It's still not clear to me why you think,assuming that the physical world is completely deterministic, chance could come into it, other than conceptually in relation to our predictions. — Janus
Well randomness doesn't have to be like the popular notion of it. Random variables are just normalised measurable functions on some sigma-algebra of events. The sigma algebra of events can be (associated with) a deterministic dynamical system, and there will still be random variables induced by the transitions of this dynamical system. Like the Bernoulli distribution emerges out of deterministic coin flipping (probably due to initial condition sensitivity of the flipping dynamics). Randomness is much more like forgetting some parts of a system's structure through suitable aggregation of its events than unstructured exceptions to linear notions of cause. -
My notes on the Definition of Mathematics.
How do you both deal with that people wrestle with axioms as much as theorems? The Hilbert program's legacy (and logicism) is on the one hand to find a unifying logical system for all mathematics (which failed, strictly speaking), but the more pernicious legacy is thinking of mathematical theories as given by their axioms. Which is true in a logical/model theoretic sense, but what's really interesting about axiomatisations is how they allow mathematical structures to flower from them.
For a mathematical analogy; imagine that you have an idea of a structure you want to capture the behaviour of, and you have the behaviour, taking a 'pre-image' of that behaviour (through provability) to the axioms which engender it is just as vital a part of mathematics. If ever you've tried to axiomatise a structure you'd see that there's a reciprocality between the structure's concept and its mathematical definition. -
Determinism vs. PredictabilityAs I've said, there are times when knowing all relevant information isn't possible, even in theory. Even if it were possible, that information would also have to be processed in order to make a prediction. — T Clark
If we flip one coin, we know zero, nada, not-a-fucking-thing about the outcome (unless the system is rigged or we have Laplace's demon on hand.) I'm sure you agree with that? — frank
You actually know quite a lot about the outcome. It's described as 50% heads 50% tails. We don't know what the outcome is but we have a complete specification of the system; all relevant info is encoded there, right? Anyway.
Let's look at determinism as captured in Wayfarer's quote of Laplace.
We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom... — Wayfarer
From which you can distill two principles.
(1) If you have a complete specification of a system at some time t, then it is specified for all times before t and after t. Positions, momenta, orientations, that kind of thing.
(2) The specification procedure for all preceding and following states can be obtained by 'submitting the data to analysis'. Presumably this is a codification of all relationships of the basic variables of nature that entail everything about everything else given sufficient manipulation.
and from the remainder of the quote.
for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.
(3) In such a description, nothing would be uncertain (for the subject of 1 which has the specification procedure in 2).
I wanna say that (1) is purely an ontological claim; it concerns the nature of nature/being/One/All/Many/process/stuff/whatever. (2) is talking about a codification of the information in (1), if it can all be distilled into some placeholder. It is how the 'complete' specification' in (1) would be articulated. Then we have that if (1) is true and (2) exists, nothing would be uncertain for that intellect.
So there's a lot going on there. (1) and (2) together still look like determinism, and don't have any epistemic valences. But (3) uses 'uncertain' in a colloquial sense, as in 'there is nothing which could not be known/predicated/anticipated' by the intellect.
We know that (1) is false, so long as we take a realist interpretation of the wavefunction in quantum mechanics. It might fail for other reasons too, but this suffices. There's randomness in nature.
Interestingly (2) also seems to be false, at least if we make the assumption that the grand complete specification in Laplace's formulation is the result of an algorithm, anyway. And not some divine act of comprehension.
I know this doesn't really clear up much of the relationship between uncertainty and determinism, or randomness and determinism, but hopefully it provides a useful distinction between what's going on in (1), (2) and (3). -
Determinism vs. PredictabilityThis is way of presenting logical possibility. True, it's derived from facts about the system, but it's still at most a way of weighing expectation. It's an expression of uncertainty. We actually have no knowledge about which side will land face-up unless the system is rigged. — frank
And yet the real instances of flipping fair coins produce this kind of distribution. Very similar to sex proportions in birth. The claim that 'if we knew all relevant information then the future would be fixed' isn't inconsistent with probability; when what flipping a coin is contains that uncertainty about the future.
Who is doing all this knowing? Where is it in the system? -
Determinism vs. PredictabilityWould you say probability is a "latent structure" of the deterministic system itself or merely of our attempt to understand it? — Janus
It can be either or both. I'll focus on it as a latent structure, seeing as the epistemic angle is well known.
The distribution of outcomes H-T-H-... or whatever derives from the dynamics of coin flipping but is a legitimate part of the system as much as the centre of mass/centroid being in the same place on the coin. Another example there is if you throw a football around (which is very spherical) the probability that it comes to rest on any given side should be approximately equal to the proportion that side is of the surface area. I think this notion is summarised by all points on the faces of the coin and the faces of the football being generic, so that when you partition the surface into the faces (heads/tails, each football face) the uniform distribution holds of the partition.
A more realistic system might be a melting candle in a restaurant near a door. The candle's lit, the wind's blowing through the door. The gusts are of random strength and direction, but they tend to come in through the door. The candle will melt more on the side furthest away from the wind's gusts since they will bend the flame that way. An adequate description of that system would be some model of how the candle melts in the absence of wind plus some directional wind that changes the proximity of the flame to one side of the candle. If you could find the effect of a gust on the rate of change of the candle wax melting in that direction, then make the gusts random (but clustered in appropriate directions and of appropriate strengths), that would be an adequate description of the system.
AFAIK that can actually be done with bridges, stress testing can be done in mathematical models by looking at them in a random form, adding random forces and torsions. Seeing how the bridge would respond to them. -
Determinism vs. PredictabilityJust want to throw this into the hat.
You flip a fair coin, the probability of heads is 0.5, the probability of tails is 0.5. The outcome is not predictable, but the probabilistic behaviour can be fully specified. Whether this behaviour arises from true randomness or as a result of an intricate dependence of the dynamics of coin flipping to the forces applied to lend it rotation and project it through the air, the distribution of heads and tails is still part of the system. Probability's a latent structure of even fully deterministic systems. -
Feature requests
I quite like it. It's much easier to have a pre-filter to inform mod action than to have us scanning the boards for the worst drivel all the time. It catches the bottom of the barrel and real spam and bots. -
Alternatives to 'new atheism'I think the best 'defense' against mysticism is twofold. The first is an understanding of the patterns of reason and emotion that lead to it, the second is a cultivated indifference to any questions formulated in those terms. To reject god, reject theological thinking.
-
Volcanic Soils (rants on systems ontology)So a cool trick with thinking is the interplay between procedural descriptions and diagrammatic representations of them.
Condensing a decision process into a flow chart lets you think about the tasks involved in each arrow.
Writing down required inputs and outputs for an algorithm helps you code it.
The same is true for mathematical ideas. But a relatively unique (I think) thing about such diagrammatic representations of processes in math is that you can ask mathematical questions about the diagram to analyse the original idea. Leonhard Susskind invented the idea of the "world-sheet" in string theory by drawing two Feynmann diagrams up on a board at right angles to each other, then started analysing what it would even mean to rotate them like that and treat them as sides of a shape.
The same seems to be true when wrestling with the mathematisation of ideas, and using math to study ideas and lend them precision. So I drew a diagram of some of the ideas I've been ranting about.
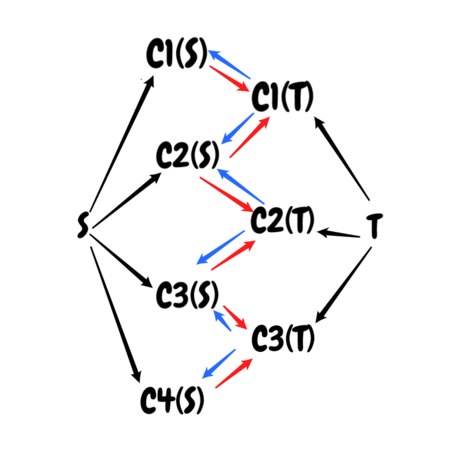
Two systems and have some parameters associated with them and . The black arrows take the underlying systems to the salient features of their dynamics. Then the red and blue arrows link the parameters through functional relationships. The actual structure of the relationships there is arbitrary, it's just supposed to be a reasonably general picture of what's going on.
For a specific (overly simple) system, we can look at the Lotka-Volterra equations in predator-prey dynamics:
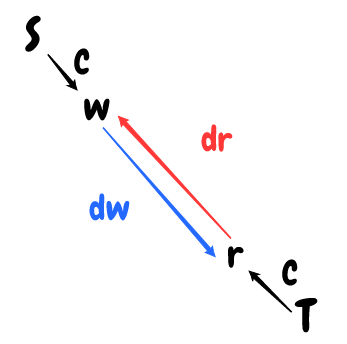
The system is the behaviour of the wolves, the system is the behaviour of the rabbits. These map to the number of wolves and the number of rabbits through (the black arrows).
Then we have the relationships of these parameters, how to get from to on the graph. The blue arrow and the red arrow correspond to the equations:
An insight that can be gained from this portrayal is the distinction between two problems; the parameter emergence problem and the parameter interaction problem. The black arrows take systems and coalesce them into parameters; parameter emergence. The red and blue arrows take coalescences of parameters and describe the effect of one system on another through their functional dependence; the parameter interaction problem.
Parameter emergence in a system is the question of how a system congeals into distinct flows with characteristic features, parameter interaction is the question of how the characteristic features of complex systems interact with each other.
Specific instances of parameter interaction are the usual domain of mathematical models and natural laws, , . Rarely do we consider how complex systems obtain the directions of variation that allow their sub-systems to couple. -
The Population Bomb Did Not DisappearEnvironmental constraints/carrying capacity are much more about the population growth of consumers and our industrial support than the raw population numbers. A few more million poor Indians won't matter as much as a few more million Humvee drivers.
-
Pronouns and GenderThat's kind of in line with me not caring for conventions of etiquette in general. If you're going to have a problem with me not using the "right" silverware, not eating in the "right" order, not following some arbitrary set of ritualistic behavior, etc., then you'd probably better not hang out with me. You can do whatever you want and I won't give you a hard time about it. But I'm going to do the same thing, and I expect you to not give me a hard time about it, too. — Terrapin Station
If you don't care about etiquette in general this is a deeper problem than just apparently bollocks pronouns, sis. -
Pronouns and GenderI just don't understand the need to care so much about this. Why are so many people pedants when it comes to inventing pronouns when:
"humba wumba shlumba dumbha, these sounds even in the haze"
"Twas brillig and the slithy toves..."
"embiggen"
are fine. Do people see no difference between sex and gender? As it applies arbitrarily; at one point does a river in France stop having a penis and become a giant vagina? Well no of course it only applies to bodies. But that's sex, right? Gender's a social construct linked to sexed and sexualised bodies.
But then there's intersex people, demipenises and stuff (I could eat a whole box of those). And chromosomes? Intersex can change that too.
If someone wants to be a fucking genderqueer blue wolf who uses "zem" pronouns why the hell do you care. -
Is the Best Strategy for A.I. Cooperation?General AIs have to deal with the framing problem
“How … does the machine's program determine which beliefs the robot ought to re-evaluate given that it has embarked upon some or other course of action?” — Fodor
Machine learning algorithms, despite all being able to be applied to a wide class of problems, still have to have data and a notion of correctness by which its outputs are judged (a loss function). They also still need to have a specified architecture of parameters (like nodes in a neural net) and their relationships (connections and update rules). These parameters store only one thing. Once the algorithm has been trained, it can make predictions or update itself from new input data for the same task but not for different tasks. Google's AlphaZero chess engine has no strategy lessons for Google's Alpha-Go go engine. But bartenders and waiters have things to learn from each other and points of difference.
General AIs would be generalising intelligences, not just masters of many tasks. They need to learn what tasks are as well as to perform them well, they need to learn criteria to judge themselves on rather than have those criteria as structural constraints. This is a fungibility of form and function present in human learning but not in our best algorithms.
So with respect to the OP, cooperation isn't just one thing, it's task specific and there are generalities which don't necessarily have overlap (eg, dove/hawk is violence based in a state of complete information, prisoner's dilemma is nonviolent based in a state of incomplete information; initiative plays a role in Go and Chess but what advantages it offers in each differ). Cooperation as a strategy in the prisoner's dilemma is different from doves/hawks in the evolutionary game theory. Different again between real people collaborating on something; a good friend is not necessarily a good co-worker at your job.
You're thinking extremely broadly and speculatively without much research on the topic. -
Philosophy of software engineering?That wiki page is about workflow design and programming language styles in programming. Not anything about philosophy; it's philosophy in the sense of perspective rather than the topic of this site. You're looking for this kind of thing.
-
RIP Bryan MageeSad to hear this. The show he did with Ayer on Russel and Frege was one of the things that made me want to start studying philosophy.
-
"White privilege"If the claim isn't falsifiable, there's no way to say that it's not merely a matter of the narrative that folks want to create, and nothing could possibly sway them from that narrative, even if it has no relation to reality. — Terrapin Station
Unfasifiable => narratively driven.
Test that. -
MetaphysicsOn a graph of urgency against feasibility, where do you plot the bard's question (or that of the nature of the world beyond the physics), relative to broken leg diagnosis and war trials conduct? — bongo fury
Having been unable to quantify the urgency of concepts or the feasibility of their implementation in the general case, I have no idea.
| .
|___
There. -
Morality is about rejection of the world“All right," said Susan. "I'm not stupid. You're saying humans need... fantasies to make life bearable."
REALLY? AS IF IT WAS SOME KIND OF PINK PILL? NO. HUMANS NEED FANTASY TO BE HUMAN. TO BE THE PLACE WHERE THE FALLING ANGEL MEETS THE RISING APE.
"Tooth fairies? Hogfathers? Little—"
YES. AS PRACTICE. YOU HAVE TO START OUT LEARNING TO BELIEVE THE LITTLE LIES.
"So we can believe the big ones?"
YES. JUSTICE. MERCY. DUTY. THAT SORT OF THING.
"They're not the same at all!"
YOU THINK SO? THEN TAKE THE UNIVERSE AND GRIND IT DOWN TO THE FINEST POWDER AND SIEVE IT THROUGH THE FINEST SIEVE AND THEN SHOW ME ONE ATOM OF JUSTICE, ONE MOLECULE OF MERCY. AND YET—Death waved a hand. AND YET YOU ACT AS IF THERE IS SOME IDEAL ORDER IN THE WORLD, AS IF THERE IS SOME...SOME RIGHTNESS IN THE UNIVERSE BY WHICH IT MAY BE JUDGED.
"Yes, but people have got to believe that, or what's the point—"
MY POINT EXACTLY.” — Terry Pratchett, the Hogfather -
MetaphysicsIf all you're discussing turns on the use of clear terms, you're discussing crap that doesn't mean anything.
Alice: Do I have a broken leg?
Bob: Well it depends how you define leg. We surely need a better understanding of legs before deciding something so important.
Alice: It seems Pinochet was a tyrant.
Bob: Well it depends how you define tyrant. So much of the atrocities depend on the nature of tyranny.
Too much attention payed to the nature of words, not enough to the nature of the world. -
Get Creative!i
seat gum
slammed door
exhaust horn
steps echo
a near gasp
street trash
blowing in Your wind -
"White privilege"I am not in the front lines any more, so I readily admit my impressions are hardly scientific. but it seems to me 'white priviledge' is still used, often, and with regularity, to include a shaming. And not jsut a shaming about, say, the ignorance of a white person about the advantages they have had, but a shaming for being white. Or someone else for being a man, per se. — Coben
I've heard that similar things happen in communities with a safe space policy. Sometimes it is easier to have a simplified narrative; for therapeutic or rhetorical purposes, but I think the accusations really should be evaluated based on the context and validity. If someone is rebuking someone else (performatively) with an accusation/branding of privilege, it might be rooted a well grounded belief (though not necessarily true) based on past experience even if it's wrong. -
Saint Augustine and his ban on cousin marriageI don't know what to make of this other than fucking your cousins helps Black Lives Matter.
-
"White privilege"But often it seems to be used as a shaming, a j'accuse on the individual level. — Coben
Think this is more to do with a wounded reaction to the term's use rather than anything to do with the systemic properties of privilege. Though, the wounded reaction's prevalence is something worthy of analysis in itself. -
"White privilege"White privilege is about the dominance of the white perspective? Sure, go for it. — Judaka
Not what I said. Ignores the socio-economic dimensions. I responded in a way that highlighted the epistemological angle to take on privilege because that's what you asked about in my post. I even stressed that the two are related in my post, too. No idea where you're getting this from. -
"White privilege"Yeah great but it's still not related to the term white privilege. — Judaka
This is lazy. Standpoint theory originated in intersectional approaches to feminism. Specifically, black women face different stuff to white ones. As an epistemology approach it applies whenever identity group differences influences perspective formation. If you'd read even the entire wiki article I'd linked you would see that. It explicitly has race examples.
If you want to see some of the links between the two here might help. The keyword is 'epistemic privilege'. -
"White privilege"I don't think white privilege is a term used to describe the differences in perspective or character between whites and coloured people. The term even has "privilege" in it and while what you have said, for the most part, is more or less true, I don't know how you figure that white privilege is a term that describes any of the things you've mentioned. — Judaka
Read about standpoint theory for the epistemological dimension. -
"White privilege"White privilege isn't a call for shame. It's not there to make people ashamed of being white. The idea is pretty banal and has sociological and epistemological variants, though they should not be emphasised independently.
The epistemological one:
(1) How people form perspectives is sensitive to under what conditions they grow up.
(2) Regularities in those conditions often lead to regularities in perspectives.
For the same structural reason that a homeless person rarely has to worry about their holiday expenditures, a white person rarely has to worry about the presence of police. At that point, you might say that whiteness-blackness, gender etc... are more superficial influences on perspective than something like homelessness. But that objection already accepts the framing device which is doing all the work; that social conditions can strongly influence perspective formation - perspectives are socially fungible. What matters now is how to answer the question of in what ways and if race alters perspective formation.
You can see that in attitudes towards police, differences in religious practice, attitudes towards education and communication styles. But all these differences in perspective; of how people form opinions and what opinions they form; make more sense upon the background of social context.
The sociological one:
(1) Members of social identity groups in the aggregate face different social pressures, economic conditions and are afforded opportunities differentially based on that identity group membership.
(2) Social identity is not something arbitrary, it comes from an interaction of statistical tendencies of individuals within identity groups.
Let's go to (2) first, someone is not gay just because they choose to identify as such, they are gay based off their sexual preferences. They might be treated as gay if they signal in a way correlated with the social expectations of the identity group, or if they really are gay and it's found out. Or schoolyard conspiracies, whatever.
In a similar way, someone is not 'black' just because of the colour of their skin, having black skin is a signifier highly correlated with social roles and expectations of being black. Black identity is a branding that comes with the skin; social expectations and expected norms of conduct and personality traits. Social processes read off a skin colour as if that procedure had any legitimacy, but it still happens. It's precisely that dynamic that makes it not arbitrary; the branding as a social process. Like the value 'branded' on currency ultimately through common use thereof.
And (1) is just a simple empirical question, though actually answering it requires looking at the data. The short answer is; yes it does happen, a lot, and in every way you'd expect and some you wouldn't. The long answer is: racial identity, even though it's a social construct, is so highly correlated with other performance effecting metrics like education level and home and environment that it's difficult to establish any direct causal link between racial identity and performance. But the strength of the correlation between racial identity and these performance metrics is still reason enough to believe that there is differential treatment. -
We are responsible ONLY for what we do NOT controlUnder what conditions do people think morally?
Sometimes people orient their lives towards impersonal commandments and principles. A life lived with a higher calling or in a socially recognised cult.
Most of the time, people think morally when posed with moral problems. These aren't like the trolly problem, or debating whether lying is consistent with the categorical imperative. These are questions of how best to treat people, also of whether what one did is wrong and how to mitigate its effects. Under what conditions does someone care how best to treat someone? When they care, when they believe their influence matters, when their influence does in fact matter and such a state is discovered. That is, they are discovered in social contexts; family, friends, lovers, organisations. Belief in this regard is also embedded in interpersonal connection; a relation of people and people; rather than as a pro-attitude towards an ethical maxim. Such a belief might be called trust.
You can usually 'refute' an ethical maxim, "One ought to do X" or "One ought not to do X" by interpreting it literally and supplanting a contextual defeater. This is an intellectual game; it varies arbitrarily over contexts and people. It's a game of association between stated principles and subtended social contexts in which their expression contradicts the maxim as stated.
Where ethics happens is between people. Ethical thought is inspired by care of others. Care not just as an emotive state, but care as an ontological condition of interpersonal relationships. Care is what inspires terror when seeing a child play in traffic, "one should not play in traffic" as a maxim is a reified guide, however sensible.
This change of perspective, really a return to the perspective we have usually, of ethics being rooted in care induces a transformation of ethical thought to the development of heuristics which guide the praxis of interpersonal development. -
Volcanic Soils (rants on systems ontology)If we consider amylase itself as a self maintaining process; of folded proteins with their movements constrained to a geometry induced by their intermolecular forces; the amylase part of the amylase-starch system, going down from the amylase starch interaction catalysis renders the amylase just a bearer of an active site. The proximity of amylase and starch is what initiates their interaction, but they both are sensitive to the presence of the other. — fdrake
Cashing out this idea of sensitivity could be done in a few ways. If we're looking at the molecular dynamics of a distribution of amylase in solution binding to starch molecules in solution, an appropriate model would probably look something like:
, the probability depends on how near the active site is to the appropriate bit of the starch molecule. It would also probably depend on other things, like the relative velocities of the enzyme and the starch, the relative orientation of the two... Ideally this would capture all the dynamical variables of interest. But there's still the amylase-starch system to talk about in terms of its relationship to digestion (glucose metabolism), in which case what matters is the aggregate and presence of the interactive system of their molecular dynamics.
On this level, what matters is the enzyme's capacity to act as an environmental filter for starch molecules, and how efficiently (energetically/productively) it can catalyse their breakdown. What matters is the 'on/off' property of 'has this produced simpler sugars?' and what is selected over reproductively are the protein configurations of the enzymes which facilitate this transformation. The specifics of those protein configurations are blurred; the sigma algebra of amylase producing events realises into the aggregate variable of (more or less efficiently produced) simpler sugars. That is, they are selected for as a system of interacting with starch unto themselves. In other words; selection acts upon the interaction between amylase and starch by modifying amylase's open feed forward that becomes closed by starch's presence; a potential for a feed-forward (starch presence->amylase) becomes interactive feedback (starch <-> amylase catalysis). -
Volcanic Soils (rants on systems ontology)Any relationship to the ‘arche-fossil’? Am I getting warm? — Wayfarer
Maybe the only relation to the arche-fossil is that it tries to be a ground-clearing for thought like this. A demystification device, an impetus from idealism or correlationism to materialist thought. -
Volcanic Soils (rants on systems ontology)This post was originally titled "Enzymatic catalysis as a model of causality". A rough description of how enzymes work in general is that they're:
(1) A bunch of proteins in a certain shape.
(2) The shape has a cavity called an 'active site'.
(3) The shape only fits things resembling it closely.
What an active site does is temporarily bond to some chemical to induce a chemical reaction to it. The chemical can make the enzyme fit to it by how it interacts with it, but that doesn't matter much here. A canonical example in humans is amylase in saliva, which takes starches; long chain polymers of carbohydrates; and acts at the carbohydrate-carbohydrate bonds to produce smaller carbohydrates to start their digestion.
The amylase is just there in human saliva. The starch is just there in food. When we chew, the proximity of the starches in our food and the amylase induces the breakdown reaction.
Amylase has sensitivity to the presence of certain carbohydrate bonds; it then acts on them when they are close. The internal dynamics of the amylase molecule facilitate the breakdown of starches into smaller carbohydrates. From the point of view of digestion, what matters is the efficiency of the breakdown relative to evolutionary-ecological-amylase productive constraints rather than the specifics of the molecular structure of amylase. They are a machine which solves the initial problem of starch digestion.
When giving a description of the amylase-starch system, however, what matters is the active site-chemical interaction. From that you can consider the various molecular and geometric structures that an enzyme may have as directions of variation which may be selected for; the specifics blur out, what matters is the feed forward of simple carbohydrates from complex carbohydrates.
But what of amylases that are not currently omnomnoming their starch? They are sensitive and specific to the presence of starches. Consistent with the previous themes in this thread; causality is always an interactive process, sensitivities are open feed forwards, but now we have enzymatic specificity; they only work on one thing, their mechanism as enzymes is sensitive only to starch presence, they have a single developmental trajectory in terms of starch - the production of smaller carbohydrates. (though stuff sufficiently similar can block enzyme functioning!)
When a system has a sensitivity, the system can be controlled or influenced by manipulating that sensitivity. Like a bridge to torsion (so make structures which resist it), inside temperature of a fridge to outside temperature of the room (make thermometers and variable cooling mechanisms). A sensitivity is a direction of variation which is open to (active site) the presence of a feed forward (starch presence); and a feed forward is the name of a realised interaction from some external system.
If we consider amylase itself as a self maintaining process; of folded proteins with their movements constrained to a geometry induced by their intermolecular forces; the amylase part of the amylase-starch system, going down from the amylase starch interaction catalysis renders the amylase just a bearer of an active site. The proximity of amylase and starch is what initiates their interaction, but they both are sensitive to the presence of the other.
(enzymatic catalysis of starch breakdown)
(presence of active site)
Prosaically, the wisdom in the phrase "3/4 of success is just showing up" is reflected in the causal structure of enzymes; when amylase shows up at the starch of the day, they do their job simply by proximity to it. -
I don't like Mondays(I think philosophy channels similar energies less destructively. We only question a hammer when it breaks, we only question an economy of meaning for similar reasons. I sometimes think about what would have come of me if, when my bubble burst, I didn't have the capacity to slowly put stuff back together novelly in a meaning-arid space.) — csalisbury
I think you can do philosophy in a way which inspires transformation of whatever domain you're dealing with; I think another way of doing it is more exegetical and rooted in wonder, travelling along some domain and chronicling what's there. The two aren't mutually exclusive of course, but I think they can be.
Probably not super relevant to OP. -
I don't like Mondaysits a challenge to the official, avowed, economy of meaning. — csalisbury
I think it must be remembered that school shooters are just as embedded in this economy of meaning; only they seem challenged enough by it to act as they do. I imagine, though I have little to no data supporting this, that such acts of domestic terrorism are acts of revenge against (scapegoating representations of aspects of) that economy of meaning. Localised at their centre of trauma, or a symbolic representation of it. -
Volcanic Soils (rants on systems ontology)A model of a system typically contains parameters; variables of interest which capture dynamics within it. Parameters are directions of variation of a system. For seed germination, these parameters are moisture level, temperature and sunlight level. But how do seeds become sensitive to changes in and levels of these parameters in terms of their germination?
One part of the story conceives a seed as an evolutionary machine in an environment which affords seeds different reproductive successes based on its conditions. But the seed is in an entire environment, from the molecule to the climate, a complex system saturated with causal flows. The reproductive success rates of seeds benefit from internalising indicators of the flows that matter for their reproductive success; a seed becomes a map of its environment insofar as the environment interacts with the sensitivities of the seed.
But those sensitivities are distinguished somehow; how an environment interacts with a seed in terms of reproductive success is a constrained story told with few of the directions of variation available to the environment. These directions of variation embed themselves in the seed in an indicative form through modifying their reproductive success rates; a seed has attuned and will attune to what is relevant in its environment through the population level reproductive successes. It dances on the stage of its environment like a green idiot to music beyond its reckoning, but like us it learns to tell stories of its environment. So too for the bodies of their ancestors. Which parameters are relevant for them are those which are contained in the stories.
Relevance and irrelevance to reproductive success induces a sortal on the environment; a partition of its behaviour into that which counts-as relevant for the seed's reproductive success and that which does not. We can imagine an environment as a series of cycles; seasons, diurnal patterns of animals, weather in those seasons, rain crystallising in spider webs; some are sensitive to others, some are not. We should take from the seed example that something can only become relevant to the dynamics of a system when a causal flow can take something in the background as a given; a flow not in friction with something that varies sufficiently slowly with it. The subtended land soil forms over, those tectonic ingresses surrounded by water; is bedrock both literally and metaphorically for the cycles of the environment it subtends. It is not without change, just without change relative to the processes it supports. It is that relative changelessness which supports the ability for a system to separate itself from its environment; when a butterfly flaps its wings tornados move more than light.
The same can be said for the seed-bearing organismal sensitivity to light, moisture, temperature, it is a slower direction of variation relative to the sensory innovations of seeds to those sensitivities. When one follows a cladistic tree back in time, one sees not what is unchanging and essential, but what perturbations become reproduced; what contingencies are embedded in a flow of biomass reproduction that can become its moving (really becoming) parts. Essence is stability reified as given in a being; essence as a property forgets the becoming of its subtended sortal; it unasks the questions of what and how flows become partitioned into relevance and irrelevance for that being.
But when one treats not even essence as a given; and conceives it as a stability born from a partition of flows into relevant (learned sensitivity, destructive ignorance) and irrelevant (true causal isolation, statistical independence of flows) for a given flow; one therefore has to ask where in the flow does the capacity for such partition arise.
Relevance is a contour of interactive intensity; sensitivities are sites of intense interaction. Sensitivities are directions of variation which matter. -
I don't like Mondayscompassion for people who do bad things — T Clark
Yes. Compassion good. That kind of article that portrays high school shooters as misunderstood loners in need of love, not so good. No one's ever been around for that.
fdrake

Start FollowingSend a Message
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum

