Yes, it seems like mathematics has really taken a turn for the worse. If you really believe that mathematicians are aware of this problem, why do you think they keep heading deeper and deeper in this direction of worse? I really don't think they are aware of the depth of the problem — Metaphysician Undercover

Yes, it certainly looks like that faulty brick in the foundations of math will surely cause the giant structure to collapse. I wish I had known this before becoming a mathematician. :cry:

If we can know God perfectly, we can prove everything in mathematics once we fully know him and Godel's theorem will not apply. — Gregory

If you were to know God perfectly, mathematics is irrelevant. Especially if that "everything" includes things that mere mortals have deemed false. Just relax and savor the bliss. :love:

. . . when physicists talk about infinity they usually mean something entirely different than the way mathematicians use the term. They usually do mean unbounded — fishfry

I side with the physicists on this.

A philosopher of mathematics might consider this a serious issue. However, many mathematicians ignore it. But who knows about the future?

Remember, math is not like constructing a skyscraper, putting in a firm foundation before building the edifice. In math the edifice was largely in place, and the foundations were added afterwards.

Gowers: "The “two cultures” I wish to discuss will be familiar to all professional mathematicians.Loosely speaking, I mean the distinction between mathematicians who regard their central aim as being to solve problems, and those who are more concerned with building and understanding theories"

This is very well said. Of course the distinctions are not clean cut. And the following resonates:

Atiyah: "Some people may sit back and say, “I want to solve this problem” and they sit down and say, “How do I solve this problem?” I don’t. I just move around in the mathematical waters, thinking about things, being curious, interested, talking to people, stirring up ideas; things emerge and I follow them up. "

Now if we are filled with divine knowledge in a mystical experience, why would Godel's argument prove we couldn't prove all of mathematics while in that state of rapture. — Gregory

What are thoughts that we should capture
While in the throes of blissful rapture
That soothe the pain of incomplete
With certain knowledge
Now replete

And, modern physics looks at time as the fourth dimension of space — Metaphysician Undercover

A bit of vaudeville relief :lol:

Partly, philosophy at present supervenes on enormous amounts of knowledge - scientific and otherwise - unlike anything philosophers of the 18th century could imagine. When a physicist talks about string theory, I consider that modern day philosophy, although others might not. Even philosophical discussions on subjects like race require in-depth studies involving considerable data analysis to be substantial.

:up:

If it predicts it ain't metaphysics

If an axiom is false then the proof is unsound — Metaphysician Undercover

Is it possible for an axiom to be false? Please explain. Don't refer to inconsistency. :roll:

These postulates match up with the axioms. — frank

Axioms and postulates are generally considered the same things. Does Tononi distinguish between them?

So you agree with Tonini — frank

It's Giulio Tononi. :roll:

Tonini uses the axioms . . . — frank

It's Tononi. His system has as axiomatic the existence of consciousness. I agree and have the same perception of time. Both simply exist. And unraveling qualia or dissecting time seems wasted effort.

I write all my graphics with Liberty BASIC language, then insert the images in Word documents, then convert to pdf. I'm not familiar with other programs or services. Others who post on this forum might know of something.

Well, it sounds like people are working on it. I suppose I question attempting to apply math in this context. A lot depends on whether predictions are calculated and match reality. :chin:

From Wiki: "The calculation of even a modestly-sized system's Φ Max {\displaystyle \Phi ^{\textrm {Max}}} {\displaystyle \Phi ^{\textrm {Max}}} is often computationally intractable,[6] so efforts have been made to develop heuristic or proxy measures of integrated information. For example, Masafumi Oizumi and colleagues have developed both Φ ∗ {\displaystyle \Phi ^{*}} {\displaystyle \Phi ^{*}}[7] and geometric integrated information or Φ G {\displaystyle \Phi ^{G}} {\displaystyle \Phi ^{G}},[8] which are practical approximations for integrated information. These are related to proxy measures developed earlier by Anil Seth and Adam Barrett.[9] However, none of these proxy measures have a mathematically proven relationship to the actual Φ Max {\displaystyle \Phi ^{\textrm {Max}}} {\displaystyle \Phi ^{\textrm {Max}}} value, which complicates the interpretation of analyses that use them. They can give qualitatively different results even for very small systems.[10]

A significant computational challenge in calculating integrated information is finding the Minimum Information Partition of a neural system, which requires iterating through all possible network partitions. To solve this problem, Daniel Toker and Friedrich T. Sommer have shown that the spectral decomposition of the correlation matrix of a system's dynamics is a quick and robust proxy for the Minimum Information Partition.["

I looked into this briefly several years ago and recall that, apart from conceptual issues, the math is difficult to employ.

The bee/train problem is slightly different from my recollection, but basically the same ideas:Bee vs Trains
The process doesn't end before the trains collide, or, in my version, before the train hits the wall.

You still have not clearly explained the problem. Tell us exactly what x, y, t, d, and z represent. It sounds a bit like the old bee vs train problem where the bee keeps going back and forth at a constant rate between the moving train and the wall at the end of the track. That has a simple resolution.

Seems like a unusual question for one who started threads like "Qualia and Quantum Mechanics, The Sequel" and "Do Physics Equations Disprove the Speed of Light as a Constant?"

It doesn't make sense as posed. What you describe is a plane in 3-space. To see it , graph at 3D Grapher

The problem obviously, is that you, and mathematicians in general, according to what you said above, haven't got a clue as to what a number is. — Metaphysician Undercover

You neglected adding, "And you don't care!" :scream:

If I spent my time brooding over this issue I'd not get much math done. It's good there are gurus like you who are willing to navel gaze into this profound mystery and lay the foundations while we flitter about, inconsequential moths circling your flame.

Wikipedia has a relatively long article on the number 5. — fishfry

And it's even classified as Vital. There must be 10K pages on math on Wiki. I wonder how many are added each day?

It's a mystery to me. :chin:

Perhaps a non-Euclidean metric designed for entanglement, a novel metric space, could be a key to describing if not explaining the phenomenon. Maybe this has already been done. Just a passing thought.

Nice reply. Thanks.

Does that help? — sime

:roll:

Category theory is a popular mathematical area. An offshoot of algebra, it can be used as an alternative to establish the foundations of math. It searches for so-called universal properties in various categories. Personally, I find it alien and entirely non-productive in the nitty gritty stuff I study in complex variables.

The Wikipedia page for Category theory gets 575 views/day, a respectable number. The page you linked gets 5 views/day and is classified as low priority (like my math page). So it may not help. But good try.

I forgot to mention, one way a theorem could be considered "complete" is when the theorem is "sharp", which means the hypotheses cannot be reduced and the theorem still reach the conclusion. Numerical analysis is an area where one used to see this idea play out.

Reproductive Universe

Can you explain this, as I'm quite interested? — Shawn

Well, Shawn, you asked for it. Sorry, buddy, it's convoluted and I doubt comprehensible. I don't usually go to professional math sites like StackExchange, preferring to do the job myself, but I don't think it would make any difference for this particular problem. So I'll put it up here. And one of the math people on the forum might have a suggestion:

Start with a sequence of complex functions: $\left\{ {{f}_{k}} \right\}_{k=2}^{\infty }$,
And create a second sequence: ${{F}_{k-1,n}}(z)={{f}_{k-1}}\left( {{F}_{k,n}}(z) \right)$, ${{F}_{n,n}}(z)=z$ Which can be written as: ${{F}_{1,n}}(z)=z+{{\rho }_{1}}{{\varphi }_{1}}\left( {{F}_{2,n}}(z) \right)+{{\rho }_{2}}{{\varphi }_{2}}\left( {{F}_{3,n}}(z) \right)+\cdots +{{\rho }_{n-1}}{{\varphi }_{n-1}}\left( {{F}_{n,n}}(z) \right)$

${{\varphi }_{k}}(z)=-zQ(z)/\left( 1+{{\rho }_{k}}Q(z) \right),Q(z)=xCos(y)+iySin(x)$


Then show $\underset{n\to \infty }{\mathop{\lim }}\,{{F}_{1,n}}(z)$ exists.

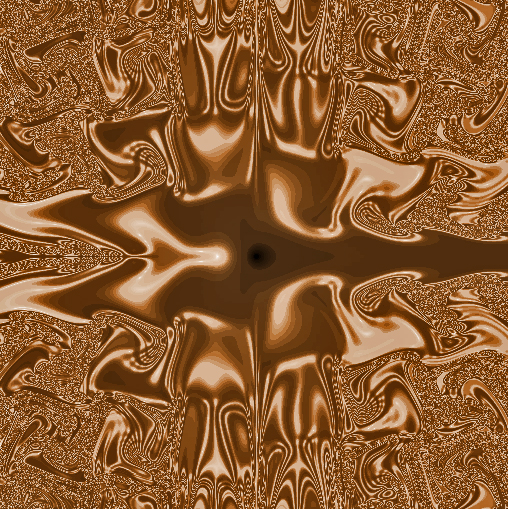
There have been discussions on this thread about recursive objects. Here's a Lulu from actual math, not about math. :cool:

This dynamical system is associated with an image I will post.

I just came across this quote from Mathematics Made Difficult by Linderholm. It points to the spirit of modern set theory and foundations :cool: :

“The days when one could get up from the dinner-table and leave the room at the mention of the Axiom of Choice are gone with the wind, and we must accustom ourselves to the new ways, the ways of tomorrow.”

And I don't know why Algebra is placed between them on that tree — TonesInDeepFreeze

An algebraist drew the tree?

You are not making two points on a plane into one point on the plane. You are moving to a point in another topology based on equivalence classes of the original points.

There still seems to be a little confusion about a priori vs a posteriori approaches to these ideas - at least for me. The notion of an automated theorem prover doing its job, and then the complexity of the proof being determined, seems quite distant from a program simply counting symbols and logical steps in existing proofs. But I can understand how an ATP might function under the guidance of a mathematician.

However, the idea that I could take the theorem I am trying to prove right now and turn it over to an ATP is far fetched. Although appealing, I must admit. I am at the point that there might be the slightest possibility it falls into the Godel Hole, since I find that to prove the conjecture seems to require that I assume the conjecture, a circular trap. I'm not speaking of an indirect proof. All my computer experiments suggest it is true. :worry:

I'm curious. As a retired prof I don't think it's accurate.

Here's another:

Length & Complexity

I'm wondering about reaching out on somewhere like Stack Exchange for more information or how to answer it — Shawn

That's a possibility, but be prepared for some confusion about what you are asking. You're in a different ball game on that forum.

A machine for ascertaining the length of the shortest proof of a theorem doesn't involve anything like oracles — TonesInDeepFreeze

A posteriori I assume? Not a priori.

I find it interesting as a mathematical question onto itself. — TonesInDeepFreeze

True enough. Beyond my pale.

I sort of dread the notion of making mathematics more formal. :scream:

Interesting ideas, but to my mind it's putting the cart before the horse. I don't see how this sort of knowledge would help prove a theorem, which is the essence of mathematics. But then the very idea of theorem proving as a programming exercise is foreign to me. However, I use the computer all the time for imagery and examples which may point the way forward in my deliberations. My age, I suppose.