-
 Pierre-Normand
2.9kThe part to note is that almost all of this is a red herring. Its irrelevant if she remembers or not. Its just word play to get us out of the raw math. The odds are still the same.
Pierre-Normand
2.9kThe part to note is that almost all of this is a red herring. Its irrelevant if she remembers or not. Its just word play to get us out of the raw math. The odds are still the same.
Flip heads, 1 result
Flip tails, 2 results
Put the pile of results as total possible outcomes. You have 3 possible outcomes. In two of the outcomes, tails was flipped. Put it in a hat and draw one. You have a 2/3rd chance that its a tails outcome.
To be clear, it is a 50/50 shot as to whether heads or tails is picked. Meaning that both are equally like to occur. But since we have more outcomes on tails, and we're looking at the probability of what already happened based on outcomes, not prediction of what will happen, its a 2/3rds chance for tails. — Philosophim
The issue with her remembering or not is that if, as part of the protocol, she could remember her Monday awakening when the coin landed tails and she is being awakened again on Tuesday, she would be able to deduce that the coin landed Tails with certainty and, when she couldn't remember it, she could deduce with certainty that "today" is Monday (and that the probability of Tails is 1/2). That would be a different problem, and no problem at all.
Your argument in favor of the Thirder credence that the coin landed Tails (2/3) relies on labeling the awakening episodes "the outcomes". But what is it that prevents Halfers from labelling the experimental runs "the outcomes" instead? Your ball picking analogy also has been produced by Berry Groisman to illustrate this ambiguity in his The end of Sleeping Beauty's Nightmare paper (although I don't fully agree with his conclusions). -
 Philosophim
3.5kThe issue with her remembering or not is that if, as part of the protocol, she could remember her Monday awakening when the coin landed tails and she is being awakened again on Tuesday, she would be able to deduce that the coin landed Tails with certainty and, when she couldn't remember it, she could deduce with certainty that "today" is Monday — Pierre-Normand
Philosophim
3.5kThe issue with her remembering or not is that if, as part of the protocol, she could remember her Monday awakening when the coin landed tails and she is being awakened again on Tuesday, she would be able to deduce that the coin landed Tails with certainty and, when she couldn't remember it, she could deduce with certainty that "today" is Monday — Pierre-Normand
Correct. My point was that its just used as a word problem way of saying, "We have 3 outcomes we reach into a hat and pull from"
Your argument in favor of the Thirder credence that the coin landed Tails (2/3) relies on labeling the awakening episodes "the outcomes". But what is it that prevents Halfers from labelling the experimental runs "the outcomes" instead? — Pierre-Normand
Because there are two different outcomes. One with one day, and one with two days. If you pick any day and have no clue if its a day that resulted from a heads or tails outcome, its a 2/3rds chance its the tails outcome. The heads and tails is also irrelevant. The math is, "Its as equally likely that we could have a series of one day or two day back to back in this week. If you pick a day and you don't know the outcome or the day, what's the odds its a tails day vs a heads day?"
The odds of whether its head or tails is irrelevant since they are the same and can be effectively removed from the problem. -
 Pierre-Normand
2.9kCorrect. My point was that its just used as a word problem way of saying, "We have 3 outcomes we reach into a hat and pull from" — Philosophim
Pierre-Normand
2.9kCorrect. My point was that its just used as a word problem way of saying, "We have 3 outcomes we reach into a hat and pull from" — Philosophim
You are using the word "outcome" ambiguously and inconsistently. In your previous post you had stated that "You have 3 possible outcomes. In two of the outcomes, tails was flipped."
And now you are saying that:
Because there are two different outcomes. One with one day, and one with two days. If you pick any day and have no clue if its a day that resulted from a heads or tails outcome, its a 2/3rds chance its the tails outcome. The heads and tails is also irrelevant. The math is, "Its as equally likely that we could have a series of one day or two day back to back in this week. If you pick a day and you don't know the outcome or the day, what's the odds its a tails day vs a heads day?"
The odds of whether its head or tails is irrelevant since they are the same and can be effectively removed from the problem.
So, now you are back to treating experimental runs rather than awakening episodes as the "outcomes". This sort of ambiguity indeed is the root cause of the misunderstanding that befalls Halfers and Thirders in their dispute.
When Sleeping Beauty is being asked, on one particular awakening occasion, what her credence is that the coin landed Tails, she must ponder over what the odds are that the epistemic situation she currently is in (given the information available to her) is such that the coin landed Tails when she is in that situation. In other words, she takes herself to be experiencing one among a range of possible and undistinguishable (from her current point of view) events (or "outcomes") such that a proportion P of them occur when the coin landed Tails, in the long run. All of this leaves it undefined what the events or "outcomes" are that we're talking about.
Thirders interpret those outcomes as awakening episodes and Halfers interpret them as experimental runs. Their expressed credences, 2/3 and 1/2 respectively, therefore are answers to different questions (or to the same question differently disambiguated, if you will).
Thirder Sleeping Beauty expects, reasonably enough, that in the long run awakening episodes like the one she is currently experiencing will turn out to have occurred when the coin had landed Tails two thirds of the time.
Halfer Sleeping Beauty expects, equally reasonably, that, in the long run, experimental runs like the one she is currently experiencing (regardless of how many more times she already was or will be awakened during that run) will turn out to have occurred when the coin had landed Tails one half of the times.
Credences implicitly are about ratios. Halfers and Thirders disagree about the denominator that is meant to figure in the relevant ratio. -
 Philosophim
3.5kSo, now you are back to treating experimental runs rather than awakening runs as the "outcomes". This sort of ambiguity indeed is the root cause of the misunderstanding that befalls Halfers and Thirders in their dispute. — Pierre-Normand
Philosophim
3.5kSo, now you are back to treating experimental runs rather than awakening runs as the "outcomes". This sort of ambiguity indeed is the root cause of the misunderstanding that befalls Halfers and Thirders in their dispute. — Pierre-Normand
I'm not seeing the ambiguity here, but maybe I'm not communicating clearly. There are two outcomes based on context.
1 Outcome of the coin
2. Outcome from the result of the coin
The outcome from the coin is always 50/50. Because of this, you can ignore the outcome and simply say, "Its equally likely that the result of one coin flip will happen as the other result"
When we look at all the outcomes from the result of the coin, we see that if its tails, there are two days, and only 1 day if heads. So if you don't know which day it is, (previous days can be removed as we 'forget') then it is a 1/3 chance that your day is a heads, and 2/3rd chance that your day is a tails. Is it equally likely that a heads or a tails was flipped in isolation from the days? Yes. But since we have different outcomes from the flip itself, we have to take them all in consideration and realize that if either side is equally likely to occur, it is a much better odds to say that its heads because the consequence of it being heads makes it twice as likely you awake two days.
One more way to think about it is you have a hat that you could either reach in one time, or two times. Each is equally likely to occur. You forget how many times you've reached into the hat. Is it more likely that you're on an outcome where you reach in two times, or one time? Obviously its two times. -
 Pierre-Normand
2.9kI'm not seeing the ambiguity here, but maybe I'm not communicating clearly. There are two outcomes based on context. — Philosophim
Pierre-Normand
2.9kI'm not seeing the ambiguity here, but maybe I'm not communicating clearly. There are two outcomes based on context. — Philosophim
I assume what you now mean to say is that there are two possible ways to think of the "outcomes" based on context. Well, sure, that's pretty much what I have been saying. But I'm also arguing that the original Sleeping Beauty problem fails to furnish the relevant context.
If we think of the experimental runs following the coin toss as the "R-outcomes" (an equal amount of T-runs and H-runs are expected) and the awakening episodes as the "A-outcomes" (twice as many T-awakenings as H-awakenings are expected), then we've resolved part of the ambiguity. But Sleeping Beauty isn't being asked about specific kinds of outcomes explicitly. Rather she is being asked about her credence regarding the current state of the coin. She can reason that the current state of the coin is Tails if and only if she is currently experiencing a T-awakening and hence that the current state of the coin is twice as likely to be Tails than it is to be Heads. But she can also reason that the current state of the coin is Tails if and only if she is currently experiencing a T-run and hence that the current state of the coin is equally as likely to be Tails than it is to be Heads.
Another way to state the Halfer interpretation that makes it intuitive is to suppose Sleeping Beauty will be given a bag of Twizzlers (T-candy) at the end of the experiment if the coin landed Tails and a bag of Hershey's Kisses (H-candy) if it landed Heads. The fact that she's awakened twice rather than once when she's scheduled to receive Twizzlers doesn't make it more likely that she will receive them at the end of the run. Hence her credence remains 1/2 that she will receive Twizzlers. This is consistent with her credence being 2/3 that her current awakening episode (A-outcome) is twice as likely to be one that puts her on a path towards getting Twizzlers. But since the Twizzlers reward is an outcome that is being realized if and only if she is currently experiencing a T-awakening, she can sensibly reason that the odds of that are 1/2 also.
The key to understanding the consistency between the two apparently contradictory credences regarding the very same coin toss result is to realize that the two T-awakening outcomes occur in the same timeline and hence them being more frequent than H-awakenings doesn't increase the relative frequency of the Twizzlers rewards (or of her having experienced a T-run, regardless of how many times she was awakened in this run). -
 Philosophim
3.5kBut Sleeping Beauty isn't being asked about specific kinds of outcomes explicitly. Rather she is being asked about her credence regarding the current state of the coin. She can reason that the current state of the coin is Tails if and only if she is currently experiencing a T-awakening and hence that the current state of the coin is twice as likely to be Tails than it is to be Heads. But she can also reason that the current state of the coin is Tails if and only if she is currently experiencing a T-run and hence that the current state of the coin is equally as likely to be Tails than it is to be Heads. — Pierre-Normand
Philosophim
3.5kBut Sleeping Beauty isn't being asked about specific kinds of outcomes explicitly. Rather she is being asked about her credence regarding the current state of the coin. She can reason that the current state of the coin is Tails if and only if she is currently experiencing a T-awakening and hence that the current state of the coin is twice as likely to be Tails than it is to be Heads. But she can also reason that the current state of the coin is Tails if and only if she is currently experiencing a T-run and hence that the current state of the coin is equally as likely to be Tails than it is to be Heads. — Pierre-Normand
She can reason that its equally likely that the result of the coin flip is 50/50, but that doesn't mean its likely that the day she is awake is 50/50. Lets flip it on its head and note how the likelihood that she would be wrong.
If she always guesses heads, she's wrong twice if its tails. If she always guesses tails, she's only wrong once. Thus, she is twice as likely to be wrong if she guesses heads on any particular day woken up, and twice as likely to guess correctly if she guesses tails. If the total odds of guessing correctly were 50/50, then she would have an equal chance of guessing correctly. She does not.
We can see this by extending the days out. Lets say that if its heads, she's woken up one day. If its tails she's woken up 10 days. Again, its better odds to guess tails, despite the outcome of the coin being equal as mentioned above.
As I've been noting, because the probable outcome of the coin is the same, you can effectively remove the probable outcome of the coin from the equation. r = r can be divided out. Lets change up the odds of the coin flip, and it changes the our guess.
Going back to the original setup, lets Say that its twice as likely that the coin lands on heads. Now the probability of the coin becomes essential to the outcome of the follow up outcomes.
So its two times more likely that its heads, but only one day. 1 times as likely for two days. This appears to equate to 50/50 when considering what day is randomly picked out of the outcomes.
Now, there is absolutely zero doubt that in the original case it is not a 50/50 outcome. However, I do doubt if it ends up being 2/3rds. There may be some multiplicative statistical shenanigans needed here that I'm not aware of that is being disguised by making the heads/tails outcome equal and eliminating it as a consideration. Perhaps the imaginary case I made above would be more revealing of any special case. Thus I may be wrong that 2/3rds is the answer, but there is no question that 1/2 is wrong. -
 Pierre-Normand
2.9kShe can reason that its equally likely that the result of the coin flip is 50/50, but that doesn't mean its likely that the day she is awake is 50/50. — Philosophim
Pierre-Normand
2.9kShe can reason that its equally likely that the result of the coin flip is 50/50, but that doesn't mean its likely that the day she is awake is 50/50. — Philosophim
Sure, but the former precisely is what she is being asked. She is being asked what her credence about the coin will be on that occasion, and not what the proportion of such occasions are that are T-occasions. One can argue than she is being asked this implicitly, but in that case it's still open to interpretation what those "occasions" are meant to be, as we've already discussed.
Lets flip it on its head and note how the likelihood that she would be wrong.
If she always guesses heads, she's wrong twice if its tails. If she always guesses tails, she's only wrong once. Thus, she is twice as likely to be wrong if she guesses heads on any particular day woken up, and twice as likely to guess correctly if she guesses tails. If the total odds of guessing correctly were 50/50, then she would have an equal chance of guessing correctly. She does not.
That's right, and this is a good argument favoring the Thirder position but it relies on explicitly introducing
a scoring procedure that scores each occasion that she has to express her credence: once for each awakening episode. If you would rather score those statements only once per run, regardless of how many times she is being asked about her credence in that run, then she would be right half the times. This also makes sense if you view all of the separate awakening episodes occurring during a single Tails run to be part of the same "outcome" (as you've indeed yourself favored doing earlier). -
 Philosophim
3.5kSure, but the former precisely is what she is being asked. She is being asked what her credence about the coin will be on that occasion, and not what the proportion of such occasions are that are T-occasions. — Pierre-Normand
Philosophim
3.5kSure, but the former precisely is what she is being asked. She is being asked what her credence about the coin will be on that occasion, and not what the proportion of such occasions are that are T-occasions. — Pierre-Normand
I would say she is being asked what the odds are of it being a day in which a T side vs a H side coins is flipped. If she's only being asked what the percent chance of the coin ended up being at, the answer is always 50/50. The odds of the coin flip result don't change whether its 1 or 1,000,000 days. What changes is from the result of that coin flip, and that is the pertinent data that is important to get an accurate answer.
This is very similar to the old Monty Hall problem. You know the three doors, make a guess, then you get to make another guess do you stay or change?
On the first guess, its always a 1/3 shot of getting the door wrong. But it can also be seen as a 2/3 chance of getting the door wrong. When given another chance, you simply look at your first set of odds and realize you were more likely than not wrong, so you change your answer. The result matches the odds.
Same with the situation here. Run this experiment 100 times and have the person guess heads 50 times, then tails 50 times. The person who guesses tails every time 50 times will be right 2/3rds of the time more than the first. Since outcomes ultimately determine if we are correct in our odds, we can be confident that 1/2 odds is incorrect.
By the way, very nice discussion! I appreciate your insight and challenging me to view things I might not have considered. -
 Pierre-Normand
2.9kI would say she is being asked what the odds are of it being a day in which a T side vs a H side coins is flipped. — Philosophim
Pierre-Normand
2.9kI would say she is being asked what the odds are of it being a day in which a T side vs a H side coins is flipped. — Philosophim
I was talking about what she is being asked, literally, in the original formulation of the problem discussed in the OP. From Wikipedia:
This has become the canonical form of the problem: [...] During the interview Sleeping Beauty is asked: "What is your credence now for the proposition that the coin landed heads?"
Your reading is a sensible interpretation of this question, but it isn't the only one.
If she's only being asked what the percent chance of the coin ended up being at, the answer is always 50/50. The odds of the coin flip result don't change whether its 1 or 1,000,000 days. What changes is from the result of that coin flip, and that is the pertinent data that is important to get an accurate answer.
Yes, quite, but now with the phrase "the result of that coin flip" you still seem to be gesturing to the "occasions" being generated by those coin flip results. And how is it that those events are meant to be individuated (one occasion per run or one per awakening) is what's at issue.
This is very similar to the old Monty Hall problem. You know the three doors, make a guess, then you get to make another guess do you stay or change?
On the first guess, its always a 1/3 shot of getting the door wrong(sic). But it can also be seen as a 2/3 chance of getting the door wrong. When given another chance, you simply look at your first set of odds and realize you were more likely than not wrong, so you change your answer. The result matches the odds.
That's not quite how the Monty Hall problem is setup so I'm unsure about the analogy your intending to make. The contestant has a 1/3 chance of getting the prize-hiding door right on their first try. But the game host then reveals among the two other doors one that they (i.e. the host) know to be hiding a goat. The contestant then is being offered an opportunity to switch their initial choice for the other unopened door. The correct reasoning is that since contestants that switch their choices will win the prize on each occasion where their first choice was wrong, they have a 2/3 change of winning the prize if they switch their choice.
Same with the situation here. Run this experiment 100 times and have the person guess heads 50 times, then tails 50 times. The person who guesses tails every time 50 times will be right 2/3rds of the time more than the first. Since outcomes ultimately determine if we are correct in our odds, we can be confident that 1/2 odds is incorrect.
Yes, the person who guesses that the coin landed Tails will turn out to have made a correct guess two thirds of the times on average, thereby matching the Thirder credence. But the Halfer argues that this is just because they were able to make more guesses during T-runs. Under the Thirder interpretation of the meaning of SB's credence, though, her being afforded more opportunities to express her credence during T-runs doesn't make those runs more likely to happen, and this is what to them matter.
By the way, very nice discussion! I appreciate your insight and challenging me to view things I might not have considered.
Cheers! -
 JeffJo
175On the occasion of an awakening, what is Sleeping Beauty's expectation that when the experiment is over ... — Pierre-Normand
JeffJo
175On the occasion of an awakening, what is Sleeping Beauty's expectation that when the experiment is over ... — Pierre-Normand
This is what invalidates your variation. She is asked during the experiment, not before or after. Nobody contests what her answer should be before or after. And you have not justified why her answer inside the experiment should be the same as outside.
The issue with her remembering or not is that if, as part of the protocol, she could remember her Monday awakening when the coin landed tails and she is being awakened again on Tuesday, she would be able to deduce that the coin landed Tails with certainty and, when she couldn't remember it, she could deduce with certainty that "today" is Monday (and that the probability of Tails is 1/2). That would be a different problem, and no problem at all. — Pierre-Normand
Gee, if she is given a different set of information (knowing that it is not Tuesday, after Heads is information, as is all of these) produces different conditional probabilities. Possibly certainties. And?
Here's one more attempt. It's really the same thing that you keep dodging by changing the timing of the question, and claiming that I have "vallid thirder logic" while ignoring that it proves the halfer logic to be inconsistent.
- Get three opaque note cards.
- On one side of different cards, write "Monday and Heads," "Monday and Tails," and "Tuesday and Tails.
- Turn the cards over, shuffle them around, and write "A," "B," and "C" on the opposite sides.
- Before waking SB on the day(s) she is to be woken, put the appropriate card in the table in her room, with the letter side face up.
Let's say she sees the letter "B." She knows, as a Mathematical fact, that there was a 1/3 probability that "B" was assigned to the card with "Heads" written on the other side. And a 2/3 chance for "Tails."
By halfer logic, while her credence that "Heads" is written on the "B" card must be 1/3, her credence that the coin landed on Heads is 1/2. This is a contradiction - these two statements represent the same path to her current state of knowledge, regardless of what day it is.
Your justification for considering the halfer logic is that there may be a different path that _includes_ her her current state of knowledge and another that has a different day written on the card. My reason for rejecting that justification outright, besides the contradiction that it produces, is that this other day is not a path of the the path she sees. -
 Pierre-Normand
2.9kOn the occasion of an awakening, what is Sleeping Beauty's expectation that when the experiment is over ...
Pierre-Normand
2.9kOn the occasion of an awakening, what is Sleeping Beauty's expectation that when the experiment is over ...
— Pierre-Normand
This is what invalidates your variation. She is asked during the experiment, not before or after. Nobody contests what her answer should be before or after. And you have not justified why her answer inside the experiment should be the same as outside. — JeffJo
It looks like you didn't parse correctly the sentence fragment that you quoted. It is indeed on the occasion of an awakening (as I said) that she is being asked about her credence regarding the coin, not later. I did make reference in the question to the end-off-run verification conditions of the credence statement that SB is asked to express. The reason this reference is made (to the future verification conditions) is to disambiguate the sense of the question, in accordance with the Halfer interpretation in this case. But the question still is about her credence "now".
Compare: (1) "What are the chances, now, that your lottery ticket is the winning ticket?" and (2) "What are the chances, now, that your lottery ticket has the number that will be drawn as the winning number?" It's the exact same question and the odds are the same (one in a million, say). The second question merely makes explicit what "winning" means.
Here's one more attempt. It's really the same thing that you keep dodging by changing the timing of the question, and claiming that I have "vallid thirder logic" while ignoring that it proves the halfer logic to be inconsistent.
Get three opaque note cards.
On one side of different cards, write "Monday and Heads," "Monday and Tails," and "Tuesday and Tails.
Turn the cards over, shuffle them around, and write "A," "B," and "C" on the opposite sides.
Before waking SB on the day(s) she is to be woken, put the appropriate card in the table in her room, with the letter side face up.
Let's say she sees the letter "B." She knows, as a Mathematical fact, that there was a 1/3 probability that "B" was assigned to the card with "Heads" written on the other side. And a 2/3 chance for "Tails."
By halfer logic, while her credence that "Heads" is written on the "B" card must be 1/3, her credence that the coin landed on Heads is 1/2. This is a contradiction - these two statements represent the same path to her current state of knowledge, regardless of what day it is.
The Halfer logic is to reason that although T-runs, unlike H-runs, are such that SB will be presented with a card two different times (one on Monday and one on Tuesday), nevertheless, on each occasion where the experiment is performed and she finds herself being involved in an individual experimental run, the likelihood that this run is a T-run is 1/2. That's because in the long run there are as many T-runs as there are H-runs. By that logic she can also reason that, on an particular occasion where she is being awakened, the chances that she is holding the "Monday and Heads" card is 1/2. The fact that she now finds out her card to be labelled "B" doesn't alter those odds since the labelling procedure is probabilistically independent from the coin toss result and hence this result conveys no information to her regarding the coin toss result.
By the way, for the same reason, it would not convey any information to her either from a Thirder perspective. Her credence that the coin landed Tails would remain 2/3 before and after she saw the "B" label on her card.
Remember: SB isn't betting on the card (neither is she betting on the current awakening episode). She's betting on the current coin toss outcome. How those outcomes must be considered to map to her possible ways to experience them (in separate awakenings or separate runs) is a matter of interpretation that isn't spelled out in the original SB problem. It's true, though, that under the Thirder interpretation, betting on the wakening episodes or betting on the cards is equivalent. But that's just because the cards and the awakening episodes are mapped one-to-one. -
 JeffJo
175
JeffJo
175
Perhaps you didn't parse correctly. There is no ambiguity. If she is asked to project her state of knowledge on Wednesday, or to recall it from Sunday, of course the answer is 1/2.The reason this reference is made (to the future verification conditions) is to disambiguate the sense of the question, ... — Pierre-Normand
Where, exactly, do you think projection or recollection is implied or stated? You are forcing this issue into a place where it does not belong, in order to justify saying that 1/2 is a possible answer.
Remember: SB isn't betting on the card (neither is she betting on the current awakening episode). She's betting on the current coin toss outcome.
I keep looking at the problem, and I can't find a reference to betting anywhere. The reason I don't like using betting is because anybody can re-define how and when the bet is made and/or credited, in order to justify the answer they like. One is correct, and one is wrong.
They ask her one question after each time she awakens, however: What is the probability that the coin shows heads.
Do you see the words "landed when it was flipped" here? No? How about "will be showing after the experiment ends"? Still no? Then stop inserting them. What is the probability that the coin is showing "Heads"? This is in the present tense.
So, if a bet were to exist, and assuming she uses the same reasoning each time? She risks her $1 during the interview, and is credited her winnings then also. If she bets $1 on Heads with 2:1 odds, she gains $2 if the coin landed Heads, and loses 2*$1 if it landed on Tails. If she bets on Tails with 1:2 odds, she loses $1 if the coin landed Heads, and gains 2*$0.50=$1 if it landed Tails.
But if she bets $1 on Heads with 1:1 odds, she gains $1 if the coin landed Heads, and loses 2*$1=$2 if it landed on Tails. If she bets on Tails with 1:1 odds, she loses $1 if the coin landed Heads, and gains 2*$1=$2 if it landed Tails.
The answer, to the question that was asked and not what you want it to be, is 1/3. -
 Michael
16.6kHer Thirder-credence would then be pragmatically relevant to selecting the destination most likely to afford her a sunny trip. — Pierre-Normand
Michael
16.6kHer Thirder-credence would then be pragmatically relevant to selecting the destination most likely to afford her a sunny trip. — Pierre-Normand
Again, there's not much sense in this so-called "pragmatically relevant" credence. Even before being put to sleep – and even before the die is rolled – I know both that the die is most likely to not land on a 6 and that betting that it did will offer the greater expected return in the long run. So after waking up I can – and will – continue to know that the die most likely did not land on a 6 and that betting that it did will offer the greater expected return in the long run, and so I will bet against my credence.
With respect to "pragmatic relevance", Thirder reasoning is unnecessary, so if there's any sense in it it must be somewhere else.
Under the Thirder interpretation, all three of those biconditionally related "experienced" events are actual on average 2/3 of the times that SB is experiencing a typical awakening episode. — Pierre-Normand
My argument is that a rational person should not – and would not – reason this way when considering their credence, and this is most obvious when I am woken up 2101 times if the coin lands heads 100 times in a row (or once if it doesn't).
It is true that if this experiment were to be repeated 2101 times then we could expect of all awakenings to occur after the coin landed heads every time, but it's also irrelevant. The experiment is only performed once. I strongly believe that it is irrational for one's credence to consider this long term average; a rational person, after waking up and knowing that the experiment is only performed once, will only consider the sheer improbability of the coin landing heads every time. Their credence remains . There is no ambiguity in the question or the answer.
Thirder reasoning only has its place, if it has a place at all, if both a) the experiment is repeated 2101 times and b) Sleeping Beauty is also made to forget between experiments. It matters that the problem does not stipulate these two conditions. -
 Pierre-Normand
2.9kPerhaps you didn't parse correctly. There is no ambiguity. If she is asked to project her state of knowledge on Wednesday, or to recall it from Sunday, of course the answer is 1/2. — JeffJo
Pierre-Normand
2.9kPerhaps you didn't parse correctly. There is no ambiguity. If she is asked to project her state of knowledge on Wednesday, or to recall it from Sunday, of course the answer is 1/2. — JeffJo
I was explicitly referring to her state of knowledge at the time when the interview occurs. There is no projection of this state into the future. Likewise, when you buy a lottery ticket and express your credence that it is the winning ticket as one in one million, say, what you mean is that there is a one in one million chance that, when the winning number will be drawn (or will be revealed, if it has already been drawn), your ticket will be the winner. You're not projecting your state of knowledge into the future. You're merely stating the conditions of verification regarding what your present state of knowledge (i.e. your credence) is about.
I keep looking at the problem, and I can't find a reference to betting anywhere. The reason I don't like using betting is because anybody can re-define how and when the bet is made and/or credited, in order to justify the answer they like. One is correct, and one is wrong.
Establishing a betting protocol with a well defined payout structure enable SB to put her money where her mouth is, and also to clarifies what it is that her stated credence is about. It highlights the tension between saying that you have a high credence that some outcome is true but that you wouldn't bet on it. Once you acknowledge that it is rational to make an even money bet on an outcome that you believe to be more likely to occur (or to be actual) than not, then the specification of the payout structure help clarify what the stated credence is about (i.e. what it is exactly that you take to be most likely to occur, or to be actual). This indeed goes beyond the original statement of the problem, but since it is precisely my contention that the original statement is ambiguous, it's a useful way to highlight the ambiguity.
So, if a bet were to exist, and assuming she uses the same reasoning each time? She risks her $1 during the interview, and is credited her winnings then also. If she bets $1 on Heads with 2:1 odds, she gains $2 if the coin landed Heads, and loses 2*$1 if it landed on Tails. If she bets on Tails with 1:2 odds, she loses $1 if the coin landed Heads, and gains 2*$0.50=$1 if it landed Tails.
But if she bets $1 on Heads with 1:1 odds, she gains $1 if the coin landed Heads, and loses 2*$1=$2 if it landed on Tails. If she bets on Tails with 1:1 odds, she loses $1 if the coin landed Heads, and gains 2*$1=$2 if it landed Tails.
The answer, to the question that was asked and not what you want it to be, is 1/3.
Indeed, such a payout structure clarifies what the bettor means when they express a 2/3 credence that the the coin landed tails. They mean that the epistemic situations that they find themselves in when awakened are T-awakenings (as opposed to H-awakenings) two thirds of the time. A different payout structure that rewards the bettor only once when they place a winning bets during an experimental run clarifies what the bettor means when they express a 1/2 credence that the the coin landed tails. They mean that the epistemic situations that they find themselves in when awakened are T-runs (as opposed to H-runs) one half of the times. As @Michael correctly argues in defence of a Halfer interpretation, merely being afforded more opportunities to bet on a given ticket (outcome) doesn't make it any more likely that this ticket is the winning ticket (or that the outcome is actual). -
 Pierre-Normand
2.9kAgain, there's not much sense in this so-called "pragmatically relevant" credence. Even before being put to sleep – and even before the die is rolled – I know both that the die is most likely to not land on a 6 and that betting that it did will offer the greater expected return in the long run. So after waking up I can – and will – continue to know that the die most likely did not land on a 6 and that betting that it did will offer the greater expected return in the long run, and so I will bet against my credence.
Pierre-Normand
2.9kAgain, there's not much sense in this so-called "pragmatically relevant" credence. Even before being put to sleep – and even before the die is rolled – I know both that the die is most likely to not land on a 6 and that betting that it did will offer the greater expected return in the long run. So after waking up I can – and will – continue to know that the die most likely did not land on a 6 and that betting that it did will offer the greater expected return in the long run, and so I will bet against my credence.
With respect to "pragmatic relevance", Thirder reasoning is unnecessary, so if there's any sense in it it must be somewhere else. — Michael
It is indeed somewhere else. Look at the payout structure that @JeffJo proposed in their previous post. Relative to this alternative payout structure, your own Halfer reasoning is unnecessary.
My argument is that a rational person should not – and would not – reason this way when considering their credence, and this is most obvious when I am woken up 2^101 times if the coin lands heads 100 times in a row (or once if it doesn't).
It is true that if this experiment were to be repeated 2^101 times then we could expect 2/3 of all awakenings to occur after the coin landed heads every time, but it's also irrelevant.
It's only irrelevant to the determination of your credence about the experimental run that you are experiencing (regarding what proportion of such runs are T-runs). Regarding the determination of your credence about the specific awakening episode that you are experiencing, though, it's rather the fact that T-runs and H-runs are equally frequent that is irrelevant. Taking the case to such wild extremes, though, makes your intuition about the comparative utility of betting on such unlikely outcomes (i.e. H-awakenings) relative to the utility of betting on the likeliest outcome (T-awakenings) play into your intuition about the rational credence. (Why would anyone risk a virtually guaranteed and useful $1 for an infinitesimal chance of winning a bazillion dollars that one wouldn't even be able to stash away in a Sun-sized vault?) But that just a psychological fact. Using more sensible win/loss ratios of 2/3 vs 1/3, or 6/11 vs 5/11 in the die case, doesn't reveal anything odd about the Thirder interpretation of her credence, or about her betting behavior.
[/quote]Thirder reasoning only has its place, if it has a place at all, if both a) the experiment is repeated 2^101 times and b) Sleeping Beauty is also made to forget between experiments. It matters that the problem does not stipulate these two conditions.[/quote]
The experiment needs no be repeated many times for SB's expression of her 2/3 credence (under the Thirder interpretation of her credence) to make sense, or for her associated betting behavior to be rational. The case of a single experimental run (following a single coin flip) was addressed specifically in my Leonard Shelby Christmas gift case. You can refer to it for the relevant Bayesian updating calculations, but here is another variation that may be more intuitive:
For this year’s annual cocktail party at the Sleeping Beauty Experimental Facility, Leonard Shelby is among the guests. Drinks are being served by two butlers: Alfred and Lurch. Each guest is entitled to three complimentary drinks.
In Leonard's case, as with every other guest, a fair coin is secretly tossed beforehand. If the coin lands Tails, Alfred is assigned to serve him two of his drinks and Lurch one. If it lands Heads, their roles are reversed: Lurch serves two drinks and Alfred one. The guests are informed of this protocol, and Leonard has made a note of it in his memento notepad.
Because of his anterograde amnesia, Leonard cannot keep track of how many drinks he has already received, if any. Nor does he initially recognize either butler by name, but he can read their name tags when they approach him.
A final feature of the protocol is that, at the end of the evening, guests whose coin landed Tails (and thus received two drinks from Alfred and one from Lurch) will be given a bag of Twizzlers ("T-candy"). Those whose coin landed Heads will receive a bag of Hershey’s Kisses ("H-candy").
At any given moment during the party, when Leonard sees a butler bringing him a drink, his credence that this drink is unique (that is, not one of two planned drinks from the same butler) is 1/2, as is his credence that the coin landed Heads. However, upon reading the name tag and discovering that the butler is Alfred, he updates his credence that the coin landed Tails to 2/3, since there are twice as many situations in which the coin landed Tails and Alfred serves him a drink as there are situations where the coin landed Heads and Alfred serves him one. This mirrors the Thirder interpretation in the Sleeping Beauty problem.
That seems straightforward enough until someone asks him, "So, Leonard, do you think you’ll get Twizzlers or Kisses at the end of the night?"
He frowns, checks his notepad, and realizes that by the same reasoning that gave him 2/3 for Tails a moment ago, he ought also to think he's more likely than not to get Twizzlers. But that can't be right. The coin decides both outcomes, doesn’t it?
The trick, of course, is in what Leonard’s belief precisely is about when he thinks about the coin toss "outcome". When he reasons about this drink—the one Alfred is serving him—he’s locating himself among drink-moments. In that frame, a Tails-run simply generates twice as many such moments involving Alfred. But when he wonders what candy he'll get later, he's no longer locating himself in a drink-moment but in an entire "run of the evening": the single history that will end either in Twizzlers or Kisses. And there, each run counts only once, no matter how many times Alfred appeared in it.
Two T-drinks in a Tails-run correspond to just one Twizzlers outcome (in the same timeline), while one H-drink in a Heads-run corresponds to one Kisses outcome. Once you factor that mapping in, the overall odds of Twizzlers or Kisses even out again. (Since experiencing one of two T-drink event doesn't exclude but rather ensures the actuality of the other T-drink event in the same timeline).
So Leonard’s probabilities fit together neatly after all. In the middle of the party, as Alfred hands him a glass, he can think, "This is probably a T-drink". Yet, looking ahead to the end of the night, he can just as honestly write in his notebook, "Chances of T-candy: fifty-fifty." -
 JeffJo
175
JeffJo
175
Uh, yeah?Your argument in favor of the Thirder credence that the coin landed Tails (2/3) relies on labeling the awakening episodes "the outcomes". — Pierre-Normand
Write "Heads and Monday" on one notecard. Write "Tails and Monday" on another, and "Tails and Tuesday" on a third. Turn them over, and shuffle them. Then write "A," B," and "C" on the other sides.
Pick one. What is the probability that it says "Heads" on the other side? What is the probability that it says "Tails" on the other side? Call me silly, but I'd say 1/3 and 2/3, respectively.
Each morning of the experiment when SB is to be awakened, put the appropriate card on a table in her room, with the letter side up. Hold the interview at that table.
What is the probability that the card, regardless of what letter she sees, says "Heads" on the other side? Or "Tails?" This "outcome" can be defined by the letter she sees. But that does not define what an outcome is, being the description of the experiment's result, in SB's knowledge, is. If she wakes on a different day, that is a different result. Being determined by the same coin flip does not determine that.
Now, did these probabilities change somehow? For which letter(s) do they change? Or are they still 1/3 and 2/3?
Within SB's knowledge, is not the outcome where it says "Heads" the exact same outcome where the coin is showing Heads? And the same with "Tails?" If it says "Tails and Monday," is there not another interview along this same path where it says "Tails and Tuesday?" Does that change the probability that this card says "Tails?" How does that carry over to the one time it would say "Heads?"
Again, halfers are constructing inconsistent logic to support the answer they desire. Not using valid logic to answer the question.
Because it is not both Monday, and Tuesday, when she is asked the question? What else may or may not happen is irrelevant.But what is it that prevents Halfers from labelling the experimental runs "the outcomes" instead?
A "scoring procedure" based on imagined repeats is a way of testing your probabilities, not of defining it. It does not work in the SB problem, as should be painfully obvious, because each side will define the number of trials differently since repeated runs require looking at more than one outcome, and the number changes based on the subject event.That's right, and this is a good argument favoring the Thirder position but it relies on explicitly introducing a scoring procedure that scores each occasion that she has to express her credence: once for each awakening episode. — Pierre-Normand -
 Pierre-Normand
2.9kWrite "Heads and Monday" on one notecard. Write "Tails and Monday" on another, and "Tails and Tuesday" on a third. Turn them over, and shuffle them. Then write "A," B," and "C" on the other sides.
Pierre-Normand
2.9kWrite "Heads and Monday" on one notecard. Write "Tails and Monday" on another, and "Tails and Tuesday" on a third. Turn them over, and shuffle them. Then write "A," B," and "C" on the other sides.
Pick one. What is the probability that it says "Heads" on the other side? What is the probability that it says "Tails" on the other side? Call me silly, but I'd say 1/3 and 2/3, respectively.
Each morning of the experiment when SB is to be awakened, put the appropriate card on a table in her room, with the letter side up. Hold the interview at that table.
What is the probability that the card, regardless of what letter she sees, says "Heads" on the other side? Or "Tails?" This "outcome" can be defined by the letter she sees. But that does not define what an outcome is, being the description of the experiment's result, in SB's knowledge, is. If she wakes on a different day, that is a different result. Being determined by the same coin flip does not determine that.
Now, did these probabilities change somehow? For which letter(s) do they change? Or are they still 1/3 and 2/3? — JeffJo
In the first case you described, a single run of the experiment consists in randomly picking one of three cards. When an outcome is determined, the remaining two possibilities collapse, since the three are mutually exclusive.
In the second case, which mirrors the Sleeping Beauty protocol more closely, two of the possible outcomes, namely "Monday & Tails" and "Tuesday & Tails," are not mutually exclusive. In modal logical terms, one is "actual" if and only if the other is, even though they do not occur at the same time. This is unlike the relationship either has to "Monday & Heads," which is genuinely exclusive. Picking "Monday & Tails" guarantees that "Tuesday & Tails" will be picked the next day, and vice versa. They are distinct events but belong to the same timeline. One therefore entails the other.
It’s precisely this relation of entailment, rather than exclusion, that explains why the existence of two separate occasions for Sleeping Beauty to find herself in a Tails-awakening does not dilute the probability of her finding herself in a Heads-timeline, on the Halfer interpretation.
In other words, one third of her awakenings are "Mon & Tails," one third are "Tue & Tails," and one third are "Mon & Heads," vindicating her 1/3 credence that her current awakening is a Heads awakening. But since the two "Tails" awakenings always occur sequentially within the same timeline, they jointly represent two occasions for her to experience a single Tails-run: one that remains just as frequent as a Heads-run overall.
Thus the "Thirder credence" in Heads outcomes (1/3) and the "Halfer credence" in Heads timelines (1/2) are both valid, but they refer to different ratios: the first to occasions of experience, the second to timelines of outcomes. Crucially, this is true even though on both accounts the target events (whether awakenings or timelines) occur if and only if the coin landed Heads. -
 Michael
16.6kRelative to this alternative payout structure, your own Halfer reasoning is unnecessary. — Pierre-Normand
Michael
16.6kRelative to this alternative payout structure, your own Halfer reasoning is unnecessary. — Pierre-Normand
Yes, I have tried to argue this point several times. A rational person's credence in the outcome of the coin toss is unrelated to the betting strategy that yields the greater expected return in the long run, and is why any argument to the effect of "if I bet on Tails then I will win bets, therefore my credence that the coin landed on Tails is " is a non sequitur. The most profitable betting strategy is established before being put to sleep when one’s credence is inarguably , showing this disconnect.
After waking up you just either believe that the coin most likely landed on Tails or you don't, and I think my extreme example shows that no rational person’s credence will be based on some counterfactual ratio of awakenings in the way that Thirders say. It seems absurd for anyone to answer anything other than , regardless of how you “choose” to interpret the question. -
 Pierre-Normand
2.9kYes, I have tried to argue this point several times. A rational person's credence in the outcome of the coin toss is unrelated to the betting strategy that yields the greater expected return in the long run, and is why any argument to the effect of "if I bet on Tails then I will win 2/3 bets, therefore my credence that the coin landed on Tails is 2/3" is a non sequitur. The most profitable betting strategy is established before being put to sleep when one’s credence is inarguably 1/2, showing this disconnect. — Michael
Pierre-Normand
2.9kYes, I have tried to argue this point several times. A rational person's credence in the outcome of the coin toss is unrelated to the betting strategy that yields the greater expected return in the long run, and is why any argument to the effect of "if I bet on Tails then I will win 2/3 bets, therefore my credence that the coin landed on Tails is 2/3" is a non sequitur. The most profitable betting strategy is established before being put to sleep when one’s credence is inarguably 1/2, showing this disconnect. — Michael
Your argument is too quick and glosses over essential details we already rehearsed. We agreed that when there are two mutually exclusive outcomes A and B, there isn’t a valid inference from "I am rationally betting on outcome A" to "My credence in A is highest." But that’s not because there is no rational connection between betting strategies and credences. It’s rather because, as we also seemed to agree, the rational choice of a betting strategy depends jointly on your credences in the outcomes and the given payout structure. Hence, if the cost of placing a bet is $1, and if my credence in Tails being realized whenever I place a bet is twice my credence in Heads being realized on such occasions, and the payout structure is such that I’m paid $2 each time I’ve placed a bet when the coin lands Tails, then it’s rational for me to bet on Tails. The reason why it’s rational is that (1) I am paid back $2 each time I place such a bet and (2) I expect Tails to be realized twice as often on occasions such as the present one when I place a bet (my credence), which yields an expected value of $1.33. The second consideration therefore remains part of the equation.
What a Halfer would typically object to (and you yourself have sometimes argued) is that this has no bearing on SB’s credence regarding the odds that the coin landed Tails for her current experimental run (as determined by the coin toss), which credence is independent of the number of awakenings (or betting opportunities) that occur during that run. They can illustrate this with a payout structure that awards $2 per experimental run regardless of SB’s number of guessing opportunities. In that case, SB rationally expects to break even because (1) she expects the Tails outcome to be realized just as frequently as the Heads outcome across runs (regardless of how many times she is awakened within a run) and (2) the payout structure (matching the odds of the outcome being realized while a bet was placed) nullifies the expected value.
In summary, rational credence doesn’t float free of betting; it aligns with whatever gets checked. If we check one answer per run, rational calibration yields 1/2. If we check one answer per awakening, rational calibration yields 2/3 (or 6/11 in the die case). The same coin is being talked about, but the Halfer and Thirder interpretations of SB’s credence refer to different scorecards. Given one scorecard and one payout structure, everyone agrees on the rational betting strategy in normal cases. I’ll address your extreme case separately, since it appeals to different (nonlinear) subjective utility considerations. -
 JeffJo
175
JeffJo
175
Oh? You mean that a single car can say both "Monday & Tails" and "Tuesday & Tails?" Please, explain how.In the second case, which mirrors the Sleeping Beauty protocol more closely, two of the possible outcomes, namely "Monday & Tails" and "Tuesday & Tails," are not mutually exclusive. — Pierre-Normand
"What is your credence in the fact that this card says "Heads" on the other side? This is unquestionably 1/3.
"What is your credence in the fact that the coin is currently showing Heads?" This is unquestionably an equivalent question. As is ""What is your credence in the fact that the coin landed on Heads/i]?"
I realize that you want to make the question about the entire experiment. IT IS NOT. I have shown you over and over again how it leads to contradictions. Changing the answer between these is one of them.
Now, the fact that the coin shows Tails on Tuesday, if a question can be asked, certainly is the same fact as it was on Monday. But SB's knowledge set does not allow a connection between these.
And how is this relevant to SB?In modal logical terms, one is "actual" if and only if the other is
No. BECAUSE ONE EXISTS IN HER "WORLD," AND THE OTHER DOES NOT.even though they do not occur at the same time.
And how does this affect what SB's credence should be, when she does not have access to any information about "timelines?"Picking "Monday & Tails" guarantees that "Tuesday & Tails" will be picked the next day, and vice versa. They are distinct events but belong to the same timeline. One therefore entails the other.
AGAIN: You are constructing invalid and inconsistent logic to support the conclusion you want to reach. -
 Pierre-Normand
2.9kOh? You mean that a single car can say both "Monday & Tails" and "Tuesday & Tails?" Please, explain how. — JeffJo
Pierre-Normand
2.9kOh? You mean that a single car can say both "Monday & Tails" and "Tuesday & Tails?" Please, explain how. — JeffJo
I was referring to your second case, not the first. In the first case, one of three cards is picked at random. Those three outcomes are mutually exclusive by construction. In your second case, the three cards are given to SB on her corresponding awakening occasions. Then, if the coin lands Tails, SB is given the two T-cards on two different days (Mon & Tue). So "Mon & Tails" and "Tue & Tails" are distinct events that both occur in the same timeline; they are not mutually exclusive across the run, even though each awakening is a separate moment.
"What is your credence in the fact that this card says "Heads" on the other side? This is unquestionably 1/3.
"What is your credence in the fact that the coin is currently showing Heads?" This is unquestionably an equivalent question. As is ""What is your credence in the fact that the coin landed on Heads/i]?"
I realize that you want to make the question about the entire experiment. IT IS NOT. I have shown you over and over again how it leads to contradictions. Changing the answer between these is one of them.
I also take the question to always be about the coin. You are arguing that this translates into a question about the card (or awakening episode) on the ground that there is a biconditional relation that holds between coin outcomes and awakening (or card) outcomes. On any occasion of awakening, the coin landed Heads if and only if the awakening is a H-awakening and this happens if and only if "Monday & Heads" is written on the card. But a Halfer will likewise argue that on any occasion of awakening during a run, the coin landed Heads if and only if the run is a H-run. The fact that SB is awakened twice during a T-run, or given two cards, doesn't alter this. Just like you are arguing that the question isn't about the runs, the Halfer argues that it isn't about the awakenings either.
"Picking "Monday & Tails" guarantees that "Tuesday & Tails" will be picked the next day, and vice versa. They are distinct events but belong to the same timeline. One therefore entails the other." —Pierre-Normand
And how does this affect what SB's credence should be, when she does not have access to any information about "timelines?"
She does have the information that the two potential T-awakenings occur on the same timeline and that the H-awakening occurs on a different one. This is an essential part of the experiment's protocol that SB is informed about. The Halfer argues that since the two T-awakenings occur on the same timeline (on two successive days) the two occasions that SB finds to experience a T-awakening don't dilute the probability that she could be experiencing an H-timeline.
What Halfers and Thirders both overlook is that the timeline branching structure set up by the Sleeping Beauty protocol establishes both equal (1/3) frequencies of the three types of awakening (Monday&Heads, Monday&Tails and Tuesday&heads) and equal (1/2) frequencies of the two types of experimental runs (Tails-runs and Heads-runs). This makes it possible to individuate the events Sleeping Beauty is involved in in two different ways. Sleeping beauty can therefore say truly that she is currently experiencing an awakening that she expects, in the long run, to be one among three equally frequent types of awakening (and therefore has a 2/3 chance of being a T-awakneing) and also say truly that she is currently experiencing an experimental run that she expects, in the long run, to be one among two equally frequent types of runs (and therefore has a 1/2 chance of being a T-run). The apparent contradiction comes from neglecting the two-to-one mapping of T-awakenings to T-runs within the same timeline.
In both interpretations, it's the coin outcome that is at issue but, when expressing a credence about this outcome, tacit reference always is made to the epistemic situations SB finds herself in while evaluating the relative frequencies of her encounters with those outcomes. The statement of the original SB problem doesn't specify what constitutes "an encounter": an experimental run or a singular awakening? Halfers and Thirders intuitively individuate those events differently, although those intuitions often are grounded in paradigmatic cases that are extensions of the original problem and that make one or the other interpretation more pragmatically relevant. -
 JeffJo
175I was referring to your second case, not the first. In the first case, one of three cards is picked at random. Those three outcomes are mutually exclusive by construction. In your second case, the three cards are given to SB on her corresponding awakening occasions. Then, if the coin lands Tails, SB is given the two T-cards on two different days (Mon & Tue). So "Mon & Tails" and "Tue & Tails" are distinct events that both occur in the same timeline; they are not mutually exclusive across the run, even though each awakening is a separate moment. — Pierre-Normand
JeffJo
175I was referring to your second case, not the first. In the first case, one of three cards is picked at random. Those three outcomes are mutually exclusive by construction. In your second case, the three cards are given to SB on her corresponding awakening occasions. Then, if the coin lands Tails, SB is given the two T-cards on two different days (Mon & Tue). So "Mon & Tails" and "Tue & Tails" are distinct events that both occur in the same timeline; they are not mutually exclusive across the run, even though each awakening is a separate moment. — Pierre-Normand
And.... you continue to ignore the obvious point I am making. You keep looking at an "outcome" as what occurs over two days. The only "outcome" SB sees occurs on one day.
But if you really want to use two days, do it right. On Tails, there are two waking days. On Heads, there is a waking day and a sleeping day. The sleeping day still exists, and carries just as much weight in the probability space as any of the waking days. What SB knows is that she is in one of the three waking days.
Each day carries a 1/4 prior probability. Since SB knows she is in a waking day, the sleeping day is "eliminated" and she can use conditional probability to update the probabilities of the three waking days to 1/3 each. And it is no different than if you always wake SB, but have three interview days and one DisneyWorld day. The three days that have a common description, when that common description is what SB sees, each have a probability of 1/3. This is true regardless of what the other one description is.
And you have offered no counter arguments except "but what if SB wants to look across all of the days." -
 Pierre-Normand
2.9kBut if you really want to use two days, do it right. On Tails, there are two waking days. On Heads, there is a waking day and a sleeping day. The sleeping day still exists, and carries just as much weight in the probability space as any of the waking days. What SB knows is that she is in one of the three waking days. — JeffJo
Pierre-Normand
2.9kBut if you really want to use two days, do it right. On Tails, there are two waking days. On Heads, there is a waking day and a sleeping day. The sleeping day still exists, and carries just as much weight in the probability space as any of the waking days. What SB knows is that she is in one of the three waking days. — JeffJo
Sure, but Sleeping Beauty isn’t being asked what her credence is that "this" (i.e. the current one) awakening is a T-awakening. She’s being asked what her credence is that the coin landed Tails. If you want to equate those two questions by the true biconditional "this awakening is a T-awakening if and only if the coin landed Tails" (which you are free to do), then you ought to grant the Halfer the same move: "This run is a T-run if and only if the coin landed Tails." And since the protocol generates T-runs and H-runs in equal frequency, her experiencing T-runs is as frequent as her experiencing H-runs.
Crucially, the fact that Sleeping Beauty sleeps more in H-runs has no bearing on the Halfer’s point. Arguing otherwise is like saying your lottery ticket is more likely to win because (in a setup where winning causes more "clutching opportunities") you’re allowed to clutch it more often (or sleep less) before the draw. That setup creates more opportunities to clutch a winning ticket and hence makes each "clutching episode" more likely to be a "T-clutching," but it doesn’t make the ticket more likely to win. And with amnesia, you can’t just count clutchings, or awakenings, to infer the outcome. -
 JeffJo
175Sure, but Sleeping Beauty isn’t being asked what her credence is that "this" (i.e. the current one) awakening is a T-awakening. — Pierre-Normand
JeffJo
175Sure, but Sleeping Beauty isn’t being asked what her credence is that "this" (i.e. the current one) awakening is a T-awakening. — Pierre-Normand
She is asked for her credence. I'm not sure what you think that means, but to me it means belief based on the information she has. And she has "new information." Despite how some choose to use that term, it is not defined in probability. When it is used, it does not mean "something she didn't know before," it means "something that eliminates some possibilities. That usually does mean something about the outcome that was uncertain before the experiment, which is how "new" came to be applied. But in this situation, where a preordained state of knowledge eliminates some outcomes, it still applies. -
 Pierre-Normand
2.9kShe is asked for her credence. I'm not sure what you think that means, but to me it means belief based on the information she has. And she has "new information." Despite how some choose to use that term, it is not defined in probability. When it is used, it does not mean "something she didn't know before," it means "something that eliminates some possibilities. That usually does mean something about the outcome that was uncertain before the experiment, which is how "new" came to be applied. But in this situation, where a preordained state of knowledge eliminates some outcomes, it still applies. — JeffJo
Pierre-Normand
2.9kShe is asked for her credence. I'm not sure what you think that means, but to me it means belief based on the information she has. And she has "new information." Despite how some choose to use that term, it is not defined in probability. When it is used, it does not mean "something she didn't know before," it means "something that eliminates some possibilities. That usually does mean something about the outcome that was uncertain before the experiment, which is how "new" came to be applied. But in this situation, where a preordained state of knowledge eliminates some outcomes, it still applies. — JeffJo
One important thing Sleeping Beauty gains when she awakens is the ability to make de re reference to the coin in its current state as the current state of "this coin" (indexically or deictically) whereas prior to awakening she could only refer to future states of the coin de dicto in a general descriptive way. To express her current credence (in light of her new epistemic situation) when awakened, she must also refer to her own epistemic position relative to the coin. We can appeal to David Lewis’s notion of de se reference (centered possible worlds). That’s what you seemed to have in mind earlier when you spoke of awakening events existing in "her world."
With this de se act, SB doesn’t merely locate herself at a single moment. In order to state her credence about the "outcome" in her centered world, she must also fix the unit over which probability mass is assigned: that is, how the total probability space (normalized to 1) is partitioned into discrete possible situations she might find herself in and that each have their own probabilities. Partitioning by awakening episodes is one such choice (the Thirder’s). It yields probability 1/3 for each one of the three possible occasions of encountering the coin in a definite state on a specific day. Crucially, this awakening-centered measure does not preclude the Halfer’s run-centered measure; it entails it, since the three awakening-centered worlds (and their frequencies) map in a fixed way onto the two run-centered worlds the Halfer is tracking (two-to-one in the case of T-worlds and one-to-one in the case of H-worlds).
Hence, the premises and reasoning SB uses to justify her 1/3 credence in Heads (including her knowledge of the two-to-one mapping from T-awakening-centered worlds to T-run-centered worlds) show that the Halfer credence is perfectly consistent and, in fact, supported by the very structure you endorse. The Thirder and Halfer credences about the same coin having landed Heads (1/3 vs 1/2) are consistent beliefs that implicitly refer to different centered world measures over the same underlying possibility space. -
 JeffJo
175SB "locates" herself in one of the four possible states in the experiment. These states exist whether or not she would be able to observe them, That was the point of the Camp Sleeping Beauty experiment: the 36 possible "days" each have a prior probability of 1/36. If she participates in activity "A", the probability that the die rolled N is the number of times A appears in row N, divided by the number of times A appears in the 6tx6 calendar. This is true if all activities are waking activities, or if one is a sleeping activity she would not be able to observe. Her observation is that B, C, D, E, and F did not occur, not just that A occurred.
JeffJo
175SB "locates" herself in one of the four possible states in the experiment. These states exist whether or not she would be able to observe them, That was the point of the Camp Sleeping Beauty experiment: the 36 possible "days" each have a prior probability of 1/36. If she participates in activity "A", the probability that the die rolled N is the number of times A appears in row N, divided by the number of times A appears in the 6tx6 calendar. This is true if all activities are waking activities, or if one is a sleeping activity she would not be able to observe. Her observation is that B, C, D, E, and F did not occur, not just that A occurred.
This is what determines the "probability mass." You correctly described how it is used, but you refuse to identify it correctly. I think you agreed (its hard to recall with all your pedantry) that this is true when all activities are waking ones, but I don't recall you addressing how sleeping activities affect it.THEY DON'T.
The "halfers run-centered measure" is precluded because you can't define, in a consistent way, how or why they are removed from the prior. So you avoid addressing that. -
 Pierre-Normand
2.9khe "halfers run-centered measure" is precluded because you can't define, in a consistent way, how or why they are removed from the prior. So you avoid addressing that. — JeffJo
Pierre-Normand
2.9khe "halfers run-centered measure" is precluded because you can't define, in a consistent way, how or why they are removed from the prior. So you avoid addressing that. — JeffJo
The Halfer's run-centered measure just is a way to measure the space of probabilities by partitioning the events that Sleeping Beauty's credence (understood as a ratio of such events) are about that are counted in the numerator and denominator. It refers to the expected proportion of runs Sleeping Beauty finds herself in that are H-runs or T-runs consistently with the information available to her at any given moment (such as an occasion of awakening).
Because there are two different ways (i.e. two different kinds of T-awakenings) for her to awaken in a T-run (on Monday or Tuesday) and only one to awaken in a H-run (on Monday), and the expected long term proportion of awakenings that are T-awakenings is 2/3, it is tempting to infer that the probability that she is experiencing a T-run likewise is 2/3. But while this is true in a sense it is also false in another sense.
It is indeed true, in a sense, that when she awakens the probability (i.e. her rational credence) that she is currently experiencing a T-run is 2/3. Spelled out explicitly, this means that SB expects, in the long run, that the sort of awakening episode she is experiencing is part of a T-run two thirds of the time. In a different sense, the probability that when she awakens she is currently experiencing a T-run is 1/2. Spelled out explicitly, this means that SB expects, in the long run, that the sort of experimental run she is experiencing is a T-run (and hence comprises two awakenings) half of the time. Notice that the first use of "the time" in "half of the time" meant half of the runs, while in "two thirds of the time", it meant two thirds of the awakenings.
The reason why there is no need for Sleeping Beauty to update her credence from 1/2 to 2/3 when her credence is understood in the "Halfer" way spelled out above is because nothing specific about her epistemic situation changes such that the proportion of such situations (runs) that are T-runs changes. That's true also in the case of her Thirder-credence. She already knew before the experiment began that she could expect to be awakened in a T-awakening situation two thirds of the time, and when she so awakens, nothing changes. So, her expectation remains 2/3. The fact that the Halfer-expectation matches the proportion of Tails coin toss results, and the Thirder-expectation doesn't, is fully explained by the fact that Tails coin toss results spawn two awakenings in one run while Heads coin toss results spawn a single awakening in one run.
Notice also that your removal of the non-awakening events (i.e. "Heads&Sunday") from the prior only yields a renormalisation of the relevant probabilities without altering the proportions of T-runs to H-runs, or of T-awakenings to H-awakenings, and hence without altering probabilities on either interpretation of SB's credence. Halfers and Thirders "condition" on different events, in the sense they they use those events as measures, but neither one does any Bayesian updating on the occasion of awakening since no new relevant information, no new condition, comes up. -
 ssu
9.7kThanks for @JeffJo for the resurrection of this thread.
ssu
9.7kThanks for @JeffJo for the resurrection of this thread.
I do think this related to the Monty Hall problem where information affects probabilities. Information does affect probabilities, you know. It's easier indeed to understand the Monty Hall when there's a lot more doors (just assume there's one million of them). So there's your pick from one million doors, then the gameshow host leaves just only one other door closed and opens all other 999 998 doors. You think it's really fifty-fifty chance then? You think you are so lucky that you chose the right door from a million?
If she knows the experiment, then it's the 1/3 answer. In Monty Hall it's better to change your first option as the information is different, even if one could at first think it's a 50/50 chance. Here it's all about knowing the experiment.
In this case it's a bit blurred in my view with saying that she doesn't remember if she has been already woken up. Doesn't mean much, if she can trust the experimenters. But in my view it's the same thing. Does it matter when she is represented with the following picture of events?
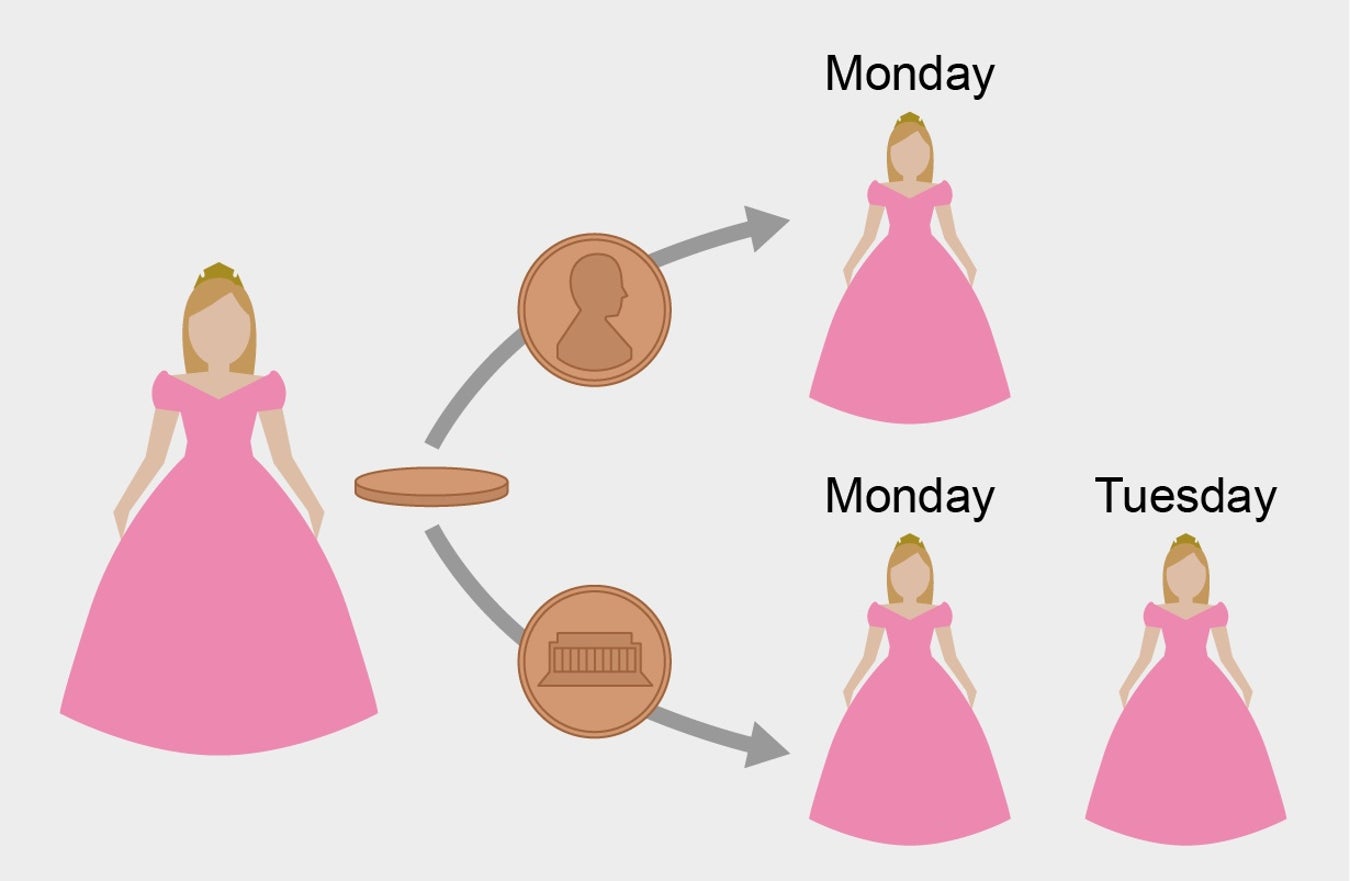
She cannot know exactly what day it is, of course. She can only believe that the information above is correct. Information affects probabilities, as in the Monty Hall problem.
What if these so-called scientists behind the experiment are perverts and keep intoxicating the poor woman for a whole week? Or a month? If she believes that the experiment ended on Wednesday, but she cannot confirm it being Wednesday, then the could have taken the been experiment for a week. Being drugged for a week or longer will start affecting your health dramatically.
Now I might have gotten this wrong, I admit. But please tell me then why I got it wrong. -
 Pierre-Normand
2.9kI do think this related to the Monty Hall problem where information affects probabilities. Information does affect probabilities, you know. It's easier indeed to understand the Monty Hall when there's a lot more doors (just assume there's one million of them). So there's your pick from one million doors, then the gameshow host leaves just only one other door closed and opens all other 999 998 doors. You think it's really fifty-fifty chance then? You think you are so lucky that you chose the right door from a million?
Pierre-Normand
2.9kI do think this related to the Monty Hall problem where information affects probabilities. Information does affect probabilities, you know. It's easier indeed to understand the Monty Hall when there's a lot more doors (just assume there's one million of them). So there's your pick from one million doors, then the gameshow host leaves just only one other door closed and opens all other 999 998 doors. You think it's really fifty-fifty chance then? You think you are so lucky that you chose the right door from a million?
If she knows the experiment, then it's the 1/3 answer. In Monty Hall it's better to change your first option as the information is different, even if one could at first think it's a 50/50 chance. Here it's all about knowing the experiment. — ssu
In the classic Monty Hall problem, since the three doors hide one prize and two goats, there is a 1/3 chance that the initially randomly selected door hides the prize. After the game show host deliberately opens one of the remaining two doors that they know not to contain the prize, the player can update their credence (probability estimate) that the remaining unselected door hides the prize to 2/3 and hence is incentivized to switching. It's not just the player's knowledge of the game protocol that embodies the relevant information, but also the actual action the game show host. This action leave the player's credence in their initial choice being right at 1/3 and hence yields no information regarding the initially selected door. But this action also yields knowledge about the two other doors: the one that has been shown to hide a goat now has zero chances of hiding the prize and the remaining unselected door now has a 2/3 chance of hiding it.
The simplest rationale for switching stems from the consideration that never switching makes the player win 1/3 of the time while always switching makes them win in all cases where they would otherwise lose (and vice versa), and hence makes them win 2/3 of the time.
Unlike the Sleeping Beauty Problem, the Monty Hall Problem isn't a matter of controversy in probability theory. Pretty much everyone agrees that after the game show host opens a goat-hiding door, the player is incentivized to switch their initial choice and thereby increases their chance from 1/3 to 2/3.
In this case it's a bit blurred in my view with saying that she doesn't remember if she has been already woken up. Doesn't mean much, if she can trust the experimenters. But in my view it's the same thing. Does it matter when she is represented with the following picture of events?
She cannot know exactly what day it is, of course. She can only believe that the information above is correct. Information affects probabilities, as in the Monty Hall problem.
What if these so-called scientists behind the experiment are perverts and keep intoxicating the poor woman for a whole week? Or a month? If she believes that the experiment ended on Wednesday, but she cannot confirm it being Wednesday, then the could have taken the been experiment for a week. Being drugged for a week or longer will start affecting your health dramatically.
Now I might have gotten this wrong, I admit. But please tell me then why I got it wrong.
What makes the Sleeping Beauty Problem harder, and more controversial, than the Monty Hall Problem is that despite agreeing about the game experiment protocol, disagreements arise regarding the meaning of Sleeping Beauty's "credence" about the coin toss result when she awakens, and also about the nature of the information she gains (if any) when she is awakened and interviewed.
In order assess if you're right or wrong, you'd need to commit to an answer and explains why you think it's right. Should Sleeping Beauty express a 1/2 credence, when she is being awakened, that the coin landed heads? Should it be 1/3, or something else? -
 Kizzy
165
Kizzy
165
AH-HA moment! See underlined part of JeffJo's quote.I was referring to your second case, not the first. In the first case, one of three cards is picked at random. Those three outcomes are mutually exclusive by construction. In your second case, the three cards are given to SB on her corresponding awakening occasions. Then, if the coin lands Tails, SB is given the two T-cards on two different days (Mon & Tue). So "Mon & Tails" and "Tue & Tails" are distinct events that both occur in the same timeline; they are not mutually exclusive across the run, even though each awakening is a separate moment. — Pierre-Normand
And.... you continue to ignore the obvious point I am making. You keep looking at an "outcome" as what occurs over two days. The only "outcome" SB sees occurs on one day.
But if you really want to use two days, do it right. On Tails, there are two waking days. On Heads, there is a waking day and a sleeping day. The sleeping day still exists, and carries just as much weight in the probability space as any of the waking days. What SB knows is that she is in one of the three waking days.
Each day carries a 1/4 prior probability. Since SB knows she is in a waking day, the sleeping day is "eliminated" and she can use conditional probability to update the probabilities of the three waking days to 1/3 each. And it is no different than if you always wake SB, but have three interview days and one DisneyWorld day. The three days that have a common description, when that common description is what SB sees, each have a probability of 1/3. This is true regardless of what the other one description is.
And you have offered no counter arguments except "but what if SB wants to look across all of the days." — JeffJo
In response to this specific part of your comment quoted above, "Each day carries a 1/4 prior probability. Since SB knows she is in a waking day, the sleeping day is "eliminated" and she can use conditional probability to update the probabilities of the three waking days to 1/3 each,"
I want to ask:
SB knows that Monday waking is guaranteed, no matter what the outcome of the coin toss, if so how can she eliminate the sleeping day and update the probabilities or her credence to 1/3...how is the conditional probability used to update the probabilities of the three waking days to 1/3 each? Monday waking offers no "new information" if it was guaranteed to happen from the start. She knows the rules. From what does she take from the inevitable waking day to update her credence besides confirming uncertainty?
From SB's pov, waking Monday was always going to happen. It doesn't update her credence, but Tuesday would...Just because SB cannot tell which day it is doesn't mean each day carries the same intel or informational value.so when those events aren't occurring in a way that is causally (and probabilistically) independent of the coin flip result. — Pierre-Normand
When she is awake, what knowledge does she have, related to any other day or coin result?
This is what seems difficult to accept. SB's "world" consists of one day, and one coin result, and due to the amnesia both are independent of any other "world" represented in another awakening. Illustrating that was the point of my "Camp Sleeping Beauty" variation. — JeffJo
In order assess if you're right or wrong, you'd need to commit to an answer and explains why you think it's right. Should Sleeping Beauty express a 1/2 credence, when she is being awakened, that the coin landed heads? Should it be 1/3, or something else? — Pierre-Normand
On Monday she always wakes - no matter what the coin says. So waking Monday tells her nothing new. On Tuesday, she only wakes if the coin landed tails. That is an experience conditional to the result and it is information...So there seems to be some ranking or levels to the importance or significance of the intel
Monday: inevitable, guaranteed, offers no/very little intel
Tuesday: outcome dependent, charged with intel (intel that we can even smell taste feel see or sense)
Since SB doesn't remember Monday, she cannot feel the difference but the structure of the experiment KNOWS the difference.So if she is asked twice, Monday and Tuesday, that only happens with tails outcome. Even without memory, her credence may shift, but because the setup itself is informative.
Monday-----> credence stays 1/2
Tuesday-----> credence shifts towards tails
Not sure what day it is???-------->maybe 1/3 but only as a reflection of uncertainty
Perhaps the structure of the experiment does not support equal weighing of awakenings and because of this, not treating all awakenings equally happens because not all carry the same weight of intel.
I wonder now, if it is not about counting awakenings but which ones actually help SB figure things out. This is about belief systems we adopt, the values we hold, and the decisions we make....even when we dont remember why exactly. The problem shows indirectly we are building beliefs, holding expectations, and how we reason when memory fails us as subjects embedded within a structure we lean on more than we may notice...what structures, ethical systems, cultural norms, personal values, systems of beliefs, with or without religious backed faith, intuition, to back up our reasoning in order to guide us in these decision making moments?
Where are you????????
Kizzy
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum





