No worries!

Going through section 2 again, I got some details about the elementary form of value wrong - symmetry of the trade relation is baked in from the start. The elementary form of value consists of otherwise unstructured symmetric pairs of pairs, so instead of just being the minimal reflexive relation, it's the minimal reflexive+symmetric relation of trades seen from either side - another feature of it is that the relation is not consistent with a strict ordering on trades. There's also a discussion to be had over whether stipulating that the T relation is reflexive is a harmless embellishment, a decent exegesis or occludes part of Marx's account, which I will do. The expanded form still appears to consist in the transitivity condition and the money commodity still appears to function like the canonical representative of a value equivalence class, though the formal equality of these ideas with Marx's turns on whether it's OK to treat the trade relation as reflexive.

So yeah, there's some work to do - clearing up previous misconceptions and discussing the introduction of orders that respect the value relation and the commutative monoid of commodities. What I wrote previously - especially the bits after the elementary form - I believe is largely fine.

note to self: sum like vs mean like orders in prospect theory

Marx recaps the 'spectral objectivity' of value in commodities and sets up what is at stake in providing a theory of value.

Commodities come into the world in the shape of use values, articles, or goods, such as iron, linen, corn, &c. This is their plain, homely, bodily form. They are, however, commodities, only because they are something two-fold, both objects of utility, and, at the same time, depositories of value. They manifest themselves therefore as commodities, or have the form of commodities, only in so far as they have two forms, a physical or natural form, and a value form.

This paragraph is an elaboration of the idea that commodities are composites of use and exchange value; the elaboration being that exchange value has some formal characteristics apart from the aforementioned relationship with socially necessary labour times. This formal structure of value in commodities is the ground upon which the magnitudes of value make sense...

The reality of the value of commodities differs in this respect from Dame Quickly, that we don’t know “where to have it.” The value of commodities is the very opposite of the coarse materiality of their substance, not an atom of matter enters into its composition. Turn and examine a single commodity, by itself, as we will, yet in so far as it remains an object of value, it seems impossible to grasp it. If, however, we bear in mind that the value of commodities has a purely social reality, and that they acquire this reality only in so far as they are expressions or embodiments of one identical social substance, viz., human labour, it follows as a matter of course, that value can only manifest itself in the social relation of commodity to commodity. In fact we started from exchange value, or the exchange relation of commodities, in order to get at the value that lies hidden behind it. We must now return to this form under which value first appeared to us.

and situates the structural analysis of value, initially, within an account of exchange as the exchange of commodities...

Every one knows, if he knows nothing else, that commodities have a value form common to them all, and presenting a marked contrast with the varied bodily forms of their use values. I mean their money form. Here, however, a task is set us, the performance of which has never yet even been attempted by bourgeois economy, the task of tracing the genesis of this money form, of developing the expression of value implied in the value relation of commodities, from its simplest, almost imperceptible outline, to the dazzling money-form. By doing this we shall, at the same time, solve the riddle presented by money.

which comes to underpin the application of prices to them. Thus...

The simplest value-relation is evidently that of one commodity to some one other commodity of a different kind. Hence the relation between the values of two commodities supplies us with the simplest expression of the value of a single commodity.

we begin with the simplest example of exchange; exchange of one commodity for another.

exchange of one commodity for another. — fdrake

Transfer of property rights? That's how gift economies are described, but there's worry that this is an ethnocentric description.

This is 'old ground' for the thread, but it is presented in a lot more detail (and with one of my misconceptions cleared up).

SUBSECTION A: The Elementary or Accidental Form Of Value

{

Marx's pictogram of this constituent of the value form

x commodity A = y commodity B, or
x commodity A is worth y commodity B.

20 yards of linen = 1 coat, or
20 Yards of linen are worth 1 coat.

}

SUBSUBSECTION 1: The two poles of the expression of value. Relative form and Equivalent form

This part of the account locates two components of the value form; the relative form of value and the equivalent form of value; and exhibits a structural symmetry between them. The equivalent and relative forms of value are a necessary constituent of the form of value. The relative and equivalent form together specify the behaviour of the value form whenever we say that x has the same value as y. Whenever we can say that x has the same value as y; ie whenever the relative and equivalent form are jointly in play; we can say that the elementary form of value is at play too. Additional structure will be applied to the elementary form of value, yielding more constrained (yet algebraically more rich) forms of value.

Note that underpinning this account is the commensurability of commodities under the analysis of socially necessary labour time (and its direct price, a term which has its conceptual origin here, though it is not used explicitly by Marx).

The whole mystery of the form of value lies hidden in this elementary form. Its analysis, therefore, is our real difficulty.

In a similar sense to which the analysis of capital pivots upon the analysis of the commodity, the analysis of the exchange value of that commodity pivots on the understanding of the elementary form of value - which then leads to the exegesis of richer forms of value that can subsume the elementary form.

Here two different kinds of commodities (in our example the linen and the coat), evidently play two different parts. The linen expresses its value in the coat; the coat serves as the material in which that value is expressed. The former plays an active, the latter a passive, part. The value of the linen is represented as relative value, or appears in relative form. The coat officiates as equivalent, or appears in equivalent form.

At this point, I will introduce the relation T. T is a relation on a set of commodities C. Whenever x is related in way T to y, I will write xTy, Formally, a relation on a set X is a set of ordered pairs of objects from X. In this way, T will be a relation on C. Read 'T' as 'is worth the same as', so xTy is read 'x is worth y'.

Marx begins with an example of the linen and the coat; say 2 square yards of linen is worth 1 coat. Then we have, abbreviating, (2 linen)T(1 coat). This is the relative form of value for 2 linen, and 1 coat is serving as the equivalent.

The next paragraph asks the question of whether (2 linen)T(2 linen) gives the value of linen in linen.

The relative form and the equivalent form are two intimately connected, mutually dependent and inseparable elements of the expression of value; but, at the same time, are mutually exclusive, antagonistic extremes – i.e., poles of the same expression. They are allotted respectively to the two different commodities brought into relation by that expression. It is not possible to express the value of linen in linen. 20 yards of linen = 20 yards of linen is no expression of value. On the contrary, such an equation merely says that 20 yards of linen are nothing else than 20 yards of linen, a definite quantity of the use value linen. The value of the linen can therefore be expressed only relatively – i.e., in some other commodity. The relative form of the value of the linen presupposes, therefore, the presence of some other commodity – here the coat – under the form of an equivalent. On the other hand, the commodity that figures as the equivalent cannot at the same time assume the relative form. That second commodity is not the one whose value is expressed. Its function is merely to serve as the material in which the value of the first commodity is expressed.

Marx answers 'no'; "It is not possible to express the value of linen in linen. 20 yards of linen = 20 yards of linen is no expression of value. On the contrary, such an equation merely says that 20 yards of linen are nothing else than 20 yards of linen, a definite quantity of the use value linen.".

It is certainly true that the value of linen will always be the value of linen, irrelevant of what that value is, just as it is true that the value of a coat will always be the value of a coat. Marx suggests that because '2 linen is worth 2 linen' does nothing to express the value of linen relative to anything else, that it cannot be an expression of the relative value of linen; simultaneously, x cannot serve as the equivalent form for x. I grant that this is true; it is completely uninformative about the value of linen to say that it is worth linen.

When two distinct commodities were brought into the exchange relation in section 1, the qualitative particularity of each could not serve as the quantitative measure for both as equal; all concrete particularities of labour were agglomerated into human labour in the abstract. Marx suggests that this account; by which two distinct commodities were exhibited in their equivalence; would not work for the same commodity to exhibit it in equivalence with itself; the commodity is itself in every way. The meeting of a commodity with itself in exchange may be seen as a degenerate, impossible case that undermines Marx's argument of the relation of time and value. See just below to ground this point in the text:

It is not possible to express the value of linen in linen. 20 yards of linen = 20 yards of linen is no expression of value. On the contrary, such an equation merely says that 20 yards of linen are nothing else than 20 yards of linen, a definite quantity of the USE VALUE linen.

My claims:
(1) Marx suggests that this account; by which two distinct commodities were exhibited in their equivalence; would not work for the same commodity to exhibit it in equivalence with itself; the commodity is itself in every way.
(2) the qualitative particularity of each could not serve as the quantitative measure for both as equal; all concrete particularities of labour were agglomerated into human labour in the abstract.

(1) is rooted in the use of 'are', bolded and italicised, in the above quote.
(2) is rooted in the last clause of the bolded sentence, with reference to the 'USE VALUE' of linen which I capitalised. Linen meets itself, so it still meets itself as an amount of a concrete particular.

This comes down to the question of whether T is reflexive; whether for all x: xTx. Perhaps Marx would answer no, but I would like to argue that this additional assumption does no damage Marx's account, and is worthwhile on the basis of its utility in formalising his value theory.

While it is true that linen meeting linen would not allow the derivation of the relationship of human labour in the abstract to value, in terms of the socially necessary labour time of linen, if a meeting of linen with another commodity had already been posited, the concrete particularities of linen as a use value would still be excluded from the relation expressing its value. This is to say, we may say xTx and 'x is the same as x' can mean different things. Specifically, xTy says 'x is worth y'; a numerical equality of something in each in some unit of measure; whereas 'x is the same as y' is a full identity of all properties.

So yes, I am in agreement with Marx on both points; that xTx tells you nothing about the specific value of x, and that xTx could not be analysed in the same way to argue for abstract labour's magnitudinal relation to time. But I believe that if we consider xTx, xTy, yTx and yTy together, we still exhibit the relative form of x in y; in which y is the equivalent (xTy). And the relative form of y in x; in which x is the equivalent (yTx), so in (xTx) and (yTy), the commodities can already be understood not to meet as identical use values, but to meet as numerically identical exchange values. The instances of the relation xTx and yTy are still value uninformative; and this property aligns well with the reflexivity of T. Just as with usual mathematical equality, x=x, we don't immediately derive a conceptual contradiction regarding relative and equivalent forms because x=x for all x, we treat x=x as an uninformative tautology about the value of x.

So from now on, I will assume that T is a reflexive relation, and that this does no damage to Marx's account.

Marx continues:

No doubt, the expression 20 yards of linen = 1 coat, or 20 yards of linen are worth 1 coat, implies the opposite relation. 1 coat = 20 yards of linen, or 1 coat is worth 20 yards of linen. But, in that case, I must reverse the equation, in order to express the value of the coat relatively; and so soon as I do that the linen becomes the equivalent instead of the coat. A single commodity cannot, therefore, simultaneously assume, in the same expression of value, both forms. The very polarity of these forms makes them mutually exclusive.

The two sentences are important for the mathematical structure of T:

No doubt, the expression 20 yards of linen = 1 coat, or 20 yards of linen are worth 1 coat, implies the opposite relation. 1 coat = 20 yards of linen, or 1 coat is worth 20 yards of linen.

This is literally the meaning of the symmetry of a relation: if xTy then yTx. If x is worth y then y is also worth x. This establishes that T is symmetric. It is now reflexive and symmetric. But it is worth lingering a little here to highlight some extra mathematical structure that Marx is aware of.

But, in that case, I must reverse the equation, in order to express the value of the coat relatively; and so soon as I do that the linen becomes the equivalent instead of the coat.

If C = {x,y}, and xTy, then T on y is:

$T=\{ \{x,x\}, \{y,y\}, \{x,y\},\{y,x\}\}$

from symmetry and reflexivity. Look at what happens when we reverse the order in which elements are brought under T, calling this new relation T*

$T^*=\{ \{x,x\}, \{y,y\}, \{y,x\},\{x,y\}\}$

it's exactly the same relation as T, just with the order of the last two pairs flipped. So:

$T=T^*$

those familiar with some order or category theory may notice that T is self dual. This means it is the same as before when the order of all pairs is flipped. Writing this out in words might make the (for me, squee inducing) conclusion clearer:

T is: (1) x is worth x
(2) y is worth y
(3) x is worth y (x relative, y equivalent)
(4) y is worth x (y relative, x equivalent)

T* is: (1) x is worth x
(2) y is worth y
(3) y is worth x (y relative, x equivalent)
(4) x is worth y (x relative, y equivalent)

the part of the relation dealing with the relative and equivalent forms of value inverse their order when the order of the pairs are reversed. This means that the notion of relative form is dual to the equivalent form in the category theoretic sense, and the relation of values T is self dual as a consequence of that (and of symmetry).

Whether, then, a commodity assumes the relative form, or the opposite equivalent form, depends entirely upon its accidental position in the expression of value – that is, upon whether it is the commodity whose value is being expressed or the commodity in which value is being expressed.

And it seems Marx was aware of this duality of structures - assuming the relative or equivalent form are just positional accidents which imply the other accident. The structure Marx diagnoses of the elementary form of value is unperturbed by the assumption of the reflexivity of the 'is worth' relation.

The role property rights play in capital comes later. Just before the dolphins.

Ok. But nobody would trade 20 yds of linen for 20 yds of linen (if the bolts were identical.)

Yes.

What would the exchange relations look like in a mode of production that satisfied the elementary form of value? This breaks down into two questions:

(1) What would the exchange relations look like in a mode of production that satisfied the elementary form of value alone with no additional constraints?
(2) If (1) does not look like the capitalist mode of production, what additional constraints are required to more accurately model the form of value in capitalist production?

The logical space of exchange relations which satisfy (1) is very broad, and does not even need to have a stable numerical equivalence of values over repeated exchanges. This can be shown thusly:

If we have 4 commodities, x=1 coat, y= 1 pair of trousers, z=1 yards of linen,2z=2 yards of linen. Assume they trade concretely like:
(1) 1 coat is worth 1 pair of trousers|xTy
(2) 1 pair of trousers is worth 1 yard of linen|yTz
(3) 2 yards of linen is worth 1 coat|2zTx

then make it satisfy the symmetry condition (flipping the relations around):

(4) 1 pair of trousers is worth 1 coat| yTx
(5) 1 yard of linen is worth 1 pair of trousers| zTy
(6) 1 coat is worth 2 yards of linen| xT2z

Say I start with z = 1 yard of linen.

z->y->x->2z is a possible sequence of trades, using zTy, yTx, xT2z. This means we could start with 1 yard of linen and end up with 2 despite only going through trades of equivalent value. To be able to say that 1 yard of linen is worth 2 yards of linen through the medium of exchange should tell us that something is very different from how exchange works under capitalist production. IE that the elementary form of value alone and without additional constraints is not a good picture of how value works in capitalist societies, at least most of the time.

It is within the potential of the elementary form of value to amplify (or diminish) the value owned through trade of things held equivalent, which is to say that considerations of value magnitude are only done relationally through T and not through an equation of numerical magnitudes of the same unit. The ability to alter held values in this manner is unlikely to survive in a stable community which has common knowledge of how much of one thing trades for another. Thus the situations this raw elementary form of value could hold sway in are those that have sufficiently rapid fluctuations in the relative values of commodities (fluctuations more rapid than the actions of trade) or when some part of the system of exchanges occurs isolated from another.

Another thing to note is that the elementary form of value doesn't need to have anything which resembles money in any way; all commodities are as good as any other as the repositories of value. Under the conditions above, if there were a common currency for the system of exchange it could literally be used to buy more of itself through a series of favourable trades, supposedly of equal 'value'.

Such a mitosis of money has precedents in the real world. However, the mitosis in reality leverages temporal instabilities in the trade relation - which are juxtaposed without temporal indices in the elementary form. The elementary form above should hence be thought of as the elementary form at a given time and place because the determination of its features depends more on accidental irregularity than essential regularities.

I think there's some additional work that needs to be done at this point, the details could be glossed over and you could understand Marx's value theory regardless, but because I'm trying to take an algebraic approach to Marx's value theory when a mathematical problem presents itself I have to address it.

Given the elementary form of value, it makes sense to ask questions like "if 1 coat trades for 1 pair of trousers, and if 2 yards of linen trade for 1 suit jacket, if I have 1 coat and 2 yards of linen can I trade both for 1 pair of trousers and a suit jacket?'. The question here is whether there is any algebraic structure to the set of possible trades involving multiple goods.

My account has changed a little, the basic ideas were right but I flubbed some of the detail. In order to make sense of multi-commodity trades, let's look at the difference between buying beef mince from a butcher in a specific weight (called BM), and buying beef mince from a supermarket in a wrapped packet (called SM).

If I was writing a shopping list, the only possible amounts of SM which could be obtained are non-negative integer multiples. This is to say that I could buy 1 packet, 2 packets, 3 packets and so on, or indeed 0 packets and buy none. SM comes in discrete amounts.

Whereas, on the same shopping list, I could buy non-discrete amounts of BM. 50 grams, 53.1 grams, 100 grams, 1.23456kg and so on. GM comes in amounts which are infinitely divisible.

I think these properties exhaust the possible amounts commodities could be bought in: either you have a discrete amount or you have an infinitely divisible amount (in principle but not in practice). If it turned out that there was a smallest denomination of every given commodity of which every possible amount was a multiple, the discrete amounts alone would suffice. But I don't think it's fair to make this assumption given that things like meat can be bought in approximated fractions of any given amount.

I will call the collection of amounts which a commodity can come in the amount-structure of a commodity. Just like a shopping list, it's required to be able to write down any amount possible of the commodity, but also to be able to add on or scale the amount by a number to adjust for different recipes or different numbers of people eating and so on.

Commodities like SM which come in discrete units I will call discrete commodities, commodities like BM which come in approximated infinitely divisible amounts I will call continuous commodities. I'll now discuss the amount-structure of SM.

If I buy an SM, then buy another SM, this is the same as buying 2 SM. Similarly, if I wanted to buy 1 SM but needed to scale up for more company, I could buy 2*1SM and get 2 SM. This says that the amount-structure of discrete commodities, henceforth called the discrete amount structure, has two mathematical operations contained in it which interact: addition of other amounts of SM, and multiplication of all amounts present by some non-negative integer. This means that dealing with SM is exactly the same as dealing with the non-negative integers under addition and multiplication. Such additions and multiplications obey the distributive law c*(a+b)SM = ca + cb SM and are commutative and associative. There can be no subtraction or division of amounts, since -1SM and 0.5SM are not possible numbers of commodities to buy (respectively). There are two identities, if I multiply an amount by 1, it remains the same., similarly if I add a 0 amount. So the discrete amount structure for a single commodity is a commutative semiring with multiplicative (1) and additive (0) identity elements.. It also needs to be assumed that SM = 1 SM, which is essentially a notational convenience.

If I buy a weight X of BM, then I could scale it up by 1.5 and still have a buyable amount of BM, 1.5X BM. I could also divide X by 2 and have a buyable amount, 0.5X BM. I could double then halve the amount of BM and receive the original amount. I still cannot buy -1 BM however. Addition and multiplication also follow the distributive law together. These together mean that the continuous amount structure has a commutative semigroup with identity (0) as its additive component, and a commutative group (with identity 1 and multiplicative inverses) when ignoring 0 (which has no multiplicative inverse).

The last thing which needs to be clarified before proceeding is what it means to write down, say, 1 coat + 1 pair of trousers; to demarcate the possible combinations of the commodities. For a set of commodities with the same amount structure, defining the set C of commodities present in their canonical amounts (like 1 SM 2 paragraphs above) and equipping it with free addition - writing symbols side by side with a plus between - suffices. This can be thought of as writing down two items on a shopping list from the possible things which can be bought from the store. It is also the case that the order things are written down don't matter. This makes (as before) the set C the commutative free semigroup under addition.

These observations give the tools to go a little further. What if in addition to SM I would like to buy a coat? Well, the amount structures are the same, so I could say I will buy 1 SM + 1 coat, where + is understood as agglomerating the objects into a shopping list. I could add any amount of coats or an amount of SM and still obtain a viable shopping list of goods. If I wanted to double the amount of coats and triple the amount of SM I could do that too. So what should be formalised is essentially many labelled copies of the same amount structure occurring side by side without influencing each other (eg, ruling out things like 1SM + 2 coats = 3SM). The appropriate definition then is very much like a module over a ring, but since there aren't additive inverses for the discrete amount structure it can't be a ring. Regardless, it will follow some of the same rules:

We have a set of discrete commodities DC, each of which has the same amount structure M (the non-negative integers). The addition and multiplication, from the previous discussion, follow the laws:

(A) r*(x+y)=r*x+r*y, for all r in DC and x,y non-negative integers
(B) (r+s)*x=r*x+s*x, for all r,s in DC and x non-negative integers

(A) formalises that adding the amounts before you buy them to obtain the intended amount is the same as buying distinct amounts which sum to the intended amount.
EG: SM*( 1 + 2 ) = 1 SM + 2 SM
(B) formalises that you can scale your entire shopping list up by any non-negative integer and this is the same as buying that multiple of each item.
EG: (SM + coat)*2 = 2*SM + 2*coat

This structure will be called (DC,+,*).

An analogous argument holds for the continuous amount structure on the set CC and it also satisfies A and B but with x,y rational or real. That structure will be called (CC,+,*). This allows the aggregation of arbitrarily many discrete and arbitrarily many continuous commodities, but does not solve the riddle of their interaction; the structure of writing down 1 SM + 0.5 BM still needs to be fleshed out.

If it helps, writing down examples for the continuous and discrete cases individually looks exactly the same as doing calculations with vectors; if there are N distinct discrete commodities in the expression, the amounts of each will be written in front of each commodity. Additions work component-wise. Similarly for the continuous commodities.

The analogy with vector spaces suggests that sandwiching the structures DC and CC together in parallel, like the dimensions of vectors are sandwiched together, is an appropriate strategy. This means that continuous commodities will never add to discrete commodities and start mucking up the appropriate amounts which can be bought. The thing I'm aiming at is a closed mathematical structure that allows addition and multiplication in the right way. To be sure, multiplication by a scalar is more involved than with vector spaces because things like 0.5 coats make no sense. This means scalar multiplication also needs to be somehow partitioned to act on discrete and continuous commodities separately; or alternatively removed entirely as it cannot act on discrete and continuous commodities at the same time for non-integer scalars.

A tentative guess I have for this structure is to take (DC,+,*) and (CC,+,*) as generators for the overall structure of commodity amounts, and simply define that structure as the collection of formal sums of arbitrary elements in DC with CC, and to define addition as 'component-wise' addition in DC and CC respectively - and just leave overall scalar multiplication undefined. To be sure, this would allow the production of lines like:

0.5BM + 2CM+BM+CM= 1.5BM+3SM

and like calculations. Addition and multiplication of the whole thing by non-negative integers (the discrete amount structure) can be easily defined too since the addition in both is commutative; ie the semigroup action construction, 2SM = SM+SM from before, but now 2*(1.5BM)=1.5BM+1.5BM=3BM too. I suppose that will have to do.

If I call the set of commodities C whose components are generated by (DC,+,*) and (CC,+,*) then glued together through + (C,+), this facilitates setting up the elementary form of value on C. It works essentially the same as I discussed before but with a few minor alterations:

(1)batches of commodities can be compared to batches of commodities.
(2) if two expressions in (C,+) evaluate equally then they should be treated the same. This is to say that, say, 2SM+1BM=2*(SM+0.5BM) and so 2SM+1BM is worth 2*(SM+0.5BM) and vice versa.

This means, unfortunately, that an equivalence relation should be defined on (C,+) - so that sentences in (C,+) which evaluate equally are substitutable for each other. EG since 2SM + 1BM is the same as 2*(SM+0.5BM), if (2SM+1BM) T (1 coat), then ( 2*(SM+0.5BM) ) T (1 coat). This is so that T respects equality in (C,+). So, formally, T becomes defined on equivalence classes of (C,+) under the relation of equality of expressions. Just like I referenced before with the fractions - different ways of writing down the same thing should be treated the same. And also just like with the fractions, this mathematical detail can largely be forgotten since we know how to substitute anyway.

One last note before continuing on with the section on the relative form of value. As I showed before, the elementary form of value by itself can allow 1 coat to be exchanged for 2 coats; so any notion of ordering in terms of commodity amounts isn't compatible with this form of value, and if for some specific realisation of the elementary form it is consistent with such an ordering, it is so by logical coincidence. But there is a real incentive for a social organisation to constrain the value form more; so that trades of equivalent worth don't allow the alteration of value (instantaneously).

Marx seeks to ask a deeper set of questions; what is it about an economy that allows everything to have a price? What is it about an economy that is facilitated by money? How does money obtain its value? — fdrake

I've only made it to the end of the 3rd page in the thread so far, but this is a really nice way of putting it. What immediately stood out for me is that this question is essentially a transcendental one: about the conditions of possibility of price(ing). There's a Kantianism here that's not often acknowledged.

I'm stealing vocabulary from as many places as I need to try and convey the ideas. So yeah, I borrowed conditions of the possibility for that bit. The really interesting thing about that space of questions, methodologically at least, is that the condition for the possibility isn't 'condition for the possibility of conception' alone, it's also 'condition for the possibility of working as is'. I view these kind of questions as providing something like synthetic a-priori knowledge of social structures, but Marx always ends up reading the a-priori structure back into the phenomena to... I don't know, something like 'see things in their motion'. Like collapsing the most developed value form into the money commodity so he can look at circulation of commodities.

There's a real metaphysical thoroughness in his ideas, and a lot of... alchemy of ontological strata.

Mixing metaphors, I think Marx is really sensitive to how the material processes carry along/are driven by the abstractions. To me it feels like the kind of thing Heidegger should've done more, looking at how a body Daseins. Re-inscribing the transcendental in the material, or something like that.

After a few days of trial and error and searching I found a paper that deals with remaining part of the algebraic structure of commodities above - specifically defining a sense of subtraction. So things like (1.5SM + 0.5BM)-(1.3SM + 0.1BM)=0.2SM + 0.4BM make sense.

One of the reasons this was difficult is because if you allow subtraction in usual sense of additive inverse, you 'zero out' the whole structure. Ideally what's needed is some way of allowing calculations like the above, but dealing with things like (1.5 SM) - (1.6 SM) = ? in a manner which keeps the structure closed. If you have 0-x=0 for all x, then add x to both sides, then x=0... So the whole thing is zero.

Another reason this doesn't work in the naive way is: say we have x lots of SM, and want to subtract off (x+1) lots of SM - x and x+1 are both positive amounts of stuff so they are valid elements of the structure.

This gives (x) - (x-1)=0, but by associativity and -ve*-ve=+ve, x-(x-1) = (x-x)+1=1, so 1=0. This is a contradiction.

The right strategy for defining it is to define subtraction (-) as (in principle) an independent operation of addition, then model the links between them in the structure (C,+,*,-) afterwards.

So I (think I) ironed out the difficulties with subtraction and a primitive ordering on C. The following axioms describe the structure, consider first for a single commodity - say $C_i$, with amount structure $D_i$.

Additive component, operation denoted +:
$\text{A1: } x+y=y+x\\\text{A2: }x+(y+z)=(x+y)+z\\\text{A3: } \exists 0\in D: \forall x: x+0=0+x=x$
Multiplicative component, operation denoted .:
$(M1): x.y=y.x\\(M2): x.(y.z)=(x.y).z\\(M3) \text{There is } 1\in D: \forall x: 1.x=x.1=x$
Subtractive component, operation denoted -;
$(S1):(x-y)-z=(x-z)-y\\(S2):\exists 0\in D: \forall x; x-x=0\\(S3):x-0=x\\(S4): 0-x=0$
Additive's interaction with multiplicative:
$(AM1):a.(x+y)=a.x+a.y$
Additive's interaction with subtractive:
$(AS1):x+(y-z)=(x+y)-z\\(AS2):x-(y+z)=(x-y)-z$

It can be seen that the subtractive 0 interacts with multiplication in the following way:
0.a=(a-a).a=a.a-a.a=0
and the additive 0 and the subtractive 0 are equal, 0S is subtractive 0:
x+0S=x+(x-x)=(x-x)+x=0S+x
since 0S satisfies (A3) 0S is also the additive 0.

I'll call this total structure $(D_i,+,-,.)$ the algebraic structure of $C_i$. This iterates over all discrete commodities in C. Grouping together all commodities with a discrete amount structure D, the algebraic structures are then all $(D,+,-,.)$. This facilitates the definition of a module like structure of C over D which satisfies the following axioms, for r,s,t in C and a,b,c,x,y in D:

$(N1): r+(s+t)=(r+s)+t\\(N2): a.(r+s)=ar+as=as+ar=(s+r).a=\\(N3): ar+(bs+ct)=(ar+bs)+ct\\(N4): ar+br=(a+b)r=(b+a)r=br+ar\\(N5): (ar+bs)-(xr+ys)=(a-x)r+(b-y)s$

this list is probably incomplete, but it shows how all the operations interact. Regardless, all it is saying is that (combinations of) operations on commodities, like 2*(1BM+0.5SM)-(1BM+0.5SM), are to be resolved in terms of the pre-established algebra (A1->AS2) on the components, like (2-1)BM+(1-0.5)SM, irrelevant of how many components there are. And also that it doesn't matter what order components (like SM and BM) are written down. Note however that multiplication of commodities is not defined.

All the commodities with the discrete amount structure have the same behaviour of coefficients. All the commodities with the continuous amount structure have the same behaviour of coefficients. Formally, the procedure above should be done again for the continuous amount structure, but it's essentially the same. The only thing which changes is that the multiplicative part without 0 has inverses.

The final construction, being able to deal with lists of commodities with different amount structures, is obtained by gluing the aggregated discrete one above to the one with minor modifications for continuous commodities. Conceptually it looks like this:



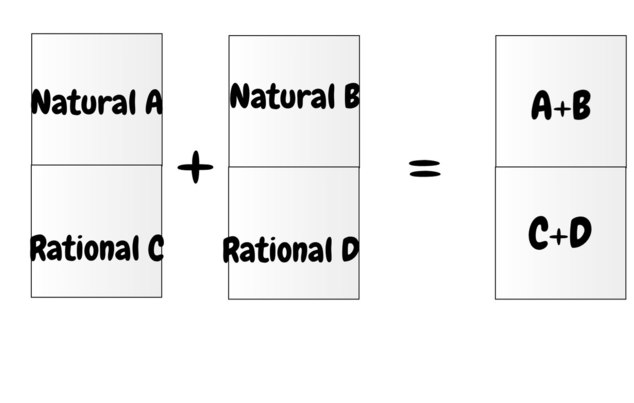
it's just a vector space with different algebras on each component (no longer coefficients from a field).

The last thing to note here is that the subtraction operator allows an order to be defined on the structure of commodities. We can say that 1 list of commodities is greater than another when the second is equal to the first minus some amount of each commodity. So A>=B <=> B-A=0. It inherits this order from each algebraic structure $D_i$ and holds when the inequality holds for all coefficients. So this lets us say things like (1BM+0.5SM)>(1BM+0.25SM). Note, however, that this 'order on the amount of stuff' does not necessarily respect the elementary form of value insofar as 'strictly more goods' can be traded for 'strictly less' and vice versa (go from 2z->z instead here through the trade network).

So to go back to the question which spurred all the algebra:

Does this hold:
If
(1) 1 coat is worth 1 pair of trousers
(2) 1 yard of linen is worth 1 suit jacket
then
(3) 1 coat + 1 yard of linen is worth 1 pair of trousers + 1 suit jacket

and what happens if it does hold?

When it holds, and always holds, you end up with the following implication on T:

Addition:
If:
(A) xTy and aTb
then
(B) (x+a)T(y+b)

If you augment this with the multiplication and subtraction structures you also get:

Multiplication:
If
(C) xTy
then
(D) (a)xT(a)y (where a is an element consistent with the amount structure of x and y)

(1 coat is worth 1 pair of trousers <=> 2 coats are worth 2 pairs of trousers)

Subtraction:
If
(E) xTy
then
(F) (x-a)T(y-a)

this lets the algebraic structure above interact with the relation in a sensible way. It also will lead to a characterisation result later when we bring in the mapping to values (probably). Observe that the thing which violated the intuition of preserving value through trade above was that we could trade 1 yard of linen for 2 yards of linen above. If we could obtain 1 yard of linen and 1 coat for 1 yard of linen, this would be precisely the same violation conceptually and differ only in the accounting. So we have that:

"T preserves numerical equality of value"
iff
For no commodities a,b aT(a+b).
iff
0Tb (subtract a from both sides and use the commutativity of addition to rearrange the right side to b+a, then (b+a)-a=b+(a-a)=b+0=b.

which is quite nice - the elementary form 'preserves the numerical equality of value' if and only if 'you can't trade something for nothing'. To me that's quite convincing that I'm on the right track.

edit: Preserving the numerical equality of value can also be stated in terms of the ordering on C through subtraction. "T preserves the numerical equality of value" iff "for no a,b such that b>a aTb", and this is equivalent to the above equivalences. This is because b>=a iff a-b=0 (remember the subtraction axiom S4).

Moving onto the next section:

Subsection 2: The relative form of value.
Subsubsection (a): (a.) The nature and import of this form

The overall thrust of this section is to provide a deeper description of the relative form of value referenced in the previous section. Marx deals with how definite quantities of use values can be considered equal in value, then considers various quantitative operations on the relative value of commodities and how they work in the relative form of value.

In order to discover how the elementary expression of the value of a commodity lies hidden in the value relation of two commodities, we must, in the first place, consider the latter entirely apart from its quantitative aspect. The usual mode of procedure is generally the reverse, and in the value relation nothing is seen but the proportion between definite quantities of two different sorts of commodities that are considered equal to each other. It is apt to be forgotten that the magnitudes of different things can be compared quantitatively, only when those magnitudes are expressed in terms of the same unit. It is only as expressions of such a unit that they are of the same denomination, and therefore commensurable.

Marx begins; if we were to consider that 1 coat is worth 1 pair of trousers, what is it that allows the equation of the two commodities? Marx spurns the idea that the number of coats and the number of trousers suffices for an explanation of their equivalence in value because these numbers are dimensionless. The equation 1 = 1 in terms of 'coat units' and 'trouser units' tells us nothing about what about 1 coat and what about 1 pair of trousers renders them of equivalent worth. The comparison of raw quantities of coats and trousers requires a common unit under which the two are indeed comparable before can can be deemed equivalent.

A common example of this is the claim that "1+1=2". This is usually (and rightly) understood as the natural number 1 plus the natural number 1 is numerically equal to the natural number 2. However "1+1=2" can be false depending on the context. If these numbers corresponded to measurements on the decibel scale, 1dB+1dB=4dB, so "1+1=4" in this context. Thus, the context of the numbers must be understood in order to do these calculations. If our context is that of the dimensionless naturals, 1+1=2, if our context is that of the decibel scale, 1+1=4. The commensurability of numbers depends on their scale (or their joint absence of a scale).

The common unit under which 1 coat and 1 trousers can be seen as equivalent is that of either time or the monetary expression of time; socially necessary labour time or direct price. Note that if we already contextualise 1 coat = 1 pair of trousers in terms of real price, we can say that 1 coat 'is the same price as' 1 pair of trousers, but this does not provide an account of why they are commensurable in terms of prices in the first place. Marx summarises it like this:

Whether 20 yards of linen = 1 coat or = 20 coats or = x coats – that is, whether a given quantity of linen is worth few or many coats, every such statement implies that the linen and coats, as magnitudes of value, are expressions of the same unit, things of the same kind. Linen = coat is the basis of the equation.

and proceeds to give a clever example of the contextual basis of equality of quantities:

But the two commodities whose identity of quality is thus assumed, do not play the same part. It is only the value of the linen that is expressed. And how? By its reference to the coat as its equivalent, as something that can be exchanged for it. In this relation the coat is the mode of existence of value, is value embodied, for only as such is it the same as the linen. On the other hand, the linen’s own value comes to the front, receives independent expression, for it is only as being value that it is comparable with the coat as a thing of equal value, or exchangeable with the coat. To borrow an illustration from chemistry, butyric acid is a different substance from propyl formate. Yet both are made up of the same chemical substances, carbon (C), hydrogen (H), and oxygen (O), and that, too, in like proportions – namely, C4H8O2. If now we equate butyric acid to propyl formate, then, in the first place, propyl formate would be, in this relation, merely a form of existence of C4H8O2; and in the second place, we should be stating that butyric acid also consists of C4H8O2. Therefore, by thus equating the two substances, expression would be given to their chemical composition, while their different physical forms would be neglected.

To clear this up, if 'x is worth y', then x is playing the part of the relative form, and y is playing the part of the equivalent form. This means 'x is worth y' is a statement which expresses the value of x in terms of y. So when Marx says:

But the two commodities whose identity of quality is thus assumed, do not play the same part. It is only the value of the linen that is expressed. And how? By its reference to the coat as its equivalent, as something that can be exchanged for it. In this relation the coat is the mode of existence of value, is value embodied, for only as such is it the same as the linen. On the other hand, the linen’s own value comes to the front, receives independent expression, for it is only as being value that it is comparable with the coat as a thing of equal value, or exchangeable with the coat.

"It is only the value of linen that is expressed", he is restating that linen in the equation of x linen = y coats is in its relative form. There is a little subtlety in the account here; Marx is putting in a lot of effort to exhibit an asymmetry between the relative and equivalent form, nevertheless x is worth y implies y is worth x, so what's the point of this pedantry?

Underlying the numerical equality of "x coats is worth y pairs of trousers" is a sortal determination of equality; the origin of 'commensurability' of coats and linen. "x coats' has to be able to count as "y pairs of trousers" in order for the equation "x coats = y pairs of trousers" to hold. This counts as is echoed by the requirement that x coats and y pair of trousers share a common unit in which the two are equivalent, and the 'counts as' must be able to be applied to 'x coats' and 'y pairs of trousers' individually as they are just examples of the 'is worth' relation which takes two things which can count as each other in determinate quantities of labour; as units with the same magnitude on the same scale. And just as before with the notion of shapes as equivalent under the equality of areas, whatever makes x coats worth y pairs of trousers must be a property of both coats and trousers which has a magnitude. Because the example was arbitrary, the sortal which renders coats equivalent to trousers; as commensurable quantities, as numerical values; has to exceed both items in its capacity for application.

Another feature of this sortal application is that it filters out properties which are not relevant for the sortal: in Marx's example, two substances have the same chemical formula but different molecular geometries; we can say they are equal in terms of chemical formula to the extent we ignore the properties irrelevant to the sortal of chemical formulae on compounds, atoms and molecules.

Marx continues, drawing out this connection between the ability for commodities to count as each other and as their equivalence under the sortal 'are congelations of human labour in the abstract. The paragraph is quite dense, so I'll spend some time charting it.

If we say that, as values, commodities are mere congelations of human labour, we reduce them by our analysis, it is true, to the abstraction, value; but we ascribe to this value no form apart from their bodily form. It is otherwise in the value relation of one commodity to another. Here, the one stands forth in its character of value by reason of its relation to the other.

Under the aspect of value, commodities are nothing but human labour embodied in goods. But this is an abstraction; an insubstantial relation between goods. Dissecting the goods will not reveal an atom of value, nevertheless the value persists in them to the extent they partake in the structure of value. Marx sees it as important to highlight that 'this value has no form apart from (the commodities) bodily form'. Value is immaterial, but it nevertheless partially constitutes every commodity. This harkens back to my first post detailing the nature of real abstractions. Commodities should be understood as real abstractions; dynamic, interlinking corpuscles which partake in multiple ontological registers.

In terms of the value relation, only the relative value of commodities is revealed - only the value form operates on commodities; under other aspects (such as the satisfaction of wants or needs), other aspects like specific use values emerge. It is prescient to note that this insistence on the non-bodily nature of value comes right after an example with a similar structure; of the equation of chemicals under the aspect of chemical formulae. The chemical formula is 'in' the chemicals in precisely the same sense that value is 'in' commodities. The analysis of the value form is the analysis of the logical structure of value in commodities, but also an analysis of how that form inheres in the material structure of commodities. Ultimately, this comes down to material structures counting as value alone under certain social processes; like purchase, exchange, investment and so on.

By making the coat the equivalent of the linen, we equate the labour embodied in the former to that in the latter. Now, it is true that the tailoring, which makes the coat, is concrete labour of a different sort from the weaving which makes the linen. But the act of equating it to the weaving, reduces the tailoring to that which is really equal in the two kinds of labour, to their common character of human labour. In this roundabout way, then, the fact is expressed, that weaving also, in so far as it weaves value, has nothing to distinguish it from tailoring, and, consequently, is abstract human labour. It is the expression of equivalence between different sorts of commodities that alone brings into relief the specific character of value-creating labour, and this it does by actually reducing the different varieties of labour embodied in the different kinds of commodities to their common quality of human labour in the abstract.

Marx restates himself, the equation of commodities with different production processes under the equality of value deforms human labour to value creating labour; that is, abstract (social) labour. All labours are the same in terms of value creation. This references the homogeneity of human labour in the abstract as previously discussed, and so is mostly old ground. The only new thing here is rephrasing 'human labour in the abstract' as 'value creating labour'.

But, there is another subtlety, Marx makes a claim about the reality of this value form in exchange.

It is the expression of equivalence between different sorts of commodities that alone brings into relief the specific character of value-creating labour, and this it does by actually reducing the different varieties of labour embodied in the different kinds of commodities to their common quality of human labour in the abstract.[

While it is possible in the realm of intellectual abstractions to reduce commodities to the general features of labour embodied in them, Marx claims that such a reduction isn't simply one performed by an intellectual in an armchair, he claims that the reduction of concrete labour to abstract labour really does occur as part of the process of valuation. Whenever we take two commodities as equivalent in value, the equivalence is not just a numerical equivalence, it is the social circumstances which render those commodities as commensurable and equivalent. Ultimately, this comes back to the nature of capital; of the production of commodities for exchange rather than use. The 'perspective' of capital sees commodities as opportunities for profit already, so this reduction to values alone has 'always-already' occurred. It's an a-priori structure of value which is reproduced socially through the production of items for their values rather than their use values. Society already sacrifices utility on the altar of profit.

The 'perspective' of capital sees commodities as opportunities for profit already, so this reduction to values alone has 'always-already' occurred. It's an a-priori structure of value which is reproduced socially through the production of items for their values rather than their use values. Society already sacrifices utility on the altar of profit. — fdrake

So Marx' solution is to have the state own property so that values return to use value rather than profit value?

I am not inherently against or for an economic system, as I fear all work is bad in the first place- whether for an abstract "state" or for a company. But I do find it prima facie kinda scary that in a capitalist system, workers must reenact a sort of medieval structure whereby they must find a lord to dispense a wage/salary and work their "land" (i.e. perform labor for them). Employers have tremendous power over the peasants' lives. Interestingly, there was a podcast episode with Elisabeth Anderson on The Partially Examined Life who claims that owners represent a private government and essentially should have the same restrictions as governments.

The bigger question of how work should be distributed and organized will probably never really be solved being that the demand forces the supply, and thus work. Marx already makes the fatal flaw that "some" form of work is good- that being "unalienated work", which I do not subscribe to. No work is necessarily good in and of itself, it is simply necessary to survive. Exploitation of worker value is no good, but it's not like the work itself, unhindered from this is some sort of salvation from the problem of work itself. It is still work after all.

So Marx' solution is to have the state own property so that values return to use value rather than profit value? — schopenhauer1

I don't think Marx had a solution, or viewed any one social movement or intervention as sufficient for the removal of capitalism. He took a very pragmatic approach in his letters and support of political movements of his time. Regardless, you can see a few things which make social tensions appear in his analysis of capital.

The only ones we've covered so far are the distinctions between value and price, and the distinction between use and exchange values. Values coming untethered from prices makes room for all kind of pathologies (most of which we haven't met yet in the book). The distinction between use and exchange value means that production typically isn't for the social good or the good of the commons; or even to provide a commons; it's to make more money. When capital goes out of its way to satisfy a common need purely to satisfy it it's either an affectation like charity or a concession to an organised group.

Marx's works on labour and species-being are complementary to this. We'll see alienation later if I get to it. :)

I don't mean to downplay the power of volunteer and not-for-profit work to make commons, just to say they remain relatively disempowered despite their universal appeal due to being... not-for-profit organisations.

I don't think Marx had a solution, or viewed any one social movement or intervention as sufficient for the removal of capitalism. — fdrake

So what do you think was his goal in his works? What does a better society for Marx look like? Also, this doesn't get rid of the actual problem which is that work itself might not be a good, but rather something we must deal with to survive. Our demands will always force there to be more supplies, and people are enslaved to their own needs and wants.

So what do you think was his goal in his works? What does a better society for Marx look like? — schopenhauer1

He is notoriously silent on the matter. Perhaps he thought that the people who bring about communism should decide what it looks like. Clearly he approved of measures which make socialism and communism more likely, and clearly wanted production to be tailored for need, desire and communal access rather than profit and privation. He also definitely wanted workers to harness the increased productivity from automation to direct it for the benefit of all.

and clearly wanted production to be tailored for need, desire and communal access rather than profit and privation — fdrake

And what of the tropes that market economies bring about more efficient avenues for increased productivity?

Ask the giant face frying hole in the sky or the Cheetos packets in the Marianna trench, or the deforested areas expanding the floodplains, people who can't afford a cup from the Starbucks on their factory dormitory's street while working 14 hours a day, militias being bribed to kill Coca Cola unionisers, more empty homes than homeless, enough wealth to end world poverty overnight if redistributed... Ask all of those problems what they think about the efficiency of the market in satisfying the needs of humanity.

Granted, yet states with command economies run far short as well- think Eastern Europe by the 1980s. The problem is focus on productivity doesn't necessarily resolve a lot of human-based needs like wanting decision-making power, ownership of one's own labor, not being at the whim of what boss will be the kindest. Work days that are flexible, etc. etc. But again, the problem is work itself. Marx probably saw it as an end in itself if in what he considered its "unalienated form". I do not see it as an end in itself. It is a burden that we put on each other based on our needs and wants. It bothers me someone would need to be "born" so they can "experience" the "intrinsic goodness" of work, whether "unalienated" or not. The problem is our very needs that we have in the first place. It is a metaphysical problem that is not answered via economic system changes.

Life might not be worth living, but it could still be better.

Also don't forget, more productivity and markets brings more variety. People generally forgo a lot of stuff for just the right pair of such and such.